Abwurfgeschwindigkeiten berechnen

bbcinek89 · Anmeldungsdatum: 03.10.2010 Beiträge: 16

Hallo, ich lerne gerade Physik aber diese Aufgabe überforert mich.

Von einem Turm mit der Höhe = 40m werden zwei kugeln gleichzeitig abgeworfen: Kugel 1 wird unter dem Neigungswinkel 30° zur Horizontalen schräg nach oben abgeworfen, Kugel 2 wird senkrecht nach oben geworfen. Die Kugel 1 schlägt 95m entfernt vom Fußpunkt des Turmes auf; die Kugel 2 unmittelbar am Fußpunkt, aber t=1,2 s später als die Kugel 1. Berechnen Sie die Abwurfgeschwindigkeiten der Kugeln.

Formel senkrechter Wurf nach oben
Wurfhöhe h(t) = v0*t-1/2g*t²
Geschwindigkeit
v(t) = v0 - g * t
v(h) = -+ Wurzel v0² - 2*g*h

normal wär es ja eine Formel nehmen und nach v0 umstellen

aber ich habe bei der ersten und zweiten Formel zwei umbekannte v0 und t und bei der dritten habe auch zwei unbekannte aber v0 und h also kann ich damit nicht arbeiten.

Mehrdimensionale Bewegung: schiefer Wurf

Weg s(t) = (x= v0*t*cos(b) y= v0*t*sin(b) - g/2 t²)
Geschwindigkeit s(t) = v(t) = (x=v0*cos(b) y= v0*sin(b)-g*t)
Wurfparabel y(x) = x tan(b) - g/(2v0²*cos²(b)) * x²

Hier das gleiche: Alle Formeln haben zwei unbekannte v0 und t

Also wie muss ich da ran gehen?

fuss · Anmeldungsdatum: 25.05.2010 Beiträge: 519

betrachte zunächst mal den schrägen Wurf, weil du da am meisten gegeben hast.
Du hast gegeben:Abwurfwinkel, Abwurfhöhe (und damit Aufschlaghöhe auf dem Boden vom Abwurfpunkt aus gesehen) und Wurfweite.
Nun leitest du dir die Bewegungsgleichungen für den schrägen Wurf her bzw. da du einige hier schon hingeschrieben hast, wende sie auf dieses Problem an.

Jetzt hast du ein paar Daten für die schräg geworfene Kugel gewonnen und kannst damit dann weiterrechnen für Aussagen über die senkrecht hochgeworfene Kugel.

bbcinek89 · Anmeldungsdatum: 03.10.2010 Beiträge: 16

aber abwurfhöhe und wurfweite kommen aber in keiner der formel vor. wie soll ich dann die werte die ich zwar habe dann einbauen?

fuss · Anmeldungsdatum: 25.05.2010 Beiträge: 519

Du kannst das auch ohne fertige Formel genau so gut unter Zerlegung des schrägen Wurfes herleiten, indem du z.B. auch erst mal nur die Bewegung bis Höhe 40 m betrachtest, also wie einen "normalen" schrägen Wurf, wo der Körper auf der Höhe wieder aufkommt, wo er abgewurfen wurde.
Weißt du, wie man bei einem "normalen" schrägen Wurf Eigenschaften wie Wurfweite, Wurfhöhe, Wurfzeit bestimmt? (Man muss dazu die Geschwindigkeit in y-und x-Komponente zerlegen, also senkrechte und waagerechte Komponente, und kann dann u.a. über die Symmetrie der Wurfparabel Aussagen darüber machen, wie lange die Zeit bis zum höchsten Punkt ist, welche Strecke da in y- und x- Richtung zurückgelegt wurde etc.).
Ich würde dir empfehlen, dir das noch mal genau anzuschauen, weil das Verständnis der Gleichungen ist die Grundlage fürs Rechnen.

Anschließend betrachtest du den Rest der Bewegung, quasi die Weiterführung der Wurfparabel unter Nullhöhe [mit Nullhöhe meine ich hier die Abwurfhöhe, also hier 40m. Auftreffhöhe ist dann also nicht 0m, sondern -40m vom Turm aus betrachtet]: Dort fliegt er mit einer bestimmten Anfangsgeschwindigkeit weiter (die ganz allgemein wie groß ist?), und legt damit eine bestimmte Tiefe zurück und eine bestimmte waagerechte Strecke. Tiefe und waagerechte Strecke sind dann gegeben bzw. Wurfweite musst du noch zerlegen, wenn du den Wurf in die zwei Abschnitte zerlegst, wie ichs beschrieben habe.

Die Wurfparabel insgesamt kann auch als Funktionsgleichung dargestellt werden, diese Funktionsgleichung kann man sich aus den Gleichungen zur Charakterisierung des schrägen Wurfes herleiten.
(Und diese Gleichung hast du auch schon hingeschrieben, du musst dir nur noch mal überlegen, was die einzelnen Symbole deiner Gleichungen bedeuten und was deine Gleichungen aussagen...
bei dem hier

bbcinek89 · Anmeldungsdatum: 03.10.2010 Beiträge: 16

okay danke für die erklärung

ich habe mir das eben angeschaut

und für wurf-, -zeit, -höhe, -weite bei einem schrägen wurf hätte ich auch bei jeder formel 2 unbekannte

z.B. wurfweite
Sx = v0 * cos(a) * t
umgestellt auf v0 oder t
v0 = (cos(a) * t)/sx
v0 = (cos(30°) * t)/95m

für die höhe und zeit wär es das gleiche problem

fuss · Anmeldungsdatum: 25.05.2010 Beiträge: 519

du musst das Problem erweitern, die Zeit in der Formel für die Wurfweite ist die Gesamtflugzeit, also auch nach Durchlaufen der Abwurfhöhe.
Wenn du alles insgesamt (Wurfweite, Wurf"tiefe") betrachtest, kommst du aufs Ergebnis. Sprich: Noch eine Gleichung hinzunehmen, damit du 2 Unbekannte und 2 Gleichungen hast.
Oder du nimmst wie schon angesprochen die Formel für die Wurfparabel her.

bbcinek89 · Anmeldungsdatum: 03.10.2010 Beiträge: 16

I Sx = v0 * cos(a) * t
II Sy = v0 * t * sin(a) * (-g)/2 * t²

I Sx = v0 * cos(a) * t => t = v0 * cos(a)/Sx

t in II Sy = v0 * (v0 * cos(a)/Sx) * (-g)/2 * (v0 * cos(a)/Sx)²
0 = v0 * (v0 * cos(30°)/95m) * (-9,81m/s²)/2 (v0 *cos(30)/95m)²
Hier bin ich mir nicht sicher, ob ich es richtig gemacht habe
0 = v0² * cos(30°)/95m) * (-9,81m/s²) * v0² * cos(30)²/95m²
und hier weiß ich nicht weiter
aber im habe am ende ja v0
v0 einsetzen in t = v0 * cos(a)/Sx
dann habe ich t
und dann hätte ich keine unbekannten mehr

fuss · Anmeldungsdatum: 25.05.2010 Beiträge: 519

im Prinzip richtig, aber schau deine Gleichungen nochmal an.
Die Umstellung nach t, Gleichung für sy und der eingesetzte Wert für sy stimmen nicht.
Schreib das erst mal allgemein auf, und setze dann erst Werte ein.

Und jetzt das, was ich mit der Wurfparabel meinte: die Formel, die allgemein aus den Gleichungen hergeleitet wird, und die du hier schon reingeschrieben hast, nämlich
y(x) = x tan(b) - g/(2v0²*cos²(b)) * x²
Zur Übung kannst du ja mal schauen, wie man auf die Gleichung kommt.
Sie lefert für v0 das gleiche Ergebnis, wenn du für x und y die gegebenen Werte einsetzt.
Aber auch hier musst du aufpassen, dass du bei dem y nicht den gleichen falschen Wert, wie oben bei sy einsetzt.

bbcinek89 · Anmeldungsdatum: 03.10.2010 Beiträge: 16

okay habe mich eben nochmal rangesetzt und bin jetzt zu einem ergebnis gekommen

KUGEL 1:

s1x(t) = s01x + v01 * t * cos(b) = s01x + 95m (I)
s1y(t) = s01y + v01 * t * sin(b) - g/2 * t² = 0 (II)

s01y = h = 40m
s01x = der weg der den die kugel genommen hätte wäre sie von höhe 0 geworfen wurden

(I) nach t auflösung in in II einsetzen

(I) t=95m/v01 * cos(b)

(II) h + v01 * (95m/vo1 * cos(b)) * sin(b) - g/2 * ((95m)²/v01² * cos²(b)) = 0

=> h + 95m * tan(b) - g/2 * ((95m)²/v01² * cos²(b)) = 0

v01 = Wurzel(g * (95m)²/2 * (h + 95m * tan(b) * cos²(b)
vo1 = Wurzel(9,81m/s² * (95m)²/2 (40m + 95m * tan(30°) * cos²(30°)
vo1 = 24,9 m/s

(I) t = 95m/24,9m/s * cos30° = 4,4s

KUGEL 2:
t = 4,4s + dt = 4,4s + 1,2s = 5,6s
s2(t) = s02 + v02 * t - g/2 * t² = 0

s02 = h = 40m

v02 = (g/2 * t² - s02)/t = ((9,81m/s²)/2) - 40m)/5,6s = 20,3m/s

Ich hoffe ich habe es richtig gerechnet.

Danke für deine ausführlichen antworten.

fuss · Anmeldungsdatum: 25.05.2010 Beiträge: 519

so stimmts Thumbs up!

Askela · Gast

Ich hab eine ähnliche Aufgabe wie bbcinek damals, jedoch soll ich die Abwurfgeschwindigkeit des schiefen Wurfs und den Aufschlagswinkel berechnen.

Wenn ich nun

berechne nach dem gegebenen Schema, wie kann ich dann vorgehen um den Aufschlagwinkel, sowie die Geschwindigkeit (beim Aufprall) zu erhalten?

Meine Angaben sind

Abwurfhöhe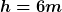

Reichweite

Abwurfwinkel

vielen Dank im Voraus

GvC · Anmeldungsdatum: 07.05.2009 Beiträge: 14861

Du solltest Deine Formel für die Anfangsgeschwindigkeit nochmal überprüfen. Da scheinst Du Kosinus und Tangens verwechselt zu haben.

Wenn Du die Anfangsgeschwindigkeit richtig raus hast, zerlegst Du sie in ihre horizontale und vertikale Komponenten. Die horizontale Komponente ist gleich der horizontalen Komponente der Endgeschwindigkeit. Die vertikale Komponente der Endgeschwindigkeit erhältst Du, indem Du die vertikale Komponente der Anfangsgeschwindigkeit in die Geschwindigkeitsgleichung für den senkrechten Wurf einsetzt. Der Aufschlagwinkel ist dann

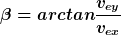Askela · Gast

hm ich hab die Herleitung von der Anfangsgeschwindigkeit mehrfach überprüft...

Danke für die Hilfe jetz hab ich beides

und der Winkel is dann

Als nächstes soll ich die allgemeine Reichweite bei einem Wurf am Hang berechnen (hangabwärts)... wäre super wenn mir da auch noch jemand helfen könnte
Hab ewig kein Physik mehr gehabt und versuch mich gerade mit Wiki und den Sachen hier durchzubeißen Hilfe

GvC · Anmeldungsdatum: 07.05.2009 Beiträge: 14861

Ist die Formel für die Anfangsgeschwindigkeit nicht eher

Askela · Gast

Ja danke stimmt...

naja die Werte ändern sich trotzdem nicht drastisch

bei der zweiten Aufgabe frag ich mich ob unter Reichweite die Strecke auf dem Hang betrachtet wird oder die echte Bewegung in x-Richtung

GvC · Anmeldungsdatum: 07.05.2009 Beiträge: 14861

Du könntest ja durchaus beides bestimmen. Beide Strecken hängen ja über den Kosinus des Neigungswinkel des Hanges zusammen.