| Autor |
Nachricht |
henry00
Anmeldungsdatum: 11.10.2010
Beiträge: 39
|
 henry00 Verfasst am: 14. Okt 2010 17:11 Titel: Kommutator Berechnen |
 |
|
Hallo zusammen
Habe probleme bei der folgenden Aufgabe:
 http://666kb.com/i/bniepf4iiabfwf9hw.jpg
Nun ja, in der vorlesung haben wir die operatoren wie folgt definiert. Ich verwende hierbei die Impulsbasis.
nun meine erste frage: Das "k", das bei der 2. gleichung rauskommt, ist eine reelle zahl oder?
Nun hab ich die e-fkt in einer reihe entwickelt.
ausserdem setze ich b=a/hquer
 - (i\frac{d}{dk} - k*b\frac{d}{dk}-i\frac{k^2b^2}{2}\frac{d}{dk} +\frac{k^3b^3}{6}\frac{d}{dk}+i\frac{k^4b^4}{24}\frac{d}{dk}...)] )
stimmt das soweit? Wenn ja, frage ich mich, was nun k genau ist in meiner reihenentwicklung. Wenn k einfach eine zahl ist, kann ich sie ja jeweils vor den ableitungsoperator ziehen und alles würde sich zu 0 aufheben. Wenn k allerdings eie variable ist nach der ich auch noch ableiten müsste, wird natürlich alles komplizierter mit der produktregel und so... Wer weiss mehr 
grüsse
henry |
|
 |
henry00
Anmeldungsdatum: 11.10.2010
Beiträge: 39
|
| henry00 Verfasst am: 14. Okt 2010 18:13 Titel: |
|
|
hallo, ich gleich nochmal. Hab da glaub was falsch gemacht.
in der aufgabe ist ja gegeben, dass
nun kommen in meiner reihenentwicklung folgende kommutatoren vor:
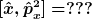
und höhere ordnungen von p_x. Gibt das auch alles i*hquer?
grüsse
henry |
|
|
Braino
Anmeldungsdatum: 23.11.2006
Beiträge: 57
Wohnort: Aachen
|
| Braino Verfasst am: 14. Okt 2010 18:17 Titel: |
|
|
Das k ist eine reelle Zahl, ja. Das liegt daran, dass der Impuls eine Observable und  ein selbstadjungierter Operator ist.
Deinen Ansatz kann ich auf die Schnelle nicht nachvollziehen. Du müsstest einfach nur die Exponentialfunktion in eine Reihe entwickeln und dann versuchen, deinen Ortsoperator einmal komplett durchzuschieben und dabei die Beziehung aus der Aufgabenstellung benutzen.
EDIT: Genau so. Deinen Kommutator  kriegst du ebenfalls aus dem gegebenen Kommutator raus. Denn: \hat p^{n-1}) . |
|
|
henry00
Anmeldungsdatum: 11.10.2010
Beiträge: 39
|
| henry00 Verfasst am: 14. Okt 2010 18:24 Titel: |
|
|
hi braino
Danke für die antwort.
Ja genau das wollte ich machen. Wenn ich aber die exp-fkt als reihe entwickle, bekomm ich ja terme wo der operator p_x auch in ordnung 2 und höher vorkommt. Wenn ich dann versuche, die operatoren zu gruppieren und sie als kommutator zusammenzufassen, bekomm ich eben zB
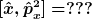
ich frag mich, ob das auch ihquer gibt (und all die höheren ordnungen auch... Verstehst du was ich meine? Ansonsten müsste ich das schnell mit latex machen...
lg
henry |
|
|
henry00
Anmeldungsdatum: 11.10.2010
Beiträge: 39
|
| henry00 Verfasst am: 14. Okt 2010 18:27 Titel: |
|
|
hi
wir schreiben grad etwas an uns vorbei, aber ich denke jetzt sollts klappen.^^
ok, du hast mir gegeben, dass
sollte da nicht noch ne eckige klammer auf der linken seite stehen? Denn sonst ists ja kein kommutator oder? |
|
|
Braino
Anmeldungsdatum: 23.11.2006
Beiträge: 57
Wohnort: Aachen
|
| Braino Verfasst am: 14. Okt 2010 18:48 Titel: |
|
|
Okay, das war jetzt missverständlich, ich meinte auch nicht den Kommutator direkt, denn den brauchst du auch so nicht, sondern der ist im Grunde ja gesucht. Bei der Rechnung kommst du auf:
] = \sum_{n=0}^{\infty} \frac 1 {n!}b^n \hat x \hat p^n - \exp(b \hat p) \hat x )
Und jetzt brauchst du ja , denn:
 \hat x = \sum_{n=0}^{\infty} \frac 1 {n!}b^n \left([\hat x, \hat p^n] + \hat p^n \hat x\right) - \exp(b\hat p) \hat x = \sum_{n=0}^{\infty} \frac 1 {n!}b^n [\hat x, \hat p^n] )
Es gilt also ] = \sum_{n=0}^{\infty} \frac 1 {n!}b^n [\hat x, \hat p^n]) .
Und jetzt kannst du diesen Kommutator durch den gegebenen ausrechnen:
\hat p^{n-1} - \hat p^n \hat x = (i\hbar+\hat p \hat x)\hat p^{n-1} - \hat p^n \hat x)
Das musst du solange fortsetzen, bis du das x einmal komplett durchgeschoben hast und der resultierende Term mit dem hinteren Term wegfällt. Der Rest ist dann dein Kommutator. |
|
|
henry00
Anmeldungsdatum: 11.10.2010
Beiträge: 39
|
| henry00 Verfasst am: 14. Okt 2010 19:07 Titel: |
|
|
hallo braino
besten dank für deine mühe und gute antwort. Ich hab das soweit alles nachvollziehen können. Nur bin ich etwas verwirrt, wo nun genau das ziel ist, denn meine reihe ist ja im prinzip unendlich lang. Wenn ich deinen letzten term mal ausmultipliziere bekomm ich:
\hat p^{n-1} - \hat p^n \hat x =i\hbar\hat p^{n-1}+\hat p \hat x\hat p^{n-1}- \hat p^n \hat x)
kann ich nun annehmen, dass gilt:
 ??
naja, oder anders gesagt: Ich versteh nicht ganz was du meinst mit x einmal komplett durchschieben, denn eben, meine exp-reihe ist ja unendlich lang...
lg und danke nochmal
henry |
|
|
Braino
Anmeldungsdatum: 23.11.2006
Beiträge: 57
Wohnort: Aachen
|
| Braino Verfasst am: 14. Okt 2010 19:22 Titel: |
|
|
Nein, nein, du kannst das nicht annehmen. Im Grunde geht es darum, den Kommutator kompakt als Summe darzustellen.
\hat p^{n-1} = i\hbar \hat p^{n-1} + \hat p (i\hbar + \hat p \hat x)\hat p ^ {n-2} = \sum \hdots + \hat p^n \hat x)
Du musst jetzt nur noch rausfinden, was die drei Pünktchen sind.  Das kann man dann noch weiter vereinfachen, aber wirst du sehen. |
|
|
henry00
Anmeldungsdatum: 11.10.2010
Beiträge: 39
|
| henry00 Verfasst am: 14. Okt 2010 20:19 Titel: |
|
|
hallo
ok, hab nun folgendes raus:
-\hat p_x^n \hat x)
richtig so? Mal abgesehen von der vereinfachung
glg
henry |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 14. Okt 2010 21:45 Titel: Re: Kommutator Berechnen |
|
|
| henry00 hat Folgendes geschrieben: | |
Auch wenn es dir nicht wirklich hilft; was du da schreibst ist formal falsch.
Die Differentialoperatoren gelten nur in der jeweiligen Darstellung und wirken auf die Wellenfunktion, nicht auf den Ket, denn ein Ket ist nicht x-abhängig.
Also z.B.
 = k \psi_k(x))
mit
 = <x|k> = e^{ikx})
und
 = y u_y(x))
mit
 = <x|y> = \delta(x-y))
Man erhält also die Wellenfunktion in x- bzw. k-Darstellung als Projektion mitels eines x- bzw. k-Eigenbras des Zustandes; allgemein
 = <x|\psi>)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 14. Okt 2010 22:51, insgesamt einmal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 14. Okt 2010 22:50 Titel: |
|
|
Noch zwei Tricks zur Berechnung von Kommutatoren.
1) Ganz allgemein gilt
Man sieht dies durch explizites hinschreiben
2) für die abstrakten Orts- und Impulsoperatoren darf man z.B. die x-Darstellung wählen und Kommutatoren wie folgt berechnen (hier im Beispiel mit x²)
 = -i x^2\partial_xf + i\partial_x(x^2f) = -i x^2\partial_xf + i(2xf+ x^2\partial_xf) = 2ixf \to [x^2, p] = 2ix)
Damit berechnet man leicht Kommutatoren der Form
, -i\partial_x]f(x))
und prinzipiell auch (wenngleich nicht so einfach)
, h(-i\partial_x)]f(x))
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Braino
Anmeldungsdatum: 23.11.2006
Beiträge: 57
Wohnort: Aachen
|
| Braino Verfasst am: 14. Okt 2010 23:30 Titel: |
|
|
| henry00 hat Folgendes geschrieben: | hallo
ok, hab nun folgendes raus:
richtig so? Mal abgesehen von der vereinfachung
glg
henry |
Hm, also was ist mit den Grenzen deiner Summe? Und für was hast du das raus? Wenn du die drei Pünktchen in meiner Gleichung oben berechnest, komst du auf einen Ausdruck, der einfach n mal  summiert. Wenn du das oben in den gesuchten Kommutator einsetzt, kannst du eine Indexverschiebung machen und dann wunderbar eine Exponentialfunktion erhalten. Ach ja, das, was TomS geschrieben hat, ist natürlich auch clever. |
|
|
|
Registrieren
Login
FAQ
Suchen
