| Autor |
Nachricht |
Xeal
Anmeldungsdatum: 29.05.2007
Beiträge: 243
|
 Xeal Verfasst am: 20. Jul 2010 20:33 Titel: Gaußsche Fehlerfortpflanzung Polynom 9. Grades Xeal Verfasst am: 20. Jul 2010 20:33 Titel: Gaußsche Fehlerfortpflanzung Polynom 9. Grades |
 |
|
Hallo Leute,
Ich stehe grade vor Folgendem Problem:
Ich habe eine Funktion mit einem Polynom 9. Grades angepasst:
=\sum_{j=0}^{9}a_j \cdot I^j)
I, sowie alle a_j sind mit einem Fehler behaftet.
Damit ergibt sich die Gaußsche Fehlerfortpflanzung zu:
=\sqrt{\left ( \left ( \sum_{j=1}^{9}j \cdot a_j \cdot I^{j-1} \right )\Delta I \right )^2 + \sum_{j=0}^{9}(I^j \cdot \Delta a_j)^2})
Ich hoffe, das stimmt...
Alles schön und gut, aber obige Fehlerformel beschreibt meinen Messfehler nicht gut, denn er wird durch den Faktor j in der ersten Summe dominiert und wird dadurch viel zu groß.
Wie löst man so etwas am besten?
Ich könnte, wenn ich es mir einfach machen will, den Fehler einfach auf xx % schätzen. Ob das aber legitim ist ?
Oder könnte man als abschätzung den Faktor j in der 1. Summe einfach weg lassen ?
Grüße
Holger
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 20. Jul 2010 21:28 Titel: Re: Gaußsche Fehlerfortpflanzung Polynom 9. Grades DrStupid Verfasst am: 20. Jul 2010 21:28 Titel: Re: Gaußsche Fehlerfortpflanzung Polynom 9. Grades |
 |
|
|
Wenn die Fehlerfortflanzung einen zu großen Fehler liefert, dann könnte das daran liegen, dass Du den Fehler von I überschätzt. Wie bist Du eigentlich bei der Regression vorgegangen?
|
|
 |
Xeal
Anmeldungsdatum: 29.05.2007
Beiträge: 243
|
 Xeal Verfasst am: 20. Jul 2010 22:47 Titel: Xeal Verfasst am: 20. Jul 2010 22:47 Titel: |
 |
|
Hi,
Ich glaube ehrlich gesagt nicht, dass der Fehler von I (hier der Strom) zu groß geschätzt wurde. Er wurde mit einem normalen Multimeter gemessen und wurde vom Hersteller zu 1% + 1 Digit angegeben. Bei anderen Fehlerfortpflanzungen liefert das auch sinnvolle ergebnisse.
Zu meiner Regression:
Es geht um das Anpassen der modifizierten Fermi-Funktion G in Abhängigkeit des Stroms. Die Messwerte dazu habe ich aus einer Staatsexamensarbeit bekommen.
Ich habe in Origin die Messwerte eingetragen und über einen nichtlinearen Fit angepasst (Polynomiell). Dabei hat origin anscheinend automatisch den Grad 9 gewählt. ich habe es auch mit Grad 7 oder 8 Versucht, das hat aber nicht gut gepasst.
Im Anhang mal mein Ergebnis.
| Beschreibung: |
|

Download |
| Dateiname: |
G-Funktion.pdf |
| Dateigröße: |
10.49 KB |
| Heruntergeladen: |
291 mal |
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 21. Jul 2010 02:04 Titel: dermarkus Verfasst am: 21. Jul 2010 02:04 Titel: |
 |
|
drei Gedanken dazu:
* Solche Terme der neunten Potenz scheinen mir zu ziemlich großen Abhängigkeiten der Werte voneinander führen zu können.
* Ein polynomieller Fit hoher Ordnung ist eher immer nur ein Mittel letzter Wahl, falls einem nichts besseres einfällt und man keine Ahnung hat, was für eine Funktion da physikalisch dahinterstecken soll.
Du sagst, das sei eine modifizierte Fermifunktion. Weißt du, wie eine Fermifunktion aussieht, und kannst du vielleicht sogar sagen, zu was für Änderungen oder Zusatzvariablen in diesen Termen es durch die Modifikation kommt, mit der du es zu tun hast? Mit so einer "intelligenter gewählten" Funktion treten künstliche Auswerteschwierigkeiten wie Polynome 9. Grades glaube ich nicht so schnell auf.
* Dass deine Fitfunktion die seltsamen Schlenker rechts oben im Diagramm mitmacht, scheint mir auf den ersten Blick etwas seltsam. Was für einen Kurvenverlauf würdest du physikalisch in diesem Bereich rechts oben erwarten? Könntest du dort sinnvollerweise auch eine deutlich glattere Funktion anfitten? (Könnte es dir dabei helfen, in betracht zu ziehen, dass die vertikalen und/oder horizontalen Fehlerbalken an den Messpunkten insbesonder in diesem Bereich auch etwas größer gewesen sein könnten, so dass eine glattere Kurve damit immer noch gut mit den mit solchen Fehlerbalken/Fehlerkreuzen versehenen Messpunkten übereinstimmt?)
|
|
 |
Xeal
Anmeldungsdatum: 29.05.2007
Beiträge: 243
|
 Xeal Verfasst am: 21. Jul 2010 09:22 Titel: Xeal Verfasst am: 21. Jul 2010 09:22 Titel: |
 |
|
Hallo Markus,
Vielen Dank für deine Antwort.
| Zitat: | | Ein polynomieller Fit hoher Ordnung ist eher immer nur ein Mittel letzter Wahl, falls einem nichts besseres einfällt und man keine Ahnung hat, was für eine Funktion da physikalisch dahinterstecken soll. |
Der Assistent hat empfohlen, die Funktion am Wendepunkt zu teilen, und im Bereich links und rechts ein Polynom anzusetzen. Dabei kann es passieren, dass die Funktion am wendepunkt nicht stetig bleibt. Daher wählt man für den Fit die grenzen der Datenpunkte etwas über den Wendepunkt hinaus.
Ich dachte mir eben, ob ich nun 2* ein Polynom 4. oder 5. Grades nehme, oder 1* ein Polynom 9. Grades macht nicht so den riesen Unterschied 
| Zitat: | | Du sagst, das sei eine modifizierte Fermifunktion. Weißt du, wie eine Fermifunktion aussieht, und kannst du vielleicht sogar sagen, zu was für Änderungen oder Zusatzvariablen in diesen Termen es durch die Modifikation kommt, mit der du es zu tun hast? Mit so einer "intelligenter gewählten" Funktion treten künstliche Auswerteschwierigkeiten wie Polynome 9. Grades glaube ich nicht so schnell auf. |
Ich werde mal schauen ob ich es rausfinde.
| Zitat: | | * Dass deine Fitfunktion die seltsamen Schlenker rechts oben im Diagramm mitmacht, scheint mir auf den ersten Blick etwas seltsam. Was für einen Kurvenverlauf würdest du physikalisch in diesem Bereich rechts oben erwarten? Könntest du dort sinnvollerweise auch eine deutlich glattere Funktion anfitten? (Könnte es dir dabei helfen, in betracht zu ziehen, dass die vertikalen und/oder horizontalen Fehlerbalken an den Messpunkten insbesonder in diesem Bereich auch etwas größer gewesen sein könnten, so dass eine glattere Kurve damit immer noch gut mit den mit solchen Fehlerbalken/Fehlerkreuzen versehenen Messpunkten übereinstimmt?) |
Du hast recht, der Schlenker ist mir auch aufgefallen.. Das Problem ist, dass mir für die angegebenen Datenpunkte keine Fehler bekannt sind (in der Staatsexamensarbeit werden keine angegeben).
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 21. Jul 2010 12:03 Titel: dermarkus Verfasst am: 21. Jul 2010 12:03 Titel: |
 |
|
Ah, dann wird es sicher am einfachsten sein, dem Tipp des Assistenten zu folgen. Denn dann bekommst du keine Polynome von Monster-hoher Ordnung, die, wie du gemerkt hast, Schwierigkeiten machen können.
Und obendrein fängt dein Fit dann nicht so schnell an, die kleinen Abweichungen rechts oben nachzumalen, die ich auf den ersten Blick weniger für physikalische Effekte, sondern eher für Messfehlerauswirkungen halten würde. Ein Fit kleinerer Ordnung geht da rechts oben dann sicher etwas "gerader" durch die Punkte durch und vermittelt einen etwas realistischeren Eindruck von den Fehlerbalken der Messpunkte in diesem Bereich da rechts oben.
Dieses zweigeteilte Polynom-anfitten ist dann sicher brauchbar genug, so dass du dich dann für den Zweck dieser Aufgabe nicht mit der genauen funktionalen Form einer Fermi-Kurve oder gar einer modifizierten Fermi-Kurve auseinanderzusetzen brauchst.
|
|
 |
Xeal
Anmeldungsdatum: 29.05.2007
Beiträge: 243
|
 Xeal Verfasst am: 21. Jul 2010 13:15 Titel: Xeal Verfasst am: 21. Jul 2010 13:15 Titel: |
 |
|
Hallo Markus,
Das beruhigt mich ein wenig. Allerdings habe ich mich doch ein wenig mit der Fermifunktion beschäftigt, und irgendwie kommt mir eine Sache ein wenig spanisch vor:
Diese modifizierte Fermi-Funktion G ist ja definiert als:
 \cdot F(Z,E))
Dabei ist F die Fermi-Funktion. Da ich in meinem Skript ein Diagramm zur Fermi Funktion habe, habe ich mir mal den spaß gemacht, und
 = (E/p) \cdot G) gegen die Energie aufgetragen. gegen die Energie aufgetragen.
Was dabei raus kam, ist im Anhang.
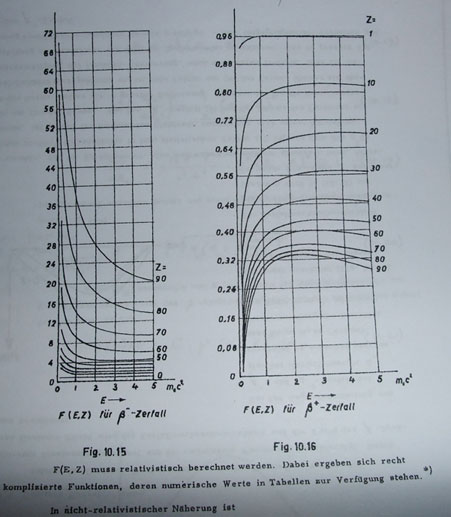
Weiterhin finden sich im Anhang zwei Graphen, die F(E,Z) als Funktion der Energie für den beta minus und beta plus zerfall darstellen.
In meinem Experiment (Beta-Spektroskopie) untersuche ich den Beta minus Zefall von  . .
Wie man sehen kann, stimmt der Verlauf von meinem F(E,Z) eher mit dem eines beta + zerfalls überein...
Zur Berechnung von F(E,Z) habe ich mal die im Skript gegebenen Werte mit in den Anhang gepackt (txt-datei). Die Werte habe ich genauer gesagt berechnet, sie stimmen aber mit denen im Skript überein.
| Beschreibung: |
|
| Dateigröße: |
46.08 KB |
| Angeschaut: |
7596 mal |
|
| Beschreibung: |
|

Download |
| Dateiname: |
fermifunktion.txt |
| Dateigröße: |
2.65 KB |
| Heruntergeladen: |
247 mal |
| Beschreibung: |
|

Download |
| Dateiname: |
Fermi-Funktion.pdf |
| Dateigröße: |
15.67 KB |
| Heruntergeladen: |
246 mal |
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 21. Jul 2010 13:29 Titel: dermarkus Verfasst am: 21. Jul 2010 13:29 Titel: |
 |
|
* Könnte es vielleicht einfach sein, dass in den Messdaten die Summe zweier Effekte drin ist, einer von einem beta-Minus-Zerfall und einer von einem beta-Plus-Zerfall? Falls es dich interessiert, so eine Funktion ausfindig zu machen, könnte es vielleicht Spaß machen, mal so eine Summenfunktion an die Daten anzufitten.
* allgemein gesagt: "modifizierte" Fermifunktion kann als Wort wohl noch alle möglichen Sachen bedeuten, denn außer der von dir genannten Möglichkeit gibt es wohl sicher auch je nach experimentellem Zusammenhang noch andere Möglichkeiten, eine Fermifunktion zu verändern (= zu modifizieren). Am Ende bedeutet das "modifiziert" in deinem Zusammenhang vielleicht einfach nur, dass der Zusatzeffekt, der in den dir vorliegenden experimentellen Daten vorkommt und eine Modifikation der Fermifunktion erforderlich macht, schlicht das Vorliegen zweier Zerfallsarten ist oder so.
|
|
 |
Xeal
Anmeldungsdatum: 29.05.2007
Beiträge: 243
|
 Xeal Verfasst am: 21. Jul 2010 14:23 Titel: Xeal Verfasst am: 21. Jul 2010 14:23 Titel: |
 |
|
Hallo,
Leider weiss ich nicht, wo die messdaten der G-Funktion in meinem Skript herkommen. Dort ist zwar eine Kopie der Staatsexamensarbeit vorhanden, allerdings ist dort nicht vermerkt wie die Werte zu stande kommen .....
 Allerdings steht in der Quelle, von der ich F als Funktion der Energie als Plot habe, dass die Fermifunktion relativistisch berechnet werden muss. Allerdings steht in der Quelle, von der ich F als Funktion der Energie als Plot habe, dass die Fermifunktion relativistisch berechnet werden muss.
Eine entsprechende Tabelle findet sich in Siegbahn: Beta- and Gamma-Spectroscopy, App. II (1955). Allerdings ist dort auch die modifizierte Fermi Funktion G aufgeschrieben. Ich habe nun auch diese Werte in ein Diagramm aufgetragen: der Verlauf stimmt überein.
Ich vermute, dass die Abweichungen von den Plots die ich in der Literatur gefunden habe daher kommen, dass der dargestellte Energiebereich bei mir deutlich größer ist.
Was ist denn eine Summenfunktion ?
|
|
 |
Xeal
Anmeldungsdatum: 29.05.2007
Beiträge: 243
|
 Xeal Verfasst am: 21. Jul 2010 14:49 Titel: Xeal Verfasst am: 21. Jul 2010 14:49 Titel: |
 |
|
So, ich habe das ganze jetzt mit einem Polynom 5. Grades im linken bereich gemacht.
Für große Ströme (und entsprechend größe Fehler der Ströme) wird der Fehler aber z.b. für einen Strom von 1396mA +- 15 mA immernoch wahnsinnig groß (in diesem fall ca. 6 mal so groß).
Liegt wohl auch daran, dass ich den Fehler des Stromes auf 1% geschätzt habe, d.h. bei großen messwerten wird der fehler größer. und nun ?
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 21. Jul 2010 19:54 Titel: dermarkus Verfasst am: 21. Jul 2010 19:54 Titel: |
 |
|
Mit dem kurzen Wort Summenfunktion meinte ich oben einfach nur eine Funktion, die eine Summe aus einer Funktion für einen beta-Plus -Zerfall und einer Funktion für einen Beta-Minus-Zerfall ist.
5. Ordnung ist immer noch recht hoch, da könnte es schon sein, dass der Fehler, den du so herausbekommst, ein bisschen größer ist.
Natürlich ist es oft schwierig, einen Fehlerbalken für eine Messung zu schätzen oder anzunehmen, die du nicht selbst gemacht hast, so dass du nicht sehen konntest, wie genau die Messgeräte waren, wie genau man die ablesen konnte, und welche Fehlerquellen in diesem Versuch jeweils konkret in Frage kamen. Die gemessene Kurve sieht insgesamt recht vernünftig aus. Vielleicht kommst du ja mithilfe eines plausiblen Fits und den dann noch auftretenden Abweichungen im Diagramm zu direkteren Abschätzungen für die tatsächlichen Messfehler in diesem Experiment?
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 21. Jul 2010 21:45 Titel: DrStupid Verfasst am: 21. Jul 2010 21:45 Titel: |
 |
|
| Xeal hat Folgendes geschrieben: | | Ich glaube ehrlich gesagt nicht, dass der Fehler von I (hier der Strom) zu groß geschätzt wurde. |
Da dir Fehlerfortpflanzung korrekt aussieht, wüsste ich aber nicht, was sonst noch als Fehlerursache in Frage kommt.
| Xeal hat Folgendes geschrieben: | | Ich habe in Origin die Messwerte eingetragen und über einen nichtlinearen Fit angepasst (Polynomiell). Dabei hat origin anscheinend automatisch den Grad 9 gewählt. ich habe es auch mit Grad 7 oder 8 Versucht, das hat aber nicht gut gepasst. |
Das hilft leider nicht wirklich weiter, solange wir nicht wissen, wie Origin den Fit durchführt. Ich vermute, dass dabei die Summe der Fehlerquadrate [f(x)-y]² minimiert wird. Das bedeutet aber, dass der Fehler von x auf Null gesetzt wurde. Wenn Du ihn in der Fehlerfortpflanzung mit einem Fehler größer Null rechnest, dann passt das nicht zusammen und könnte eine Ursache für Deine Probleme sein.
Dass der Grad des Polynoms vermutlich zu hoch ist, wurde Dir ja schon gesagt. Das könnte auch eine Ursache für den Fehler sein, wenn nämlich höhere Potenzen gar nichts zum Ergebnis beitragen (und deshalb sehr ungenau sind) und sich erst bei der Fehlerfortpflanzung bemerkbar machen.
|
|
 |
Xeal
Anmeldungsdatum: 29.05.2007
Beiträge: 243
|
 Xeal Verfasst am: 22. Jul 2010 16:09 Titel: Xeal Verfasst am: 22. Jul 2010 16:09 Titel: |
 |
|
Hallo Leute,
Danke nochmal für eure Hilfe.
Ich habe nochmal genau nachgedacht, und bin zu folgendem Schluss gekommen. Diese modifizierte Fermifunktion wurde relativistisch berechnet, also ist es schonmal falsch für den (errechneten) Strom einen Fehler abzuschätzen, der sich aus irgendwelchen Messgeräten ergibt.
Genauer gesagt, wird normalerweise die modifizierte Fermifunktion G in abhängigkeit vom Teilchenimpuls p errechnet.
Da mir die Methode jedoch nicht bekannt ist, habe ich p und G als fehlerfrei angenommen. Dann habe ich G gegen p aufgetragen, was qualitätiv aussieht wie G gg. I aufgetragen.
Ich habe die Funktion dann gesplittet und in Bereich A ein Polynom 5. Grades und in Bereich B ein Polynom 4. Grades angesetzt (vgl. Anhang).
Ich habe argumentiert, dass Unsicherheit von G aus der Fitprozedur resultiert.
| Beschreibung: |
|

Download |
| Dateiname: |
GFkt_Impuls.pdf |
| Dateigröße: |
8.03 KB |
| Heruntergeladen: |
261 mal |
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 22. Jul 2010 16:27 Titel: dermarkus Verfasst am: 22. Jul 2010 16:27 Titel: |
 |
|
Gratuliere, diese Fits sehen viel vernünftiger aus als das von oben mit dem Polynom 9.Grades 
|
|
 |
|
|


















 Allerdings steht in der Quelle, von der ich F als Funktion der Energie als Plot habe, dass die Fermifunktion relativistisch berechnet werden muss.
Allerdings steht in der Quelle, von der ich F als Funktion der Energie als Plot habe, dass die Fermifunktion relativistisch berechnet werden muss.
