| Autor |
Nachricht |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 21. Sep 2022 17:34 Titel: Erwartungswert |
 |
|
Hallo Leute!
Ich muss hier den Erwartungswert der z-Komponente des Drehimpulses berechnen. Das habe ich auch getan, aber mein Ergebnis stimmt mit der Lösung nicht überein. Habe ich mich verrechnet? Ich kann mir aber nicht erklären, warum meine Lösung falsch sein sollte. Könnt ihr BITTE einen Blick werfen?
| Beschreibung: |
|
Download |
| Dateiname: |
15B3252D-7C9D-480F-9C3F-E9629C4F99B3.jpeg |
| Dateigröße: |
71.43 KB |
| Heruntergeladen: |
93 mal |
|
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18065
|
| TomS Verfasst am: 21. Sep 2022 21:57 Titel: |
|
|
Ich denke, da gibt es ein Verständnisproblem mit der Notation.
Der Erwartungswert eines Operators im Zustand psi wird in der bra-let-Schreibweise als
notiert.
Dabei ist NICHT
 )
also nicht ket = Wellenfunktion!
Ich hoffe nicht, dass das irgendwo so behauptet wird.
Die Berechnung des Erwartungswertes für eine Wellenfunktion erfordert den Operator in Ortsdarstellung, in deinem Fall mittels der Ableitung.
Im 1-dim. Fall berechnet sich der Erwartungswert mittels des Integrals
wobei das psi im Integral die Wellenfunktion bezeichnet.
Im vorliegenden Fall ist es Quatsch, für ein 1-dim. endliches Intervall von einem Drehimpuls zu sprechen. Was soll sich in einer Dimension drehen können? Oder ist eigentlich eine Funktion im 3-dim. Raum gemeint? Wo sind dann die r- und theta-Abhängigkeit?
Zu deiner Berechnung:
Es ist unnötig, Sinus und Cosinus durch e-Funktionen auszudrücken - kann man aber natürlich machen. In deiner Berechnung fehlt die Integration.
In der roten Lösung ist es Quatsch, dass eine phi-Ableitung ganz rechts steht - worauf soll die wirken? In der letzten Zeile fehlt rechts das Integral. Ein Ausdruck
kann NIE gleich einer Funktion sein.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 21. Sep 2022 23:11, insgesamt 6-mal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18065
|
| TomS Verfasst am: 21. Sep 2022 22:13 Titel: |
|
|
Zur Berechnung - ich lasse mal diverse Konstanten weg.
 \, (- i \partial_\phi) \, \psi(\phi) \sim \int_0^{2\pi} d\phi \, \sin(\phi) \, (- i \partial_\phi) \, \sin(\phi) = -i \int_0^{2\pi} d\phi \, \sin(\phi) \, \cos(\phi) = 0)
Letzteres erkennt man sofort mittels der äquivalenten Integration
 \, \cos(\phi) )
und
 \, \cos(-\phi) = - \sin(\phi) \, \cos(\phi))
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
| frage1 Verfasst am: 22. Sep 2022 13:01 Titel: |
|
|
Erstmal danke für deine Erklärung!
Ich komme momentan nicht ganz mit. Ich hab das noch nicht wirklich verstanden. Ich hab deine Berechnung versucht nachzuvollziehen und hab's auch versucht nachzurechnen, aber so sieht mein aktueller Stand aus:
| Beschreibung: |
|
Download |
| Dateiname: |
EDAD31E4-E752-44BE-BD16-8B5785A88F5A.jpeg |
| Dateigröße: |
65.74 KB |
| Heruntergeladen: |
84 mal |
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18065
|
| TomS Verfasst am: 22. Sep 2022 13:15 Titel: |
|
|
Und was verstehst du jetzt nicht?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
| frage1 Verfasst am: 22. Sep 2022 13:45 Titel: |
|
|
|
Warum werden die Integrationsgrenzen auf einmal +π (pi) und -π ?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18065
|
| TomS Verfasst am: 22. Sep 2022 13:52 Titel: |
|
|
1) Wenn du auf ganz R definierte periodische Funktionen mit
 = f(\phi))
hast - so wie hier - dann sind diese Funktionen bzgl. jedes Startpunktes des Intervalls um 2*pi periodisch. Du kannst das Intervall also so verschieben,
ohne den Wert desselben zu verändern.
2) Wenn du das tust, siehst du sofort und ohne Rechnung, dass das Integral Null sein muss, da die linke Hälfte (von minus pi bis Null) exakt den negativen Beitrag der rechten Hälfte (von 0 bis pi) liefert; das ist die letzte Formel meines Beitrags. Wenn du diese Verschiebung nicht magst, musst du das Integral eben explizit ausrechnen.
Es geht also lediglich darum, zu sehen, dass Null herauskommt, ohne lang rumrechnen zu müssen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
| frage1 Verfasst am: 22. Sep 2022 14:45 Titel: |
|
|
Diese Vorgehensweise war mir nicht bekannt, da wir immer das Integral ausgerechnet hatten. Und in der Lösung steht einfach, dass das Integral (von 0 bis 2pi) 0 ergibt. Also sie haben die Verschiebung gar nicht berücksichtig. Wäre die Begründung in der Lösung falsch? Sie haben ja quasi nichts ausgerechnet.
Und zur Frage: Welche Messwerte können mit welcher Wahrscheinlichkeit auftreten? Wie muss ich hier vorgehen?
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18065
|
| TomS Verfasst am: 22. Sep 2022 15:46 Titel: |
|
|
| frage1 hat Folgendes geschrieben: | | Und in der Lösung steht einfach, dass das Integral (von 0 bis 2pi) 0 ergibt ... Wäre die Begründung in der Lösung falsch? Sie haben ja quasi nichts ausgerechnet. |
Na ja, es reicht, das zu wissen ;-)
Es gibt eine weitere Argumentation: das Funktionssystem
, \sin(nx)\}; n \in \mathbb{N}^+; \; x \in [0, 2\pi] )
stellt ein Orthonormalsystem dar (siehe Foriertransformation, kann man wissen). Damit folgt ebenfalls ohne Rechnung, dass das Integral Null ist.
| frage1 hat Folgendes geschrieben: | | Und zur Frage: Welche Messwerte können mit welcher Wahrscheinlichkeit auftreten? |
Was habt ihr denn über die die möglichen Messwerte für eine Observable gelernt?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
| frage1 Verfasst am: 24. Sep 2022 13:54 Titel: |
|
|
|
TomS, ich hab die Aufgabe immer noch nicht verstanden. Es steht ja, dass der Erwartungswert 0 ergibt, aber wie haben sie das ohne rechnen erkannt? Muss man nicht das Integral lösen? Also Substitutionsregel anwenden? Ich check´ die Aufgabe immer noch nicht...
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18065
|
| TomS Verfasst am: 24. Sep 2022 14:30 Titel: |
|
|
Du musst einfach verstehen, dass ein Integral
)
für eine beliebige Funktion f(x) exakt Null ist, wenn
 = -f(x))
gilt.
Und wenn du das nicht verstehst, dann berechnest du das am besten mal explizit, indem du das o.g. Integral aufteilst, einmal von -a bis 0, dann von 0 bis +a, und im ersten Integral y = -x substituierst.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
| frage1 Verfasst am: 25. Sep 2022 07:24 Titel: |
|
|
|
Die Substitution ist ja ziemlich zeitaufwendig. Ich versuche deine obige Erklärungen nachzuvollziehen, aber ich check immer die Aussage „eine beliebige Funktion … 0 ist, wenn …“ immer noch nicht. Ich kann mir darunter nichts vorstellen. Ich könnte auch das Integral lösen, aber wenn es doch leichtere Wege gibt die Aufgabe zu lösen, dann macht die Integration wenig Sinn.
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18065
|
| TomS Verfasst am: 25. Sep 2022 08:51 Titel: |
|
|
 = \int_{-a}^{0} dx \, f(x) + \int_{0}^{+a} dx \, f(x))
Substitution
 = a, \; y(x = 0) = 0)
im ersten Integral, zweites Integral stehen lassen
 \, f(-y) + \int_{0}^{+a} dx \, f(x))
Vertauschen der Integrationsgrenzen, also Integration von 0 bis +a, liefert nochmal ein Vorzeichen
 \, f(-y) + \int_{0}^{+a} dx \, f(x))
jetzt anwenden von
 = - f(y))
 \, (-) f(y) + \int_{0}^{+a} dx \, f(x) = -\int_{0}^{+a} dy \, f(y) + \int_{0}^{+a} dx \, f(x) = 0)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
| frage1 Verfasst am: 25. Sep 2022 13:24 Titel: |
|
|
TomS, ich hab versucht deine Rechenschritte anzuwenden, aber ich glaube ich hab da immer noch Schwierigkeiten, weshalb ich mit der Substitution gerechnet habe. Unten habe ich versucht mit der „Verschiebung“ zu rechnen, aber richtig schaut meine Rechnung nicht aus.
Und noch zu deiner Frage mit den Observablen: Observablen sind ja Messgrößen. Und jeder Observablen entspricht ein quantenmechanischer Operator. Wir haben Ort, Impuls, Energie Operatoren behandelt. Aber wie genau soll ich die 2. Frage lösen?
| Beschreibung: |
|
Download |
| Dateiname: |
E3CF1E2D-173A-4F0E-ACA7-FBB2C14D672E.jpeg |
| Dateigröße: |
375.42 KB |
| Heruntergeladen: |
59 mal |
|
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
| Nils Hoppenstedt Verfasst am: 25. Sep 2022 14:52 Titel: |
|
|
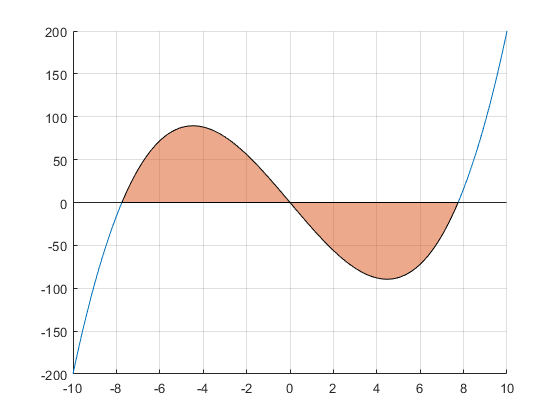
@frage1: Dass das Integral einer ungeraden Funktion über einen symmetrisch um 0 liegenden Integrationsbereich verschwindet, wird vielleicht durch folgendes Beispiel anschaulich klar. Die beiden Flächen links und rechts der Null sind aus Symmetriegründen gleich, haben aber entgegen gesetzte Vorzeichen. Ergo ist das Integral Null.
- Nils
| Beschreibung: |
|
| Dateigröße: |
12.56 KB |
| Angeschaut: |
648 mal |
|
_________________
Ihr da Ohm macht doch Watt ihr Volt! |
|
|
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
| frage1 Verfasst am: 25. Sep 2022 15:27 Titel: |
|
|
Ja, danke, so ist es anschaulich, aber was mir noch fehlt ist das rechnerische.
Warum die Grenzen -pi und + pi sind, verstehe ich. Aber wie soll ich das rechnerisch zeigen? Muss ich sin(phi) und cos(phi) aufteilen? Also von -pi bis 0 geht die Grenze der sinusfunktion und von 0 nach +pi geht die Grenze der cosinusfunktion?
|
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
| Nils Hoppenstedt Verfasst am: 25. Sep 2022 15:57 Titel: |
|
|
Den formalen Beweis hat TomS ja bereits gepostet. Für die Übungsaufgaben musst du das nicht jedesmal explizit nachrechnen. Das ist eine allseits bekannte Rechenregel (auch wenn du offenbar noch nie was davon gehört hast). Es genügt, dass du begründest, warum die Voraussetzungen hierfür erfüllt sind, also insbesondere wieso sin(x)*cos(x) ungerade ist. Und dann wendest du die Regel an und fertig.
_________________
Ihr da Ohm macht doch Watt ihr Volt! |
|
|
|
Registrieren
Login
FAQ
Suchen
