| Autor |
Nachricht |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 22. Sep 2022 14:49 Titel: Potentialtopf, kinetische Energie, Erwartungswert frage1 Verfasst am: 22. Sep 2022 14:49 Titel: Potentialtopf, kinetische Energie, Erwartungswert |
 |
|
Hallo!
Es geht hier wieder um den Erwartungswert des Impulses.
Ich kann die grün markierten Stellen nicht nachvollziehen. Wieso ist A1=A2 ?
Die e-Funktionen sind auf einmal verschwunden, wieso? Und wieso ist der Erwartungswert des Impulses 0 ? Und warum betrachtet man für den Erwartungswert des Impulses die Wände des Potentialtopfes?
Ich hab da noch einige Verständnisprobleme.
| Beschreibung: |
|

Download |
| Dateiname: |
C19EE760-FC0A-4140-B0C8-300019EA17EE.jpeg |
| Dateigröße: |
63.62 KB |
| Heruntergeladen: |
172 mal |
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 22. Sep 2022 21:26 Titel: Myon Verfasst am: 22. Sep 2022 21:26 Titel: |
 |
|
Wahrscheinlich sollte der Ansatz für den Bereich II lauten
=A_1e^{ikx}+A_2e^{-ikx})
Da phi(x)=0 gelten soll für den Bereich I (x<0) und da phi stetig sein soll, muss phi(0)=0 sein. Setzt man das in den Ansatz ein, folgt A1=-A2.
Zum Erwartungswert des Impulses: Wenn psi2 die Wellenfunktion zum 1. angeregten Zustand ist, so wäre der Erwartungswert für diesen Zustand
\frac{\partial}{\partial x}\psi_2(x)\,dx=0)
Es wird wieder über sin(k*x)*cos(k*x) integriert. Dies sollte für jeden Energie-Eigenzustand (Lösung der Schrödinger-Gleichung) gelten.
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 23. Sep 2022 12:34 Titel: frage1 Verfasst am: 23. Sep 2022 12:34 Titel: |
 |
|
Ich hab folgendes Ergebnis rausbekommen :
| Beschreibung: |
|

Download |
| Dateiname: |
AE5BACD9-E41B-4615-886A-270BF3824E1F.jpeg |
| Dateigröße: |
70.36 KB |
| Heruntergeladen: |
95 mal |
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 23. Sep 2022 12:54 Titel: Myon Verfasst am: 23. Sep 2022 12:54 Titel: |
 |
|
Da vom 1. angeregten Zustand geschrieben steht, hätte man wahrscheinlich auch einfach die Wellenfunktion, wie sie hier angegeben ist für n=2, verwenden können.
Den letzten Schritt in Deiner Rechnung konnte ich nicht recht nachvollziehen. Das Integral über sin(kx)*cos(kx) mit k=2*pi/a und diesen Grenzen sollte null ergeben.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 23. Sep 2022 12:59 Titel: Nils Hoppenstedt Verfasst am: 23. Sep 2022 12:59 Titel: |
 |
|
@frage1: du hast vergessen, die obere Grenze einzusetzen. Wegen sin(ka) = 0 kommt dann bei dir ebenfalls <p> = 0 heraus.
Nachdem man bereits gezeigt hat, dass A1 = -A2, kann man übrigens als Ansatz für die Wellenfunktion auch
psi(x) = A*sin(kx)
schreiben. Das vereinfacht die Rechnungen.
Viele Grüße,
Nils
_________________
Ihr da Ohm macht doch Watt ihr Volt! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 23. Sep 2022 13:00 Titel: TomS Verfasst am: 23. Sep 2022 13:00 Titel: |
 |
|
Warum löst du das selbe Integral nochmal und jetzt ganz anders?
Du hast sin(kx) und cos(kx), es muss also Null herauskommen, das weißt du schon aus der anderen Aufgabe.
Was ist der Fehler?
Du betrachtest sin(kx) im endlichen Intervall [0,a]. Es sind die für k erlaubten Werte zu bestimmen, die dafür sorgen, dass die genannten Randbedingungen bei x=0 und x=a erfüllt sind, d.h.
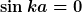
Du musst dir also überlegen, welche Werte für k in Frage kommen - und dann wirst du feststellen, dass du das Integral mittels Substitution wieder auf die Grenzen 0 bis 2*pi bringen kannst.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 23. Sep 2022 14:41 Titel: frage1 Verfasst am: 23. Sep 2022 14:41 Titel: |
 |
|
Myon, du hast recht. Ich glaube man muss sogar die Formel des 1-Dim. Kastenpotentials verwenden, aber wie genau soll ich da genau herangehen?
Leute, ich weiß ehrlich gesagt nicht, ob ich da richtig gerechnet habe (ich hoffe aber), aber so sieht mein aktueller Stand aus. Ich hab den Sinn der Aufgabe immer noch nicht verstanden.
Edit: Der Grund warum ich das Integral davor nicht lösen konnte, war, dass ich nicht wusste, dass k=npi/a ist.
| Beschreibung: |
|

Download |
| Dateiname: |
E51623D1-59F7-479F-9989-26580B62CE51.jpeg |
| Dateigröße: |
70.57 KB |
| Heruntergeladen: |
109 mal |
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 24. Sep 2022 19:52 Titel: Myon Verfasst am: 24. Sep 2022 19:52 Titel: |
 |
|
Bei der letzten Zeile bin ich nicht sicher, ob integriert wurde oder ob das Integralzeichen fehlt. Es ist jedenfalls noch nicht ganz richtig.
Bis auf Konstanten steht ja am Ende
\cos\left(\frac{n\pi}{a}x\right)\,dx=\frac{a}{n\pi}\int\limits_0^{n\pi}\sin u\,\cos u\,du)
Dieses Integral hat den Wert null für alle n, wie bei einer anderen Aufgabe erklärt wurde. Für den 1. angeregten Zustand wäre n=2.
Und sonst mit der Stammfunktion
-\cos^2(0))=0)
|
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 25. Sep 2022 07:27 Titel: frage1 Verfasst am: 25. Sep 2022 07:27 Titel: |
 |
|
Da ich die Verschiebung immer noch nicht verstanden habe, habe ich das Integral ausgerechnet. So sieht‘s dann aus:
Bei den Grenzen habe ich 2x ne 0. Kann das so stimmen?
| Beschreibung: |
|

Download |
| Dateiname: |
495570F4-B69C-4188-9762-F2C49A62A4A0.jpeg |
| Dateigröße: |
76.13 KB |
| Heruntergeladen: |
99 mal |
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 25. Sep 2022 09:08 Titel: Myon Verfasst am: 25. Sep 2022 09:08 Titel: |
 |
|
Jetzt sieht es gut aus. Einzig der Hinweis: wenn beim Integrieren substituiert wird, müssen im gleichen Schritt - nicht später - die Integralgrenzen ersetzt werden. Sonst gilt das Gleichheitszeichen nicht.
Eine Rücksubstitution ist hier nicht nötig, denn auch ohne eine solche wurde gezeigt, dass das Integral den Wert 0 hat.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Sep 2022 12:21 Titel: TomS Verfasst am: 25. Sep 2022 12:21 Titel: |
 |
|
| frage1 hat Folgendes geschrieben: | | Da ich die Verschiebung immer noch nicht verstanden habe … |

dann Substitution

anschließend Periodizität bzw. allgemein Eigenschaften der Winkelfunktionen ausnutzen, Rest siehe anderer Thread.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 25. Sep 2022 13:08 Titel: frage1 Verfasst am: 25. Sep 2022 13:08 Titel: |
 |
|
Alles klar, die Integralgrenzen habe ich nun ausgebessert.
Könne wir noch die zweite Frage durchgehen? Die lautet ja nämlich: Welche Messwerte für den Impuls des Elektrons sind in einer Einzelmessung möglich?
Muss ich dafür einfach die Formel p= +- hk verwenden?
| Beschreibung: |
|

Download |
| Dateiname: |
822F7284-83F9-4872-ABFC-9278D002D4D3.jpeg |
| Dateigröße: |
73.82 KB |
| Heruntergeladen: |
81 mal |
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Sep 2022 13:23 Titel: TomS Verfasst am: 25. Sep 2022 13:23 Titel: |
 |
|
Was genau habt ihr denn dazu gelernt?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 25. Sep 2022 13:38 Titel: frage1 Verfasst am: 25. Sep 2022 13:38 Titel: |
 |
|
TomS, ich habe die Frage schon in einem anderen Thread beantwortet.
Mehr zu den Observablen weiß ich leider auch nicht. Wir haben auch überprüft, ob eine Funktion Eigenfunktion zu einem Operator ist.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 25. Sep 2022 16:05 Titel: Myon Verfasst am: 25. Sep 2022 16:05 Titel: |
 |
|
Ich bin da leider selber unsicher. Die möglichen Messergebnisse für den Impuls sind die Eigenwerte des Impulsoperators. Für Funktionen der Form
=e^{ikx}, \quad k\neq0, \text{ reell};\quad 0\leq x\leq a)
gilt
)
Dass k die Werte

annimmt, kann man sich vielleicht noch damit erklären, dass dann eine Linearkombination der

jeweils eine Eigenfunktion des Hamilton-Operators ergibt. Allerdings erfüllen diese Funktionen die Stetigkeitsbedingungen nicht, welche bei der Lösung der Schrödingergleichung verlangt wurden.
Das Umgekehrte, dass man aus Linearkombinationen der 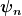 (Eigenfunktionen des Hamilton-Operators) Eigenfunktionen des Impulsoperators zusammenbaut, scheint leider nicht so einfach zu gehen. (Eigenfunktionen des Hamilton-Operators) Eigenfunktionen des Impulsoperators zusammenbaut, scheint leider nicht so einfach zu gehen.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Sep 2022 16:09 Titel: TomS Verfasst am: 25. Sep 2022 16:09 Titel: |
 |
|
1) Die prinzipiell möglichen Messwerte einer Observablen entsprechen den Eigenwerten des zugehörigen Operators A.
2) Die Wahrscheinlichkeit des Auftretens eines Messwertes a im Zustand psi folgt aus

Ein Messwert kann nur dann auftreten, wenn die Wahrscheinlichkeit ungleich Null ist, also nur dann, wenn

In deinem Fall sind dies gerade die nicht-verschwindenden Koeffizienten in der Entwicklung.
Für welchen Zustand stellst du die Frage?
Achtung: es sind nur Funktionen erlaubt, die die Randbedingungen im Potentialtopf bei x=0 und x=a respektieren. Das sind nicht die e-Funktionen!
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 25. Sep 2022 16:50 Titel: frage1 Verfasst am: 25. Sep 2022 16:50 Titel: |
 |
|
|
Sind das dann nicht die Werte - ih A? Ich bin verwirrt.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 25. Sep 2022 17:59 Titel: TomS Verfasst am: 25. Sep 2022 17:59 Titel: |
 |
|
Nochmal dazu:
| frage1 hat Folgendes geschrieben: | | Sind das dann nicht die Werte - ih A? Ich bin verwirrt. |
| TomS hat Folgendes geschrieben: | 1) Die prinzipiell möglichen Messwerte einer Observablen entsprechen den Eigenwerten des zugehörigen Operators.
2) In deinem Fall sind dies gerade die nicht-verschwindenden Koeffizienten in der Entwicklung. |
Für welchen Zustand stellst du die Frage? Verstehst du, warum der konkrete Zustand wichtig ist?
Wie genau lautet der hier relevante Operator?
Wie lauten die prinzipiell möglichen Eigenwerte dieses Operators? Und welche davon kommen für den konkreten Zustand im Frage?
| TomS hat Folgendes geschrieben: | | Achtung: es sind nur Funktionen erlaubt, die die Randbedingungen im Potentialtopf bei x=0 und x=a respektieren. Das sind nicht die e-Funktionen! |
Die Randbedingung bei Null lautet
 = 0)
d.h.

erfüllen diese nicht.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 26. Sep 2022 10:55 Titel: frage1 Verfasst am: 26. Sep 2022 10:55 Titel: |
 |
|
Nein, ich verstehe leider nicht warum dieser Zustand wichtig ist. Ich hab da noch Verständnisprobleme.
Der Impulsoperator lautet ja -ih d/dx. Ich muss ja diesen Operator auf die Funktion wirken lassen und überprüfen, ob die Funktion eine Eigenfunktion ist. Somit kommt man dann auch auf die Eigenwerte.
Außerdem kann ich auch nicht nachvollziehen warum die Amplituden innerhalb der Wände 0 sind. Und warum betrachtet man hier für den Erwartungswert des Impulses die Wände des Topfes? Ich hab da noch Verständnisprobleme. Könntest du mir das noch einmal in einfachen Worten erklären?
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 26. Sep 2022 12:27 Titel: TomS Verfasst am: 26. Sep 2022 12:27 Titel: |
 |
|
| frage1 hat Folgendes geschrieben: | | Ich muss ja diesen Operator auf die Funktion wirken lassen und überprüfen, ob die Funktion eine Eigenfunktion ist. Somit kommt man dann auch auf die Eigenwerte. |
Nein. Das ist nicht das, was ich geschrieben habe.
Was machst du, wenn es keine Eigenfunktion ist? Welche Messwerte kommen dann in Frage?
Nochmal:
1) Die prinzipiell möglichen Messwerte einer Observablen entsprechen den Eigenwerten des zugehörigen Operators.
Der von dir genannte Operatator ist richtig. Prinzipiell sind alle seine Eigenwerte als Messwerte möglich. D.h. es sind alle Eigenfunktionen mit allen Eigenwerten zu bestimmen. Das führt auf die bekannten Sinusfunktionen, die in den Wänden des Topfes verschwinden und daher einen Knoten an den Wänden bei x=0 und x=a aufweisen. Weil Knoten vorliegen, sind also nur diskrete Werte für k zulässig, nummeriert durch die natürlichen Zahlen n. Das Ergebnis hast du schon. Die e-Funktionen sowie die Cosinus-Funktionen sind offensichtlich nicht zulässig.
2) Wie ich oben geschrieben habe, können nur zu den Eigenfunktion, die in einem gegebenen Zustand enthalten sind, auch die entsprechenden Eigenwerte als Messwerte auftreten. Deswegen die Frage, für welchen Zustand du die möglichen Eigen- und damit Messwerte bestimmen sollst.
Die Eigenfunktionen müssen in den Wänden eines unendlichen Potentialtopfes verschwinden, da der Erwartungswert für die potentielle Energie V mit

offensichtlich sinnlos wird, wenn psi nicht exakt Null ist
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 26. Sep 2022 14:56 Titel: TomS Verfasst am: 26. Sep 2022 14:56 Titel: |
 |
|
Nochmal was grundsätzliches.
Du wirst das alles nicht dadurch verstehen, indem du Aufgaben rechnest.
Aufgaben zu rechnen hilft, den Stoff aus der Vorlesung anhand praktischer Beispiele besser zu verstehen und die Rechentechnik zu festigen.
Aufgaben zu rechnen hilft nicht dabei, ein konzeptionelles Verständnis zu erwerben - allenfalls, dieses zu festigen. Dazu musst du in der Lage sein, z.B. Fragen zu beantworten wie
Was ist die Bedeutung der Wellenfunktion?
Welcher Lösungen der Schrödingergleichung sind in einem bestimmten Fall physikalisch sinnvoll? Oder sinnlos?
Welche Bedeutung haben die Eigenwerte und Eigenfunktionen eines bestimmten Operators?
Wie ist ein Zustand mathematisch definiert? Was bedeutet das?
Welche Messwerte können in einem bestimmten Zustand auftreten? Mit welcher Wahrscheinlichkeit?
Was bedeutet der Übergang zwischen zwei Zuständen? Welche Regeln gelten dabei? Warum, bzw. welche physikalische Überlegung steckt dahinter?
Was ist in einem konkreten Fall überhaupt zu berechnen? Warum genau dieses? Warum nicht etwas anderes?
Dazu benötigst du eine gute Vorlesung, ein gutes Skript oder ein Buch. Außerdem hilfreich ist eine Lern- bzw. Diskussionsgruppe.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 26. Sep 2022 21:05 Titel: frage1 Verfasst am: 26. Sep 2022 21:05 Titel: |
 |
|
TomS, ich möchte mich wirklich sehr bei dir bedanken für all deine Erlärungen!
Ich werde mir das alles noch verinnerlichen, aber momentan bleibt mir nichts anderes übrig als die Rechnungen zu verstehen.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 26. Sep 2022 22:43 Titel: TomS Verfasst am: 26. Sep 2022 22:43 Titel: |
 |
|
M.M.n. zwar die falsche Reihenfolge … aber es ist deine Entscheidung.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
frage1
Anmeldungsdatum: 20.02.2021
Beiträge: 569
Wohnort: bayern
|
 frage1 Verfasst am: 26. Sep 2022 23:14 Titel: frage1 Verfasst am: 26. Sep 2022 23:14 Titel: |
 |
|
|
Natürlich ist das eine falsche Entscheidung, aber uns wurde ja nichts anderes beigebracht außer die Rechnungen zu verstehen... ich werde mir sowieso ein lehrbuch holen und mir den stoff beibringen, aber ich muss diese Aufgaben können und (momentan) die Rechnungen verstehen, da es sich zeitlich anders nicht mehr ausgeht...
|
|
 |
|















