| Autor |
Nachricht |
commanderkirsch
Anmeldungsdatum: 20.01.2022
Beiträge: 6
Wohnort: Bremen
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 21. Jan 2022 12:26 Titel: Mathefix Verfasst am: 21. Jan 2022 12:26 Titel: |
 |
|
zu b)
Die Kugel hat nur eine horizontale Geschwindigkeitskomponente an dem Punkt, an dem die Höhe der Flugbahn das Maximum erreicht hat:
 - g\cdot t = 0 \rightarrow t_{max} = \frac{v_0\cdot \sin(\alpha )}{g} )
Maximale Höhe
\cdot t_{max}- \frac{1}{2} \cdot g\cdot t_{max}^{2} = v_0\cdot \sin(\alpha )\cdot \frac{v_0\cdot \sin(\alpha )}{g} - \frac{1}{2} \cdot g\cdot (\frac{v_0\cdot \sin(\alpha )}{g})^{2})
 }{2\cdot g}
<br />
)
Bestimmung l_1
 = \frac{y_{max}}{l_1} = \frac{v_0^{2} \cdot \sin^{2} (\alpha ) }{l_1\cdot 2\cdot g} )
 }{ 2\cdot g \cdot \tan(\beta )})
) aus a) aus a)
Zeige bitte Deine Berechnung.
Zuletzt bearbeitet von Mathefix am 21. Jan 2022 13:51, insgesamt einmal bearbeitet |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
 DrStupid Verfasst am: 21. Jan 2022 13:13 Titel: DrStupid Verfasst am: 21. Jan 2022 13:13 Titel: |
 |
|
Ich würde es über die Energieerhaltung lösen. Beim Verlassen der Kurve hat die Kugel die volle Geschwindigkeit 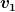 . Am Gipfelpunkt hat sie nur noch die horizontale Geschwindigkeitskomponente . Am Gipfelpunkt hat sie nur noch die horizontale Geschwindigkeitskomponente  und ist dafür um und ist dafür um  höher geflogen. Damit gilt für die Summe aus kinetischer und potentieller Energie (mit Nullpunkt am Ende der Kurve) höher geflogen. Damit gilt für die Summe aus kinetischer und potentieller Energie (mit Nullpunkt am Ende der Kurve)

Auflösung nach  liefert das Ergebnis von Mathefix. liefert das Ergebnis von Mathefix.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 21. Jan 2022 14:17 Titel: Mathefix Verfasst am: 21. Jan 2022 14:17 Titel: |
 |
|
zu c)
Die kinetische Energie der Kugel am Auftreffpunkt wird umgewandelt in
- Reibarbeit E_r
- Hubarbeit E_h
Wenn ich Zeit habe, helfe ich weiter.
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
 DrStupid Verfasst am: 21. Jan 2022 16:08 Titel: DrStupid Verfasst am: 21. Jan 2022 16:08 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | zu c)
Die kinetische Energie der Kugel am Auftreffpunkt wird umgewandelt in
- Translationsenergie E_t
- Rotationsenergie E_r
- Reibarbeit E_mü
- Hubarbeit E_h
|
Da die Kugel nach dem Auftreffen anscheinend nicht abprallen soll, handelt es sich um einen unelastischen Stoß, bei dem zusätzlich Energie verloren geht. Der normale Anteil der Aufprallgeschwindigkeit verschwindet einfach und es bleibt nur die Geschwindigkeitskomponente parallel zur Rampe übrig.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 21. Jan 2022 16:14 Titel: Mathefix Verfasst am: 21. Jan 2022 16:14 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | zu c)
Die kinetische Energie der Kugel am Auftreffpunkt wird umgewandelt in
- Translationsenergie E_t
- Rotationsenergie E_r
- Reibarbeit E_mü
- Hubarbeit E_h
|
Da die Kugel nach dem Auftreffen anscheinend nicht abprallen soll, handelt es sich um einen unelastischen Stoß, bei dem zusätzlich Energie verloren geht. Der normale Anteil der Aufprallgeschwindigkeit verschwindet einfach und es bleibt nur die Geschwindigkeitskomponente parallel zur Rampe übrig. |
@DrStupid
Die Überlegung hatte ich auch. Mir ist nicht klar, ob die Kugel beim Verlassen der Kurve rotiert oder ob sie in der "Anlaufstrecke" nur gleiten soll. Wenn sie nicht rotiert muss sie auf der Strecke Delta l beschleunigt werden. Muss nochmal nachdenken.
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
 DrStupid Verfasst am: 21. Jan 2022 16:29 Titel: DrStupid Verfasst am: 21. Jan 2022 16:29 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | | Mir ist nicht klar, ob die Kugel beim Verlassen der Kurve rotiert oder ob sie in der "Anlaufstrecke" nur gleiten soll. |
Da die Beschleunigung und Umlenkung reibungsfrei sein soll, könnte sie danach nur dann rotieren, wenn sie schon vor dem Abschuss rotiert hat. Dann wäre die Aufgabe aber nicht lösbar. Also müssen wir davon ausgehen, dass sie nicht rotierend auf die Rampe prallt und erst danach anfängt zu rollen. Ich meine mich zu erinnern, dass es dafür eine eindeutige Lösung gibt - selbst wenn man den Reibungskoeffizient nicht kennt. Wenn nicht vorgegeben wäre, dass das entlang einer von Null verschiedenen Strecke passiert, könnte man das gleich zusammen mit dem unelastischen Stoß abhandeln.
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
 DrStupid Verfasst am: 21. Jan 2022 17:08 Titel: DrStupid Verfasst am: 21. Jan 2022 17:08 Titel: |
 |
|
Ich hab's jetzt mal für den Fall durchgerechnet, dass die Kugel unmittelbar nach dem Aufprall die Geschwindigkeit  parallel zur Rampe hat und noch nicht rotiert. Dann gehe ich davon aus, dass am Auflagepunkt der Impuls parallel zur Rampe hat und noch nicht rotiert. Dann gehe ich davon aus, dass am Auflagepunkt der Impuls 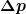 auf die Kugel übetragen wird. Damit wird sie nicht nur gebremst, sondern erhält auch den Drehimpuls auf die Kugel übetragen wird. Damit wird sie nicht nur gebremst, sondern erhält auch den Drehimpuls

mit

Wenn sie anschließend ohne Schlupf rollen soll, dann muss für die Geschwindigkeit

gelten. Alles zusammen ergibt

Von da an geht es dann mit der Energieerhaltung weiter.
Wenn man c) wörtlich nimmt, dann muss man 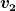 allerdings gar nicht berechnen, denn allerdings gar nicht berechnen, denn  soll ja nicht absolut, sondern in Abhängigkeit von soll ja nicht absolut, sondern in Abhängigkeit von 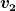 angegeben werden. angegeben werden.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 22. Jan 2022 12:20 Titel: Mathefix Verfasst am: 22. Jan 2022 12:20 Titel: |
 |
|
Durch die Reibung erfährt die Kugel ein Drehmoment
x -Achse = parallel zur Rampe
(1) Summe der Kräfte in x-Richtung = 0
 - F_R - m\cdot a = 0 )
(2) Summe der Momente = 0


Einsetzen in (1)
 }{1+\frac{I}{m\cdot r^{2} } } )
 )
v_2 = 0 am Ende der Rampe
 -a \cdot t = 0 \rightarrow t = \frac{v_1 \cdot \cos(\beta ) }{a})
 )^{2} }{2\cdot a} )
 )
- \Delta l )
|
|
 |
commanderkirsch
Anmeldungsdatum: 20.01.2022
Beiträge: 6
Wohnort: Bremen
|
 commanderkirsch Verfasst am: 23. Jan 2022 13:21 Titel: commanderkirsch Verfasst am: 23. Jan 2022 13:21 Titel: |
 |
|
[quote="Mathefix"]zu b)
Die Kugel hat nur eine horizontale Geschwindigkeitskomponente an dem Punkt, an dem die Höhe der Flugbahn das Maximum erreicht hat:
[latex]v_y = v_0\cdot \sin(\alpha ) - g\cdot t = 0 \rightarrow t_{max} = \frac{v_0\cdot \sin(\alpha )}{g} [/latex]
Maximale Höhe
[latex]y_{max} = v_0\cdot \sin(\alpha )\cdot t_{max}- \frac{1}{2} \cdot g\cdot t_{max}^{2} = v_0\cdot \sin(\alpha )\cdot \frac{v_0\cdot \sin(\alpha )}{g} - \frac{1}{2} \cdot g\cdot (\frac{v_0\cdot \sin(\alpha )}{g})^{2}[/latex]
[latex]y_{max} = \frac{v_0^{2} \cdot \sin^{2} (\alpha ) }{2\cdot g}
[/latex]
Bestimmung l_1
[latex]\tan(\beta ) = \frac{y_{max}}{l_1} = \frac{v_0^{2} \cdot \sin^{2} (\alpha ) }{l_1\cdot 2\cdot g} [/latex]
[latex]l_1 = \frac{y_{max}}{l_1} = \frac{v_0^{2} \cdot \sin^{2} (\alpha ) }{ 2\cdot g \cdot \tan(\beta )}[/latex]
[latex]v_0^{2}(h_1)[/latex] aus a)
Zeige bitte Deine Berechnung.[/quote]
Energieerhaltung
[latex]\frac{1}{2}cx^2=mgh+\frac{1}{2}mv^2[/latex]
durch umformen nach v kam raus
[latex]v=\sqrt{4gh}[/latex]
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 23. Jan 2022 13:34 Titel: Mathefix Verfasst am: 23. Jan 2022 13:34 Titel: |
 |
|
| commanderkirsch hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | zu b)
) aus a) aus a)
Zeige bitte Deine Berechnung. |
Energieerhaltung

durch umformen nach v kam raus
 |
Wie das denn?
^{2} = \frac{1}{2} \cdot m\cdot v_1^{2}+ m\cdot g\cdot h_1)
^{2} - 2\cdot g\cdot h_1 })
|
|
 |
commanderkirsch
Anmeldungsdatum: 20.01.2022
Beiträge: 6
Wohnort: Bremen
|
 commanderkirsch Verfasst am: 23. Jan 2022 14:32 Titel: commanderkirsch Verfasst am: 23. Jan 2022 14:32 Titel: |
 |
|
|
hab alles was gegeben war eingesetzt
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
 Mathefix Verfasst am: 23. Jan 2022 19:31 Titel: Mathefix Verfasst am: 23. Jan 2022 19:31 Titel: |
 |
|
| commanderkirsch hat Folgendes geschrieben: | | hab alles was gegeben war eingesetzt |
ok
|
|
 |
|
















