| Autor |
Nachricht |
Marietra
Anmeldungsdatum: 12.06.2021
Beiträge: 4
|
 Marietra Verfasst am: 12. Jun 2021 13:29 Titel: Schleuderbrett Formeln Marietra Verfasst am: 12. Jun 2021 13:29 Titel: Schleuderbrett Formeln |
 |
|
Meine Frage:
Hallo,
für ein Uni Projekt (kein Physik Studiengang) muss ich eine Kugelbahn Simulation programmieren und diese muss ein bewegliches Element enthalten. Hierbei habe ich mich für ein Schleuderbrett, also eine Art Wippe entschieden. Auf der einen Seite der Wippe liegt eine Kugel, auf die andere Seite fällt eine andere Kugel aus der Höhe herunter, sodass die erste nach oben geschleudert wird.
Kann mir jemand dabei helfen, wie ich die Beschleunigung bzw. Geschwindigkeit der nach oben geschleuderten Kugel berechnen kann, wenn Masse beider Kugeln und Fallhöhe bekannt sind? Die Flugbahn der zweiten Kugel kann dabei erstmal vernachlässigt werden, also sie soll erstmal nur senkrecht zu der Wippe fliegen.
Meine Ideen:
Mein Ansatz wäre, da ja die potenzielle in die kinetische umgewandelt wird und diese dann auf die zweite Kugel übertragen wird, aus dieser kinetischen Energie mit der Masse der zweiten Kugel deren Geschwindigkeit auszurechnen. Nur bin ich etwas ratlos wie ich das anstellen soll, da ich überhaupt keine Ahnung von Physik habe. |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 12. Jun 2021 15:20 Titel: Mathefix Verfasst am: 12. Jun 2021 15:20 Titel: |
 |
|
Deine Idee mit dem Energie Erhaltungssatz ist richtig.
Die Masse der Wippe bleibt unberücksichtigt.
Die Wippe mit der Länge l sei im Abstand a vom linken Ende gelagert und habe ein Auflager mit der Höhe b.
Am linken Ende ist eine Kugel mit der Masse m_l aufgelegt. Die Wippe ist also nach links geneigt und berührt den Boden.
Die rechte Kante hat über dem Boden die Höhe

In der Höhe h_0 befindet sich die Masse m_r über dem rechten Ende und
durchfällt die Höhe

Dadurch wird die potentielle Energie
 )
freigesetzt.
Die Wippe kippt nach rechts und berührt den Boden.
Höhe der linken Seite

Um diese Höhe wird die Masse m_l angehoben und auf die Geschwindigkeit v_l beschleunigt.
Es gilt

 = m_l \cdot g\cdot h_l + \frac{1}{2} \cdot m_l\cdot v_l^{2} )
v_l ist die Geschwindigkeit mit der die Masse m_l die Wippe verlässt:
-\frac{b}{l-a}) }
<br />
)
Auf diese Geschwindigkeit wird m_l über die Höhe h_l beschleunigt


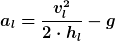
Zuletzt bearbeitet von Mathefix am 13. Jun 2021 12:35, insgesamt 3-mal bearbeitet |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 12. Jun 2021 15:33 Titel: Myon Verfasst am: 12. Jun 2021 15:33 Titel: |
 |
|
|
@Mathefix: nur, was mir grad durch den Kopf gegangen ist: ein Problem wäre, wenn die herunterfallende Kugel eine grössere Masse hätte, als diejenige, die durch die Wippe hochgeschleudert wird. Denn in diesem Fall würde nicht die ganze kinetische Energie übergeben, sondern die schwerere Kugel würde mit der Wippe mit einer gewissen Geschwindigkeit auf den Boden stossen. |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 12. Jun 2021 18:00 Titel: Mathefix Verfasst am: 12. Jun 2021 18:00 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | @Mathefix: nur, was mir grad durch den Kopf gegangen ist: ein Problem wäre, wenn die herunterfallende Kugel eine grössere Masse hätte, als diejenige, die durch die Wippe hochgeschleudert wird. Denn in diesem Fall würde nicht die ganze kinetische Energie übergeben, sondern die schwerere Kugel würde mit der Wippe mit einer gewissen Geschwindigkeit auf den Boden stossen. |
Ich denke, dass die potentielle Energie der herunterfallenden Kugel, die Masse der ruhenden Kugel und die Position und Höhe des Auflagers bestimmen, ob das rechte Ende der Wippe
a) den Boden gerade tangiert
b) auf den Boden stösst
c) den Boden nicht erreicht
Ich habe den einfachen fall a) behandelt. b) und c) hatte ich im Kopf, aber keinen zielführenden Lösungsansatz.
Werde das neu denken vlllt. mit Impulserhaltung, Massenträgheit ... |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 13. Jun 2021 14:05 Titel: Mathefix Verfasst am: 13. Jun 2021 14:05 Titel: |
 |
|
Ich habe meine Rechnung etwas vereinfacht. Die Verformungsarbeit durch den Stoss der Wippe bleibt unberücksichtigt, da ich den Stossfaktor nicht ermitteln kann. Ebenfalls wird die Verformungsarbeit durch Biegen des Bretts nicht berüksichtigt, genau so wie der Luftwiderstand ...
Es ist eine einfache Modellrechnung. Ich kann diese, wenn gewünscht, noch um die Hubarbeit des Brettschwerpunkts und die Rotationsenergie des Bretts ergänzen. |
|
 |
Marietra
Anmeldungsdatum: 12.06.2021
Beiträge: 4
|
 Marietra Verfasst am: 14. Jun 2021 17:10 Titel: Marietra Verfasst am: 14. Jun 2021 17:10 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | Ich habe meine Rechnung etwas vereinfacht. Die Verformungsarbeit durch den Stoss der Wippe bleibt unberücksichtigt, da ich den Stossfaktor nicht ermitteln kann. Ebenfalls wird die Verformungsarbeit durch Biegen des Bretts nicht berüksichtigt, genau so wie der Luftwiderstand ...
Es ist eine einfache Modellrechnung. Ich kann diese, wenn gewünscht, noch um die Hubarbeit des Brettschwerpunkts und die Rotationsenergie des Bretts ergänzen. |
Vielen Dank für die ausführliche Antwort! Wo käme denn die Rotationsenergie des Bretts ins Spiel?
Und was genau bedeutet a_l genau im Kontext? |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 14. Jun 2021 17:58 Titel: Mathefix Verfasst am: 14. Jun 2021 17:58 Titel: |
 |
|
Beim Kippen rotiert das Brett um das Auflager.
a_l ist die Beschleunigung der linken Kugel.
Zuletzt bearbeitet von Mathefix am 15. Jun 2021 09:55, insgesamt 2-mal bearbeitet |
|
 |
Marietra
Anmeldungsdatum: 12.06.2021
Beiträge: 4
|
 Marietra Verfasst am: 14. Jun 2021 21:06 Titel: Marietra Verfasst am: 14. Jun 2021 21:06 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: |


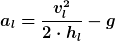 |
Kannst du nochmal erklären, wie die Formeln für h_l, v_l und a_l am Ende zustande kommen? |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 15. Jun 2021 10:45 Titel: Mathefix Verfasst am: 15. Jun 2021 10:45 Titel: |
 |
|
Ansatz unter Berücksichtigung der Masse der Wippe und Vermeidung des Aufpralls der Wippe auf den Boden durch Bestimmung der Auflagerhöhe.
Die fett gedruckten Angaben sind gegeben.
m_r = Masse der fallenden rechten Kugel
m_l = Masse der linken Kugel auf der Wippe
I_l = Massenträgheitsmoment der linken Kugel
h_0 = Fallhöhe m_r über h_r
h_l = Höhe der linken Kante der Wippe beim Abwurf von m_l
h_r = Höhe der rechten Kante der Wippe über dem Boden beim Auftreffen von m_r
mü = 0,4 Reibkoeffizient Kugel Metall/Wippe Holz
L = Länge der Wippe
d = Dicke der Wippe
m_w = Masse der Wippe
I_w = Massenträgheitsmomen der Wippe
l = Abstand des Auflagers von der linken Kante der Wippe
s = Abstand des Massenschwerpunkts der Wippe vom Auflager
h_a = Höhe des Auflagers
omega = Wingelgeschwindigkeit der Wippe
v_l = Abwurfgeschwindigkeit m_l
a_l = Beschleunigung der Masse m_l
Potentielle Energie = Rotationsenergie
=\frac{1}{2}\cdot (I_l+ I_w)\cdot \omega^{2} )
}{I_l + I_w} } )
Bezugsachse Auflager
Massenträgheitsmoment der linken Kugel

Masenträgheitsmoment der Wippe
)

Berechnung h_r und h_a
Ab einem Neigungswinkel = 21,8° ) rutscht m_r von/auf der Wippe. Damit beträgt der Maximalwert von h_r rutscht m_r von/auf der Wippe. Damit beträgt der Maximalwert von h_r
\cdot \sin(\alpha))
Bedingung für die Höhe des Auflagers, damit die Wippe nicht aufschlägt
\cdot \sin(\alpha))
Abwurfgeschwindigkeit der Kugel m_l

}{I_l + I_w} } )
Die Kugel verlässt die Wippe mit v_l in der Höhe h_l/2 + h_a unter dem Winkel beta = 90 - alpha zur waagerechten. Damit kann die Bahnkurve ermittelt werden.
Beschleunigung der Masse m_l
Gleichmässig beschleunigte Bewegung
)
Um diese Höhe wird die Masse m_l angehoben und auf die Geschwindigkeit v_l beschleunigt.


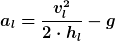
Wenn Du möchtest, kann ich ein Beispiel rechnen.
Zuletzt bearbeitet von Mathefix am 18. Jun 2021 14:07, insgesamt 18-mal bearbeitet |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 15. Jun 2021 14:13 Titel: Mathefix Verfasst am: 15. Jun 2021 14:13 Titel: |
 |
|
| Marietra hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: |


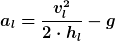 |
Kannst du nochmal erklären, wie die Formeln für h_l, v_l und a_l am Ende zustande kommen? |
Es handelt sich um die Formeln für eine gleichmässig beschleunigte vertikale Bewegung:
Definition Geschwindigkeit

Definition Geschwindigkeit bei konstanter Beschleunigung

Zurückgelegter Weg




Beschleunigung, wenn ein gegebener Weg mit gegebener Geschwindigkeit zurückgelegt wird.

Gegen diese nach oben gerichteten Beschleunigung wirkt die Erdbeschleunigung -g |
|
 |
Marietra
Anmeldungsdatum: 12.06.2021
Beiträge: 4
|
 Marietra Verfasst am: 17. Jun 2021 11:05 Titel: Marietra Verfasst am: 17. Jun 2021 11:05 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: |
Potentielle Energie = Rotationsenergie
=\frac{1}{2}\cdot (I_l+ I_w)\cdot \omega^{2} )
}{I_l + I_w} } )
|
Habe ich das richtig verstanden, dass omega die Geschwindigkeit ist, mit der die Wippe kippt? Oder ist das was anderes? Die Kippgeschwindigkeit ist für mein Modell nämlich auch sehr wichtig.
Und ja, es wäre sehr nett, wenn du ein Beispiel rechnen könntest :) |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 17. Jun 2021 12:57 Titel: Mathefix Verfasst am: 17. Jun 2021 12:57 Titel: |
 |
|
onega ist die Winkelgeschwindigkeit mit der die Wippe um das Auflager rotiert
Beispielrechnung
Gegeben:
m_r = 0,5 kg
m_l = 0,2 kg
h_0 = 1m
mü = 0,4(Metall/Holz)
L = 0,5 m
d = 0,01 m
b = 0,05 m (Breite der Wippe)
m_w = 0,1kg
l = 0,2m
a) Fall mit Reibung
}{I_l + I_w} } )
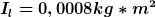
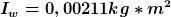






b) Geometrische Lösung
Die fallende Kugel m_r verlässt die Wippe an dem Punkt an dem die senkrechte Falllinie den Kreis mit dem Radius L-l schneidet.
Gegeben.
wie a) ohne mü
h_a = 0,114 m (aus a) übernommen)
)

Um diesen Betrag muss der Boden rechts vom Auflager abgesenkt werden, damit die rechte Kante der Wippe nicht auf den Boden aufschlägt.
 )



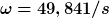


Rechenfehler vorbehalten
Zuletzt bearbeitet von Mathefix am 18. Jun 2021 14:05, insgesamt einmal bearbeitet |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 17. Jun 2021 16:37 Titel: DrStupid Verfasst am: 17. Jun 2021 16:37 Titel: |
 |
|
Ich habe das Ganze mal als vollständig elastischen Stoß aufgefasst und vereinfachend angenommen, dass die Wippe zuächst horizontal liegt und am Schwerpunkt gelagert ist. Dann gilt für die Energie

mit
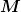 = Masse der fallenden Kugel = Masse der fallenden Kugel
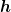 = Fallhöhe = Fallhöhe
 = Aufprallgeschwindigkeit = Aufprallgeschwindigkeit
 = Geschwindigkeit der fallenden Kugel nach dem Stoß = Geschwindigkeit der fallenden Kugel nach dem Stoß
 = Geschwindigkeit der hochgeworfenen Kugel nach dem Stoß = Geschwindigkeit der hochgeworfenen Kugel nach dem Stoß
 = Winkelgeschwindigkeit der Wippe nach dem Stoß = Winkelgeschwindigkeit der Wippe nach dem Stoß
 = Trägheitsmoment der Wippe = Trägheitsmoment der Wippe
Für den Drehimpuls gilt

mit
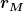 = Abstand der herunterfallenden Kugel vom Lager der Wippe = Abstand der herunterfallenden Kugel vom Lager der Wippe
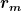 = Abstand der hochgeworfenen Kugel vom Lager der Wippe = Abstand der hochgeworfenen Kugel vom Lager der Wippe
Außerdem gehe ich davon aus, dass die hochgeworfene Kugel sich unmittelbar nach dem Stoß so schnell bewegt, wie die Stelle der Wippe auf der sie liegt:

Nach Substitution mit

)
ergibt das

Wenn das so OK ist, dann könnte man das erweitern, indem die Wippe nicht am Schwerpunkt gelagert ist (das ist relativ einfach) oder beim Aufprall nicht horizontal liegt (das wird komplizierter, weil das Problem dann nicht mehr eindimensional ist). |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 17. Jun 2021 17:07 Titel: Mathefix Verfasst am: 17. Jun 2021 17:07 Titel: |
 |
|
@DrStupid
Wie kann die im Schwerpunkt gelagerte Wippe horizontal liegen, wenn auf einer Seite die hochzuschleudernde Kugel liegt?
Ich habe unterstellt, dass die Wippe
a) geneigt ist. Die Kante auf der die Kugel liegt berührt den Boden.
b) nicht im Schwerpunkt gelagert ist
c) nicht auf den Boden aufprallt. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 17. Jun 2021 18:26 Titel: DrStupid Verfasst am: 17. Jun 2021 18:26 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | | Wie kann die im Schwerpunkt gelagerte Wippe horizontal liegen, wenn auf einer Seite die hochzuschleudernde Kugel liegt? |
Einfaches Beispiel: Lineal mit Schwerpunkt auf der Tischkante.
| Mathefix hat Folgendes geschrieben: | Ich habe unterstellt, dass die Wippe
a) geneigt ist. Die Kante auf der die Kugel liegt berührt den Boden.
b) nicht im Schwerpunkt gelagert ist
c) nicht auf den Boden aufprallt. |
Damit werde ich es auch mal durchrechnen. Aber wie ich schon sagte, wird das deutlich komplizierter. |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 18. Jun 2021 09:29 Titel: Mathefix Verfasst am: 18. Jun 2021 09:29 Titel: |
 |
|
@DrStupid
| DrStupid hat Folgendes geschrieben: | Dann gilt für die Energie
 |
Da m bis zum Abwurf gemeinsam mit der Wippe eine Rotationsbewegung ausführt, muss dann nicht der Term für die kinetische Energie von m statt
der translatorischen Energie

die Rotationsenergie

angesetzt werden?
Für J_m gilt dann Steiner.
Gruss
Mathefix
Zuletzt bearbeitet von Mathefix am 18. Jun 2021 09:48, insgesamt einmal bearbeitet |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 18. Jun 2021 09:46 Titel: DrStupid Verfasst am: 18. Jun 2021 09:46 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | Da m bis zum Abwurf gemeinsam mit der Wippe eine Rotationsbewegung ausführt, muss dann nicht der Term für die kinetische Energie von m statt der translatorischen Energie

die Rotationsenergie

angesetzt werden? |
Das ist dasselbe. |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 18. Jun 2021 10:01 Titel: Mathefix Verfasst am: 18. Jun 2021 10:01 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | Da m bis zum Abwurf gemeinsam mit der Wippe eine Rotationsbewegung ausführt, muss dann nicht der Term für die kinetische Energie von m statt der translatorischen Energie

die Rotationsenergie

angesetzt werden? |
Das ist dasselbe. |
Aber nur, wenn m als Punktmasse definiert wird. J_m = m * r_m^2
Zuletzt bearbeitet von Mathefix am 18. Jun 2021 10:29, insgesamt 3-mal bearbeitet |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 18. Jun 2021 10:17 Titel: DrStupid Verfasst am: 18. Jun 2021 10:17 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | | Aber nur, wenn m als Punktmasse definiert wird. J_m = m * r_m^2 |
Nein, das gilt auch auch wenn m eine Kugel ist. Die Normalkraft, die die Kugel beschleunigt, geht direkt durch ihren Masseschwerpunkt. Das bedeutet, dass die Kugel nicht in Rotation um ihren Schwerpunkt versetzt wird. Ihre Rotationsenergie im oben gewählten Bezugssystem besteht damit nur aus der kinetischen Energie ihres Masseschwerpunktes.
Bei einer schräg stehenden Wippe könnte das durchaus anders aussehen. Aber auch da würde ich vereinfachende Annahmen machen, die dazu führen, dass die Kugel nicht um ihren Schwerpunkt rotiert. Andernfalls müsste man nämlich auch noch die Reibung zwischen Kugel und Wippe berücksichtigen. |
|
 |
|















