| Autor |
Nachricht |
Schneller Hase
Gast
|
 Schneller Hase Verfasst am: 09. März 2021 14:19 Titel: 2 Elektronen in 3D harm. Osz. Störungstheorie Schneller Hase Verfasst am: 09. März 2021 14:19 Titel: 2 Elektronen in 3D harm. Osz. Störungstheorie |
 |
|
Meine Frage:
Hallo. (ANMERKUNG: Ich erkläre alles, was ich gemacht habe, bevor ich auf das Problem, bei dem ich nicht weitergekommen bin, gestoßen bin, die eigentliche Frage ist, wie ich ein bestimmtes Integral berechnen kann (siehe unten), deswegen könnt ihr auch gerne den ganzen vorderen Teil überspringen, wenn euch das ganze zu lang ist, ansonsten freue ich mich natürlich, wenn auch über meinen Anfang kurz drübergeschaut wird  ) )
Folgendes Problem:
Zwei Elektronen befinden sich in einem EInteilchenpotential (gegeben durch dreidimensionalen, isotropen harmonischen Oszillator mit fester Frequenz  ). Zunächst sollte man die Energie und Eigenfunktion des Grundzustands bestimmen und zwar mit Orts- und Spinkomponenten, wenn man die Elektron-Elektron Wechselwirkung vernachlässigt. ). Zunächst sollte man die Energie und Eigenfunktion des Grundzustands bestimmen und zwar mit Orts- und Spinkomponenten, wenn man die Elektron-Elektron Wechselwirkung vernachlässigt.
Das habe ich geschafft:
Hamiltonoperator:

Definiere als zwei Einteilchen Hamiltonoperatoren:


Grundzustandswellenfunktion des eindimensionalen harmonischen Oszillators:
=\frac{1}{\sqrt{\eta\sqrt{\pi}}} e^{-\frac{x^2}{2\eta^2} })
mit

Damit bekommt man leicht die Einteilchenwellenfunktion für den dreidimensionalen harmonischen Oszillator:
=\frac{1}{\sqrt{\eta\sqrt{\pi}}} e^{-\frac{x^2+y^2+z^2}{2\eta^2} }=\frac{1}{\sqrt{\eta\sqrt{\pi}}} e^{-\frac{r^2}{2\eta^2} })
Da Elektronen Fermionen sind, muss meine Gesamtwellenfunktion ja antisymmetrisch sein. Ich will aber gleichzeitig den Grundzustand haben. Die niedrigste Energien bekomme ich, wenn beide Elektronen die Grundzustandsortswellenfunktion besitzen, die ich oben hergeleitet habe. Das beduetet aber, das ihre Spins nicht parallel ausgerichtet sein können aufgrund des Pauli Prinzips. Der Gesamtspin meiner zwei Elektronen ist daher 0 und somit auch die Gesamtmagnetquantenzahl.
Es gilt somit:

Und damit muss die Spinkomponente der Wellenfunktion gerade der des Paraheliums entsprechen, während die Ortskomponente einfach das Produkt der beiden Einteilchen-Wellenfunktionen sein sollte, die Normierung sollte ja schon richtig sein.
Meine Eigenfunktion des Grundzustands:
=\phi(r_1,r_2)\chi)
mit Ortskomponente:
=\frac{1}{\eta\sqrt{\pi}}e^{-\frac{r_{1}^2+r_{2}^2}{2\eta^2} })
und Spinkomponente:

Bleibt die Energie des Grundzustandes zu bestimmen. Das ist einfach, da die beiden Einteilchen Hamiltonoperatoren, in die ich meinen Hamiltonoperator aufgeteilt habe, nicht auf die Spinkomponente wirken, meine Energie ist also die Summe der beiden Energien zweier Einteilchen Oszillatoren:
)
da beide im Grundzustand sind, sind alle 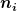
gleich 0 und somit ist die Gesamtenergie des Grundzustandes:

Ist bis hierhin alles in Ordnung?
Jetzt komme ich zu dem Teil der Aufgabe, in dem mein Problem liegt:
Berechne mit Hilfe von Stöungstheorie 1. Ordnung, wie sich die Grundzustandsenergie aufgrund der Elektron-Elektron-Wechselwirkung ändert.
Meine Ideen:
Hierfür habe ich den Hamiltonoperator nochmals angepasst:

mit


Die Abweichung von der Grundzustandsenergie ohne die kleine Störung (hier der Wechselwirkungsterm zwischen den Elektronen) ergibt sich nach der Störungstheorie 1. Ordnung zu:
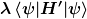
Ich muss also im Wesentlichen folgendes Integral lösen:

Die Vorfaktoren habe ich hier erstmal weggelassen.
Laut der Angabe gilt folgender Trick:
}{|\vec{r}_1-\vec{r}_2|} = \int \! \dd^3 r_1 \, \int \! \dd^3 r_2 \, \frac{f(|r_1|,|r_2|)}{max(|r_1|,|r_2|)} )
Wenn ich diesen Trick auf mein zu lösendes Integral anwende und die Winkelintegrale direkt rausziehe (beide zusammen sollten einen Vorfaktor von  ergeben, da ich zweimal ergeben, da ich zweimal 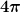 erhalte durch das jeweilige Integral über Phi und sin(Theta), erhalte ich folgendes Integral zum Lösen: erhalte durch das jeweilige Integral über Phi und sin(Theta), erhalte ich folgendes Integral zum Lösen:
} )
Und hier liegt mein Problem, weil ich nicht weiß, wie ich hier mit dem Maximum umgehen soll.
Ich hatte bereits zwei Wege probiert, einmal hatte ich einfach angenommen, dass 
Dabei bin ich mir aber nicht sicher, ob dieses Vorgehen gerechtfertigt ist, da ich ja beide  von 0 bis unendlich laufen lasse. von 0 bis unendlich laufen lasse.
Meine zweite Idee war, 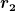 zunächst bis zunächst bis 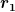 integriert und dieses dann von 0 bis unendlich. Das hat aber den Nachteil, dass das Integral dann nicht lösbar ist, da es ja ein Gaußintegral ist. Daher scheint dieser Ansatz auch falsch zu sein. integriert und dieses dann von 0 bis unendlich. Das hat aber den Nachteil, dass das Integral dann nicht lösbar ist, da es ja ein Gaußintegral ist. Daher scheint dieser Ansatz auch falsch zu sein.
DAHER MEINE ABSCHLIEßENDE FRAGE:
Wie kann ich dieses Integral lösen und wie muss ich dabei mit dem Maximum umgehen?
Ich weiß leider nicht mehr weiter.
Danke im Voraus! |
|
 |
gast_0221
Gast
|
 gast_0221 Verfasst am: 09. März 2021 14:38 Titel: gast_0221 Verfasst am: 09. März 2021 14:38 Titel: |
 |
|
| Zitat: | | Meine zweite Idee war, zunächst bis integriert und dieses dann von 0 bis unendlich. |
Der Integrant ist unabhängig vom Winkelanteil, wo ist das Problem?
Einfach  setzten. setzten. |
|
 |
Schneller Hase
Gast
|
 Schneller Hase Verfasst am: 09. März 2021 14:52 Titel: Schneller Hase Verfasst am: 09. März 2021 14:52 Titel: |
 |
|
| gast_0221 hat Folgendes geschrieben: | | Zitat: | | Meine zweite Idee war, zunächst bis integriert und dieses dann von 0 bis unendlich. |
Der Integrant ist unabhängig vom Winkelanteil, wo ist das Problem?
Einfach  setzten. setzten. |
Also darf ich tatsächlich einfach eine der beiden Variablen als "größer als die andere Variable" setzen? Genau da war ich mir eben nicht sicher. Ist das dann erlaubt, weil die beiden Elektronen ununterscheidbar sind? Weil es ist doch nicht gesagt, dass r_1 immer größer als r_2 ist? |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 09. März 2021 16:32 Titel: jh8979 Verfasst am: 09. März 2021 16:32 Titel: |
 |
|
Interessanter Trick mit dem Max. Den hab ich noch nie gesehen (und seh gerade auch nicht wieso er gilt, aber das nur nebenbei).
1. In Deinem Integral über r1 und r2 fehlen noch ein verschiedene r^2-Terme die vom Volumenmaß stammen.
2. Du kannst natürlich nicht so einfach dein Max durch eines der beiden Argumente ersetzen. Aber Du kannst Deine Integrationsbereiche so aufteilen, dass Du in jedem das Max entsprechend ersetzen kannst. |
|
 |
Schneller Hase
Gast
|
 Schneller Hase Verfasst am: 09. März 2021 16:54 Titel: Schneller Hase Verfasst am: 09. März 2021 16:54 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | Interessanter Trick mit dem Max. Den hab ich noch nie gesehen (und seh gerade auch nicht wieso er gilt, aber das nur nebenbei).
1. In Deinem Integral über r1 und r2 fehlen noch ein verschiedene r^2-Terme die vom Volumenmaß stammen.
2. Du kannst natürlich nicht so einfach dein Max durch eines der beiden Argumente ersetzen. Aber Du kannst Deine Integrationsbereiche so aufteilen, dass Du in jedem das Max entsprechend ersetzen kannst. |
Zu 1. Ja, da ist meine Schreibweise etwas blöd, also ich hab den r^2 Teil nicht vergessen, aber es verwirrend hingeschrieben.
Zu 2. das habe ich vermutet, als ich meinen Versuch gemacht habe, das eine Integral bis zum Wert der anderen Variable zu integrieren und diese dann von 0 bis unendlich, aber der Ansatz ist gescheitert, da ich ja dann eine errorfunction bekomme. Wie müsste ich die Integrationsbereichedenn da aufteilen? Das ist nämlich genau das, was ich gestern versucht habe, aber nicht zufriedenstellend (meiner Meinung nach) hinbekommen habe.
Ich hätte grad spontan noch diese Idee, das so aufzuteilen:
)
Aber bekomme ich dann nicht wieder mit der errorfunction Probleme beim berechnen? |
|
 |
Schneller Hase
Gast
|
 Schneller Hase Verfasst am: 09. März 2021 17:47 Titel: Schneller Hase Verfasst am: 09. März 2021 17:47 Titel: |
 |
|
|
Hab jetzt die Idee von mir durchgerechnet, da bleibt am Ende wieder eine errorfunction übrig über die ich nochmal integrieren müsste, irgendwas mache ich wohl falsch. |
|
 |
gast_0221
Gast
|
 gast_0221 Verfasst am: 09. März 2021 18:11 Titel: gast_0221 Verfasst am: 09. März 2021 18:11 Titel: |
 |
|
Bei  Kettenregel anwenden bzw. substituieren und bei Kettenregel anwenden bzw. substituieren und bei  kann man vorher partiell Integriegen. Hab das jetzt nicht durchgerechnet aber der Integrand kann am Ende eingentlich kein reiner Exponentialausdruck sein. kann man vorher partiell Integriegen. Hab das jetzt nicht durchgerechnet aber der Integrand kann am Ende eingentlich kein reiner Exponentialausdruck sein. |
|
 |
Schneller Hase
Gast
|
 Schneller Hase Verfasst am: 09. März 2021 18:17 Titel: Schneller Hase Verfasst am: 09. März 2021 18:17 Titel: |
 |
|
Ich habs aber genau ausgerechnet und es ist so 
das integral von r1 bis unendlich ist leicht zu berechnen wie du schon sagtest und beim anderen Integral, auch, wie du gesagt hast, erst einmal partielle integration. Der erste term der PI und der term vom r1 bis unendlich integral addieren sich zu 0. Beim anderen Integral hab ich 2r_2 durch die Ableitung dieses r Terms und noch n^2/r_2 durch die "Aufleitung" der exp funktion bei der partiellen integration, dadurch fällt das r_2 raus und ich habe eine errorfunction da stehen. Außer ich hätte mich komplett verrechnet, aber das glaub ich nicht, da ich die rechnung eigentlich mit 2 computerprogrammen zusätzlich zur händischen rechnung überprüft habe. |
|
 |
gast_0221
Gast
|
 gast_0221 Verfasst am: 09. März 2021 18:30 Titel: gast_0221 Verfasst am: 09. März 2021 18:30 Titel: |
 |
|
| gast_0221 hat Folgendes geschrieben: | | der Integrand kann am Ende eingentlich kein reiner Exponentialausdruck sein. |
Korrektur: schon, aber es wird ja über alle positiven Reellen zahlen integriert und es ist ja

| Zitat: | | 2r_2 durch die Ableitung dieses r Terms |
Woher? Bei partieller Integration von  ) müsstest du den geklammerten Ausdruck integrieren und r ableiten (->1 ) müsstest du den geklammerten Ausdruck integrieren und r ableiten (->1 ) |
|
 |
Schneller Hase
Gast
|
 Schneller Hase Verfasst am: 09. März 2021 18:37 Titel: Schneller Hase Verfasst am: 09. März 2021 18:37 Titel: |
 |
|
| gast_0221 hat Folgendes geschrieben: | | gast_0221 hat Folgendes geschrieben: | | der Integrand kann am Ende eingentlich kein reiner Exponentialausdruck sein. |
Korrektur: schon, aber es wird ja über alle positiven Reellen zahlen integriert und es ist ja

| Zitat: | | 2r_2 durch die Ableitung dieses r Terms |
Woher? Bei partieller Integration von  ) müsstest du den geklammerten Ausdruck integrieren und r ableiten (->1 ) müsstest du den geklammerten Ausdruck integrieren und r ableiten (->1 ) |
Zum zweiten: Ich hab r^2 als einen Term und die e-Funktion als den anderen term genommen bei der PI. Und es wird in dem betreffenden Integral eben NICHT über alle positiven reellen Zahlen integriert, sondern nur bis r_1, weil sonst ändert sich der nenner durch die definition des macimalwertes im Nenner |
|
 |
gast_0221
Gast
|
 gast_0221 Verfasst am: 09. März 2021 18:51 Titel: gast_0221 Verfasst am: 09. März 2021 18:51 Titel: |
 |
|
Ich will nochmal kurz anmerken dass ich den Ansatz nicht durchgecheckt habe aber was Integral angeht:
| Schneller Hase hat Folgendes geschrieben: | | Ich hab r^2 als einen Term und die e-Funktion als den anderen term genommen bei der PI |
Zu  lässt sich aber keine analytische Stammfunktion hinschreiben. Bei der partiellen Integration ist es deshalb geschickter, direkt die Stammfunktion des Ausdrucks der Form lässt sich aber keine analytische Stammfunktion hinschreiben. Bei der partiellen Integration ist es deshalb geschickter, direkt die Stammfunktion des Ausdrucks der Form  zu benutzen. zu benutzen. |
|
 |
Schneller Hase
Gast
|
 Schneller Hase Verfasst am: 09. März 2021 18:57 Titel: Schneller Hase Verfasst am: 09. März 2021 18:57 Titel: |
 |
|
| gast_0221 hat Folgendes geschrieben: | Ich will nochmal kurz anmerken dass ich den Ansatz nicht durchgecheckt habe aber was Integral angeht:
| Schneller Hase hat Folgendes geschrieben: | | Ich hab r^2 als einen Term und die e-Funktion als den anderen term genommen bei der PI |
Zu  lässt sich aber keine analytische Stammfunktion hinschreiben. Bei der partiellen Integration ist es deshalb geschickter, direkt die Stammfunktion des Ausdrucks der Form lässt sich aber keine analytische Stammfunktion hinschreiben. Bei der partiellen Integration ist es deshalb geschickter, direkt die Stammfunktion des Ausdrucks der Form  zu benutzen. zu benutzen. |
Das mag sein, es kommt bei deinem Weg aber das selbe raus wie bei meinem (leider) hab ich Grad nachgeprüft. Also bis auf einen irrelevanten Vorfaktor kommt das selbe raus. |
|
 |
|
|
















 )
)
