| Autor |
Nachricht |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
 Corbi Verfasst am: 28. Okt 2020 11:48 Titel: Abstandsbestimmung in der ART Corbi Verfasst am: 28. Okt 2020 11:48 Titel: Abstandsbestimmung in der ART |
 |
|
Um ein Eigenzeitintervall in der ART zu bestimmen, setzt man einfach das räumliche Wegelement  und erhält damit: und erhält damit:

In Landau/Lifschitz II steht, dass man um den räumlichen Abstand 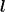 zu bestimmen ( der definiert ist als der Raumzeit-Abstand zu bestimmen ( der definiert ist als der Raumzeit-Abstand 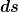 zu ein und der selben Zeit) nicht einfach zu ein und der selben Zeit) nicht einfach 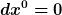 einsetzen kann. einsetzen kann.
Kann mir das bitte jemand genauer erklären. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 28. Okt 2020 18:59 Titel: Re: Abstandsbestimmung in der ART index_razor Verfasst am: 28. Okt 2020 18:59 Titel: Re: Abstandsbestimmung in der ART |
 |
|
| Corbi hat Folgendes geschrieben: | Um ein Eigenzeitintervall in der ART zu bestimmen, setzt man einfach das räumliche Wegelement  und erhält damit: und erhält damit:

|
Das ist so nicht ganz richtig. Zu jeder zeitartigen Weltlinie gehört ein Eigenzeitintervall. Es spielt keine Rolle ob diese Weltlinie parallel zu einer Koordinate 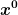 verläuft. Das ganze hat also mit einem "räumlichen Wegelement" erstmal gar nichts zu tun. verläuft. Das ganze hat also mit einem "räumlichen Wegelement" erstmal gar nichts zu tun.
| Zitat: |
In Landau/Lifschitz II steht, dass man um den räumlichen Abstand 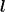 zu bestimmen ( der definiert ist als der Raumzeit-Abstand zu bestimmen ( der definiert ist als der Raumzeit-Abstand 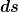 zu ein und der selben Zeit) nicht einfach zu ein und der selben Zeit) nicht einfach 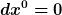 einsetzen kann. einsetzen kann.
Kann mir das bitte jemand genauer erklären. |
Um den räumlichen Abstand zu einem Ereignis x zu definieren, muß man zuerst eine Menge von Ereignissen festlegen, die für einen bestimmten Beobachter gleichzeitig zu x stattfinden. Alles was man dazu zur Verfügung hat, ist die Eigenzeit des Beobachters und Lichtsignale: gleichzeitig zu x sind solche Ereignisse y, deren Rückwärtslichtkegel die Weltlinie in einem Ereignis schneidet, das genauso lange vor x stattfindet, wie der Schnittpunkt mit dem Vorwärtslichtkegel von y nach x, jeweils gemessen in der Eigenzeit des Beobachters. Wenn sich aus solchen Ereignissen y eine raumartige Hyperfläche bilden läßt, dann ist deren räumliche Metrik bis aufs Vorzeichen die Einschränkung der Minkowskimetrik auf Tangentialvektoren an diese Fläche.
Das ist im wesentlichen die Konstruktion von Landau, Lifshitz. Sie wählen zwar ein spezielles Koordinatensystem, in welchem 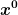 parallel zur Weltlinie verläuft. Aber außer, daß parallel zur Weltlinie verläuft. Aber außer, daß  sein muß -- ansonsten definiert sein muß -- ansonsten definiert 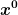 keine zeitartige Weltlinie -- hat dieses Koordinatensystem keine physikalische Bedeutung. Das gilt insbesondere für die Bedingung keine zeitartige Weltlinie -- hat dieses Koordinatensystem keine physikalische Bedeutung. Das gilt insbesondere für die Bedingung  . . |
|
 |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
 Corbi Verfasst am: 29. Okt 2020 15:33 Titel: Re: Abstandsbestimmung in der ART Corbi Verfasst am: 29. Okt 2020 15:33 Titel: Re: Abstandsbestimmung in der ART |
 |
|
okay also ich glaube den ersten Punkt zu verstehen und die Konstruktion des metrischen des Tensors des Raums im Landau kann ich auch nachvollziehen.
Aber kann ich nicht auch einfach folgendes tun:
Wenn man z.B. die Schwarzschildmetrik hat:
dx^{02}+(\frac{1}{1-r_S/r})dr^2+r^2d\theta^2 +r^2\sin{\theta}^2d\phi^2 )
kann ich dann den räumlichen Abstand zwischen zwei Punkten nicht einfach bestimmen indem ich dx^0=0 setze und dann erhalte:
dr^2+r^2d\theta^2 +r^2\sin{\theta}^2d\phi^2 ) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 29. Okt 2020 16:35 Titel: Re: Abstandsbestimmung in der ART index_razor Verfasst am: 29. Okt 2020 16:35 Titel: Re: Abstandsbestimmung in der ART |
 |
|
| Corbi hat Folgendes geschrieben: |
Aber kann ich nicht auch einfach folgendes tun:
Wenn man z.B. die Schwarzschildmetrik hat:
dx^{02}+(\frac{1}{1-r_S/r})dr^2+r^2d\theta^2 +r^2\sin{\theta}^2d\phi^2 )
kann ich dann den räumlichen Abstand zwischen zwei Punkten nicht einfach bestimmen indem ich dx^0=0 setze und dann erhalte:
dr^2+r^2d\theta^2 +r^2\sin{\theta}^2d\phi^2 ) |
Da in diesem Fall alle  läuft das natürlich auf dasselbe hinaus. Die Existenz solcher Koordinaten ist eine Spezialität von statischen Gravitationsfeldern. Tatsächlich ist dieses läuft das natürlich auf dasselbe hinaus. Die Existenz solcher Koordinaten ist eine Spezialität von statischen Gravitationsfeldern. Tatsächlich ist dieses  die räumliche Metrik eines ruhenden Beobachters in der Schwarzschildmetrik. Im Gravitationsfeld rotierender Körper oder lediglich in einem anderen Koordinatensystem für die Schwarzschildmetrik funktioniert das nicht mehr so einfach. Siehe dazu auch § 88 in Landau, Lifschitz. die räumliche Metrik eines ruhenden Beobachters in der Schwarzschildmetrik. Im Gravitationsfeld rotierender Körper oder lediglich in einem anderen Koordinatensystem für die Schwarzschildmetrik funktioniert das nicht mehr so einfach. Siehe dazu auch § 88 in Landau, Lifschitz. |
|
 |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
 Corbi Verfasst am: 29. Okt 2020 19:26 Titel: Corbi Verfasst am: 29. Okt 2020 19:26 Titel: |
 |
|
okay soweit klar.
Bei §89 wird dann die räumliche Metrik eines rotierenden Beobachters in einer flachen Raumzeit betrachtet.
Dazu habe ich noch eine Verständnisfrage:
Die 3D-Untermannigfaltigkeit nimmt für den rotierenden Beobachter eine nichteuklidische Geometrie an.
Die Raumzeit-Metrik dieses rotierenden Beobachters muss ja immernoch eine flache Geometrie beschreiben, da sich die geometrische Struktur durch eine Koordinatentransformation ja nicht ändern kann.
Sehe ich das so richtig? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 30. Okt 2020 07:53 Titel: index_razor Verfasst am: 30. Okt 2020 07:53 Titel: |
 |
|
| Corbi hat Folgendes geschrieben: |
Bei §89 wird dann die räumliche Metrik eines rotierenden Beobachters in einer flachen Raumzeit betrachtet.
Dazu habe ich noch eine Verständnisfrage:
Die 3D-Untermannigfaltigkeit nimmt für den rotierenden Beobachter eine nichteuklidische Geometrie an.
Die Raumzeit-Metrik dieses rotierenden Beobachters muss ja immernoch eine flache Geometrie beschreiben, da sich die geometrische Struktur durch eine Koordinatentransformation ja nicht ändern kann.
Sehe ich das so richtig? |
Ja, im Prinzip stimmt das wohl.
Die Raumzeitmetrik ist von Beobachter und Koordinaten unabhängig, also ist sie für alle Beobachter fach, wenn sie es für einen ist. Ich würde allerdings aus diesem Grund auch nicht von der "Raumzeitmetrik dieses Beobachters" sprechen. Die Raumzeitmetrik gehört einfach zur Raumzeit. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18030
|
 TomS Verfasst am: 30. Okt 2020 09:19 Titel: TomS Verfasst am: 30. Okt 2020 09:19 Titel: |
 |
|
[quote="index_razor"] | Corbi hat Folgendes geschrieben: |
Ich würde allerdings aus diesem Grund auch nicht von der "Raumzeitmetrik dieses Beobachters" sprechen. Die Raumzeitmetrik gehört einfach zur Raumzeit. |
Genau.
Ergänzung:
Zunächst mal ist die Raumzeitmetrik g eine Bilinearform, die zwei Vektoren x,y (koordinatenfrei!) auf einen Skalar g(x,y) abbildet. Insofern ist sie koordinaten- und beobachterunabhängig.
Dann gibt es die aus der SRT übernommene Unsitte, Koordinatensysteme mit Bezugsystemen von Beobachtern gleichzusetzen. Das trifft in der ART jedoch i.A. nicht zu; man kann durchaus Koordinatensysteme betrachten, ohne dass es dazu einen physikalisch sinnvollen Beobachter geben muss.
Und zuletzt ist dies auch extrem irreführend. Betrachtet man z.B. ein Photon mit 4er-Wellenvektor k und einen Beobachter mit 4er-Geschwindigkeit u, so ist die Frequenz omega des Photons, die der Beobachter wahrnimmt, gegeben durch
 = g(u,k) = g_{\mu\nu} \, u^\mu \, k^\nu)
Erst die rechte Seite verwendet konkrete Koordinaten; diese haben jedoch nichts mit dem Ruhesystem des Beobachters zu tun.
Diese Frequenz omega ist ein Skalar, sie ist koordinatensystemubabhängig. Allerdings ist sie nicht beobachterunabhängig, denn eine Änderung von u führt zu einem anderen Wert von omega (Dopplereffekt).
Man muss zwischen dem Wechsel des Koordinatensystems und dem Wechsel des Beobachters unterscheiden. Leider ist der Sprachgebrauch in vielen einführenden Darstellungen der SRT da ziemlich schlampig.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Corbi
Anmeldungsdatum: 17.07.2018
Beiträge: 296
|
 Corbi Verfasst am: 30. Okt 2020 10:36 Titel: Corbi Verfasst am: 30. Okt 2020 10:36 Titel: |
 |
|
ok! Vielen Dank!
| Zitat: | | Man muss zwischen dem Wechsel des Koordinatensystems und dem Wechsel des Beobachters unterscheiden. Leider ist der Sprachgebrauch in vielen einführenden Darstellungen der SRT da ziemlich schlampig. |
Ja das hat mich in der Tat von Anfang an in der ART verwirrt. Danke für den hilfreichen Beitrag.
Irgendwie finde ich da schon die Namensgebung "Spezielle Relativitätstheorie" und "Allgemeine Relativitätstheorie" sehr irreführend. Das Grundprinzip, der speziellen Relativitätstheorie, dass die Physik für alle inertialen Beobachter diesselbe ist, wird ja nicht wirklich auf beliebig bewegte Beobachter verallgemeinert.
Die Allgemeine Kovarianz in der ART entspricht ja keiner Verallgemeinerung des Speziellen Relativitätsprinzips. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 30. Okt 2020 11:23 Titel: index_razor Verfasst am: 30. Okt 2020 11:23 Titel: |
 |
|
| Corbi hat Folgendes geschrieben: |
| Zitat: | | Man muss zwischen dem Wechsel des Koordinatensystems und dem Wechsel des Beobachters unterscheiden. Leider ist der Sprachgebrauch in vielen einführenden Darstellungen der SRT da ziemlich schlampig. |
Ja das hat mich in der Tat von Anfang an in der ART verwirrt. Danke für den hilfreichen Beitrag.
Irgendwie finde ich da schon die Namensgebung "Spezielle Relativitätstheorie" und "Allgemeine Relativitätstheorie" sehr irreführend. Das Grundprinzip, der speziellen Relativitätstheorie, dass die Physik für alle inertialen Beobachter diesselbe ist, wird ja nicht wirklich auf beliebig bewegte Beobachter verallgemeinert.
Die Allgemeine Kovarianz in der ART entspricht ja keiner Verallgemeinerung des Speziellen Relativitätsprinzips. |
Genau so ist es. Historisch hat es wohl einige Verwirrung um den Begriff "allgemeine Kovarianz" und sein Verhältnis zum Relativitätsprinzip gegeben. Einstein eigener Leitgedanke scheint wohl gewesen zu sein das "spezielle Relativitätsprinzip" auf beliebige Koordinatentransformationen zu verallgemeinern um die Gravitation einzubeziehen.
Allerdings ist die "Invarianz unter allgemeinen Koordinatentransformationen" in der ART keine Verallgemeinerung der Invarianz unter Lorentztransformationen in der SRT. Im Gegenteil, das Relativitätsprinzip ist eine Aussage über die Symmetrie von Bewegungs- und Feldgleichungen. Die Feldgleichungen der ART besitzen aber überhaupt keine Symmetrien (zumindest sind, soweit ich weiß, keine allgemeinen Symmetrien bekannt). Nur spezielle Lösungen der Feldgleichungen haben spezielle Symmetrien, die sich als Isometrien der Metrik manifestieren, wie z.B. die Symmetrie unter der Poincare-Gruppe im Minkowskiraum .
Andererseits hat man bald herausgefunden, daß praktisch alle Theorien "allgemein kovariant" im Sinne der "Invarianz unter beliebigen Koordinatentransformationen" sind. Das gilt sowohl für die Newtonsche Mechanik als auch die spezielle Relativitätstheorie und selbst für Äthertheorien. Alles was man braucht, sind geeignete geometrische Strukturen, mit denen man die Theorie formulieren kann. Die Struktur von Äthertheorien entspricht z.B. im wesentlichen dem Minkowskiraum erweitert um ein paar zusätzliche Felder, z.B. ein zeitartiges Vektorfeld ) auf der gesamten Raumzeit. Damit hat man sofort eine "ausgezeichnete Klasse von Koordinatensystemen" auf der gesamten Raumzeit. Damit hat man sofort eine "ausgezeichnete Klasse von Koordinatensystemen"  = \partial_0, \ \partial_i \perp\partial_0) . Trotzdem sagen die Gleichungen der Theorie dasselbe in jedem Koordinatensystem über die zugrundeliegenden Strukturen, inklusive . Trotzdem sagen die Gleichungen der Theorie dasselbe in jedem Koordinatensystem über die zugrundeliegenden Strukturen, inklusive ) , aus. , aus. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18030
|
 TomS Verfasst am: 30. Okt 2020 12:33 Titel: TomS Verfasst am: 30. Okt 2020 12:33 Titel: |
 |
|
Und um noch eins draufzusetzen kann man die Lorentztransformation als lokale Eichtransfornation auf dem Tangentialbündel einer allgemeinen Riemannschen Mannigfaltigkeit auffassen. Damit wird klar, dass beide - lokale Lorentztransformationen und Diffeomorphismen - nichts miteinander zu tun haben.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|















