| Autor |
Nachricht |
Woelfi
Gast
|
 Woelfi Verfasst am: 01. Okt 2020 13:40 Titel: Vollzylinder verschiedene Rollbahnen |
 |
|
Meine Frage:
Hallo,
ich hoffe ihr könnt mir helfen ich komme leider von allein nicht auf die Lösung.
Also ich habe einen idealen Vollzylinder der eine parabolische Bahn runterrollt. Die Frage ist :Wie sich die Situation ändert wenn die Bahn nicht parabolisch ist sondern linear verläuft.
Meine Ideen:
Ich habe die Lösung dazu. Die Geschwindigkeit ist dieselbe aber die maximale Geschwindigkeit wird später erreicht. Und das ist meine Frage: Wieso wird sie später erreich? Weil die Steigung nicht so stark ist?
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
| Mathefix Verfasst am: 01. Okt 2020 15:17 Titel: |
|
|
Die Endgeschwindigkeiten sind gleich. Unterschiedlich sind die Momentangeschwindigkeiten,
da die Abnahme der potentiellen Energie vom Steigungsverlauf abhängt. Bei der schiefen Ebene ist er konstant, bei der Parabel erst steiler und dann flacher oder umgekehrt je nach Öffnung.
Zuletzt bearbeitet von Mathefix am 01. Okt 2020 15:25, insgesamt einmal bearbeitet |
|
|
Woelfi
Gast
|
| Woelfi Verfasst am: 01. Okt 2020 15:24 Titel: |
|
|
|
Das stimmt die Endgeschwindigkeit ist gleich aber sie soll später als bei der Parabel eintreffen und das genau ist mein Problem, warum ist das so? Weil der Winkel anders ? Also damit meine ich die Parabel ist steiler als die lineare
|
|
|
Woelfi
Gast
|
| Woelfi Verfasst am: 01. Okt 2020 15:27 Titel: |
|
|
|
es geht eigentlich nur um die verschiedenen Bahnen die ein Vollzylinder runtersaust. Es ist einmal eine "halbe Parabel" und dann eben linear wie ein Brett auf dem der Zylinder ist
|
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 01. Okt 2020 16:45 Titel: |
|
|
Für den Anfang kannst du mal überlegen, für welche der folgenden Varianten die Rolle am schnellsten am Ziel ist:
Es gibt einen Höhenunterschied H und eine horizontale Entfernung L=2H.
1. Die Rolle A rollt eine Rampe (Alpha=45°) hinunter und danach weiter eine horizontale Strecke L/2.
2. Die Rolle B rollt eine Rampe tan(Alpha)=0,5 (ca. 26,6°) hinunter.
Beim Zieleinlauf haben beide den gleichen Höhenunterschied überwunden und die gleiche horizontale Entfernung zurückgelegt.
Beide haben die gleiche Endgeschwindigkeit. (E-Erhaltungssatz)
Dennoch gelangt eine der beiden schneller ins Ziel, hat also eine höhere Durchschnittsgeschwindigkeit.
.
|
|
|
Woelfi
Gast
|
| Woelfi Verfasst am: 01. Okt 2020 17:45 Titel: |
|
|
Danke für die schnelle Antwort.
Also ich würde sagen Rolle 1 weil sie den größeren Winkel hat und dementsprechend den steileren Weg. Sie hat eine höhere Anfanggeschwindigkeit
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
| Mathefix Verfasst am: 02. Okt 2020 11:02 Titel: |
|
|
| Woelfi hat Folgendes geschrieben: | Danke für die schnelle Antwort.
Also ich würde sagen Rolle 1 weil sie den größeren Winkel hat und dementsprechend den steileren Weg. Sie hat eine höhere Anfanggeschwindigkeit |
Die Anfangsgeschwindigkeit ist in beiden Fällen gleich.
Die Steigung am Beginn der Parabel hängt davon ab, ob sie konkav oder konvex ausgerichtet ist. Mach mal eine Skizze der beiden Möglichkeiten.
|
|
|
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 829
|
| Qubit Verfasst am: 02. Okt 2020 21:57 Titel: |
|
|
| Woelfi hat Folgendes geschrieben: | | Das stimmt die Endgeschwindigkeit ist gleich aber sie soll später als bei der Parabel eintreffen und das genau ist mein Problem, warum ist das so? Weil der Winkel anders ? Also damit meine ich die Parabel ist steiler als die lineare |
Wenn du die vorgegebenen Kurven im konstanten Kraftfeld betrachtest, dann bekommst du effektiv ein vom Ort abhängiges Beschleunigungsfeld.
Da sich dann die Beschleunigungen allgemein von Ort zu Ort ändern, musst du den gesamten Kurvenverlauf (Integral) betrachten, um die benötigen Zeiten zu ermitteln. Auf der parabolischen Bahn kann der Körper dadurch auf der ersten Hälfte des Weges soviel an Geschwindigkeit gewinnen, dass dies die verringerte Beschleunigung auf der zweiten Hälfte sozusagen "überkompensiert", so dass der Körper gegenüber der Geraden Zeit "gewinnt".
Allerdings muss es nicht so sein.
Um das formelmäßig nachzuvollziehen, kannst du dir vereinfacht Perlen auf Drähten vorstellen, auf denen sie im Schwerefeld rutschen. Man habe also einfach parametrisierbare Kurven in der Ebene (ohne unendliche Steigungen, ohne sowas wie Loopings, etc.):
)
Nehmen wir jetzt zB. die Gerade und Parabel durch (0|100) und (10|0):
 = -10 \cdot x + 100 {, \;} y_2(x) = (x-10)^2)
Die Beschleunigung der Perle ist nun in jedem Punkt des Drahts die Tangentialkomponente von -g zur Kurve (die Normalkomponente wird durch eine Zwangskraft kompensiert). Die Tangente bekommt man über die Steigung m(x) als Ableitung von y(x), als Sinus vom zugehörigen Winkel der Steigung:
 = -g \cdot sin(arctan(m(x)) = -g \cdot \frac{m(x)}{\sqrt{1+m^2(x)}})
Jetzt kann man die tangentiale Geschwindigkeitkomponente berechnen:
 = \frac{d v_t(x)}{dt} = \frac{d v_t(x)}{dx} v_x(x))
Hierbei ist v_x die Cos-Komponente von v_t:
 = v_t(x) \cdot cos(arctan(m(x)) = v_t(x) \frac{1}{\sqrt{1+m^2(x)}})
Dies eingesetzt erhält man dann :
 = -g \cdot \int_0^{x_0} a_t(x) \cdot \sqrt{1+m^2(x)} \; dx = -g \int_{y(0)}^{y(x)} dy = -g \cdot (y(x)-y(0)))
N.B. Dies ist auch schon aus dem Energiesatz bekannt: )
Um jetzt die Zeiten auf den Kurven bis zum Ziel zu bekommen, kann man die Tangentialgeschwindigkeit auf die x- oder y-Komponente/Achse projizieren. Diese beiden (1-D) Bewegungen laufen unterschiedlich ab, aber benötigen gleiche Zeiten bis zu einem Punkt auf der Kurve.
zB. für die x-Komponente:
 = v_t(x) \cdot cos(arctan(m(x)) = v_t(x) \cdot \frac{1}{\sqrt{1+m^2(x)}} = \frac{\sqrt{ -2g \cdot (y(x)-y(0))}}{\sqrt{1+m^2(x)}} = \frac{d x}{d t})
Integriert man das, dann bekomt man schließlich (mit m(x) = y'(x)) für die benötigte Zeit:
}}{\sqrt{ -2g \cdot (y(x)-y(0))}} \; dx })
Auf die Fälle angewendet:
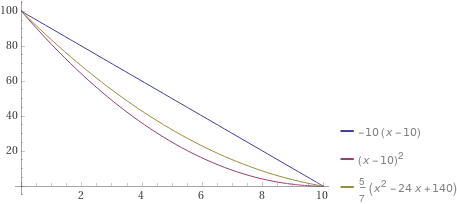
(1) y(x) = -10x+100, m(x)=-10
^2}}{\sqrt{-2 \cdot 9.81 \cdot (-10 x)}} \; dx \approx 4.538s)
(2) y(x) = (x-10)^2, m(x) = 2x-20
^2}}{\sqrt{-2 \cdot 9.81 \cdot ((x - 10)^2 - 100)}} \; dx \approx 4.543s)
In diesem Fall erreicht man also auf der Geraden schneller das Ziel.
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
| Mathefix Verfasst am: 03. Okt 2020 11:36 Titel: |
|
|
| Qubit hat Folgendes geschrieben: |
(2) y(x) = (x-10)^2, m(x) = 2x-20
|
@Qubit
Hallo Qubit,
super!
Würdest Du bitte die Zeit T_3 für den Fall der konkaven Parabel, die durch die gleichen Punkte (0/100); (10/0) geht berechnen
 y(x) = 100 - x^{2} )
Mein Integralrechner streikt dabei.
Beste Grüsse
mathefix
|
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
| Myon Verfasst am: 03. Okt 2020 13:03 Titel: |
|
|
Zeit für die nach unten geöffnete Parabel (y=100-x^2)): T3=6.217s.
Für die schnellste Bahn siehe Brachistochrone.
|
|
|
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 829
|
| Qubit Verfasst am: 03. Okt 2020 13:53 Titel: |
|
|
| Mathefix hat Folgendes geschrieben: |
Mein Integralrechner streikt dabei.
|
Das ist ein "pathologischer Fall", da y'(0) = 0 (labiles Gleichgewicht). Je näher am Nullpunkt, desto länger dauert das "Fallen".
|
|
|
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 829
|
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 03. Okt 2020 15:43 Titel: |
|
|
| Zitat: | | Für die schnellste Bahn siehe Brachistochrone. |
Das interessante daran ist, dass der tiefste Punkt unterhalb des Zielpunktes liegt, und das die Strecke länger ist, als der direkte Weg.
Dennoch kommt die Rolle auf dieser Bahn am schnellsten an, auch wenn die Endgeschwindigkeiten gleich sind.
Man hat also am Ende die gleiche kinetische Energie, ist aber auf der Brachistochrone schneller.
In der Natur hat sich das auch schon herumgesprochen. Wenn man Vögel beobachtet, wie sie von einem hohen Ast startend zu einem niedrigerem Ast gleiten, dann ähnelt die Flugbahn erstaunlich oft dieser Kurve.
.
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
| Mathefix Verfasst am: 03. Okt 2020 16:50 Titel: |
|
|
[quote="Myon"]Zeit für die nach unten geöffnete Parabel (y=100-x^2)): T3=6.217s.
@Myon
| Qubit hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: |
Mein Integralrechner streikt dabei.
|
Das ist ein "pathologischer Fall", da y'(0) = 0 (labiles Gleichgewicht). Je näher am Nullpunkt, desto länger dauert das "Fallen". |
Hallo Myon, wie kommst Du auf Dein Ergebnis?
|
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
| Mathefix Verfasst am: 03. Okt 2020 19:57 Titel: |
|
|
| Qubit hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: |
Mein Integralrechner streikt dabei.
|
Das ist ein "pathologischer Fall", da y'(0) = 0 (labiles Gleichgewicht). Je näher am Nullpunkt, desto länger dauert das "Fallen". |
Verstehe ich nicht. Im Fall der Geraden und der konvexen Parabel herrscht ebenfalls labiles Gleichgewicht, da der Schwerpunkt des Zylinders senkrecht über dem Startpunkt liegt
In allen Fällen ist ein Impuls notwendig, damit der Zylinder ins Rollen kommt.
|
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
| Myon Verfasst am: 03. Okt 2020 20:21 Titel: |
|
|
| Mathefix hat Folgendes geschrieben: | | Hallo Myon, wie kommst Du auf Dein Ergebnis? |
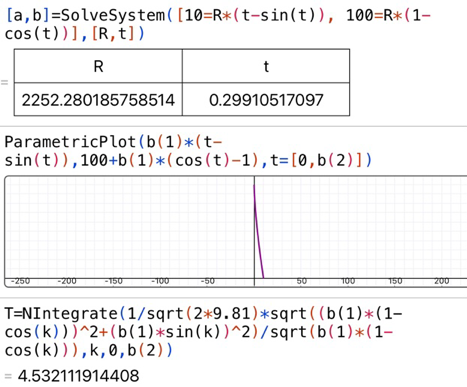
Indem ich, ohne irgendetwas weiter zu überlegen, das Integral mit einem Programm nummerisch gelöst habe.  Das war aber nicht so schlau, denn wie Qubit schreibt, je näher beim Nullpunkt man startet bzw. je kleiner die Startgeschwindigkeit ist, um aus dem labilen Gleichgewicht zu kommen, umso grösser ist die Zeit - diese ist nicht nach oben beschränkt.
Das Integral für die Zeit verhält sich bei 0 wie das Integral von 1/x, was ebenfalls divergiert.
Die Zeit für die Brachistochrone beträgt t=4.532s. Aufgrund der (betragsmässig) grossen Steigung ist der Zeitgewinn verglichen mit den obigen Parabeln gering.
| Frankx hat Folgendes geschrieben: | | Zitat: | | Für die schnellste Bahn siehe Brachistochrone. |
Das interessante daran ist, dass der tiefste Punkt unterhalb des Zielpunktes liegt, und das die Strecke länger ist, als der direkte Weg. |
Dass der tiefste Punkt unterhalb des Zielpunktes ist, gilt nur für den Fall, wo die Steigung zwischen Anfangs- und Endpunkt betragsmässig kleiner als 2/pi ist. Vgl. den Wikipedia-Artikel.
| Beschreibung: |
|
| Dateigröße: |
129.94 KB |
| Angeschaut: |
885 mal |
|
|
|
|
|
Registrieren
Login
FAQ
Suchen
