| Autor |
Nachricht |
bellaszy
Anmeldungsdatum: 30.11.2008
Beiträge: 14
|
 bellaszy Verfasst am: 30. Nov 2008 18:40 Titel: Hohlzylinder & Vollzylinder Rampe hinauf, h nur mit v? : bellaszy Verfasst am: 30. Nov 2008 18:40 Titel: Hohlzylinder & Vollzylinder Rampe hinauf, h nur mit v? : |
 |
|
Hallo Leute,
ich muss leider ein paar Übungsaufgaben erledigen und ich bin hier bei einer Aufgabe, bei der ich echt nicht weiterkomme:
Ein dünnwandiger Hohlzylinder und ein Vollzylinder rollen horizontal mit einer Geschwindigkeit v= 1m/s und treffen auf eine schiefe Ebene, die sie ohne zu gleiten hinauf rollen. In welcher Höhe hd und hv kommen die beiden Zylinder jeweils zum stehen?
...
also ich hab ja damit jetzt schon einige Zeit verbacht... ich weiß, dass ich das aus E berechnen muss, und mit J. ...
ich hab nur echt keinen Plan, wie ich das ohne noch irgendwas wie m oder radius ausrechnen soll...! Sad(
ich komm einfach nicht voran Sad
vielleicht hat ja einer eine "Tricky"-Idee
Viele liebe Grüße |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. Nov 2008 18:46 Titel: dermarkus Verfasst am: 30. Nov 2008 18:46 Titel: |
 |
|
Tipp:
* Rechne mal nur mit Formeln, und nicht mit konkreten Zahlenwerten. Kürzt sich dann so etwas wie das 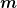 und das und das  am Ende raus? am Ende raus?
* Hast du schon einen festen Zusammenhang dafür gefunden, wie die Winkelgeschwindigkeit  und die Translationsgeschwindigkeit und die Translationsgeschwindigkeit  miteinander zusammenhängen müssen, wenn die Zylinder rollen? miteinander zusammenhängen müssen, wenn die Zylinder rollen?
Magst du mal zeigen, wie weit du damit schon kommst? |
|
 |
bellaszy
Anmeldungsdatum: 30.11.2008
Beiträge: 14
|
 bellaszy Verfasst am: 30. Nov 2008 22:12 Titel: bellaszy Verfasst am: 30. Nov 2008 22:12 Titel: |
 |
|
....
ich verstehe das nicht wirklich.
eigentlich kann ich auch nicht richtig mit formeln so rechnen,
weil ich die logik dran gerade überhaupt nicht verstehe...
wenn ich jetzt zb.
oderoderoder dann
....was mache ich dann damit??
ich kann doch da nicht lustig rumstreichen und was wegkürzen   |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. Nov 2008 22:50 Titel: dermarkus Verfasst am: 30. Nov 2008 22:50 Titel: |
 |
|
Okay, viele der Formeln, die du dann in dieser Aufgabe an der einen oder anderen Stelle auf deinem Rechenweg brauchen wirst, hast du also offenbar schon.
Was möchtest du nun damit rechnen? Was für einen Rechenweg würdest du dafür vorschlagen, und wie würdest du damit anfangen? Wie würdest du anfangen, zu beschreiben, wie so ein Zylinder den Hang hochrollt? |
|
 |
bellaszy
Anmeldungsdatum: 30.11.2008
Beiträge: 14
|
 bellaszy Verfasst am: 30. Nov 2008 23:03 Titel: bellaszy Verfasst am: 30. Nov 2008 23:03 Titel: |
 |
|
hmmm also erstmal..
bin ich sooo froh das du noch online bist !! 
*hug*
also ich würde sagen, das man aus der erst Ekin + Erot auf der Schräge =Epot errechnet..
dann wüsste ich eigentlich nur noch w=v/r,
ich kann mir irgendwie schwer vorstellen, ob die aufgabe nun theoretisch beantwortet werden soll oder doch mathematisch?
sonst fällt mir dann dazu nur noch ein, dass der Hohlzylinder weiter kommen müsste als der Vollzylinder
(Obwohl bei "bergab" der Vollzylinder wegen der "vollmasse" halt weniger umdrehungen hat und deshalb schneller ist, aber ich denke mal auf eine schräge hinauf wird er ja träger sein?) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. Nov 2008 23:16 Titel: dermarkus Verfasst am: 30. Nov 2008 23:16 Titel: |
 |
|
| bellaszy hat Folgendes geschrieben: |
also ich würde sagen, das man aus der erst Ekin + Erot auf der Schräge =Epot errechnet..
dann wüsste ich eigentlich nur noch w=v/r,
|
Prima, einverstanden 
Nur Mut, magst du damit mal anfangen, konkret loszurechnen? Wie weit kommst du damit? |
|
 |
bellaszy
Anmeldungsdatum: 30.11.2008
Beiträge: 14
|
 bellaszy Verfasst am: 30. Nov 2008 23:22 Titel: bellaszy Verfasst am: 30. Nov 2008 23:22 Titel: |
 |
|
also
m/2xv² + 1/2x Jxw²=mxgxh
und dann
m/2xv²+J/2xw²=mxgxh
... mehr fällt mir nicht ein  |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. Nov 2008 23:25 Titel: dermarkus Verfasst am: 30. Nov 2008 23:25 Titel: |
 |
|
Einverstanden 
Was wolltest du nun aus diesen Formeln ausrechnen? Was ist gesucht, was ist bekannt?
(Tipp am Rande: Schreibe deine Malzeichen gerne als * und nicht als x, sonst liest man immer "ix" und findet die Gleichungen ziemlich schwer zu lesen  Oder verwende natürlich am besten wieder Latex, damit lesen sich die Formeln sowieso am besten.) Oder verwende natürlich am besten wieder Latex, damit lesen sich die Formeln sowieso am besten.) |
|
 |
bellaszy
Anmeldungsdatum: 30.11.2008
Beiträge: 14
|
 bellaszy Verfasst am: 30. Nov 2008 23:26 Titel: bellaszy Verfasst am: 30. Nov 2008 23:26 Titel: |
 |
|
hmm vielleicht noch
m/2 x v²+MxR²/2 x v/R0mxgxh |
|
 |
bellaszy
Anmeldungsdatum: 30.11.2008
Beiträge: 14
|
 bellaszy Verfasst am: 30. Nov 2008 23:29 Titel: bellaszy Verfasst am: 30. Nov 2008 23:29 Titel: |
 |
|
naja nur v ist bekannt. und wahrscheinlich g.
m/2 * (1m/s²)²+M*R²/2 * 1m/s²/2 = m*9,81m/s²*h |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. Nov 2008 23:29 Titel: dermarkus Verfasst am: 30. Nov 2008 23:29 Titel: |
 |
|
Ja, ein bisschen so umformen durch einsetzen, so dass die Größen in der Gleichung stehen, die du kennst, ist eine der guten Ideen in dieser Gleichung. (Was meinst du mit dem M ?)
Aber schau dir zuerst mal an, welches Ziel du mit dieser Gleichung erreichen möchtest: Was möchtest du mit dieser Gleichung ausrechnen? |
|
 |
bellaszy
Anmeldungsdatum: 30.11.2008
Beiträge: 14
|
 bellaszy Verfasst am: 30. Nov 2008 23:31 Titel: bellaszy Verfasst am: 30. Nov 2008 23:31 Titel: |
 |
|
|
kann ich das auf R=m*g*h runterkürzen oder ist das zu hart? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. Nov 2008 23:34 Titel: dermarkus Verfasst am: 30. Nov 2008 23:34 Titel: |
 |
|
| bellaszy hat Folgendes geschrieben: | naja nur v ist bekannt. und wahrscheinlich g.
m/2 * (1m/s²)²+M*R²/2 * 1m/s²/2 = m*9,81m/s²*h |
Zahlenwerte solltest du erst mal noch nicht einsetzen, denn dann bleibt die Gleichung übersichtlicher.
Erst einmal geht es um die Frage: Was willst du mit dieser Gleichung ausrechnen? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. Nov 2008 23:39 Titel: dermarkus Verfasst am: 30. Nov 2008 23:39 Titel: |
 |
|
| bellaszy hat Folgendes geschrieben: | hmm vielleicht noch
m/2 x v²+MxR²/2 x v/R0mxgxh |
Vergiss nicht, all die Rechenzeichen zu setzen, die nötig sind. Sonst bekommst du unnötige Rechenfehler einfach nur durch falsches Abschreiben deiner Gleichungen beim Einsetzen. |
|
 |
bellaszy
Anmeldungsdatum: 30.11.2008
Beiträge: 14
|
 bellaszy Verfasst am: 30. Nov 2008 23:40 Titel: bellaszy Verfasst am: 30. Nov 2008 23:40 Titel: |
 |
|
|
hmm also ich brauch ja die beiden E um herauszufinden, wer von den beiden (denke ich mal dass das so gemeint ist) am meisten in E umsetzt um dann "am höchsten" zu kommen. die eigentliche frage ist ja die nach den jeweilgen h('s) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 30. Nov 2008 23:41 Titel: dermarkus Verfasst am: 30. Nov 2008 23:41 Titel: |
 |
|
Einverstanden, du willst die h's wissen.
Magst du mal mit der Gleichung für den Hohlzylinder anfangen? Wie lautet dessen Trägheitsmoment und wie lautet folglich die Gleichung für die Höhe 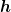 , die der Hohlzylinder am Hang erreicht? , die der Hohlzylinder am Hang erreicht? |
|
 |
bellaszy
Anmeldungsdatum: 30.11.2008
Beiträge: 14
|
 bellaszy Verfasst am: 01. Dez 2008 12:55 Titel: bellaszy Verfasst am: 01. Dez 2008 12:55 Titel: |
 |
|
Hi,
sorry das ich gestern nicht mehr geschrieben habe, aber ich war wohl schon so verpeilt, dass ich nicht gemerkt habe, dass es auf der 2ten seite weitergeht!
hmm also für den Hohlzylinder wäre das

aber wie bekomme ich dadurch die Höhe raus?
Eigentlich habe ich als Unbekannte ja noch die Masse? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 01. Dez 2008 13:09 Titel: dermarkus Verfasst am: 01. Dez 2008 13:09 Titel: |
 |
|
| bellaszy hat Folgendes geschrieben: |
hmm also für den Hohlzylinder wäre das

|
Einverstanden  Setz das mal ein. Setz das mal ein.
Wie lautet damit deine Gleichung? |
|
 |
bellaszy
Anmeldungsdatum: 30.11.2008
Beiträge: 14
|
 bellaszy Verfasst am: 01. Dez 2008 13:31 Titel: bellaszy Verfasst am: 01. Dez 2008 13:31 Titel: |
 |
|
hmm
 |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 01. Dez 2008 13:37 Titel: dermarkus Verfasst am: 01. Dez 2008 13:37 Titel: |
 |
|
Einverstanden, das Trägheitsmoment hast du richtig in diese Gleichung eingesetzt 
Pass nun aber noch beim Einsetzen der Winkelgeschwindigkeit auf: Hast du dabei nicht noch etwas vergessen? |
|
 |
bellaszy
Anmeldungsdatum: 30.11.2008
Beiträge: 14
|
 bellaszy Verfasst am: 01. Dez 2008 13:42 Titel: bellaszy Verfasst am: 01. Dez 2008 13:42 Titel: |
 |
|
|
ah ja okay noch ² |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 01. Dez 2008 13:45 Titel: dermarkus Verfasst am: 01. Dez 2008 13:45 Titel: |
 |
|
Okay, wie lautet damit deine Gleichung, wenn du sie sauber und komplett aufschreibst?
Tipp: Verwende dazu gerne in Latex den Befehl \frac{}{} für Brüche (zum Beispiel 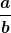 ) und \cdot für die Malpunkte (zum Beispiel ) und \cdot für die Malpunkte (zum Beispiel 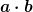 ), dann wirds besonders übersichtlich. ), dann wirds besonders übersichtlich. |
|
 |
bellaszy
Anmeldungsdatum: 30.11.2008
Beiträge: 14
|
 bellaszy Verfasst am: 01. Dez 2008 13:47 Titel: bellaszy Verfasst am: 01. Dez 2008 13:47 Titel: |
 |
|
²=m*g*h ) |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 01. Dez 2008 13:49 Titel: dermarkus Verfasst am: 01. Dez 2008 13:49 Titel: |
 |
|
Einverstanden, nun stimmt diese Gleichung.
Aber ist sie auch schon übersichtlich genug aufgeschrieben, dass du es nun schaffen kannst, diese Gleichung durch Rechnen und Umformen Schritt für Schritt zu vereinfachen und am Ende nach h umzustellen? |
|
 |
|



















 Oder verwende natürlich am besten wieder Latex, damit lesen sich die Formeln sowieso am besten.)
Oder verwende natürlich am besten wieder Latex, damit lesen sich die Formeln sowieso am besten.)