| Autor |
Nachricht |
Phase1997
Anmeldungsdatum: 22.07.2018
Beiträge: 14
|
 Phase1997 Verfasst am: 14. Jul 2020 09:31 Titel: Zwei ununterscheidbare Bosonen in attraktivem Potenzial |
 |
|
Hey zusammen 
Ich bin mir bei einer Aufgabe zur Prüfungsvorbereitung unsicher, ob meine Lösungsweg soweit richtig ist und wie ich zum Schluss die Aufgabe zu verstehen habe.
Die Aufgabe lautet folgendermaßen:
Bestimmen Sie die Grundzustandsenergie zweier Bosonen der Masse m in einer Dimension unter dem attraktiven Potenzial
 = K/2 (x_1-x_2)^2 )
und vergleichen sie diese ohne Rechnung mit der Grundzustandsenergie von Spin-1/2 Fermionen im Spin-Singulett bzw- Spin-Triplett Zustand.
Der Hamiltonoperator des Systems lautet dann
 + K/2 (x_1-x_2)^2 ) .
Mit den Relativkoordinaten im Schwerpunktsystem
 )
komme ich auf den neuen Hamiltonoperator
Damit sieht es ja so als, als wäre es ein System mit einem freien Teilchen der Masse 2m und einem Teilchen im Potential mit  und der Masse m/2. Ich denke soweit sogut.
Nun ist die Frage, wie sich daraus die Grundzustandsenergie ergibt. Für unterscheidbare Teilchen
 = \Psi_1(x_1)\Psi_2(x_2) )
würde sich ja eine Grundzustandsenergie ergeben von
 + (n+1/2) \hbar \omega_x(K,m) ) ?
Wie ist das nun für ununterscheidbare Bosonen zu handhaben, da sie ja die komplett symmetrische Wellenfunktion
 = \dfrac{\Psi_1(x_1)\Psi_2(x_2) + \Psi_1(x_2)\Psi_2(x_1)}{\sqrt{2}})
haben?
Mein Vorschlag wäre
 + (n+1/2) \hbar \omega_x(K,m) + \hbar \omega_x(m) + (n+1/2) \hbar \omega_R(K,m)). )
Sozusagen die Superposition aus den Zuständen, wenn der Schwrpunkt frei ist und das Teilchen mit m/2 im harmonischen Oszillator ist und umgekehrt. Das sieht aber intuitiv komisch aus...
Im Vergleich zu Fermionen hätte ich gesagt, dass Bosonen eher näher beeinander liegen und Fermionen eher weiter weg, was sich ja aus den (anti-)symmetrischen Wellenfunktion ergibt. Daher müsste meines erachtens die Grundzustandsenergie von Fermionen größer sein, als die von Bosonen, da 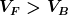 sein müsste, oder? Mit meiner Lösung ist das aber nicht kompatibel, da sich ja bei Fermionen ein Minus einschleicht.
Ich hoffe mir kann jemand helfen. Ich freue mich sehr auf eine Diskussion! |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 14. Jul 2020 12:37 Titel: |
|
|
Dein Ansatz für die Schwerpunktskoordinate R passt nicht.
Es gilt ja
 = H_R + H_x )
mit Gesamtmasse M und Gesamtimpuls P.
Man findet
(eigentlich müsstest du das Verschwinden der relevanten Kommutatoren explizit zeigen)
Daher separiert die Schrödingergleichung, und man verwendet den Ansatz
 = \Phi(R) \, \phi(x))
Für die Wellenfunktion zur Schwerpunktskoordinate R erhält man eine ebene Welle mit den erhaltenen Gesamtimpuls K.
 \sim e^{iKR})
Für die Relativkoordinate x folgen dann die Einteilchen-Wellenfunktionen des harmonischen Oszillators
)
 \, \phi_n)
Für die Gesamtwellenfunktion gilt dann
 = \Phi_K(R) \, \phi_n(x))
Das sind deine gesuchten Zweiteilchen-Wellenfunktionen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 15. Jul 2020 07:33, insgesamt 2-mal bearbeitet |
|
|
Phase1997
Anmeldungsdatum: 22.07.2018
Beiträge: 14
|
| Phase1997 Verfasst am: 14. Jul 2020 13:38 Titel: |
|
|
Danke für die Antwort!
Also der Ansatz für die Schwerpunktskoordinate sollte doch
 )
sein, oder?
Und damit komme ich ja letztendlich genau auf deinen Hamiltonoperator.
Mir ist die Argumentation soweit klar ich frage mich jetzt nur, welchen unterschied es gibt, wenn ich ununterscheidbare Bosonen oder Fermionen betrachte. Vorallem dann in Hinblick auf die Grundzustandsenergie.
Ich müsste doch dann eigentlich noch den Ansatz
=\frac{\Psi_{1}\left(x_{1}\right) \Psi_{2}\left(x_{2}\right)+\Psi_{1}\left(x_{2}\right)\Psi_{2}\left(x_{1}\right)}{\sqrt{2}} )
verwenden mit
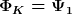
und dann müsste ich in der Konsequenz auch auf meine Energie
 \hbar \omega_{x, harm}+\dfrac{\hbar^2 k^2}{2\mu}+(n+\dfrac{1}{2}) \hbar \omega_{R, harm} \right))
kommen mit  der Kreisfrequenz des harmonischen Potenzials  und K, k die Wellenzahlen des Schwerpunktes R und dem relativen Teiclhen x, oder habe ich die Lösung falsch verstanden? |
|
|
Phase1997
Anmeldungsdatum: 22.07.2018
Beiträge: 14
|
| Phase1997 Verfasst am: 14. Jul 2020 17:31 Titel: |
|
|
Also meine Grundzustandsenergie folgt aus dem Ansatz der Wellenfunktion für Bosonen. Es ist sozusagen die Superpositionierte Energie. Aber das muss ja auch nicht richtig sein, bzw. wird es ja wahrscheinlich auch nicht, weil wie du sagstest, mit den neuen Koordinaten sind die Teilchen bei R und x ja nicht mehr identisch.
Aus meiner Sicht scheint es so, als wäre es egal, ob die Ausgangsteilchen unterscheidbar sind, oder nicht und ob Fermion oder Boson, da im neuen System sie ja ohnehin unterscheidbar werden. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 14. Jul 2020 20:07 Titel: |
|
|
Ich hatte ein Brett vor dem Kopf.
Wir dachten wohl beide an einen Ansatz der Form
 \sim \phi_A(x_1) \, \phi_B(x_2) \pm \phi_B(x_1) \, \phi_A(x_2))
Dieser Ansatz liefert unter Verwendung der Einteilchen-Wellenfunktionen für den Austauschoperator
 = \psi_{AB}(x_2, x_1) = \pm \psi_{AB}(x_1, x_2))
Der Ansatz ist dann sinnvoll, wenn die Einteilchen-Wellenfunktionen bekannt und nützlich sind, insbs. bei (näherungsweise) freien Teilchen.
Das ist hier jedoch nicht der Fall!
Wir kennen die Einteilchen-Wellenfunktionen nicht, dafür jedoch die exakten Lösungen für die Zweiteilchen-Wellenfunktionen, nämlich
 = e^{iKR} \, h_n(x))
mit ebenen Wellen in R sowie den Hermite-Funktionen in x.
Die ebene Welle in R beschreibt eine gleichförmige Translation des Schwerpunktes des Zweiteilchensystems mit Impuls K, die Hermite-Funktionen die Oszillation in der Relativkoordinate x.
Diese Zweiteilchen-Wellenfunktionen sind bereits Eigenfunktionen zum Austauschoperator, denn aus
sowie den Eigenfunktionen des harmonischen Oszillators mit
 = (-)^n \, h_n(x))
folgt für den Austauschoperator
 = e^{iKR} \, h_n(-x) = e^{iKR} \, (-)^n \, h_n(x) = (-)^n \, \Psi_{K,n}(R,x))
D.h. Symmetrisierung (bzw. Antisymmetrisierung) ist nicht mehr notwendig.
Für Bosonen müssen die Wellenfunktionen symmetrisch bzgl. Vertauschung der Teilchen sein, d.h. es ist nur das Vorzeichen + und damit nur geradzahliges n zulässig.
D.h. wir haben für die Oszillation in der Relativkoordinate x die zulässigen Wellenfunktionen zu n = 0,2,4,... mit den Energieeigenwerten
)
sowie dem Grundzustand
 = e^{iKR} \, h_0(x))
Für Bosonen bist du demnach bereits fertig.
Für Fermionen musst du die Rechnung noch um den Spin-Anteil der Wellenfunktion erweitern, dessen Symmetrie unter Vertauschung berücksichtigen und Antisymmetrie für die Gesamtwellenfunktion (in R,x, s_1, s_2) herstellen. Dabei kannst du natürlich ausnützen, dass die Lösungen bzgl. der Spinorientierungen entartet sind, weil der Hamiltonoperator spin-unabhängig ist.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Phase1997
Anmeldungsdatum: 22.07.2018
Beiträge: 14
|
| Phase1997 Verfasst am: 16. Jul 2020 14:30 Titel: |
|
|
Danke! Das macht jetzt auf jeden Fall einiges klarer!
Die einzige Frage die noch bleibt, wäre, wo man für Fermionen jetzt wirklich den Spinanteil noch mit betrachten muss? Weil egal ob ich ein symmterischen oder antisymmetrischen Ortsanteil habe, kann ja der Spinanteil wiederum symmterisch oder antisymmetrisch sein. Damit wäre für Fermionen n=1,2,3... möglich.
Ein zweiter Gedanke wäre, dass man den Spinanteil weiterhin nicht betrachtet und dann nur gerade n mit deiner Argumentation möglich wäre. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 16. Jul 2020 15:42 Titel: |
|
|
Schauen wir uns zunächst wieder die aus den Produktzuständen konstruierten antisymmetrisierten Zustände an:
 \sim \phi_A(1)\chi_A(1) \, \phi_B(2)\chi_B(2) - (1 \longleftrightarrow 2))
mit den Zweier-Spinoren chi.
Die Antisymmetrisierung gilt für den gesamten Zustand; d.h.
 \sim \phi_A(2)\chi_A(2) \, \phi_B(1)\chi_B(1) - (1 \longleftrightarrow 2) = - \psi_{AB}(2,1) )
Nun verwenden wir jedoch nicht diese Konstruktion, sondern die o.g. bosonischen Zweiteilchenzustände
 \, \phi_n(x) )
Außerdem ist der Hamiltonian spinunabhängig
 = H(R,x) \cdot 1_1 \cdot 1_2)
d.h. wir haben den Ortsanteil wie oben sowie den Spinanteil, der für 1,2 jedoch jeweils der 2x2 Einheitsmatrix 1_1, 1_2 entspricht (also keine Paulimatrix enthält).
D.h. wir können einen Produktansatz wählen:
 = \Phi_K(R) \, \phi_n(x) \, \chi(1,2))
Für die Wirkung des Austauschoperators gilt
 = P_{1,2} \, [\Phi_K(R) \, \phi_n(x) \, \chi(1,2)] = (-)^n \, \Phi_K(R) \, \phi_n(x) \, P_{1,2} \, \chi(1,2) \stackrel{!}{=} - \Psi(1,2))
mit
 = \chi(2,1))
Ersteres wissen wir von oben. Letzteres ist die Forderung nach Antisymmetrie des Gesamtzustandes. D.h. wir benötigen eine Fallunterscheidung für gerades bzw. ungerades n:
: \; \chi(2,1) = - \chi(1,2))
: \; \chi(2,1) = + \chi(1,2))
Für gerades n ist der Ortsanteil symmetrisch bzgl. des Austauschoperators - das haben wir oben abgeleitet - d.h. der Spinanteil muss antisymmetrisch sein, damit der Gesamtzustand ebenfalls antisymmetrisch ist.
Für ungerades n ist der Ortsanteil antisymmetrisch bzgl. des Austauschoperators - das haben wir oben abgeleitet - d.h. der Spinanteil muss jetzt symmetrisch sein, damit der Gesamtzustand wiederum antisymmetrisch ist.
Die symmetrischen bzw. antisymmetrischen 2x2-Spinoren konstruierst du nun gemäß
 = \chi(1) \, \chi(2) \pm \chi(2) \, \chi(1))
wobei du zwei Fälle hast, nämlich einmal Singulett = Gesamtspin 0, einmal Triplett = Gesamtspin 1.
Dann einsetzen und die bzgl. Symmetrie / Antisymmetrie erlaubten 2x2-Spinoren identifizieren.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
