| Autor |
Nachricht |
ThisGuy
Gast
|
 ThisGuy Verfasst am: 11. Jun 2020 00:08 Titel: Elastizitätsmodul eines Aluminium-Vollbalken berechnen |
 |
|
Meine Frage:
Ein Aluminium-Vollbalken 1 mit quadratischem Querschnitt(b = 8 mm) und ein Aluminium-Balken 2 mit Doppel-T-förmigem Querschnitt (B = 12 mm, d = 2 mm) werden jeweils durch eine im Abstand x = l = 51,5 cm von der Einspannstelle (x = 0) in negativer z-Richtung angreifenden Kraft F um die Strecke s (Projektion auf die Vertikale) mit s~F nach unten verbogen.
a) Leiten Sie Formeln für die Flächenträgheitsmomente ) bzw. ) der beiden Balken her und berechnen Sie deren Werte!
Hinweis:  , wobei die -z-Richtung die Richtung der wirkenden Kraft ist.
b) Beim Aluminium-Vollbalken 1 ist s(20N) = 4,0 cm. Bestimmen Sie daraus den Elastizitätsmodul E und geben Sie die Funktionsgleichung z(x) der Biegelinie für F = 20 N an!
Ich habe bereits das Flächenträgheitsmoment für den Vollbalken bestimmt und auch ein Ergebnis für den T-Balken. Allerdings habe ich mein Ergebnis mit dem was in der Tabelle im unteren Teil des Wikipedia-Artikels zu Flächenträgheitsmoment(https://de.wikipedia.org/wiki/Flächenträgheitsmoment) steht, verglichen und es stimmt nicht überein. Könnte mir jemand erklären wie man es richtig bestimmt?
Weiterhin habe ich bei der b) zwar einen Ansatz, dieser erscheint mir aber nicht korrekt zu sein. Ich werde auf diesen in den Ideen schildern.
Wenn mir jemand bei diesen Dingen helfen könnte, wäre ich sehr dankbar! :)
Meine Ideen:
Zu a):
Das Flächenträgheitsmoment des Doppel-T-Balkens habe ich berechnet, indem ich das gegebene Integral aus dem Hinweis verwende, den Balken in 3 Teile zerlege und die Trägheitsmomente der einzelnen Teile berechne und dann addiere. Mein Ergebnis ist dann  . Diese Gleichung unterscheidet sich von der aus dem Wikipedia-Artikel, darum bin ich mir sicher, dass sie nicht stimmt.
Zu b):
Bei der b) dachte ich mir, dass man die folgende Formel zur Berechnung der Kraft verwenden kann,  und diese mit Hilfe des Pythagoras nach 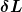 umstellt. Die Motivation dahinter ist, dass die Dehnung des Balkens ja in die Vertikale geht, man diese Formel aber, glaube ich, normalerweise nur für die Horizontale verwendet. Da die Biegung allerdings nicht unbedingt wie eine gerade, sondern auch eine Kurven sein kann, bin ich nicht gerade von diese Ansatz überzeugt. |
|
 |
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 11. Jun 2020 09:20 Titel: |
|
|
| Zitat: | Mein Ergebnis ist dann . .....
Diese Gleichung unterscheidet sich von der aus dem Wikipedia-Artikel, darum bin ich mir sicher, dass sie nicht stimmt. |
Schau dir die Potenzen in der Summe über dem Bruchstrich an. Das kann schon von den Einheiten her nicht stimmen.
Beachte bei der Addition der einzelnen Flächenträgheitsanteile auch die Steineranteile!
| Zitat: | | Die Motivation dahinter ist, dass die Dehnung des Balkens ja in die Vertikale geht, man diese Formel aber, glaube ich, normalerweise nur für die Horizontale verwendet. Da die Biegung allerdings nicht unbedingt wie eine gerade, sondern auch eine Kurven sein kann, bin ich nicht gerade von diese Ansatz überzeugt. |
Man geht bei diesen Berechnungen von verhältnismäßig (zur Bauteillänge) relativ kleinen vertikalen Verschiebungen (Durchbiegungen) aus. Deshalb darf man die "Längung" des Balkens vernachlässigen.
Bei größeren Verformungen bewegt man sich meist sowieso nicht mehr im linearelastischem Bereich und da gibt es andere Berechnungsmöglichkeiten.
. |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
| Mathefix Verfasst am: 11. Jun 2020 09:52 Titel: |
|
|
1. Hast Du bei der Berechnung des Flächenträgheitsmoments des Doppel-T- Trägers den Satz von Steiner berücksichtigt?
2. Den Elastizitätsmodul kannst Du aus der Biegegleichung eines Balkens
 = \frac{M(x)}{E\cdot I} )
ermitteln.
Kommst Du damit weiter? |
|
|
ThisGuy
Gast
|
| ThisGuy Verfasst am: 11. Jun 2020 10:04 Titel: |
|
|
Tatsächlich habe ich nicht erwartet, dass man den Satz von Steiner dafür benötigt, aber wenn ich jetzt darüber nachdenke macht es vollkommen Sinn!
Vielen Dank, ich probiere es mal aus!  |
|
|
ThisGuy
Gast
|
| ThisGuy Verfasst am: 11. Jun 2020 18:47 Titel: Biegemoment bestimmen |
|
|
Hallöchen! Ich habe es tatsächlich geschafft das Flächenträgheitsmoment des Doppel-T-Balkens zu bestimment, aber bei der b) bin ich bisher trotzdem nicht weiter gekommen.
Ich habe versucht die Formel zur Berechnung des Biegemoments M(x), M(x) = P*(L-x), zu benutzen um dieses dann in der Formel für die Biegelinie zu verwenden, aber ich weiss leider nur die Kraft F bzw. P und die Entfernung zur Einspannstelle L. Ohne x kann ich dies meines Wissens nach nicht machen, weshalb ich das Biegemoment und somit die Biegelinie nicht bestimmen kann.
Gegeben habe ich wiederum zwar die Strecke der Verbiegung s, aber ich weiss nicht was ich damit anfangen soll bzw. wie ich diese benutze um E zu bestimmen. Weder im Internet noch in meiner Literatur habe ich dazu bisher nichts finden können.
Wäre wirklich der Hammer wenn mir jemand noch zeigen könnte wie dies funktioniert! |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
| Mathefix Verfasst am: 11. Jun 2020 19:45 Titel: |
|
|
Um M(x) berechnen zu können, ist die Länge des Balkens erforderlich.
Wenn Du die hast, kannst Du durch zweimalige Integration der Biegefunktion z(x) bestimmen.
An der Stelle x des Kraftangriffspunkts ist z = s.
Jetzt sind s, M und I vorhanden: Formel zur Biegelinie nach E umstellen.
Zuletzt bearbeitet von Mathefix am 11. Jun 2020 20:08, insgesamt einmal bearbeitet |
|
|
ThisGuy
Gast
|
| ThisGuy Verfasst am: 11. Jun 2020 19:52 Titel: |
|
|
|
Das ist ja mein Problem, ich habe die Länge nicht gegeben. Alles was gegeben ist ist in der Einleitung der Übung. Ich weiss nicht wie ich die b) lösen soll :/ |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
| Myon Verfasst am: 11. Jun 2020 19:56 Titel: |
|
|
|
Doch, Du hast doch gegeben, dass bei x=l=51.5cm die Kraft angreift. |
|
|
ThisGuy
Gast
|
| ThisGuy Verfasst am: 11. Jun 2020 20:01 Titel: |
|
|
|
Würde das dann aber nicht bedeuten, dass das Biegemoment = 0 ist, da die Gleichung M(x) = P*(l-x) ist und somit M(x) = 20*(0,518-0,518) = 0? |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
| Myon Verfasst am: 11. Jun 2020 20:05 Titel: |
|
|
Es gilt
=F_0(L-x))
wenn F0 die Kraft ist, die bei x=L angreift. Bei der Einspannstelle ist M(0)=0.
Dann wie erwähnt zweimal Integrieren und die Randbed.
=z'(0)=0)
berücksichtigen. Das führt auf den Verlauf der neutralen Faser
= \frac{F_0}{EI}(\frac{x^3}{6}-\frac{Lx^2}{2})) |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
| Mathefix Verfasst am: 11. Jun 2020 20:12 Titel: |
|
|
|
Jetzt habe ich erkannt, dass es sich um einen einseitig eingespannten Balken handelt. |
|
|
ThisGuy
Gast
|
| ThisGuy Verfasst am: 11. Jun 2020 20:17 Titel: |
|
|
Es tut mir wirklich leid, aber ich verstehe das nicht.
Wenn  = P*(L-x)) ist, dann kann  = P*(L-0)) doch gar nicht gleich Null sein, außer die gegeben Kraft ist Null oder die Länge. Diese sind aber beide ungleich und größer Null.
Irgendetwas scheine ich zu übersehen... |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
| Myon Verfasst am: 11. Jun 2020 20:22 Titel: |
|
|
|
Nein, mein Fehler, entschuldige bitte die Verwirrung... bei der Einspannstelle ist das Drehmoment natürlich am grössten, M(0)=F*L. Beim Angriffspunkt der Kraft ist das Drehmoment =0. |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
| Mathefix Verfasst am: 11. Jun 2020 20:23 Titel: |
|
|
[quote="ThisGuy"]Es tut mir wirklich leid, aber ich verstehe das nicht.
Wenn ist, dann kann doch gar nicht gleich Null sein, außer die gegeben Kraft ist Null oder die Länge. Diese sind aber beide ungleich und größer Null.
An der Einspannstelle x = L ist das Biegemoment maximal
Jetzt M (x) zweimal integrieren ... hat Myon Dir schon abgenommen und für x = L und z = s einsetzen
= s = \frac{F_0}{EI}(\frac{L^3}{6}-\frac{L^3}{2}))
und Formel nach E umstellen. Das war's dann schon.
Wünsche ein entspanntes Wochenende und bleibt gesund.
Zuletzt bearbeitet von Mathefix am 11. Jun 2020 20:49, insgesamt 5-mal bearbeitet |
|
|
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5852
|
| Myon Verfasst am: 11. Jun 2020 20:25 Titel: |
|
|
|
Bin jetzt abwesend bis etwas 22 Uhr. Aber aus dem Verlauf von z(x) ergibt sich ja auch der „Biegepfeil“ s=z(L). Da s gegeben ist, lässt sich daraus E bestimmen. |
|
|
ThisGuy
Gast
|
| ThisGuy Verfasst am: 11. Jun 2020 21:00 Titel: |
|
|
Okay ich habe jetzt ein Ergebnis, auch wenn mich das alles immer noch ein wenig verwirrt.
Aber trotzdem, ich danke euch allen für die vielen Antworten. Schöne Feiertage euch allen!  |
|
|
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5863
Wohnort: jwd
|
| Mathefix Verfasst am: 12. Jun 2020 08:38 Titel: |
|
|
| ThisGuy hat Folgendes geschrieben: | Okay ich habe jetzt ein Ergebnis, auch wenn mich das alles immer noch ein wenig verwirrt.
Aber trotzdem, ich danke euch allen für die vielen Antworten. Schöne Feiertage euch allen! |
Wo hakt es denn? Du kannst mir auch eine PN schicken. |
|
|
|
Registrieren
Login
FAQ
Suchen
