| Autor |
Nachricht |
Ugur
Anmeldungsdatum: 31.10.2019
Beiträge: 13
|
 Ugur Verfasst am: 31. Okt 2019 15:20 Titel: Feldenergie(dichte) von el-mag.Feldern Ugur Verfasst am: 31. Okt 2019 15:20 Titel: Feldenergie(dichte) von el-mag.Feldern |
 |
|
Meine Frage:
Ich habe eine Frage zu einer Übungsaufgabe in Elektrodynamik.
->  \, \dd x ) , ,
wobei U die Feldenergie ist.
Wir sollen diesen Ausdruck erleiten aus ,
 \vec{B^2} ) ,(1)) , ,
wobei u die Feldenergiedichte ist .
 ist das skl.Potential des E-Feldes und ist das skl.Potential des E-Feldes und 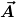 entsprechend das Vektor-Potenial des B-Feldes. entsprechend das Vektor-Potenial des B-Feldes.
Meine Ideen:
Ich hab zuerst das den Ausdruck  in in ^2 ) um geformt und dann mit der Poissongleichung bekommen das um geformt und dann mit der Poissongleichung bekommen das  *\varphi ) ist. Das passt denke ich mal da beim einsetzen in ist. Das passt denke ich mal da beim einsetzen in ) was raus kommt was für den ''E Part'' richtig aussieht. was raus kommt was für den ''E Part'' richtig aussieht.
Bei dem ''B Part'' habe ich das selbe mit dem Vektorportenial und der Poissongleichung für die Magentostatik versucht aber wenn ich ^2) mit dem selben Anstatz versuche zulösen bekomme ich beim umschreiben mit den Levi-Cevita-Symbolen mit dem selben Anstatz versuche zulösen bekomme ich beim umschreiben mit den Levi-Cevita-Symbolen  was neim einsetzen in (1)zu keinem richtigen Ergebniss führt. was neim einsetzen in (1)zu keinem richtigen Ergebniss führt. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 31. Okt 2019 16:14 Titel: jh8979 Verfasst am: 31. Okt 2019 16:14 Titel: |
 |
|
Levi-Civita-Symbole umschreiben und partielles Integrieren sollte sowas wie
^2 \sim (\Delta \vec A) \cdot \vec A - (\nabla \cdot \vec A)^2
<br />
)
liefern (modulo Vorzeichen, hab das mir gerade nur kurz skizziert).
Zuletzt bearbeitet von jh8979 am 01. Nov 2019 18:17, insgesamt einmal bearbeitet |
|
 |
Ugur1
Gast
|
 Ugur1 Verfasst am: 31. Okt 2019 23:08 Titel: Ugur1 Verfasst am: 31. Okt 2019 23:08 Titel: |
 |
|
|
Wieso den Partiell-Integrieren ? Kannst du das näher erklären , ich bin noch nicht so flüssig in Levi-Cevita- und Kronecker Delta Symbolen. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 31. Okt 2019 23:34 Titel: jh8979 Verfasst am: 31. Okt 2019 23:34 Titel: |
 |
|
Na wie passiert denn sonst diese Umformung??
| Zitat: |
 in in ^2 ) um geformt und dann mit der Poissongleichung bekommen das um geformt und dann mit der Poissongleichung bekommen das  *\varphi )
|
|
|
 |
Ugur2
Gast
|
 Ugur2 Verfasst am: 01. Nov 2019 09:52 Titel: Ugur2 Verfasst am: 01. Nov 2019 09:52 Titel: |
 |
|
|
Das hatte ich ohne Levi-Cevita-Symbole umgeformt..... |
|
 |
Ugur
Anmeldungsdatum: 31.10.2019
Beiträge: 13
|
 Ugur Verfasst am: 01. Nov 2019 12:34 Titel: Ugur Verfasst am: 01. Nov 2019 12:34 Titel: |
 |
|
| jh8979 hat Folgendes geschrieben: | Levi-Civita-Symbole umschreiben und partielles Integrieren sollte sowas wie
^2 \sim (\Delta \vec A) \cdot \vec A - (\nabla \cdot \vec A)^2
<br />
)
liefern (modulo Vorzeichen, hab das mir gerade nur kurz skizziert). |
Ich bin etwa verwirrt von dem ^2 ) es sollte doch es sollte doch ^2 ) sein oder ? sein oder ?
Das Vektor-Potential vom mag.Feld ist doch  |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 01. Nov 2019 16:41 Titel: index_razor Verfasst am: 01. Nov 2019 16:41 Titel: |
 |
|
Unter Vernachlässigung von Randtermen  komme ich auf komme ich auf
\dd V + \frac{1}{2}\int\left( \vec{A}\cdot\partial_t\vec{E} - \vec{E}\cdot\partial_t \vec{A}\right)\dd V.)
Ich sehe nicht, wie ich das zweite Integral wegdiskutieren kann. Habe ich mich verrechnet oder gilt die Aussage nur für statische Felder?
P.S.: In deinem Lösungsversuch hast du es selbst mit Magnetostatik versucht. Falls meine Vermutung also stimmt und es sich um zeitunabhängige Felder handelt, dann würde ich mal versuchen mit folgenden Vektoridentitäten einen Ansatz zu finden:
 = (\nabla\times \vec{A})\cdot\vec{B} - (\nabla \times\vec{B})\cdot\vec{A})
und
 = \nabla\cdot\vec{E}\phi + \nabla\phi\cdot\vec{E})
Zuletzt bearbeitet von index_razor am 01. Nov 2019 16:48, insgesamt einmal bearbeitet |
|
 |
Ugur
Anmeldungsdatum: 31.10.2019
Beiträge: 13
|
 Ugur Verfasst am: 01. Nov 2019 16:45 Titel: Ugur Verfasst am: 01. Nov 2019 16:45 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Unter Vernachlässigung von Randtermen  komme ich auf komme ich auf
\dd V + \frac{1}{2}\int\left( \vec{A}\cdot\partial_t\vec{E} - \vec{E}\cdot\partial_t \vec{A}\right)\dd V.)
Ich sehe nicht, wie ich das zweite Integral wegdiskutieren kann. Habe ich mich verrechnet oder gilt die Aussage nur für statische Felder? |
Ja es soll für statische und lokale Strom bzw. Ladungverteilung gelten .
Könntest du mir verraten was dein Ansatz war und wie du darauf gekommen bist damit ich es nachrechnen kann ? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 01. Nov 2019 16:48 Titel: index_razor Verfasst am: 01. Nov 2019 16:48 Titel: |
 |
|
|
Siehe meinen Edit aus dem letzten Beitrag. Die Produktregel auf Divergenzterme anzuwenden, die am Rand verschwinden, ist oft ein hilfreicher Trick. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 01. Nov 2019 18:16 Titel: jh8979 Verfasst am: 01. Nov 2019 18:16 Titel: |
 |
|
| Ugur hat Folgendes geschrieben: |
Ich bin etwa verwirrt von dem ^2 ) es sollte doch es sollte doch ^2 ) sein oder ? sein oder ?
Das Vektor-Potential vom mag.Feld ist doch  |
Ja, Tippfehler. Hab's korrigiert. |
|
 |
Ugur
Anmeldungsdatum: 31.10.2019
Beiträge: 13
|
 Ugur Verfasst am: 03. Nov 2019 10:53 Titel: Ugur Verfasst am: 03. Nov 2019 10:53 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | Unter Vernachlässigung von Randtermen  komme ich auf komme ich auf
\dd V + \frac{1}{2}\int\left( \vec{A}\cdot\partial_t\vec{E} - \vec{E}\cdot\partial_t \vec{A}\right)\dd V.)
Ich sehe nicht, wie ich das zweite Integral wegdiskutieren kann. Habe ich mich verrechnet oder gilt die Aussage nur für statische Felder?
P.S.: In deinem Lösungsversuch hast du es selbst mit Magnetostatik versucht. Falls meine Vermutung also stimmt und es sich um zeitunabhängige Felder handelt, dann würde ich mal versuchen mit folgenden Vektoridentitäten einen Ansatz zu finden:
 = (\nabla\times \vec{A})\cdot\vec{B} - (\nabla \times\vec{B})\cdot\vec{A})
und
 = \nabla\cdot\vec{E}\phi + \nabla\phi\cdot\vec{E}) |
Okay ich habs jetzt nach gerechnet aber bei dem B-Term
 = (\nabla\times \vec{A})\cdot\vec{B} - (\nabla \times\vec{B})\cdot\vec{A}) verschwindet bei mir nicht alles weil Rot(A) = B usw. verschwindet bei mir nicht alles weil Rot(A) = B usw. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Nov 2019 11:02 Titel: index_razor Verfasst am: 03. Nov 2019 11:02 Titel: |
 |
|
| Ugur hat Folgendes geschrieben: | | Zitat: |
 = (\nabla\times \vec{A})\cdot\vec{B} - (\nabla \times\vec{B})\cdot\vec{A})
und
 = \nabla\cdot\vec{E}\phi + \nabla\phi\cdot\vec{E}) |
Bei dem E-Feld Term kann ich das noch nachvollziehen aber bei dem B-Term weiß ich jetzt nicht woher das ) kommt. kommt.
|
Das war einfach mein Ansatz. Die Motivation kommt von dem Term \cdot\vec{B} ) auf der rechten Seite. Wenn du scharf hinschaust, erkennst du darin den Anteil des Magnetfeldes zur Energiedichte. Nun muß man nur die Rotation von A auf das B-Feld abwälzen. Dazu verwendet man immer irgendeine Produktregel. Mehr steckt nicht dahinter. auf der rechten Seite. Wenn du scharf hinschaust, erkennst du darin den Anteil des Magnetfeldes zur Energiedichte. Nun muß man nur die Rotation von A auf das B-Feld abwälzen. Dazu verwendet man immer irgendeine Produktregel. Mehr steckt nicht dahinter.
| Zitat: |
Wie formt man das in diese Form um ? |
In welche Form?
EDIT: Achso, du meinst das gesuchte Integral?
Schau dir nochmal die Produktregel für
)
genau an und setze alles was du über die Potentiale und Felder aus den Maxwellgleichungen etc. weißt, ein.
Zuletzt bearbeitet von index_razor am 03. Nov 2019 11:09, insgesamt einmal bearbeitet |
|
 |
Ugur
Anmeldungsdatum: 31.10.2019
Beiträge: 13
|
 Ugur Verfasst am: 03. Nov 2019 11:08 Titel: Ugur Verfasst am: 03. Nov 2019 11:08 Titel: |
 |
|
Jaa das hab ich jz auch aber bei dem linken Term von \cdot\vec{B} - (\nabla \times\vec{B})\cdot\vec{A}) steht bei mir dann steht bei mir dann  |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Nov 2019 11:10 Titel: index_razor Verfasst am: 03. Nov 2019 11:10 Titel: |
 |
|
|
Ich sehe das Problem nicht. Das ist doch genau was dabei rauskommen soll. Der Divergenzterm verschwindet im unendlichen. Ist es das, was du übersiehst? |
|
 |
Ugur
Anmeldungsdatum: 31.10.2019
Beiträge: 13
|
 Ugur Verfasst am: 03. Nov 2019 11:16 Titel: Ugur Verfasst am: 03. Nov 2019 11:16 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Ich sehe das Problem nicht. Das ist doch genau was dabei rauskommen soll. |
Ich suche ja jeweils einen Term der sogesehn das  und das und das 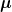 weg kürzt beim E Term geht das mit dem verteilen des nabla-terms ganz gut, aber beim B-feld kürzt sich beim einsetzen nicht alles weg ... Das B ^2 stört etwas weg kürzt beim E Term geht das mit dem verteilen des nabla-terms ganz gut, aber beim B-feld kürzt sich beim einsetzen nicht alles weg ... Das B ^2 stört etwas
 \vec{B^2} )) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Nov 2019 11:21 Titel: index_razor Verfasst am: 03. Nov 2019 11:21 Titel: |
 |
|
| Ugur hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Ich sehe das Problem nicht. Das ist doch genau was dabei rauskommen soll. |
Ich suche ja jeweils einen Term der sogesehn das  und das und das 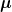 weg kürzt beim E Term geht das mit dem verteilen des nabla-terms ganz gut, aber beim B-feld kürzt sich beim einsetzen nicht alles weg ... Das B ^2 stört etwas weg kürzt beim E Term geht das mit dem verteilen des nabla-terms ganz gut, aber beim B-feld kürzt sich beim einsetzen nicht alles weg ... Das B ^2 stört etwas
|
Doch das kürzt sich weg. Teile  durch durch 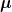 . Das ergibt die Energiedichte des Magnetfeldes. Dann setzt du die Identität ein, die du gerade hergeleitet hast und integrierst das ganze über den gesamten Raum. Schreib es am besten mal vollständig hin. . Das ergibt die Energiedichte des Magnetfeldes. Dann setzt du die Identität ein, die du gerade hergeleitet hast und integrierst das ganze über den gesamten Raum. Schreib es am besten mal vollständig hin.
Also:
\cdot \vec{B} = ...)
Ab hier gehts mit der Vektoridentität weiter. |
|
 |
Ugur
Anmeldungsdatum: 31.10.2019
Beiträge: 13
|
 Ugur Verfasst am: 03. Nov 2019 12:12 Titel: Ugur Verfasst am: 03. Nov 2019 12:12 Titel: |
 |
|
Also ... war das ziel darauf zukommen das  ist und ist und  ... ? ... ? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Nov 2019 12:17 Titel: index_razor Verfasst am: 03. Nov 2019 12:17 Titel: |
 |
|
| Ugur hat Folgendes geschrieben: | Also ... war das ziel darauf zukommen das  ist und ist und  ... ? ... ? |
Nein, du hast falsch eingesetzt. Nochmal zurück
\cdot \vec{B} = ...)
Nun wälzen wir die Rotation  von A auf B ab. Dazu verwenden wir die Produktregel von A auf B ab. Dazu verwenden wir die Produktregel
 = (\nabla\times \vec{A})\cdot\vec{B} - (\nabla \times\vec{B})\cdot\vec{A})
Nun einfach einsetzen und weiterrechnen...
P.S. Die Idee ist exakt dieselbe wie beim E-Feld. Nur die verwendete Produktregel ist eine andere. |
|
 |
Ugur
Anmeldungsdatum: 31.10.2019
Beiträge: 13
|
 Ugur Verfasst am: 03. Nov 2019 12:53 Titel: Ugur Verfasst am: 03. Nov 2019 12:53 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Ugur hat Folgendes geschrieben: | Also ... war das ziel darauf zukommen das  ist und ist und  ... ? ... ? |
\cdot \vec{B} = ...)
 = (\nabla\times \vec{A})\cdot\vec{B} - (\nabla \times\vec{B})\cdot\vec{A})
|
Irgendwie komme ich immer auf das selbe bin gerade zu doof dafür ...
wenn ich die Produktregel umforme in
\cdot\vec{B}= \nabla\cdot(\vec{A}\times\vec{B}) + (\nabla \times\vec{B})\cdot\vec{A})
komme ich auf
\cdot \vec{B} = \frac{1}{2\mu}(\nabla\cdot(\vec{A}\times\vec{B}) + (\nabla \times\vec{B})\cdot\vec{A})=\frac{1}{2\mu}( (\nabla\times \vec{A})\cdot\vec{B} - (\nabla \times\vec{B})\cdot\vec{A}+ (\nabla \times\vec{B})\cdot\vec{A})))
was kein sinn macht weil ich zu nix komme ..... was übersehe ich ? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Nov 2019 13:01 Titel: index_razor Verfasst am: 03. Nov 2019 13:01 Titel: |
 |
|
| Ugur hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Ugur hat Folgendes geschrieben: | Also ... war das ziel darauf zukommen das  ist und ist und  ... ? ... ? |
\cdot \vec{B} = ...)
 = (\nabla\times \vec{A})\cdot\vec{B} - (\nabla \times\vec{B})\cdot\vec{A})
|
Irgendwie komme ich immer auf das selbe bin gerade zu doof dafür ...
wenn ich die Produktregel umforme in
\cdot\vec{B}= \nabla\cdot(\vec{A}\times\vec{B}) + (\nabla \times\vec{B})\cdot\vec{A})
komme ich auf
\cdot \vec{B} = \frac{1}{2\mu}(\nabla\cdot(\vec{A}\times\vec{B}) + (\nabla \times\vec{B})\cdot\vec{A})=\frac{1}{2\mu}( (\nabla\times \vec{A})\cdot\vec{B} - (\nabla \times\vec{B})\cdot\vec{A}+ (\nabla \times\vec{B})\cdot\vec{A})))
was kein sinn macht weil ich zu nix komme ..... was übersehe ich ? |
Der letzte Schritt bringt natürlich nichts, weil du zweimal dieselbe Identität einsetzt. Dabei können nur Trivialitäten rauskommen. (Merke: bei jeder Umformung jede Identität nur einmal verwenden, ansonsten drehst du dich im Kreis.)
Bis hierhin sieht es aber schon mal gut aus
\cdot \vec{B} = \frac{1}{2\mu}(\nabla\cdot(\vec{A}\times\vec{B}) + (\nabla \times\vec{B})\cdot\vec{A})=...)
Wie kann es nun weitergehen? Vielleicht mit einer Maxwellgleichung. |
|
 |
Ugur
Anmeldungsdatum: 31.10.2019
Beiträge: 13
|
 Ugur Verfasst am: 03. Nov 2019 13:51 Titel: Ugur Verfasst am: 03. Nov 2019 13:51 Titel: |
 |
|
[quote="index_razor"][quote="Ugur"] | index_razor hat Folgendes geschrieben: |
Bis hierhin sieht es aber schon mal gut aus
\cdot \vec{B} = \frac{1}{2\mu}(\nabla\cdot(\vec{A}\times\vec{B}) + (\nabla \times\vec{B})\cdot\vec{A})=...)
Wie kann es nun weitergehen? Vielleicht mit einer Maxwellgleichung. |
Für \cdot\vec{A} ) bekomme ich die bekomme ich die * j*A ) also muss ja also muss ja  )
auch das selbe Ergebnis haben damit die beide 1/2 sich zu 1 addieren und dort nur  steht. steht.
Wenn ich für  ) , ,  einsetze komme ich auf einsetze komme ich auf * j*A ) also kommt wieder Null raus .... also kommt wieder Null raus .... |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Nov 2019 14:03 Titel: index_razor Verfasst am: 03. Nov 2019 14:03 Titel: |
 |
|
| Ugur hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Bis hierhin sieht es aber schon mal gut aus
\cdot \vec{B} = \frac{1}{2\mu}(\nabla\cdot(\vec{A}\times\vec{B}) + (\nabla \times\vec{B})\cdot\vec{A})=...)
Wie kann es nun weitergehen? Vielleicht mit einer Maxwellgleichung. |
Für \cdot\vec{A} ) bekomme ich die bekomme ich die * j*A ) also muss ja also muss ja  )
auch das selbe Ergebnis haben damit die beide 1/2 sich zu 1 addieren und dort nur  steht. steht.
|
Schau dir nochmal genau das Integral an, das du ableiten sollst. Der Vorfaktor 1/2 steht schon genau richtig da wo er ist.
Wir haben also
\cdot \vec{B} = \frac{1}{2\mu}(\nabla\cdot(\vec{A}\times\vec{B}) + (\nabla \times\vec{B})\cdot\vec{A})= \frac{1}{2\mu}\nabla\cdot(\vec{A}\times\vec{B}) + \frac{1}{2}\vec{j}\cdot\vec{A})
Nun fragst du dich vermutlich was mit der Divergenz von  passiert. Sagt dir der Gaußsche Integralsatz etwas? Damit kann man Volumenintegrale in Oberflächenintegrale umwandeln. Und über den Raum müssen wir ohnehin noch integrieren. passiert. Sagt dir der Gaußsche Integralsatz etwas? Damit kann man Volumenintegrale in Oberflächenintegrale umwandeln. Und über den Raum müssen wir ohnehin noch integrieren. |
|
 |
Ugur
Anmeldungsdatum: 31.10.2019
Beiträge: 13
|
 Ugur Verfasst am: 03. Nov 2019 14:39 Titel: Ugur Verfasst am: 03. Nov 2019 14:39 Titel: |
 |
|
[quote="index_razor"][quote="Ugur"] | index_razor hat Folgendes geschrieben: |
Nun fragst du dich vermutlich was mit der Divergenz von  passiert. Sagt dir der Gaußsche Integralsatz etwas? Damit kann man Volumenintegrale in Oberflächenintegrale umwandeln. Und über den Raum müssen wir ohnehin noch integrieren. passiert. Sagt dir der Gaußsche Integralsatz etwas? Damit kann man Volumenintegrale in Oberflächenintegrale umwandeln. Und über den Raum müssen wir ohnehin noch integrieren. |
So aus dem Stand würde ich sagen dass das Flächenintegral null sein muss weil dort keine Quellen sind.
Ich hab jetzt *\varphi +(1/2\mu ) \nabla(A \times B) + 1/2 * j* A \, \dd V ) und und
 \nabla(A \times B) ) sollte gleich null sein. sollte gleich null sein.
Mit dem Satz von Gauß für Integrale komme ich auf :
 \nabla(A \times B) \, \dd V = \int_\alpha ^{} \! (1/2\mu )(A \times B) \, \dd \alpha ) . .
Hier würde ich argumentieren das es halt keine Quellen gibt ... |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Nov 2019 14:56 Titel: index_razor Verfasst am: 03. Nov 2019 14:56 Titel: |
 |
|
| Ugur hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Nun fragst du dich vermutlich was mit der Divergenz von  passiert. Sagt dir der Gaußsche Integralsatz etwas? Damit kann man Volumenintegrale in Oberflächenintegrale umwandeln. Und über den Raum müssen wir ohnehin noch integrieren. passiert. Sagt dir der Gaußsche Integralsatz etwas? Damit kann man Volumenintegrale in Oberflächenintegrale umwandeln. Und über den Raum müssen wir ohnehin noch integrieren. |
So aus dem Stand würde ich sagen dass das Flächenintegral null sein muss weil dort keine Quellen sind.
Ich hab jetzt *\varphi +(1/2\mu ) \nabla(A \times B) + 1/2 * j* A \, \dd V ) und und
 \nabla(A \times B) ) sollte gleich null sein. sollte gleich null sein.
Mit dem Satz von Gauß für Integrale komme ich auf :
 \nabla(A \times B) \, \dd V = \int_\alpha ^{} \! (1/2\mu )(A \times B) \, \dd \alpha ) . .
Hier würde ich argumentieren das es halt keine Quellen gibt ... |
Wenn wir über den gesamten Raum integrieren, dann liegt die Oberfläche im Unendlichen. Das entscheidende ist nicht, das es dort keine Quellen gibt (obwohl das auch eine Rolle spielt), sondern daß das B-Feld hinreichend schnell im Unendlichen abfällt.
Heuristisch kann man, denke ich, argumentieren, daß dies hier der Fall ist, weil wir statische Felder betrachten. Die fallen mindestens mit  ab. Man kann also auch die Potentiale so eichen, daß sie im Unendlichen verschwinden. Für Strahlungsfelder würde das Argument wahrscheinlich nicht so einfach funktionieren. ab. Man kann also auch die Potentiale so eichen, daß sie im Unendlichen verschwinden. Für Strahlungsfelder würde das Argument wahrscheinlich nicht so einfach funktionieren.
Die elektrische Energie erfordert übrigens ein ganz ähnliches Argument. |
|
 |
Ugur
Anmeldungsdatum: 31.10.2019
Beiträge: 13
|
 Ugur Verfasst am: 03. Nov 2019 15:03 Titel: Ugur Verfasst am: 03. Nov 2019 15:03 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Ugur hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Nun fragst du dich vermutlich was mit der Divergenz von  passiert. Sagt dir der Gaußsche Integralsatz etwas? Damit kann man Volumenintegrale in Oberflächenintegrale umwandeln. Und über den Raum müssen wir ohnehin noch integrieren. passiert. Sagt dir der Gaußsche Integralsatz etwas? Damit kann man Volumenintegrale in Oberflächenintegrale umwandeln. Und über den Raum müssen wir ohnehin noch integrieren. |
So aus dem Stand würde ich sagen dass das Flächenintegral null sein muss weil dort keine Quellen sind.
Ich hab jetzt *\varphi +(1/2\mu ) \nabla(A \times B) + 1/2 * j* A \, \dd V ) und und
 \nabla(A \times B) ) sollte gleich null sein. sollte gleich null sein.
Mit dem Satz von Gauß für Integrale komme ich auf :
 \nabla(A \times B) \, \dd V = \int_\alpha ^{} \! (1/2\mu )(A \times B) \, \dd \alpha ) . .
Hier würde ich argumentieren das es halt keine Quellen gibt ... |
Wenn wir über den gesamten Raum integrieren, dann liegt die Oberfläche im Unendlichen. Das entscheidende ist nicht, das es dort keine Quellen gibt (obwohl das auch eine Rolle spielt), sondern daß das B-Feld hinreichend schnell im Unendlichen abfällt.
Heuristisch kann man, denke ich, argumentieren, daß dies hier der Fall ist, weil wir statische Felder betrachten. Die fallen mindestens mit  ab. Man kann also auch die Potentiale so eichen, daß sie im Unendlichen verschwinden. Für Strahlungsfelder würde das Argument wahrscheinlich nicht so einfach funktionieren. ab. Man kann also auch die Potentiale so eichen, daß sie im Unendlichen verschwinden. Für Strahlungsfelder würde das Argument wahrscheinlich nicht so einfach funktionieren.
Die elektrische Energie erfordert übrigens ein ganz ähnliches Argument. |
Stimmt ich hab ganz aus den Augen verloren das es um ein unendliches Volumen geht ..
Danke für deine Hilfe ! Ich glaube ich habs jetzt(endlich) verstanden .... |
|
 |
|















