| Autor |
Nachricht |
Thermomick's
Gast
|
 Thermomick's Verfasst am: 16. Okt 2019 18:23 Titel: Fermatsches Prinzip Verständnisfrage |
 |
|
Meine Frage:
Hallo, ich habe mir das fermatsche Prinzip angeschaut und habe sowohl die mathematischen Herleitungen über das Reflexionsgesetz als auch des Brechungsgesetzes verstanden. Aber bei Wikipedia finde ich folgende Aussage, die ich nicht nachvollziehen kann:
Das Fermatsche Prinzip (nach Pierre de Fermat) besagt, dass Licht in einem Medium zwischen zwei Punkten Wege nimmt, auf denen seine Laufzeit sich bei kleinen Variationen des Weges nicht ändert. Insbesondere ist die Optische Weglänge extremal, d. h. die längste oder kürzeste
Das die optische Weglänge extremal ist, leuchtet ein, da ja ein Minimum bezüglich der Laufzeit gesucht wird, deswegen wird hiernach auch abgeleitet, aber wieso ändern kleine Variationen des Weges die Laufzeit nicht???
Wenn ich bei der Brechung beispielsweise von einer ebenen Fläche ausgehe(zb bei der Brechung bei einer Wasseroberfläche) so ergibt die Ableitung nach der kürzesten Zeit genau ein Ergebnis!
Sollte ich jetzt mein x verschieben, dann verschiebt sich doch auch zwangsläufig die Laufzeit vom Minimum zu einem höheren Wert
Meine Ideen:
Ich kann mir nur vorstellen, dass gemeint sein soll, dass eine minimale Änderung der Weglänge eine gegen 0 konvergierende Änderung in Einfalls und Ausfallswinkel bewirkt. |
|
 |
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
| jh8979 Verfasst am: 16. Okt 2019 18:27 Titel: |
|
|
|
Gemeint ist das die Funktionalableitung bezüglich der Änderung des Weges verschwindet. Vllt bisschen salopp und ungünstig formuliert dort. |
|
|
Thermomick's
Gast
|
| Thermomick's Verfasst am: 16. Okt 2019 18:48 Titel: |
|
|
|
Sorry kannst du das etwas erleuchten, was du hier mit Funktionalableitung meinst? |
|
|
jh8979
Moderator
Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
| TomS Verfasst am: 16. Okt 2019 20:27 Titel: Re: Fermatsches Prinzip Verständnisfrage |
|
|
| Thermomick's hat Folgendes geschrieben: | | Das die optische Weglänge extremal ist, leuchtet ein, da ja ein Minimum bezüglich der Laufzeit gesucht wird, deswegen wird hiernach auch abgeleitet, aber wieso ändern kleine Variationen des Weges die Laufzeit nicht??? |
Um das Extremum einer Funktion f(x) zu finden, berechnest du die Ableitung und löst nach x d.h. für den Ort des Minimums auf:
}{\partial x} = 0 \;\to\; x_0)
Um das Extremum eines Funktionals F(y) zu finden, berechnest du die Funktionalbleitung und löst nach y auf:
)
y(x) ist dabei eine von x abhängige Funktion, F[y] ein Funktional, das der Funktion y einen Wert zuordnet.
Bsp.: wenn eine Geschwindigkeit v(t) gegeben ist, dann liefert das Funktional
)
den zurückgelegten Weg für jede eingesetzte Funktion v(t).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 18. Okt 2019 09:12 Titel: Re: Fermatsches Prinzip Verständnisfrage |
|
|
| Thermomick's hat Folgendes geschrieben: |
Das die optische Weglänge extremal ist, leuchtet ein, da ja ein Minimum bezüglich der Laufzeit gesucht wird, deswegen wird hiernach auch abgeleitet, aber wieso ändern kleine Variationen des Weges die Laufzeit nicht???
|
Gemeint ist, daß Änderungen des Weges x höchstens Änderungen zweiter Ordnung der Laufzeit t nach sich ziehen. Anders formuliert: die Änderungen der Laufzeit gehen schneller gegen null als die Änderungen der Wegstrecke. Oder noch anders formuliert: gegenüber kleinen Änderungen der Wegstrecke sind die Änderungen der Laufzeit vernachlässigbar.
Das ist ein ganz allgemeiner Zusammenhang: Für eine in x differenzierbare Funktion t gilt (Satz von Taylor)
 = t(x) + t'(x)h + O(|h|^2).)
Im Extremum ist  = 0) , also
 \approx t(x))
unter Vernachlässigung von Termen ) höherer Ordnung. Somit ändert sich die Zeit t im Minimum nicht (wesentlich) mit der Wegstrecke. |
|
|
Thermomick's
Gast
|
| Thermomick's Verfasst am: 18. Okt 2019 10:29 Titel: |
|
|
|
Vielen Dank, jetzt hab ichs... |
|
|
Thermonick's
Gast
|
| Thermonick's Verfasst am: 18. Okt 2019 19:21 Titel: |
|
|
Geht der Satz von Taylor eigentlich daraus hervor, dass die Funktionalableitung = 0 ist?
Die Funktionalableitung ergibt sich ja beim hamiltonschen Prinzip durch die Euler-Lagrange Gleichung . Wo ist die Verbundung zum Satz nach Taylor |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 18. Okt 2019 20:12 Titel: |
|
|
| Thermonick's hat Folgendes geschrieben: | Geht der Satz von Taylor eigentlich daraus hervor, dass die Funktionalableitung = 0 ist?
|
Nein, der Satz erfordert nur, daß die Funktion oder das Funktional mindestens n-mal ableitbar ist (n=1 in unserem Fall), nicht, daß die Ableitungen null sind.
| Zitat: |
Die Funktionalableitung ergibt sich ja beim hamiltonschen Prinzip durch die Euler-Lagrange Gleichung . Wo ist die Verbundung zum Satz nach Taylor |
Die Euler-Lagrange-Gleichung kommt ins Spiel, wenn das Funktional die spezielle Form eines Integrals über eine Lagrange-Funktion besitzt
, \dot x(t), t)\dd t.)
Wenn du die Differenz  bis zur ersten Ordnung in h ausrechnest, erhältst du (normalerweise sind nötige Randbedingungen an die Funktion h vorausgesetzt) als linearen Term ein Integral der Form
) h(t)\dd t + O(|h|^2),)
wobei
 = \frac{\partial L}{\partial x} - \frac{\dd}{\dd t}\frac{\partial L}{\partial \dot x})
die Euler-Lagrange-Ableitung von L ist.
Dieses Integral über ) h(t)) , aufgefaßt als lineares Funktional in h, ist nach dem Satz von Taylor die Funktionalableitung von S an der "Stelle" x, also
(x(t)) h(t)\dd t. )
Wenn x nun ein stationärer Punkt von S ist, dann muß
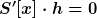
sein, und zwar für alle Funktionen h (evtl. mit den oben erwähnten Randbedingungen). Nach dem Hauptlemma der Variationsrechnung ist das nur möglich wenn
) = 0,)
also wenn die Euler-Lagrange-Gleichungen erfüllt sind. |
|
|
|
Registrieren
Login
FAQ
Suchen
