| Autor |
Nachricht |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 26. März 2019 13:41 Titel: Differenzieller Zusammenhang Stromstärke und Ladung Theoran Verfasst am: 26. März 2019 13:41 Titel: Differenzieller Zusammenhang Stromstärke und Ladung |
 |
|
Meine Frage:
Hallo zusammen,
ich bin ein absoluter Neuling auf physikerboard.de und habe eine Frage zu einer Aufgabenstellung aus der Elektrotechnik samt Lösung, die bei mir ein paar grundlegende Verständnisprobleme offengelegt hat.
Da ich mein Problem selber nicht richtig verstehe, seht es mir bitte nach, wenn meine Erklärung teilweise etwas wirr wirkt. Ich versuche, meine Gedankengänge so klar wie möglich zu erklären.
Die Aufgabe beschreibe ich hier und verlinke untenan zusätzlich zwei Fotos (Aufgabe und vorgegebene Lösung). Ich hoffe, dass meine Frage durch ihre Länge nicht gleich abschreckend wirkt und auch, dass mir jemand helfen kann.
Gefordert ist, eine allgemeine Lösung und drei spezielle Lösungen für die Ladungsmenge aufzustellen, die bei sich ändernder Stromstärke in einer gewissen Zeit fließt (Aufgabe 1.6.1).
Willkommen im Physikerboard!
Ich habe die beiden Bilder aus dem externen Link geholt, verkleinert und als Anhang eingefügt. Bitte verwende keine solchen Links, die sind irgendwann ungültig.
Viele Grüße
Steffen
Meine Ideen:
Nun zu meinem Verständnis der Aufgabe. Völlig klar ist, dass ich die Funktion in drei Abschnitte aufteilen muss
für 0 kleiner/gleich t kleiner/gleich 2
für 2 kleiner/gleich t kleiner/gleich 4
und für 4 kleiner/gleich t kleiner/gleich 6.
Nach meinem Verständnis ist die Ladungsmenge außerdem gleich der Fläche unterhalb der Funktion.
Und an dieser Stelle beginnt schon eines meiner Verständnisprobleme:
Die Formel für die Ladungsmenge erhalte ich aus
 (wenn I konstant ist), (wenn I konstant ist),
 oder oder
 . .
Erste Frage, die sich mir hier stellt: Wann wird aus  ein d und was drücke ich damit aus. ein d und was drücke ich damit aus.
Der erste Abschnitt ist eine lineare Funktion die doch die allgemeine Form
 hat. hat.
Die Stromstärke ist nicht konstant. Also nehme ich mir die Formel
 . .
Die stelle ich nach dem gesuchten Q um und erhalte
 \, \dd t ) . .
Zweite Frage: Warum hat mein Q an dieser stelle kein d mehr vorangestellt.
Jetzt aber zum Hauptproblem, das im Abschnitt drei noch viel wichtiger wird: Wie bringe ich diese Formel:
 \, \dd t )
jetzt in Einklang mit meiner allgemeinen Form
 . .
Klar ist mir, dass für den ersten Abschnitt mein y meinem Q(t) entspricht. Mein x müsste meiner Meinung nach meinem t entsprechen. Aber was sind m und n? Ist m gleich meinem i?
Der zweite Abschnitt müsste doch nach demselben Prinzip funktionieren, wie der erste, abgesehen davon, dass I konstant sein sollte. Deswegen gleich zum dritten Abschnitt, bei dem ich dann völlig aussteige.
Meine allgemeine Formel müsste ja wieder sein
 \, \dd t ) . .
Die Form der Kurve ist als quadratische Funktion vorgegeben. Also allgemein
 . .
Auch hier sollten mein y wieder gleich meinem Q(t) sein und mein x gleich meinem t. Aber was sind a, b und c?
Ich hoffe wirklich, wirklich sehr, dass trotz der vielleicht wirren Fragestellung jemand mein Problem erkennt, mir erklären kann, wo mein Denkfehler liegt und mir helfen kann, die Lösungen der Aufgabe nachzuvollziehen.
Vielen Dank und liebe Grüße
| Beschreibung: |
|
| Dateigröße: |
47.64 KB |
| Angeschaut: |
6713 mal |

|
| Beschreibung: |
|
| Dateigröße: |
40.79 KB |
| Angeschaut: |
6713 mal |
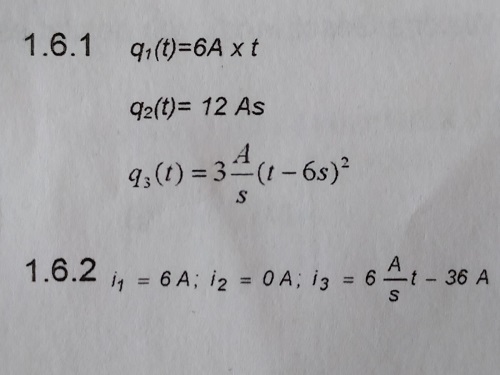
|
|
|
 |
PhyMaLehrer

Anmeldungsdatum: 17.10.2010
Beiträge: 1085
Wohnort: Leipzig
|
 PhyMaLehrer Verfasst am: 26. März 2019 14:36 Titel: PhyMaLehrer Verfasst am: 26. März 2019 14:36 Titel: |
 |
|
"Die Fläche unter der Kurve ist gleich der Ladungsmenge" trifft zu für ein Stromstärke-Zeit-Diagramm. Hier ist aber auf der y-Achse nicht die Stromstärke, sondern die Ladungsmenge selbst aufgetragen!
Einfachster Abschnitt: Im Bereich 2 s bis 4 s bleibt die Ladungsmenge wie festgenagelt bei 12 As, nichts kommt hinzu und nichts verschwindet. Wie groß ist dann also der Strom in diesem Abschnitt?
Zweiteinfachster  Abschnitt: Zwischen 0 und 2 s nimmt die Ladungsmenge gleichmäßig von 0 bis zum Wert von 12 As zu. Abschnitt: Zwischen 0 und 2 s nimmt die Ladungsmenge gleichmäßig von 0 bis zum Wert von 12 As zu.
Man nimmt ja gern das Modell eines Wasserstroms zu Hilfe: Wenn die Wassermenge in einem Meßzylinder innerhalb von 2 s gleichmäßig von 0 bis auf 12 cm³ zunimmt, was bedeutet das (qualitativ) für die Stärke des Zuflusses? Und wie groß ist dieser (Wasser-) Strom dann in cm³/s?
Und zurück zum elektrischen Strom: Wie ist der Strom beschaffen, der die transportierte Ladungsmenge in 2 s gleichmäßig auf 12 As anwachsen läßt?
(Das ist jetzt vielleicht sehr umständlich erklärt; eigentlich sieht man es auf den ersten oder mindestens auf den zweiten Blick. Und du siehst es auch, wenn du es verstanden hast!  ) )
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 27. März 2019 13:01 Titel: Theoran Verfasst am: 27. März 2019 13:01 Titel: |
 |
|
Danke für deine Antwort PhyMaLehrer. Ich würde meine Gedanken/Rückschlüsse dazu einfach mal Absatz für Absatz beschreiben.
Wenn die Fläche unter der Kurve bei einem Stromstärke-Zeit-Diagramm der Ladungsmenge entspricht, kann ich dann den Rückschluss ziehen, dass die Fläche unter der Kurve bei einem Ladungsmenge-Zeit-Diagramm der Stromstärke entspricht?
Im zweiten Abschnitt (2 s bis 4 s) bleibt die Ladungsmenge dauerhaft bei 12 As. Daraus würde doch folgen, dass in dieser Zeit kein Strom fließt und die Stromstärke damit 0 ist. Wenn das zutrifft, wäre meine erste Schlussfolgerung (Stromstärke gleich Fläche unter der Kurve) aber schon falsch. Außerdem passt eine Stromstärke von 0 ja nicht zur Formel I=Q/t. 0 ist ja nicht gleich 12As/2s. Oder zähle ich für jeden Abschnitt Q wieder von 0 an?
Für den Abschnitt 0 s bis 2 s:
Aus deinem Beispiel mit dem Wasserstrom würde doch hier gelten:
Innerhalb von zwei Sekunden erreiche ich 12 As an Ladung. Das heißt, dass die Stromstärke zu jeder Sekunde 6 Ampere beträgt.
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 27. März 2019 13:27 Titel: Steffen Bühler Verfasst am: 27. März 2019 13:27 Titel: |
 |
|
| Theoran hat Folgendes geschrieben: | | Wenn die Fläche unter der Kurve bei einem Stromstärke-Zeit-Diagramm der Ladungsmenge entspricht, kann ich dann den Rückschluss ziehen, dass die Fläche unter der Kurve bei einem Ladungsmenge-Zeit-Diagramm der Stromstärke entspricht? |
Nein. Nach dem Fundamentalsatz der Analysis entspricht die Stromstärke der Steigung des Ladungsverlaufs.
Viele Grüße
Steffen
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 28. März 2019 12:49 Titel: Theoran Verfasst am: 28. März 2019 12:49 Titel: |
 |
|
Danke Steffen,
ein sehr guter Hinweis. Ich kann aus dem Artikel und den Videos zum Hauptsatz der Integral- und Differentialrechnung noch nicht ableiten, warum die Steigung gleich der Stromstärke entspricht.
Aber ich kann aus Deiner Aussage ja ableiten, dass die Allgemeine Form y = mx + n dann dann sozusagen Q = i * t + n entspricht, richtig?
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 28. März 2019 13:15 Titel: Steffen Bühler Verfasst am: 28. März 2019 13:15 Titel: |
 |
|
Richtig, und auch hier entspricht die Steigung m eben der Stromstärke i.
Die Ladung steigt ja hier in zwei Sekunden konstant von Null auf 12As. Das ergibt also eine konstante Steigung und damit einen konstanten Strom von 
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 28. März 2019 13:34 Titel: Theoran Verfasst am: 28. März 2019 13:34 Titel: |
 |
|
Demnach ergibt sich Q = 6 * t + n (mit n = 0), da der Schnittpunkt mit der Q-Achse bei 0 liegt.
Dann zum zweiten Abschnitt. Wieder eine lineare Funktion der Form y = m * x + n oder im konkreten Beispiel Q = i * t + n. Nun ist nach der Erklärung von PhyMaLehrer ja aber i in diesem Abschnitt 0 (wenn ich seine Erklärung richtig gedeutet habe). Also müsste doch gelten: 12 As = 0 * t + n.
Das kann aber nur der Fall sein, wenn mein n = 12 ist. Wo kommen in diesem Fall dann aber die As her? Bleibt die Einheit trotz der Multiplikation mit 0 erhalten?
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 28. März 2019 13:41 Titel: Steffen Bühler Verfasst am: 28. März 2019 13:41 Titel: |
 |
|
Die Null wird ja nur zum t multipliziert, nicht zum n. Und in der Tat ist n=12As.
Nachtrag: wir sind hier eben in der Physik, da hat alles eine Einheit. Auch die vorherige Gleichung muss also korrekt lauten =6 A \cdot t)
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 28. März 2019 13:52 Titel: Theoran Verfasst am: 28. März 2019 13:52 Titel: |
 |
|
Also bleibt die Einheit bestehen, vielen Dank. Ich habe nur überhaupt keine Idee für den letzten Abschnitt.
Was ich suche, ist eine Gleichung für die Ladungsmenge. Die wiederum entspricht meiner Fläche unter der Kurve. Die Formel müsste also lauten:
 \, \dd x ) . .
Die Kurve hat laut Aufgabe die Form einer quadratischen Parabel. Also allgemein
 . .
Aber auch hier fehlt mir wieder das Verständnis, die Formeln zusammenzubringen. Auch hier ist mir wieder klar: y entspricht meinem Q und x meinem t.
Meine Idee war erst einmal, zwei Formel Aufzustellen.
 = 12 As = a * 4s² + b * 4s + c )
und
 = 0 As = a * 6s² + b * 6s + c )
Aber nach diesem Ansatz (sofern es den der richtige ist) bekomme ich die Formeln nicht mit
 \, \dd x )
zusammen
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 28. März 2019 14:08 Titel: Steffen Bühler Verfasst am: 28. März 2019 14:08 Titel: |
 |
|
Wie ja schon geschrieben, ist die Ladungsmenge nicht die Fläche unter der Kurve, sondern die Kurve selber. Daher brauchst Du Dich hier nicht mit einem Integral rumzuärgern, nur mit der Steigung, also mit Ableitungen.
Diese Parabel läuft, wie man der Zeichnung entnehmen kann, genau in die x-Achse "rein", sie hat also ihren Tiefpunkt bei t=6s. Und damit bekommst Du die dritte Gleichung, die Du für die drei Unbekannten brauchst.
Vorsicht übrigens beim Aufstellen: wenn Du z.B. die Zeit 4s quadrierst, entstehen nicht 4s², sondern 16s².
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 31. März 2019 14:40 Titel: Theoran Verfasst am: 31. März 2019 14:40 Titel: |
 |
|
|
Kannst Du mir bitte nochmal genau erklären, wie genau Du erkennen kannst, welche Größe Du wo aus diesem System ablesen kannst? Mit anderen Worten: Woher weißt Du, dass im Beispiel i = der Anstieg ist, Q gleich die Gleichung usw.
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 31. März 2019 14:53 Titel: Steffen Bühler Verfasst am: 31. März 2019 14:53 Titel: |
 |
|
Versuch es Dir mal praktisch vorzustellen. Du hast einen Akku mit 12 Ah Kapazität und lädst den auf. Zuerst ist er leer, aber er wird kontinuierlich voller, bis nach 2 Stunden nichts mehr reingeht.
Die Ladung könntest Du Dir als eine Riesenmenge Elektronen vorstellen, was ja auch stimmt. Noch anschaulicher vielleicht als Tischtennisbälle. Beim Aufladen fällt also ein solcher Ball nach dem anderen in den Akku, den Du Dir als Badewanne vorstellen kannst.
Der elektrische Strom ist nun in diesem Modell die Fließgeschwindigkeit der Tischtennisbälle. Also Bälle pro Zeit. Denn Ladung pro Zeit ist Strom. Wenn die Wanne in einer Stunde voll sein muss, müssen die Bälle schneller fließen als wenn zwei Stunden dafür Zeit ist. Der Strom müsste dann doppelt so groß sein.
Wenn Du das nun in eine Ladekurve zeichnest, also die Anzahl der Bälle über der Zeit, wird die Kurve im ersten Fall steiler ansteigen als im zweiten. Und wenn Du die Steigung nachrechnest, wird sie doppelt so groß sein.
Das heißt also, wenn Du ein Lineal an die Kurve legst, erhältst Du mit der Steigung den momentan fließenden Strom. Also Ladung durch Zeit, und eine Division entspricht ja einer Steigung, genau wie das Integrieren einer Multiplikation entspricht.
Leichter ist es vielleicht, statt Ladung hier eine Strecke zu nehmen. Dann ist es vielleicht klarer, dass die Steigung der Geschwindigkeit entspricht. Du kannst das ja spaßeshalber mit dieser Kurve auch tun. Da läuft jemand gleichmäßig schnell auf einen 12 Meter hohen Berg, bleibt dort eine Weile und läuft dann wieder runter, zuerst schnell, dann langsamer.
Viele Grüße
Steffen
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 31. März 2019 15:05 Titel: Theoran Verfasst am: 31. März 2019 15:05 Titel: |
 |
|
Hallo Steffen,
vielen Dank für Deine Antwort. Du hast sehr anschaulich erklärt, welche was sich hinter den einzelnen Größen verbirgt und wie ich sie mir vorstellen muss. Und zumindest für dieses Beispiel kann ich die Größen damit zu großen Teilen dem Graphen zuordnen.
Dennoch habe ich auch zu Deiner Antwort ein paar konkrete Fragen.Wie bereits gesagt, kann ich mir für dieses Beispiel die Größen vorstellen. Aber gibt es eine allgemeine Regel, die ich anwenden kann, um zu erkennen, was wo wie steht? Wenn ich z.B. Ladung und Stromstärke tausche, also die Ladung an die Y-Achse schreibe. Oder wie in Deinem zweiten Beispiel, wenn ich Weg und Geschwindigkeit tausche.
In Bezug auf die Aufgabe stellen sich mir außerdem immer noch ein Fragen zum letzten Teil der Kurve. Einerseits wüsste ich gerne, was denn die Fläche unter den Kurven nun darstellt? Wenn ich die ganze Geschichte integrieren würde (auch wenn ich es nicht muss), was würde ich dann erhalten? Außerdem würde ich nach wie vor gerne verstehen, wie die Gleichung

in Einklang mit meiner Ableitungsformel steht.
dt )
Mein c bleibt sicher mein Schnittpunkt mit der y-Achse. Aber was sind a und b?
Und meine letzte Frage bezieht sich auf den Zusammenhang, den Du im vorletzten Absatz beschreibst:
" Also Ladung durch Zeit, und eine Division entspricht ja einer Steigung, genau wie das Integrieren einer Multiplikation entspricht."
Das erschließt sich mir leider überhaupt nicht.
Ich weiß, viele Fragen und ich möchte mich auch nicht dümmer anstellen, als viele andere. Aber mir fehlt wirklich noch das Verständnis.
Liebe Grüße
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 31. März 2019 15:09 Titel: Steffen Bühler Verfasst am: 31. März 2019 15:09 Titel: |
 |
|
Wie man die Parabel über ein Gleichungssystem bestimmt, hatte ich ja schon angedeutet, das ist eine sogenannte Steckbriefaufgabe aus der Mathematik. Können wir dann aber auch gerne detaillierter besprechen.
Dass Integrieren dem Multiplizieren entspricht und Differenzieren dem Dividieren, diese Erkenntnis ist wohl die Crux des Ganzen. Ich glaube, wenn Dir das aufgeht, ist der Rest kein Problem mehr.
Denn Geschwindigkeit ist Weg durch Zeit. In einem Weg-Zeit-Diagramm (male Dir eins auf!) also die Steigung der (im einfachsten Fall geraden) Linie. Die Kurve kann aber auch wild rauf- und runtergehen, die Aussage gilt für jeden einzelnen Punkt immer noch! Nur dass man dann ja einen sehr kleinen Wegabschnitt durch einen sehr kleinen Zeitabschnitt teilt, also eigentlich durch Null dividieren müsste. Dieses Paradoxon (siehe Zeno) hat die Mathematiker lange gequält, erst Newton und Leibniz konnten sie mit der Analysis erlösen. Und seitdem wissen wir, dass wir den Weg einfach ableiten müssen, um die momentane Geschwindigkeit zu erhalten.
Umgekehrt ist Weg das Produkt aus Geschwindigkeit und Zeit. Immer, auch wenn die Geschwindigkeit nicht konstant ist und das v-t-Diagramm (mal Dir auch welche auf!) also kein Rechteck ist. Egal, was die Geschwindigkeit im Diagramm macht, rauf, runter, positiv, negativ, ihr Integral ist immer der zurückgelegte Weg.
Den Weg wiederum zu integrieren, ist zwar mathematisch möglich, aber physikalisch sinnfrei. Es ergäbe sich ein Wert in Meter mal Sekunde, mit dem niemand was anfangen kann. Dasselbe gilt für die Ladung. Die Fläche unter Q(t) ist aussagelos. Man könnte sie berechnen und in Ampere mal Quadratsekunde angeben, aber das Ergebnis ist uninteressant.
Viele Grüße
Steffen
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 31. März 2019 15:47 Titel: Theoran Verfasst am: 31. März 2019 15:47 Titel: |
 |
|
Ich hoffe so sehr, dass ich Dich jetzt richtig verstanden habe und das Folgende korrekt ist. In einem v-t-Diagramm ist die Fläche unter der Kurve der Weg. Denn es gilt:

(Multiplikation = Integration).
Folgt dann daraus, dass die Steigung einer Kurve an einer Stelle in diesem v-t-Diagramm der Beschleunigung entspricht? Denn es gilt ja:

(Division = Ableitung)
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 31. März 2019 16:45 Titel: Steffen Bühler Verfasst am: 31. März 2019 16:45 Titel: |
 |
|
|
Ja, das ist völlig korrekt.
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 31. März 2019 18:14 Titel: Theoran Verfasst am: 31. März 2019 18:14 Titel: |
 |
|
Perfekt, dann ist dieser Teil klar. Nun fehlt mir aber noch das Verständnis für die allgemeinen Formeln und die speziellen. Im Beispiel habe ich ja im letzten Abschnitt eine Funktion zweiten Grades. Es ist ja aber nicht ausgeschlossen, dass die auch mal dritten Grades o.Ä. ist.
Wie bringe ich diese Formeln zusammen. Also egal ob

oder
 . .
Beide allgemeinen Formen müssen ja irgendwie mit den anderen Formeln zusammenpassen.
Nach meinem jetzigen Verständnis versteckt sich im speziellen Fall hinter der gesamten Formel mein i. Sodass im Beispiel gelten würde:
dt ) (allgemein) (allgemein)
 (für i) (für i)
 dt )
(als Kombination aus allgemein und speziell)
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 31. März 2019 19:11 Titel: Steffen Bühler Verfasst am: 31. März 2019 19:11 Titel: |
 |
|
Wenn i(t) gegeben ist und q(t) gesucht wird, musst Du integrieren, z.B. (mal ohne Einheiten):
=3\cos t + 4t \to q(t)=3 \sin t +2t^2)
Im Beispiel ist nun q(t) als Funktion zweiten Grades gegeben und i(t) ist gesucht. Hier wird also abgeleitet:
=at^2+bt+c \to i(t)=2at +b)
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 31. März 2019 21:36 Titel: Theoran Verfasst am: 31. März 2019 21:36 Titel: |
 |
|
|
Ok, ich bin jetzt nicht ganz sicher, ob Du meiner Erklärung zugestimmt hast oder ob ich einen Fehler hatte.
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 01. Apr 2019 07:27 Titel: Steffen Bühler Verfasst am: 01. Apr 2019 07:27 Titel: |
 |
|
Du hast zweimal die Integralzeichen vergessen, darauf wollte ich jetzt nicht eingehen.
Und dann scheinst Du immer noch der Ansicht zu sein, dass in der Aufgabe der Stromverlauf i(t) als Funktion zweiten Grades gegeben ist, und nun q(t) gesucht wird. Es ist aber genau umgekehrt: q(t) ist doch gegeben!
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 02. Apr 2019 22:08 Titel: Theoran Verfasst am: 02. Apr 2019 22:08 Titel: |
 |
|
Beschränken wir uns mal auf den letzten Abschnitt, um alle verbleibenden Probleme auszuräumen (auch auf die Gefahr hin, dass ich jetzt in die völlig falsche Richtung gehe). Ich schreibe jetzt mal wirklich jeden Zwischenschritt zu meinem Denken auf.
Gesucht ist eine allgemeine Formel für q(t), also Ladung pro Zeit für den vorliegenden Fall. Meine Funktion Q(t) hat im letzten Abschnitt die allgemeine Form einer quadratischen Funktion.
 = at² + bt + c )
Soweit sollte alles richtig sein. Die allgemeine Formel für Q ist:
 \, \dd t )
In einem i/t-Diagramm wären die Grenzen a und b des Integrals wichtig, da dort die Fläche unter der Kurve meiner Ladung entsprechen würde, wenn ich jetzt nicht völlig daneben liege. Im vorliegenden Fall würde ich die Integrale aber unbestimmt lassen, da Q(t) ja meine reine Stammfunktion ist und ich nicht die Fläche unter der Kurve errechnen möchte (wenigstens soviel ist mittlerweile klar).
Es muss meiner Ansicht nach ja weiterhin/außerdem gelten:
 \, \dd t )
Was mir nun fehlt, sind a, b und c und i. Für die Stromstärke gilt:

Die Division entspricht dem Ableiten, woraus folgt, dass ich Q(t) nach t ableiten (wie Du in deiner letzten Nachricht schon gezeigt hast).
 = at² + bt + c \, \dd t = 2at + b )
Gesamt ergibt sich dann also erst einmal:

Erst einmal bis zu dieser Stelle. Bis hierher sollte doch kein Denkfehler mehr sein, richtig?
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 03. Apr 2019 07:18 Titel: Steffen Bühler Verfasst am: 03. Apr 2019 07:18 Titel: |
 |
|
|
Ja, das passt alles. Nun bestimme a, b und c.
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 03. Apr 2019 13:36 Titel: GvC Verfasst am: 03. Apr 2019 13:36 Titel: |
 |
|
| Steffen Bühler hat Folgendes geschrieben: | | Ja, das passt alles. |
Na ja, alles stimmt so nicht.
| Theoran hat Folgendes geschrieben: | ...

... |
Das gilt nur für den Spezialfall eines konstanten Stromes. Ganz allgemein gilt (einschließlich des Falles eines konstanten Stromes)
=\frac{\dd Q}{\dd t})
Das ist übrigens der wesentliche Zusammenhang zur Bearbeitung dieser Aufgabe.
Auch das hier ist nicht richtig:
| Theoran hat Folgendes geschrieben: | ...
 = at² + bt + c \, \dd t = 2at + b )
... |
Richtig wäre
=\frac{\dd}{\dd t}\left(at^2+bt+c\right)= ...)
Und hier fehlen Klammern (in rot hinzugefügt):
| Theoran hat Folgendes geschrieben: | ...
}\dd t )
... |
| Steffen Bühler hat Folgendes geschrieben: | | Nun bestimme a, b und c. |
Das ist zwar prinzipiell richtig, führt aber möglicherweise auf den Umweg, die drei Koeffizienten mit Hilfe dreier Gleichungen zu bestimmen (zwei bekannte Funktionswerte Q(4s) und Q(6s) sowie ein bekannter Ableitungswert i(6s)). Da der Scheitelpunkt der Parabel aber bekannt ist, lässt sich die Scheitelform der Parabelgleichung sofort hinschreiben, in der nur noch der Koeffizient a als Unbekannte auftaucht, die sich dann aus der Gleichung für Q(4s) leicht bestimmen lässt.
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 03. Apr 2019 14:49 Titel: Steffen Bühler Verfasst am: 03. Apr 2019 14:49 Titel: |
 |
|
| GvC hat Folgendes geschrieben: | | Steffen Bühler hat Folgendes geschrieben: | | Nun bestimme a, b und c. |
Das ist zwar prinzipiell richtig, führt aber möglicherweise auf den Umweg, die drei Koeffizienten mit Hilfe dreier Gleichungen zu bestimmen |
Dies war allerdings Theorans anfängliche Frage. Ihn davon abzubringen und mit der Scheitelpunktform anzufangen (mag sie auch leichter sein), verwirrt ihn wahrscheinlich zusätzlich. Daher würde ich aus Didaktikgründen den vorgeschlagenen Weg gehen.
Theoran, wenn Dir die Scheitelpunktform bekannt ist, kannst Du natürlich auch damit rechnen.
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 03. Apr 2019 15:00 Titel: GvC Verfasst am: 03. Apr 2019 15:00 Titel: |
 |
|
@Steffen Bühler
Du hast natürlich vollkommen recht. Ich wollte mit meinem Vorschlag - als zusätzliche Info sozusagen - nur die Verbindung zur Musterlösung herstellen, die ja genau als Scheitelform der gegebenen Parabelgleichung formuliert ist. Das hätte ich vielleicht explizit erwähnen sollen. Sorry.
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 04. Apr 2019 20:01 Titel: Theoran Verfasst am: 04. Apr 2019 20:01 Titel: |
 |
|
Hallo Steffen und GvC,
habt vielen Dank für Eure Antworten. Ich würde das Ganze gerne weiter so wie in meinem letzten Post fortsetzen - also jeden Schritt, den ich im Kopf mache, hier aufschreiben.
Vorweg: Die Dinge, die Du angebracht hast, GvC (abgesehen von der Scheitelpunktform) sind doch in erster Linie "Schreibfehler" richtig?
Nun zur Fortsetzung der Aufgabe. Erst einmal auf dem Weg, den ich begonnen habe, denn dabei komme ich sehr schnell zu einem Problem.
Ich stelle nun also Drei Gleichungen auf (erst einmal ohne Einheiten):



Diese drei Gleichungen sind meine Basis für meine Rechnung. Und ich glaube, jetzt mache ich schon einen Fehler. Ich würde mir erstmal die dritte Gleichung hernehmen und nach b umstellen:

Erstmal die Frage: Liegt hier schon ein Fehler?
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 05. Apr 2019 03:21 Titel: GvC Verfasst am: 05. Apr 2019 03:21 Titel: |
 |
|
| Theoran hat Folgendes geschrieben: | | Die Dinge, die Du angebracht hast, GvC (abgesehen von der Scheitelpunktform) sind doch in erster Linie "Schreibfehler" richtig? |
Das kann man so sehen. Allerdings zeigen sie auch, dass Du mit der Mathematik irgendwie auf Kriegsfuß stehst oder - noch schlimmer - nicht wirklich verstehst, was diese "Dinge" bedeuten.
| Theoran hat Folgendes geschrieben: | | Erstmal die Frage: Liegt hier schon ein Fehler? |
Nein. Bislang alles richtig. Ich würde allerdings die Einheiten nicht vernachlässigen. Sie erleichtern die Kontrolle.
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 09. Apr 2019 12:47 Titel: Theoran Verfasst am: 09. Apr 2019 12:47 Titel: |
 |
|
Danke GvC,
entschuldige bitte, dass ich solange nicht auf Deine Antwort eingegangen bin. Ich würde jetzt an der Stelle ansetzen, an der ich beim letzten Mal aufgehört habe.
Ich habe also jetzt meine beiden ersten Gleichungen:


und meinen Wert für b:
 . .
Letzteres setzte ich jetzt in meine zweite Gleichung ein, stelle sie nach c um und erhalte:
 + c \rightarrow 0 = -36a + c \rightarrow c = 36a)
Mit meinem Wert für c gehe ich jetzt zur ersten Gleichung und setzte b und c dort ein:
 + 36a \rightarrow 12 = 4a \rightarrow a = 3)
Daraus kann ich b und c einfach ermitteln:


Daraus wiederum würde für Q(t) folgne:
 = 3t² -36t + 108)
Erst einmal bis zu dieser Stelle mit der Frage, ob ein Fehler passiert ist?
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 09. Apr 2019 13:45 Titel: Steffen Bühler Verfasst am: 09. Apr 2019 13:45 Titel: |
 |
|
|
Offenbar nicht, denn das entspricht der ausmultiplizierten Musterlösung (wenn Du die Einheiten wie empfohlen dazunimmst).
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 09. Apr 2019 13:58 Titel: GvC Verfasst am: 09. Apr 2019 13:58 Titel: |
 |
|
@Theoran
Wie gesagt, es fehlen die Einheiten. In einer Physik-Klausur gäbe das Punktabzug.
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 11. Apr 2019 09:14 Titel: Theoran Verfasst am: 11. Apr 2019 09:14 Titel: |
 |
|
Ja, Du hast recht. Dann hier nochmal die Korrektur mit Einheiten:



sind meine beiden Gleichungen bzw. mein b. Weiter mit dem Einsetzen:
 + c \rightarrow 0As = -36a * s² + c \rightarrow c = 36a * s² )
Mein Wert für c in die erste Gleichung:
 + 36a * s² \rightarrow 12As = 4a * s² \rightarrow a = 3 * s)
Und daraus jetzt b und c ermittelt:


Es war gut, dass Du nochmal auf die Einheiten gepocht hast. Denn ich glaube, hier habe ich noch einen Denkfehler. Denn a, b und c müssten doch am Ende eigentlich einheitenlos sein oder nicht?
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 11. Apr 2019 09:42 Titel: Steffen Bühler Verfasst am: 11. Apr 2019 09:42 Titel: |
 |
|
Nein, im Gegenteil! Aus der in der Aufgabe genannten Ursprungsgleichung =a \cdot t^2+b \cdot t + c) folgt doch zunächst, dass links die Einheit As stehen muss. Da t in Sekunden angegeben wird, muss a zwangsläufig die Einheit folgt doch zunächst, dass links die Einheit As stehen muss. Da t in Sekunden angegeben wird, muss a zwangsläufig die Einheit  haben, b die Einheit haben, b die Einheit  und c die Einheit und c die Einheit 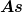 . .
In Deiner Korrektur ist aber auf einmal das t verschwunden, das hast Du durch s ersetzt. Das ist falsch, das t muss eben rechts bleiben. Es hat in der Tat die Einheit Sekunde, bei Dir ist es aber dadurch fest auf den Wert 1s gezurrt, das ist hier sinnlos, Du willst ja eine zeitabhängige Gleichung, eben Q(t) und nicht Q(1s).
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 11. Apr 2019 09:55 Titel: Theoran Verfasst am: 11. Apr 2019 09:55 Titel: |
 |
|
Also wäre die Korrektur - beispielhaft für die erste Gleichung - s in t zu ändern (und damit variabel zu machen) und an c As anzuhängen. Also:

Noch ein Nachtrag, um sicherzugehen, dass ich verstanden habe, was Du geschrieben hast. Hätten wir eine Gleichung dritten Grades müssten die Einheiten wie folgt aussehen:

Zuletzt bearbeitet von Theoran am 11. Apr 2019 10:02, insgesamt einmal bearbeitet |
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 11. Apr 2019 10:00 Titel: Steffen Bühler Verfasst am: 11. Apr 2019 10:00 Titel: |
 |
|
Ja, oder alternativ davon auszugehen, dass z.B. c in As angegeben wird, so wie "man ja auch weiß", dass t in s angegeben wird.
PS: aber Dein Ansatz ist wahrscheinlich "sicherer"
PPS: Dein Ansatz dritter Ordnung ist auch korrekt.
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 11. Apr 2019 10:20 Titel: Theoran Verfasst am: 11. Apr 2019 10:20 Titel: |
 |
|
Ok perfekt. Dann ergibt sich folgende Formel für Ladungsmenge Q(t):
 = 3 \frac{A}{s}t² -36At + 108 As )
und für i(t):
 = 6 \frac{A}{s}t -36A )
Jetzt ist mir aber nicht ganz klar, wie ich an dieser Stelle weitermachen muss.
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 11. Apr 2019 10:26 Titel: Steffen Bühler Verfasst am: 11. Apr 2019 10:26 Titel: |
 |
|
|
Du bist doch fertig! Du hast die drei Gleichungen für q(t) bestimmt, genauso für i(t). Das noch geforderte grafische Darstellen des Stroms sollte keine Schwierigkeiten mehr machen.
|
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
 GvC Verfasst am: 11. Apr 2019 10:29 Titel: GvC Verfasst am: 11. Apr 2019 10:29 Titel: |
 |
|
| Theoran hat Folgendes geschrieben: | | Jetzt ist mir aber nicht ganz klar, wie ich an dieser Stelle weitermachen muss. |
Laut Aufgabenstellung sollst Du i(t) grafisch darstellen, also die Funktion i(t) zeichnen.
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 11. Apr 2019 14:24 Titel: Theoran Verfasst am: 11. Apr 2019 14:24 Titel: |
 |
|
Das ist ja schon einen Schritt weiter. Aber meine Lösung entspricht ja noch nicht der Musterlösung.
PS: Ich nehme an, hier kommt die Scheitelpunktform ins Spiel, die Du schon angeschnitten hast.
|
|
 |
Steffen Bühler
Moderator
Anmeldungsdatum: 13.01.2012
Beiträge: 7246
|
 Steffen Bühler Verfasst am: 11. Apr 2019 17:02 Titel: Steffen Bühler Verfasst am: 11. Apr 2019 17:02 Titel: |
 |
|
Deine Lösung und die Musterlösung sind identisch. Wie gesagt, multipliziere die Musterlösung aus, dann siehst Du es.
Und wie man umgekehrt von Deiner Lösung auf die Scheitelpunktform kommt, verrät Dir z.B. Wiki.
Viele Grüße
Steffen
|
|
 |
Theoran
Anmeldungsdatum: 25.03.2019
Beiträge: 24
|
 Theoran Verfasst am: 20. Apr 2019 12:26 Titel: Theoran Verfasst am: 20. Apr 2019 12:26 Titel: |
 |
|
Auch wenn es schon ein paar Tage her ist, muss ich das Thema nochmal aufmachen - schon um mich nochmal für die ganzen Antworten zu bedanken.
GvC hatte in einer Seiner ersten Antworten geschrieben:
| Zitat: | | Da der Scheitelpunkt der Parabel aber bekannt ist, lässt sich die Scheitelform der Parabelgleichung sofort hinschreiben, in der nur noch der Koeffizient a als Unbekannte auftaucht, die sich dann aus der Gleichung für Q(4s) leicht bestimmen lässt. |
Ich habe aus meinem errechneten Ergebnis die Scheitelform gebildet (dank Deiner Wiki-Verlinkung).
Wenn ich GvC richtig verstehe, gibt es aber die Möglichkeit, diese Form auch ohne das Aufstellen der drei Gleichungen zu erreichen, richtig?
|
|
 |
|

















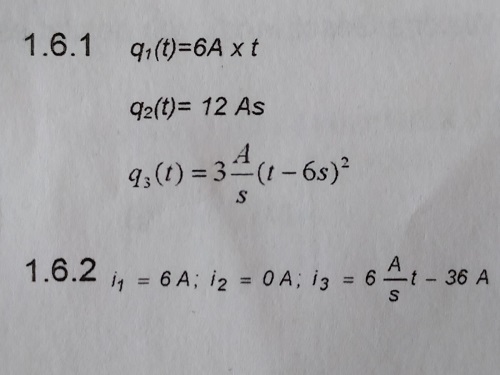
 Abschnitt: Zwischen 0 und 2 s nimmt die Ladungsmenge gleichmäßig von 0 bis zum Wert von 12 As zu.
Abschnitt: Zwischen 0 und 2 s nimmt die Ladungsmenge gleichmäßig von 0 bis zum Wert von 12 As zu.
 )
)