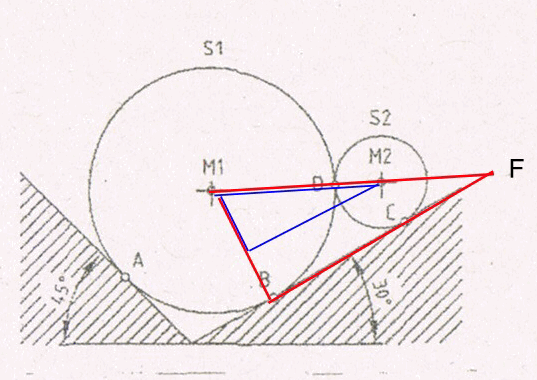
| Zentrales Kräftesystem: zwei Scheiben in einer Rinne |
| Autor | Nachricht | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| rob1234 Anmeldungsdatum: 30.04.2017 Beiträge: 20 |
|
|||||||||||||||||
| Myon Anmeldungsdatum: 04.12.2013 Beiträge: 5870 |
|
|||||||||||||||||
| rob1234 Anmeldungsdatum: 30.04.2017 Beiträge: 20 |
|
|||||||||||||||||
| Myon Anmeldungsdatum: 04.12.2013 Beiträge: 5870 |
|
|||||||||||||||||
| rob1234 Anmeldungsdatum: 30.04.2017 Beiträge: 20 |
|
|||||||||||||||||
| Myon Anmeldungsdatum: 04.12.2013 Beiträge: 5870 |
|
|||||||||||||||||
| rob1234 Anmeldungsdatum: 30.04.2017 Beiträge: 20 |
|
|||||||||||||||||
| Verwandte Themen - die Neuesten | |||||
| Themen | Antworten | Autor | Aufrufe | Letzter Beitrag | |
|---|---|---|---|---|---|
 |
Elektrisches Feld von zwei Punktladungen | 3 | sternenwarte | 962 | 19. März 2024 12:20 sternenwarte |
 |
Zusammenstoß von drei Scheiben | 1 | Gasttt | 714 | 03. März 2024 10:31 Myon |
 |
Zeitentwicklung bei zwei unterscheidbaren Teilchen in 1D | 1 | justlikemanuel | 1163 | 31. Jan 2024 11:17 TomS |
 |
Gesamtspin zwei ununterscheidbarer Teilchen | 1 | Sirius02 | 1749 | 21. Jan 2024 16:06 TomS |
 |
Mischtemperatur von zwei Gasen | 0 | Thomas2001 | 882 | 19. Jan 2024 18:26 Thomas2001 |
| Verwandte Themen - die Größten | |||||
| Themen | Antworten | Autor | Aufrufe | Letzter Beitrag | |
|---|---|---|---|---|---|
 |
Schwarze Löcher = Schwarze Scheiben? | 218 | TomW | 32125 | 01. Jun 2014 08:06 TomW |
 |
Wie "kommunizieren" zwei Dauermagnete elektromag.? | 192 | Vice Versa | 8291 | 17. Jul 2022 09:28 TomS |
 |
Zwei entgegengesetzte Laserpointer | 87 | Gast | 18493 | 17. Sep 2023 06:43 TomS |
 |
Resultierende aus zwei Kraeften und Winkel | 59 | Saetjs | 6492 | 03. Jun 2021 10:22 roycy |
 |
Zwei Federn und ein Massestück | 44 | Mathology | 11183 | 25. Apr 2017 21:50 Mathology |
| Verwandte Themen - die Beliebtesten | |||||
| Themen | Antworten | Autor | Aufrufe | Letzter Beitrag | |
|---|---|---|---|---|---|
 |
Reihenschaltung zwei Glühbirnen | 5 | falloutboy94 | 49760 | 09. Jan 2006 21:58 Gast 12 |
 |
Zwei Massen über Rolle verbunden! | 5 | Tremonia | 46681 | 24. Mai 2012 11:36 Tremonia |
 |
Schweben einer Ladung zwischen zwei Kondensatorplatten | 15 | chell | 45949 | 13. Mai 2013 12:10 Thomas-07 |
 |
Schwarze Löcher = Schwarze Scheiben? | 218 | TomW | 32125 | 01. Jun 2014 08:06 TomW |
 |
Finden des Magnets bei zwei Metallstäben | 7 | Céleste | 31096 | 22. Jul 2022 12:20 Ayane89 |