| Autor |
Nachricht |
Mia22
Anmeldungsdatum: 18.10.2017
Beiträge: 1
|
 Mia22 Verfasst am: 18. Okt 2017 15:57 Titel: Pool Erwärmung durch Sonne |
 |
|
Meine Frage:
Ich möchte wissen ob sich bei gleicher Voraussetzung reiner Sonneneinstrahlung ein grosser Pool, z.b. 10x20x3mTiefe und ein kleiner Pool, z.b. 2x3x 3m Tiefe gleich schnell aufheizen oder der gr. Pool (um eieviel) länger braucht.Formel und Begründung wäre klasse. Danke!
Meine Ideen:
Meiner Meinung nach ist der kleine schneller warm bzw nach gleich langer Sonneneinstrahlung wärmer als der grosse Pool.
Meine Begründung:
Weniger Liter zu erwärmen, und pool Wände Wärmeabgabe.
meine Freundin meint gleich schnell aufgeheizt - gleiche Zemperatur im gr. Und kl. Becken weil gl. Tiefe und Sonneneinstrahlung auf m2 maßgeblich. |
|
 |
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 18. Okt 2017 17:06 Titel: |
|
|
|
Die Wärmezufuhr pro Volumen ist bei beiden Pools gleich groß. Insofern hätte Deine Freundin recht. Allerdings sind die Wandflächen im großen Pool und damit die Wärmeabgabe an das umgebende Erdreich größer. Insofern hättest Du recht, allerdings nur mit dem zweiten Teil Deiner Begründung. |
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 20. Okt 2017 07:46 Titel: |
|
|
| Zitat: | | Allerdings sind die Wandflächen im großen Pool und damit die Wärmeabgabe an das umgebende Erdreich größer. Insofern hättest Du recht, allerdings nur mit dem zweiten Teil Deiner Begründung. |
Das sehe ich anders.
Im großen Pool ist die Wandfläche bezogen auf das Volumen (und auch bezogen auf die Einstrahlfläche) kleiner und entsprechend ändert sich auch die Wärmeabgabe. Insofern wäre der größere Pool (gleicher Tiefe) sogar schneller warm.
. |
|
|
Duke711
Anmeldungsdatum: 26.01.2017
Beiträge: 434
|
| Duke711 Verfasst am: 20. Okt 2017 18:07 Titel: |
|
|
Die Frage ist nicht ausreichend definiert.
Wenn die beiden Pools die gleiche Sonneinstrahlungsfläche haben. Nur aber eine unterschiedliche Tiefe, dann ist der kleine Pool deutlich schneller erwärmt.
Denn die meiste Wärme wird durch die Sonne, mit z.B. 1300 W/m² übertragen.
Wären es vom Erdreich/Wände gerade mal 1 - 5 W/m² sind.
Wenn beide Pools nun sich von ihrer Größe nur über die Sonneneinstrahlungsfläche unterscheiden (gleiche Tiefe). Dann erwärmen sich beide gleich schnell.
Denn doppelte Wassermasse = doppelte Sonneneinstrahlungsfläche = doppelt zugeführte Wärme.
Die 1 - 5 W/m² fallen kaum ins Gewicht, so dass man diese vernachlässigen kann.
Die Aussage Frankx ist defintiv falsch. |
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 20. Okt 2017 20:54 Titel: |
|
|
| Zitat: | | Die Aussage Frankx ist defintiv falsch. |
Bevor man hier Vokabeln wie "definitiv" verwendet sollte man definitiv die Fragestellung und die bisherigen Antworten sorgfältig lesen, sonst macht man sich definitiv lächerlich.
1. Es war stets nur von Pools gleicher Tiefe die Rede.
2. Schon in der Fragestellung war vom Einfluss der Wände die Rede.
3. Meine Aussage war rein qualitativ (schneller, langsamer)
4. Ob das in der Praxis vernachlässigbar ist, hängt von vielen Parametern ab.
GVC ist ein kleiner Lapsus unterlaufen, das kann mal passieren.
Ich hatte eigentlich gehofft, dass GVC das selbst bestätigt.
. |
|
|
Duke711
Anmeldungsdatum: 26.01.2017
Beiträge: 434
|
| Duke711 Verfasst am: 20. Okt 2017 21:13 Titel: |
|
|
| Frankx hat Folgendes geschrieben: |
Insofern wäre der größere Pool (gleicher Tiefe) sogar schneller warm. |
= Definitiv falsch. |
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 20. Okt 2017 22:06 Titel: |
|
|
| Zitat: | | = Definitiv falsch. |
Wir sind hier im Physikforum. Da wäre eine physikalische Begründung deiner Behauptung angebracht.
Wenn es dir schwer fällt, meinen obigen Ausführungen zu folgen, darfst du auch nachfragen.
Ansonsten hat dein Beitrag ungefähr den Wert der aktuell weltweit beliebten alternativen Fakten.
. |
|
|
Duke711
Anmeldungsdatum: 26.01.2017
Beiträge: 434
|
| Duke711 Verfasst am: 20. Okt 2017 23:54 Titel: |
|
|
Wurde bereits begründet, aber Deine Ausreden werden immer lächerlicher und mir ist das nun auch viel zu unseriös. Mal davon abgesehen, dass Du diese Falschaussage überhaupt nicht begründet hast, sondern nur eine Behauptung getroffen wurde.
Such Dir für deine unreifen Spielchen einen anderen Kandidaten. |
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 21. Okt 2017 08:08 Titel: |
|
|
| Zitat: | | dass Du diese Falschaussage überhaupt nicht begründet hast |
In der Hoffnung, dass deine Rechenleistung die Leseleistung wesentlich übertrifft, werte ich das mal wohlwollend als Nachfrage und rechne dir das an Hand der eingangs gegebenen Werte vor.
großer Pool:
Volumen 10x20x3m Tiefe=600m³
Einstrahlfläche 10x20=200m²
Wandfläche 2x(10+20)*3=180m²
Verhältnis Einstrahlfläche zu Volumen
200/600 = 1/3 = ca. 0,33 m²/m³
Verhältnis Wandfläche zu Volumen
180/600=0,3 m²/m³
kleiner Pool:
Volumen 2x3x3m Tiefe=18m³
Einstrahlfläche 2x3=6m²
Wandfläche 2x(2+3)*3=30m²
Verhältnis Einstrahlfläche zu Volumen
6/18=1/3 = ca. 0,33 m²/m³
Verhältnis Wandfläche zu Volumen
30/18=ca. 1,67 m²/m³
Man sieht:
1. Dass für jeden Kubikmeter Wasser in beiden Pools die gleiche Einstrahlfläche (ca. 0,33 m²/m³) zur Verfügung steht, d.h. jeder Kubikmeter die gleiche Heizleistung erhält
2. Dass im großen Pool für jeden Kubikmeter Wasser eine geringere Wandfläche zur Wärmeabgabe (0,3 m²/m³), als im kleinen Pool (ca. 1,67 m²/m³) zur Verfügung steht.
Das bedeutet, bei ansonsten gleichen Bedingungen, dass das Wasser im kleinen Pool je Kubikmeter mehr Wärme abgeben kann und somit insgesamt langsamer erwärmt wird.
Ob das in der Praxis relevant ist, hängt von mehreren Randbedingungen (Absorptionsgrad, Wärmedurchgangswerte, Ausgangstemperaturen,...) ab, vermutlich sind die Differenzen eher gering. Hier geht es aber erst mal um eine physikalisch begründete qualitative Aussage.
| Zitat: | | und mir ist das nun auch viel zu unseriös. |
Der Punkt geht definitiv an dich.
.
Zuletzt bearbeitet von Frankx am 21. Okt 2017 08:46, insgesamt einmal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 21. Okt 2017 08:36 Titel: |
|
|
Ich würde mal eine vollständige Bilanzgleichung aufstellen.
Dazu benötigt man zunächst wie Wärmeleitung. Diese gilt für alle Oberflächen, d.h. zum einen gibt der Pool Wärme an das Erdreich ab oder nimmt Wärme auf (wohl eher untypisch) zum anderen nimmt er ggf. Wärme aus der Luft auf oder gibt sie ab (früh morgens ist das Wasser vom Vortag noch wärmer als die Luft)
Dann benötigt man die Aufnahme der Wärme über die Sonneneinstrahlung sowie die Abgabe der Wärme über die Strahlung eines schwarzen Körpers. Letztere ist ggü. dem Wärmetransport mittels Wärmeleitung meist zu vernachlässigen; man sollte jedoch mal alle Größen abgeschätzt haben, um beurteilen zu können, ob die Aufgabe überhaupt sinnvoll gestellt ist.
Ohne Wissen über die Temperaturen von Erdreich, Luft und Wasser kann man m.E. keine vernünftige Aussage treffen.
https://de.m.wikipedia.org/wiki/Wärmeleitfähigkeit |
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 21. Okt 2017 08:45 Titel: |
|
|
| Zitat: | | Ohne Wissen über die Temperaturen von Erdreich, Luft und Wasser kann man m.E. keine vernünftige Aussage treffen. |
Sicher nicht quantitativ, aber qualitativ schon, da all deine angeführten Einflüsse für beide Pools als identisch vorausgesetzt werden.
. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 21. Okt 2017 08:49 Titel: |
|
|
| Frankx hat Folgendes geschrieben: | | Zitat: | | Ohne Wissen über die Temperaturen von Erdreich, Luft und Wasser kann man m.E. keine vernünftige Aussage treffen. |
Sicher nicht quantitativ, aber qualitativ schon, da all deine angeführten Einflüsse für beide Pools als identisch vorausgesetzt werden. |
Nur zu Beginn, später nicht.
Wenn sich die Pools erwärmen, das umgebende Erdreich jedoch konstante Temperatur hat (vernünftige Näherung) dann bleiben die Einflüsse nur identisch, wenn du identische Erwärmung voraussetzt. Das dürfen wir aber nicht voraussetzen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 21. Okt 2017 09:38 Titel: |
|
|
| Zitat: | | Wenn sich die Pools erwärmen, das umgebende Erdreich jedoch konstante Temperatur hat (vernünftige Näherung) dann bleiben die Einflüsse nur identisch, wenn du identische Erwärmung voraussetzt. Das dürfen wir aber nicht voraussetzen. |
Du beschreibst wieder Quantitäten. Sofern aber überhaupt über die Wände Wärme abgegeben wird, ist das Ergebnis qualitativ das gleiche. Der größere Pool erwärmt sich schneller.
Stell dir zwei völlig identische quadratische Pools vor.
Für beide gelten die gleichen Randbedingungen und demzufolge erwärmen sie sich auch identisch.
Jetzt rücken wir die Pools zusammen, bis sie sich an jeweils einer Wand berühren. Dann entfernen wir die gemeinsame Wand.
Was hat sich im Vergleich zur Ausgangssituation geändert?
Dem jetzt größeren Pool fehlt nun im Vergleich zur Summe der beiden kleinen Pools eine Wandfläche zur Wärmeabgabe.
Also wird er schneller warm, als die beiden jeweiligen einzelnen kleinen Pools.
Unter Kenntnis der anderen Randbedingungen könnte man das mittels Software sicher simulieren und dann auch quantitative Aussagen treffen.
. |
|
|
Duke711
Anmeldungsdatum: 26.01.2017
Beiträge: 434
|
| Duke711 Verfasst am: 21. Okt 2017 13:43 Titel: |
|
|
| Frankx hat Folgendes geschrieben: | Man sieht:
1. Dass für jeden Kubikmeter Wasser in beiden Pools die gleiche Einstrahlfläche (ca. 0,33 m²/m³) zur Verfügung steht, d.h. jeder Kubikmeter die gleiche Heizleistung erhält
2. Dass im großen Pool für jeden Kubikmeter Wasser eine geringere Wandfläche zur Wärmeabgabe (0,3 m²/m³), als im kleinen Pool (ca. 1,67 m²/m³) zur Verfügung steht. |
Deine Leseleistung lässt ebenfalls zu wünschen übrig:
| Duke711 hat Folgendes geschrieben: |
Denn die meiste Wärme wird durch die Sonne, mit z.B. 1300 W/m² übertragen. Wären es vom Erdreich/Wände gerade mal 1 - 5 W/m² sind. |
Du hast überhaupt nicht aufgepasst.
Jetzt rechne am besten nochmal und richtig über die spezifische Wärmekapazität, überschlägige Wärmedurchgangskoeffizienten, anstatt über ein einfaches Volumen/Oberflächenverhältnis.
Dann können wir gerne weiter diskutieren, ansonsten ist die Diskussion hier mit endgültig beendet.
Im übrigen kannst Du dir auch diese Rechnerrei sparen.
Denn wenn man den Pool nun bei gleich bleibender Tiefe verdoppelt. Dann verdoppeln sich die Oberflächen und somit der Wärmeeintrag. Da sich ebenfalls die Wassermasse verdoppelt, bleibt die zugeführte Wärmestromdichte im Verhältnis zur Wassermasse gleich und deshalb erwärmt sich der doppelt so große Pool bzw. größere Pool nicht schneller.
Man könnte genauso auch ein sehr kleines, finites Element, vom Pool betrachten. Da es sich in Richtung Längs/Querachse um eine physikalische Symmetrie handelt. Ob ich nun einen Streifen oder den gesamten Pool betrachte, macht bei einen stationären Fall überhaupt keinen Unterschied. |
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 21. Okt 2017 14:13 Titel: |
|
|
| Zitat: | Duke711 hat Folgendes geschrieben:
| Zitat: | | Denn die meiste Wärme wird durch die Sonne, mit z.B. 1300 W/m² übertragen. Wären es vom Erdreich/Wände gerade mal 1 - 5 W/m² sind. |
|
Oha, 1300 Watt/m² ?
Das wäre dann ein Pool auf dem Mond, aber egal.
| Zitat: | | Jetzt rechne am besten nochmal und richtig über die spezifische Wärmekapazität, überschlägige Wärmedurchgangskoeffizienten, |
Such dir eine Wärmekapazität und eine beliebigen Wärmeübergangskoeffizienten aus. Am prinzipiellen Ergebnis (großer Pool wird schneller warm) ändert das nichts.
| Zitat: | | Denn wenn man den Pool nun bei gleich bleibender Tiefe verdoppelt. Dann verdoppeln sich die Oberflächen und somit der Wärmeeintrag. Da sich ebenfalls die Wassermasse verdoppelt, bleibt die zugeführte Wärmestromdichte im Verhältnis zur Wassermasse gleich |
Das habe ich nicht bezweifelt, sondern oben sogar rechnerisch dargestellt.
| Zitat: | | und deshalb erwärmt sich der doppelt so große Pool bzw. größere Pool nicht schneller. |
Nur unter der Voraussetzung, dass der Einfluss der Wände völlig unberücksichtigt bleibt, weil sich die Wandfläche eben nicht genau so verdoppelt. Aber gerade nach dem Einfluss der Größe der Wandfläche wurde ja in der Aufgabenstellung gefragt.
| Zitat: | | Man könnte genauso auch ein sehr kleines, finites Element, vom Pool betrachten. |
Oh, jetzt kommt man noch mit "finiten Elementen". Das klingt gleich so wissenschaftlich. Da muss ich nun wirklich passen.
. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 22. Okt 2017 11:00 Titel: Re: Pool Erwärmung durch Sonne |
|
|
| Mia22 hat Folgendes geschrieben: | | Formel und Begründung wäre klasse. |
Die zugeführte Wärme durch die Sonne ergibt sich aus dem Wärmestrom
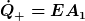
wobei E für die Solarkonstante, d.h. die Strahlungsleistung pro Fläche, und A_1 für die Oberfläche des Pools steht.
Die mit der Umgebung ausgetauschte Wärme ergibt sich aus dem Wärmestrom
)
Hier stehen A_a für die Flächen, lambda_a für deren Wärmeleitung und T_a für die jenseits der Fläche geltende Temperatur. Im Folgenden setzen wie a=1 für die Grenzfläche zur Luft bzw. a=2 zum Erdreich.
Der gesamte Wärmestrom ist die Summe
)
Aus dem Wärmestrom ergibt sich die Temperaturänderung zu
Dabei steht c für die spezifischen Wärmekapazität des Wassers und M für dessen Masse; letztere ist direkt proportional zum Volumen V.
Einsetzen liefert:
)
Wir setzen einen quadratischen Pool mit Länge L und Tiefe h; für die Flächen A_1 und A_2 sowie für das Volumen V gilt dann
Einsetzen liefert
 - \lambda_2(L^2 + 4Lh)(T-T_2))
 - \lambda_2(1+x)(T-T_2))
mit x = 4h/L
Nun kann man diverse Überlegungen anstellen.
Setzt man die Temperaturänderung links gleich Null, so kann man durch Auflösen nach T die Gleichgewichtstemperatur bererechnen.
Vernachlässigt man den Wärmeaustausch mit Erdreich und Luft, so folgt
d.h. die Temperatur ist unabhängig von L und damit von der Fläche, jedoch abhängig von h (was laut erstem Beitrag in beiden Fällen identisch ist).
Unter dieser Voraussetzung erwärmen sich beide Pools gleich schnell.
Der Wärmeaustausch mit der Umgebung wird wichtig, wenn die Strahlungsleistung sinkt (im Winter) oder wenn die Temperaturdifferenzen rechts hoch sind (im Winter, extrem kaltes Wasser bei extrem hoher Lufttemperatur, noch vom Tag warmes Wasser in einer kühlen Nacht, wenn die Wassertemperatur weit von der Gleichgewichtstemperatur entfernt ist).
In all diesen Fällen kann man zunächst keine genauere Angabe machen, ohne zunächst die relevanten Größen besser zu kennen. Der einzige und damit relevante Term mit L-Abhängigkeit ist dabei rechts
)
Dieser Term wird insbs. wichtig für großes x also tiefe Pools bei identischer Fläche.
Generelle Anmerkung: ich habe optimale Durchmischung des Wassers angenommen d.h. Temperaturunterschiede vernachlässigt; Erdreich und Luft sollen jeweils Konstante Temperatur haben. Außerdem habe ich Wärmeaustausch mit der Luft über Konvektion (insbs. Wind) vernachlässigt. |
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 22. Okt 2017 14:48 Titel: |
|
|
Hallo TomS,
Respekt für deine gründliche Herleitung.
Aber warum beantwortest du nicht erst mal einfach die gestellte Frage.
| Zitat: | | gleicher Voraussetzung reiner Sonneneinstrahlung ein grosser Pool, z.b. 10x20x3mTiefe und ein kleiner Pool, z.b. 2x3x 3m Tiefe gleich schnell aufheizen oder der gr. Pool (um eieviel) länger braucht. |
Der Fragesteller wollte keinen Tag-Nacht-Rhythmus, keinen Sommer-Winter-Einfluss, keine Schwarzkörperstrahlung, keine Gezeiten, kein etc.
| Zitat: | Meiner Meinung nach ist der kleine schneller warm bzw nach gleich langer Sonneneinstrahlung wärmer als der grosse Pool.
Meine Begründung:
Weniger Liter zu erwärmen, und [b]pool Wände Wärmeabgabe[/b] |
Dass es bei Vernachlässigung des Einflusses der Wände, aber sonst gleichen Bedingungen, keinen Unterschied gibt, ist doch unbestritten.
Es wurde aber auch explizit nach dem Einfluss der Wände gefragt.
Bei letzterem gab es verschiedene Meinungen:
Es geht erst mal nur um die qualitative Aussage.
GVC sagte, kleiner Pool wird schneller warm.
Ich sage, großer Pool wird schneller warm.
Beide haben wir unsere Meinung begründet.
Die Aufgabe ist doch nicht so schwer, vom Schwierigkeitsgrad und Typ her passt das locker in die Oberstufe oder Gymnasium.
Wo ist nun für dich als Physiker das Problem, bei einem von uns beiden den Fehler in der Argumentation aufzuzeigen?
Hier geht es um Physik, nicht um persönliche Befindlichkeiten.
. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 22. Okt 2017 15:15 Titel: |
|
|
| Frankx hat Folgendes geschrieben: | Hallo TomS,
Respekt für deine gründliche Herleitung. |
Danke
| Frankx hat Folgendes geschrieben: | | Aber warum beantwortest du nicht erst mal einfach die gestellte Frage. |
Weil sie nicht so einfach zu beantworten ist.
| Frankx hat Folgendes geschrieben: | | Die Aufgabe ist doch nicht so schwer, vom Schwierigkeitsgrad und Typ her passt das locker in die Oberstufe oder Gymnasium. |
Mit allen Feinheiten?
| Frankx hat Folgendes geschrieben: | | Wo ist nun für dich als Physiker das Problem, bei einem von uns beiden den Fehler in der Argumentation aufzuzeigen? |
Ich bevorzuge ein anderes Vorgehen: ich präsentiere eine Herleitung, die ihr nachvollziehen und dabei kritisch prüfen könnt; evtl. hab' ich einen Fehler gemacht.
Ausgehend von den beiden Pools mit zunächst identischer Temperatur folgt der Unterschied der Temperaturentwicklung aus dem letzten Term
)
Ich habe den Term mit negativem Vorzeichen notiert, d.h. als Energieabgabe. Das trifft dann zu, wenn die Wassertemperatur T größer ist als die Temperatur des umgeben Erdreichs. Dann wirkt dieser Term mit x = 4h/L bei größerer Abmessung L der Erwärmung geringer entgegen. Der größere Pool erwärmt sich schneller.
Ist die Wassertemperatur T dagegen noch kleiner als die Temperatur des umgeben Erdreichs, dann liegt Energieaufnahme vor. Dabei unterstützt dieser Term mit x = 4h/L bei größerer Abmessung L diese Erwärmung weniger stark. Der kleinere Pool erwärmt sich schneller.
Bitte prüft das nochmal kritisch.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
| TomS Verfasst am: 22. Okt 2017 17:43 Titel: Re: Pool Erwärmung durch Sonne |
|
|
Um das noch besser zu verstehen, kann man für die folgende DGL
zunächst als Näherung ansetzen, dass der Wärmeaustausch mit der Luft gering ist, d.h. dass der Term in a=1 verschwindet.
Dann führt man die neue Variable tau mittels
 = T_2(\tau - 1))
ein; diese steht für die Abweichung der Wassertemperatur von der des Erdreichs. Man löst die resultierende Differentialgleichung in tau
T_2\tau)
mittels Variation der Konstanten.
Anschließend vergleicht man für identische Anfangsbedingung den Verlauf der Lösung für unterschiedliche Werte von x = 4h/L. |
|
|
Frankx
Anmeldungsdatum: 04.03.2015
Beiträge: 982
|
| Frankx Verfasst am: 22. Okt 2017 19:10 Titel: |
|
|
| Zitat: | | Bitte prüft das nochmal kritisch. |
Ich konnte keinen Fehler finden.
| Zitat: | | Das trifft dann zu, wenn die Wassertemperatur T größer ist als die Temperatur des umgeben Erdreichs. Dann wirkt dieser Term mit x = 4h/L bei größerer Abmessung L der Erwärmung geringer entgegen. Der größere Pool erwärmt sich schneller. |
Das wollte ich so hören.
Dass die Wassertemperatur nicht unter der des Erdreiches liegt (auch anfangs nicht) kann imho aus der Formulierung "gleicher Voraussetzung reiner Sonneneinstrahlung" und "pool Wände Wärmeabgabe" in der Aufgabenstellung geschlossen werden.
D.h. Erwärmeeintrag ausschließlich durch Sonne, Wärmeabgabe über die Wände.
Ich denke auch GVC hatte das so betrachtet, weshalb ich bei ihrer Schlussfolgerung von einem Lapsus sprach.
| Zitat: | | Ist die Wassertemperatur T dagegen noch kleiner als die Temperatur des umgeben Erdreichs, dann liegt Energieaufnahme vor. Dabei unterstützt dieser Term mit x = 4h/L bei größerer Abmessung L diese Erwärmung weniger stark. Der kleinere Pool erwärmt sich schneller. |
Unter diesen Voraussetzungen stimme ich dir zu.
War doch gar nicht so schwer.
Ich denke, damit kann nun auch Duke177 definitiv zufrieden gestellt werden. ;-)
. |
|
|
|
Registrieren
Login
FAQ
Suchen
