| Autor |
Nachricht |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
|
 |
Auwi
Anmeldungsdatum: 20.08.2014
Beiträge: 602
|
 Auwi Verfasst am: 28. Okt 2016 16:40 Titel: Auwi Verfasst am: 28. Okt 2016 16:40 Titel: |
 |
|
|
Vielleich ist das logarithmische Dekretment die passende Größe...
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 28. Okt 2016 17:00 Titel: Random Verfasst am: 28. Okt 2016 17:00 Titel: |
 |
|
Danke, stimmt.
Die Aufgabe ist nämlich:
1. Bestimmen Sie die Dämpfungskonstante  aus der zeitlichen Abnahme der Amplitudenmaxima. aus der zeitlichen Abnahme der Amplitudenmaxima.
2. Zeichnen Sie die Amplitudenwerte in ein einfach-logarithmischens Papier und bestimmen Sie die Dämpfungskonstante  aus der Steigung der Geraden. aus der Steigung der Geraden.
Aufgabe2 wäre ja, was du erwähnt hast. Aber wie geht Aufgabe1?
So wie ich es erläutert habe?
|
|
 |
Auwi
Anmeldungsdatum: 20.08.2014
Beiträge: 602
|
 Auwi Verfasst am: 28. Okt 2016 20:24 Titel: Auwi Verfasst am: 28. Okt 2016 20:24 Titel: |
 |
|
Ich meine:
\over Amplitude(n)}])\,/\,T)
Das ganze kann man sicher auch logarithmisch über viele Amplituden "mitteln", das dürfte dann die "Steigung" dieser Funktion sein.
Auch die Kreisfrequenz der gedämpften Schwingung hängt von "delta" ab.
Meines Wissens gilt für sie:

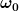 = Kreisfrequenz der ungedämpften Schwingung = Kreisfrequenz der ungedämpften Schwingung
(Fehler in der ersten Formel beseitigt, vergessen, durch T zu dividieren)
Zuletzt bearbeitet von Auwi am 04. Nov 2016 13:46, insgesamt 2-mal bearbeitet |
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 28. Okt 2016 20:52 Titel: Re: Dämpfungskonstante und -koeffizient bestimmen franz Verfasst am: 28. Okt 2016 20:52 Titel: Re: Dämpfungskonstante und -koeffizient bestimmen |
 |
|
| Random hat Folgendes geschrieben: | 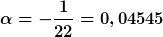 |

|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 28. Okt 2016 23:08 Titel: Random Verfasst am: 28. Okt 2016 23:08 Titel: |
 |
|
Verstehe, danke.
1. Okay, d.h wenn ich die Amplituden einfach logarithmisch darstelle auf der y-Achse, dann ergibt die Steigung meine Dämpfungskonstante?
2. Ist aber jetzt -1/22=-0,0454545 auch meine Dämpfungskonstante? (Ja sry, ich habe das - vergessen, oder was meintest du @franz?)
|
|
 |
thx2
Gast
|
 thx2 Verfasst am: 28. Okt 2016 23:33 Titel: thx2 Verfasst am: 28. Okt 2016 23:33 Titel: |
 |
|
Die Aufgabe ist etwas irreführend
Die Scheibe wurde um 100mm ausgelenkt
und dann der Startpunkt auf Null gesetzt
Diese 100mm muss man aber bei der Berechnung wieder abziehen
Aus dem 1.Bild nimmt man 2 Punkte
und dann wie üblich
 })
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 29. Okt 2016 08:20 Titel: Random Verfasst am: 29. Okt 2016 08:20 Titel: |
 |
|
Hmm ok danke.
Aber wir sehen ja im 2. Teil die gedämpfte Schwingung und ich hab mir die Peaks, also Hochpunkte, rausgesucht und diese verbunden. Das Programm hat mir dann die oben geschriebene Exponentialfunktion ausgegeben.
Dann müsste doch die "Steigung" der EXP-Fkt. -1/22 sein, oder nicht? Also wie k die Steigung von e^kx wäre. Und -1/22 wäre dann mein Dämpfungskoeffizient.
Funktioniert das so?
|
|
 |
thx2
Gast
|
 thx2 Verfasst am: 29. Okt 2016 09:26 Titel: Re: Dämpfungskonstante und -koeffizient bestimmen thx2 Verfasst am: 29. Okt 2016 09:26 Titel: Re: Dämpfungskonstante und -koeffizient bestimmen |
 |
|
| Random hat Folgendes geschrieben: |
Aber wir sehen ja im 2. Teil die gedämpfte Schwingung und ich hab mir die Peaks, also Hochpunkte, rausgesucht und diese verbunden. Das Programm hat mir dann die oben geschriebene Exponentialfunktion ausgegeben.
Die Exp-Funktion lautet: =391.64911*e^{-x/22.11516}-90.56674)
|
gesucht wird eine Grenzkurve der Form
 })
dazu muss man von den gegebenen Werten 100mm abziehen
wenn du die 100mm nicht abziehst müsste so etwas
 }+100mm)
herauskommen
Aber keine -90.6mm
Vielleicht hat man in der Aufgabe nur eine sehr ungenaue Exponentialfunktion
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 29. Okt 2016 11:28 Titel: Random Verfasst am: 29. Okt 2016 11:28 Titel: |
 |
|
Ja aber wie man sieht, liegt doch die Exponentialfunktion genau an?
Oder sollte diese Exponentialfunktion genau bei y=100mm ausklingen?
Denn wie es aussieht klingt diese bei Null aus.
|
|
 |
thx2
Gast
|
 thx2 Verfasst am: 29. Okt 2016 13:05 Titel: thx2 Verfasst am: 29. Okt 2016 13:05 Titel: |
 |
|
| Random hat Folgendes geschrieben: | Ja aber wie man sieht, liegt doch die Exponentialfunktion genau an?
|
Ich war bisher aufgrund dieser Formel
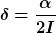
der Meinung,dass hier folgende Dämpfung vorliegt (Wirbelstrom?)

Ist das so?
Wenn ja kann man nicht irgend eine Exponentialfunktion nehmen
sondern nur die,die ich hingeschrieben habe
| Random hat Folgendes geschrieben: |
Oder sollte diese Exponentialfunktion genau bei y=100mm ausklingen?
|
Wenn es sich um die Standardaufgabe handelt
Ja
| Random hat Folgendes geschrieben: |
Denn wie es aussieht klingt diese bei Null aus. |
diese
=391.64911*e^{-x/22.11516}-90.56674)
klingt bei -90.6 aus
Am besten nochmal die ganze Aufgabe hinschreiben
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
|
 |
thx2
Gast
|
 thx2 Verfasst am: 29. Okt 2016 17:40 Titel: thx2 Verfasst am: 29. Okt 2016 17:40 Titel: |
 |
|
 })
1 und 2 bedeutet nicht,dass die beiden Hochpunkte nebeneinanderliegen müssen
Im Gegenteil
Sie sollte weit auseinanderliegen
(aber nicht zu weit nach rechts gehen wegen der Ungenauigkeit)
Ich habe zB
1s 184mm und
11.5s 45mm
ich habe die 100mm abgezogen (ist besser)
 )

|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
|
 |
thx2
Gast
|
 thx2 Verfasst am: 29. Okt 2016 19:44 Titel: thx2 Verfasst am: 29. Okt 2016 19:44 Titel: |
 |
|
 })
wenn tx=t1 dann ist Ax=A1
also
 })
da kann man jetzt die 100mm dazuaddieren
 }+100mm)
es ist aber so,dass man die Funktion
 }+100mm)
bisher nur mit einfachen Mitteln gesucht hat und deshalb darf man
keine allzugroße Genauigkeit erwarten
die gibt es aber meistens sowieso nicht
|
|
 |
Random
Anmeldungsdatum: 25.01.2016
Beiträge: 42
|
 Random Verfasst am: 29. Okt 2016 21:50 Titel: Random Verfasst am: 29. Okt 2016 21:50 Titel: |
 |
|
Hm ja, ist halt ungenau.
Kann man sowas nicht genauer machen?
Oder ist das so, dass mein Schwingungssystem nie 100% Exponentiell abklingen kann, d.h. so eine nach den Amplitudenmaxima abklingende Funktion ist gar ned definiert bzw. gibt es nicht?
Und was ist mit Aufgabe2 gemeint?
|
|
 |
thx2
Gast
|
 thx2 Verfasst am: 30. Okt 2016 10:03 Titel: thx2 Verfasst am: 30. Okt 2016 10:03 Titel: |
 |
|
| Random hat Folgendes geschrieben: |
Kann man sowas nicht genauer machen?
|
Mit linearer Regression
| Random hat Folgendes geschrieben: |
Oder ist das so, dass mein Schwingungssystem nie 100% Exponentiell abklingen kann, d.h. so eine nach den Amplitudenmaxima abklingende Funktion ist gar ned definiert bzw. gibt es nicht?
|
Es gibt noch die Lagerreibung und die Wirbelstrombremse arbeitet sich
auch nicht so exakt
| Random hat Folgendes geschrieben: |
Und was ist mit Aufgabe2 gemeint? |
Amplitudenwerte logarithmieren
|
|
 |
|
















