Dichteoperator eines reinen Zustands

ChancesToTake · Gast

Meine Frage:
Hallo liebe Physik-Freunde,

Wir haben kurz besprochen was reine und gemischte Zustände sind und den Dichteoperator eingeführt. Die Original-Aufgabenstellung meines Problems lautet:

Unter welchen Bedingungen beschreibt

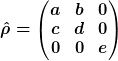
den Dichteoperator eines reinen Zustands?

Meine Ideen:
Um die Koeffizienten zu bestimmen, muss ich natürlich die Bedingungen, die einen reinen Zustand charakterisieren, anwenden. Aus der Vorlesung ist bekannt:

Genutzt habe ich (4)-(6):

Fehlen mir noch irgendwelche Eigenschaften, mit denen ich die Koeffizienten bestimmen kann? Wir haben das Thema Dichteoperatoren nur angerissen und es verwirrt mich ziemlich... Wenn ich die ganzen Gleichungen umstelle, komme ich immer nur auf mehrere mögliche Ergebnisse. Beispielsweise, wenn man auf die Gleichungen aus (5) die PQ-Formel anwendet.

Viele Grüße!

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18007

M.E. hast du keine Gleichung bzw. Bedingung vergessen.

Für Dichtematrizen gilt
- hermitesch
- positiv semidefinit,
- Spur gleich Eins

Für einen reinen Zustand gilt außerdem, dass die Dichtematrix ein Projektor ist.

TomS · Moderator Anmeldungsdatum: 20.03.2009 Beiträge: 18007

Natürlich sind mehrere Lösungen möglich.

Zunächst mal solltest du dir überlegen, was geschieht, wenn die Dichtematrix in einem reinen Zustand und zugleich diagonal ist. Damit hast du sofort b = c = 0. Da die Dichtematrix in einem reinen Zustand ein Projektor sein muss, müssen die Diagonalelemente gleich Eins sein. Und wegen der Spureigenschaft darf nur genau ein Diagonalelement gleich Eins sein, die anderen beiden Null.

Wenn e = 1 gilt, muss m.E. die obere 2*2-Matrix Null sein. Das sollte aber aus deinen Bedingungen folgen.

Wenn e = 0 ist, dann ist die allgemeine Lösung der oberen 2*2-Matrix eine unitäre Transformation der trivialen Projektoren; damit hast du keine eindeutige Lösung.

Anders formuliert: sei der Dichteoperator in einer bestimmten Basis |n> von der Gestalt

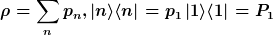
gleich dem Projektor auf den ersten Basisvektor.

Nun ist dein Dichteoperator bzgl. einer anderen Basis |n>' gegeben

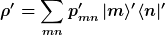
Da die Basen lediglich durch eine unitäre Transformation

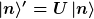
miteinander verknüpft sind, kannst du schreiben

Nun weißt du jedoch, wie der Dichteoperator bzgl. der Basis |n> aussieht und kannst einsetzen

D.h. du erhältst deinen Dichteoperator (in deiner bekannten Basis) durch eine unitäre Transformation dieses Projektors (in der unbekannten Basis). Diese unitäre Transformation ist allgemein gegeben durch eine Vertauschung von Basisvektoren, also z.B. eine Vertauschung von 1 mit 3, sowie zuletzt eine (speziell unitäre) Rotation in den ersten beiden Basisvektoren (e kann ja nur 0 oder 1 sein, und die dritte Zeile und Spalte hat Nichtduagonalelemente = Null).

ChancesToTake · Gast

Vielen Dank für die ganzen hilfreichen Hinweise!
Gerade die Unitäre Transformation habe ich so noch nicht gesehen. Wäre schön, wenn wir in der Uni demnächst mal ein konkretes Beispiel durchrechnen würden.

Viele Grüße und danke nochmal für die schnelle Antwort!