| Autor |
Nachricht |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 17. Sep 2014 10:04 Titel: Dichteoperator - Spurklasse und Messbarkeit TomS Verfasst am: 17. Sep 2014 10:04 Titel: Dichteoperator - Spurklasse und Messbarkeit |
 |
|
Hallo, ich habe ein paar Fragen an die Experten.
Ein Dichteoperator sowie ein Erwartungswert werden i.A. geschrieben als
\,|u\rangle\langle u|)

wobei das System der |u> kein ONS jedoch vollständig sein muss. Dabei sind die Integrale mittels eines geeigneten Maßes zu definieren.
Interessanterweise definiert dies dann ein Wahrscheinlichkeitsmaß, das genau der Bornschen Regel entspricht (s.a. Gleason's Theorem).
Fragen:
wer garantiert, dass die Menge S bzw. das System der |u> selbst messbar ist?
niemand, denn ich weiß ja, dass ich bereits auf der Einheitskugel nicht-messbare Mengen definieren kann!
verletzt ein derartiges rho evtl. die Spurklasse?
liegt der Fehler darin, dass ich kein diskretes System für die |u> verwende? (obwohl das wg. Separabilität immer funktioniert)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
 bassiks Verfasst am: 17. Sep 2014 11:24 Titel: bassiks Verfasst am: 17. Sep 2014 11:24 Titel: |
 |
|
Bevor ich mir darüber Gedanken mache, will ich sicher gehen, dass ich
verstehe, worauf du hinaus willst.
Verstehe ich deine Frage richtig wenn ich sie so formuliere:
Impliziert die Definition eines Dichteoperators die Messbarkeit von S? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 17. Sep 2014 12:40 Titel: TomS Verfasst am: 17. Sep 2014 12:40 Titel: |
 |
|
er andersherum: was bedeutet die Existenz nicht-messbarer Mengen für den Dichteoperator (auf diesen Mengen)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
 bassiks Verfasst am: 17. Sep 2014 13:32 Titel: bassiks Verfasst am: 17. Sep 2014 13:32 Titel: |
 |
|
Auf den ersten Blick denke ich dass die Existenz solcher Mengen nicht wirklich viel für den Dichteoperator bedeutet. Die Messbarkeit der Menge
ist für die Spur erstmal nicht relevant. Die Funktion p(u) muss so gewählt sein, dass die Spur 1 wird. Andernfalls handelt es sich schlicht um keinen Dichteoperator.
Mann könnte jetzt natürlich die Frage nach den notwendigen Eigenschaften von p(u) stellen. Eine sichere Abschätzung wäre vermutlich, dass p(u) einen kompakten Träger hat, dessen Schnitt mit S eine messbare Menge ergibt.
Ob dies die einzigen möglichen p's sind trau ich mich jetzt nicht zu behaupten. |
|
 |
MI
Anmeldungsdatum: 03.11.2004
Beiträge: 828
Wohnort: München
|
 MI Verfasst am: 17. Sep 2014 13:55 Titel: MI Verfasst am: 17. Sep 2014 13:55 Titel: |
 |
|
Für mich ist die Frage am falschen Ende aufgerollt.
Ich definiere einen Dichteoperator als normierten positiv semi-definiten Spurklasseoperator auf einem Hilbertraum (also \subset \mathcal{B}(\mathcal{H})) ). Als Spurklasseoperator ist der Operator insbesondere kompakt und daher gilt der Spektralsatz für kompakte Operatoren: ). Als Spurklasseoperator ist der Operator insbesondere kompakt und daher gilt der Spektralsatz für kompakte Operatoren:
Es gibt ein Orthonormalsystem  (Eigenvektoren) und eine (abzählbare) Menge (Eigenvektoren) und eine (abzählbare) Menge ) (das Spektrum von (das Spektrum von 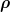 ) sodass ) sodass
} u |u\rangle \langle u|\, du)
Das Spektrum ist dann als abzählbare Menge immer messbar. Auch wenn wir allgemeine beschränkte oder unbeschränkte selbstadjungierte Operatoren zulassen, ändert sich nichts daran, dass deren Spektrum messbar ist.
Die Antwort wäre also: Man schreibt den Dichteoperator nicht einfach in der Integralform auf, diese stammt aus dem Spektralsatz, wo die Messbarkeit aller Mengen garantiert ist.
Alternativ kannst du Dichteoperatoren natürlich als normierte positive Funktionale auf einer C*-Algebra definieren, aber dann hast du die GNS-Konstruktion und gelangst zu Spurklasseoperatoren auf einem Hilbertraum und erst da macht die Integralbeschreibung meines Wissens nach Sinn.
Auf allgemeinen Kegeln kenne ich mich nicht ganz so aus, sollte aber alles ähnlich aussehen, weil die Spektraltheoreme ähnlich sind (müsste ich aber nachschauen).
Gruß
MI |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 17. Sep 2014 13:59 Titel: TomS Verfasst am: 17. Sep 2014 13:59 Titel: |
 |
|
Du hast wohl recht.
Machen wir's noch einfacher. Nehmen wir einen zwei-dim. Hilbertraum. Dieser enthält die S². Auf dieser existiere eine nicht-messbare Teilmenge T (das wissen wir von Banach-Tarski). Nun "schreiben wir eine Matrix hin"

Das Flächenelement dS, die Funktion a sowie die Einheitsvektoren e sind Funktionen der Winkel.
Offensichtlich existiert T, jedoch wg. der fehlenden Messbarkeit nicht das Integral und damit auch nicht die Matrix A.
Was bedeutet das physikalisch? z.B. für ein Spinsystem?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Sep 2014 14:19 Titel: index_razor Verfasst am: 17. Sep 2014 14:19 Titel: |
 |
|
In der Spektraldarstellung integrierst du über das Spektrum von A. Ich verstehe nicht, wieso da ein Integral über eine Teilmenge von  bei dir auftaucht. Das Spektrum von Observablen ist im allgemeinen eine abgeschlossene Teilmenge von R, sollte also stets Lebesgue-meßbar sein, oder nicht? bei dir auftaucht. Das Spektrum von Observablen ist im allgemeinen eine abgeschlossene Teilmenge von R, sollte also stets Lebesgue-meßbar sein, oder nicht? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 17. Sep 2014 15:42 Titel: TomS Verfasst am: 17. Sep 2014 15:42 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | In der Spektraldarstellung integrierst du über das Spektrum von A. Ich verstehe nicht, wieso da ein Integral über eine Teilmenge von  bei dir auftaucht. Das Spektrum von Observablen ist im allgemeinen eine abgeschlossene Teilmenge von R, sollte also stets Lebesgue-meßbar sein, oder nicht? bei dir auftaucht. Das Spektrum von Observablen ist im allgemeinen eine abgeschlossene Teilmenge von R, sollte also stets Lebesgue-meßbar sein, oder nicht? |
Habe ich da was übersehen?
Zunächst hat mich der Dichteoperator interessiert. Für diesen muss ich kein VONS und keine Spektraldarstellung nutzen sondern kann eine beliebige vollständige oder übervollständige Menge von nicht notwendigerweise orthogonalen Einheitsvektoren zugrundelegen. Genau das tue ich hier.
Es war irreführend, jetzt wieder A einzuführen. Ich meine natürlich weiterhin rho.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 17. Sep 2014 15:56 Titel: TomS Verfasst am: 17. Sep 2014 15:56 Titel: |
 |
|
Also nochmal zum zweidimensionalen Beispiel

Natürlich kann ich zunächst eine Orthonormalbasis benutzen, also sowas wie

Aber ich weiß, dass auch andere Vektoren zulässig sind, die nicht mehr orthogonal, jedoch weiterhin normiert und vollständig sein müssen:

So wie ich da sehe, kann das Vektorsystem auch über-vollständig sein, d.h. auch

ist zulässig.
Und von da aus ist es kein großer Schritt zu einem Integral.
Ich gebe aber zu, dass meine Idee sehr weithergeholt erscheinen mag ...
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
 bassiks Verfasst am: 17. Sep 2014 15:57 Titel: bassiks Verfasst am: 17. Sep 2014 15:57 Titel: |
 |
|
| Zitat: | | Zunächst hat mich der Dichteoperator interessiert. Für diesen muss ich kein VONS und keine Spektraldarstellung nutzen sondern kann eine beliebige vollständige oder übervollständige Menge von nicht notwendigerweise orthogonalen Einheitsvektoren zugrundelegen. |
...und die Abbildung p (bzw. a)! Bei geeigneter Wahl von p/a klappt das, ansonsten ist die Domäne des Operators leer und er existiert nicht oder sehe ich das falsch?
Was dies physikalisch bedeutet? Vllt. dass es schwer wird diesen Zustand zu präperieren?  |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 17. Sep 2014 16:04 Titel: TomS Verfasst am: 17. Sep 2014 16:04 Titel: |
 |
|
| bassiks hat Folgendes geschrieben: | | Bei geeigneter Wahl von p klappt das, ansonsten ist die Domäne des Operators leer und er existiert nicht oder sehe ich das falsch? |
Wenn T nicht messbar ist, dann existiert das Inegral und damit rho für kein p. Ich frage wirklich nur danach, was die Menge von Vektoren, die ich mittels T beschreibe, für Anforderungen erfüllen muss und was diese Menge zunächst bedeutet
1) VONS - OK
2) abzählbares VNS - auch OK
3) überabzählbares verallgemeinertes VONS - OK (zumindest im Distributionssinn)
4) mein Konsstrukt - ???
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Sep 2014 16:26 Titel: index_razor Verfasst am: 17. Sep 2014 16:26 Titel: |
 |
|
Ich bin komplett abgehängt. Ich hatte verstanden, daß du nach der Existenz der Spektralzerlegung für Spurklasseoperatoren fragst. So wie ich MIs Antwort oben interpretiere, hatte er es auch so verstanden. Jetzt verstehe ich überhaupt nicht mehr, wonach du eigentlich fragst: ob man einen irgendwie definierten Spurklasseoperator als Integral über nicht-meßbare Mengen im Hilbertraum schreiben kann?
Warum sollte die Antwort darauf irgendwelche physikalischen Konsequenzen haben? Die Frage erscheint mir auch irgendwie widersprüchlich. Kannst du genauer erklären von was für einer Darstellung du eigentlich sprichst? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 17. Sep 2014 16:53 Titel: TomS Verfasst am: 17. Sep 2014 16:53 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Ich hatte verstanden, daß du nach der Existenz der Spektralzerlegung für Spurklasseoperatoren fragst. |
Dann war das ein Missverständnis. Dichteoperatoren gestatten eine allgemeinere Zerlegung.
| index_razor hat Folgendes geschrieben: | | ob man einen irgendwie definierten Spurklasseoperator als Integral über [ggf.] nicht-meßbare Mengen im Hilbertraum schreiben kann? |
sozusagen
| index_razor hat Folgendes geschrieben: | | Kannst du genauer erklären von was für einer Darstellung du eigentlich sprichst? |
Ich versuch's, aber ich sortiere erst mal meine Gedanken; danke für's Verständnis.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 17. Sep 2014 17:52 Titel: Re: Dichteoperator - Spurklasse und Messbarkeit TomS Verfasst am: 17. Sep 2014 17:52 Titel: Re: Dichteoperator - Spurklasse und Messbarkeit |
 |
|
Also, ich versuch’s nochmal von vorne.
Gegeben sei eine zunächst abzählbare Menge von normierten Zuständen

die vollständig, jedoch nicht zwingend orthogonal sein müssen. D.h. wir haben sicher

Für einen Dichteoperator existiert dann die Darstellung

(1) Dabei bezeichnet p_u die (klassische) Wahrscheinlichkeit, dass das System im Zustand |u> vorliegt. Diese berechnet man mittels des Projektors auf |u>, d.h.
 = \text{tr}(P_u \rho) )
Erwähnenswert ist evtl. noch, dass man (1) erweitern kann für mehrdimensionale Unterräume (wobei dann auf orthogonale Unterräume projiziert werden muss)
(2) Für weitere Observablen folgt der Erwartungswert
 )
Natürlich müssen außerdem alle weiteren Anforderungen an einen Dichteoperator erfüllt sein, d.h.
(3) selbstadjungiert
(4) positiv semidefinit
(5) Spurklasse mit Spur gleich 1
Nun möchte ich zwei Verallgemeinerungen durchführen. Hier zunächst die erste (die zweite erst nach Abschluss).
Weil die |u> nicht notwendig orthogonal sein müssen und weil ich für andere Probleme überabzählbare Zustände verwenden kann, bin ich auf die Idee gekommen, diese beiden Ideen für den Dichteoperator zu kombinieren. D.h. jetzt betrachte ich
\,|u\rangle\langle u|)
Dabei sei S eine messbare Menge mit einem geeigneten Maß. Um auf bekanntem Gelände zu bleiben könnte man z.B. kohärente Zustände betrachten, d.h.

Das Maß wäre dann soetwas wie

auf der komplexen u-Ebene. Wie man sieht hat dies nichts mit einer Spektralzerlegung zu tun.
Dabei stellt sich nun im Wesentlichen die Frage, ob dies mathematisch möglich und physikalisch sinnvoll ist, d.h. insbs. ob die Punkte (1) – (5) weiterhin gültig bleiben.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 18. Sep 2014 06:49, insgesamt 2-mal bearbeitet |
|
 |
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
 bassiks Verfasst am: 17. Sep 2014 18:30 Titel: bassiks Verfasst am: 17. Sep 2014 18:30 Titel: |
 |
|
Ok. Tut mir leid. Ich hab dich völlig falsch verstanden.
Was deine Frage betrifft, so meine ich zu wissen dass eine überabzählbare Folge von Einheitsvektoren ausreichend ist. Ich bin eben noch am Suchen nach einer verlässlichen Quelle.
Auch auf die Gefahr hin dass ich mich hier blamiere: Warum verlangst du Vollständigkeit? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 17. Sep 2014 18:47 Titel: TomS Verfasst am: 17. Sep 2014 18:47 Titel: |
 |
|
| bassiks hat Folgendes geschrieben: | | Warum verlangst du Vollständigkeit? |
Wäre die Vollständigkeit nicht gegeben, dann könnte ich nicht alle möglichen Zustände beschreiben.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
 bassiks Verfasst am: 17. Sep 2014 18:55 Titel: bassiks Verfasst am: 17. Sep 2014 18:55 Titel: |
 |
|
|
Dann hab ich dich wieder falsch verstanden. Dachte du willst nur wissen was man für einen Dichteoperator mindestens benötigt. Wenn du alle möglichen Zustände damit beschreiben willst, dann ist natürlich Vollständigkeit gefragt... |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 17. Sep 2014 18:59 Titel: TomS Verfasst am: 17. Sep 2014 18:59 Titel: |
 |
|
Ich denke, speziell für kohärente Zustände genügt es zu zeigen, dass für jeden Dichteoperator (unter der Verwendung der Eigenzustände des harmonischen Oszillators)

eine Darstellung (unter Verwendung kohärenter Zustände)
\,|u\rangle\langle u|)
existiert (u.u.).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 18. Sep 2014 06:44, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Sep 2014 19:50 Titel: index_razor Verfasst am: 17. Sep 2014 19:50 Titel: |
 |
|
Diese "überabzählbaren" Zustände kenne ich nur aus der Spektralzerlegung von Operatoren mit kontinuierlichem Spektrum. Und dann handelt es sich nicht eigentlich um Basiselemente des Hilbertraums, sondern um operatorwertige Maße. Dein Integral
\,|u\rangle\langle u|)
erinnert frappierend an das, was man in diesem Zusammenhang als den Operator ) zu bezeichnen pflegt, wobei zu bezeichnen pflegt, wobei } u |u\rangle\langle u|\dd u) . .
Hier wird jeweils nur über das (meßbare) Spektrum von T integriert.
Ist leider alles, was mir im Augenblick dazu einfällt. Wenn dir was anderes vorschwebt, ist mir noch nicht so richtig klar, was. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 17. Sep 2014 19:54 Titel: TomS Verfasst am: 17. Sep 2014 19:54 Titel: |
 |
|
Das meine ich nicht.
Ich meine wirklich z.B. kohärente Zustände (diese sind überabzählbar und über-vollständig über C). Und ich meine nicht-ONS für Dichteoperatoren.
Schau mal hier: http://en.m.wikipedia.org/wiki/Coherent_state#Mathematical_features_of_the_canonical_coherent_states
Wichtig: eigtl. ist das nur ein Beispiel, und es geht mir um Dichteoperatoren, nicht um reine Zustände
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 17. Sep 2014 23:52 Titel: TomS Verfasst am: 17. Sep 2014 23:52 Titel: |
 |
|
Also für kohärente Zustände funktioniert das tatsächlich: Kap. 3.4 und 3.5, insbs. Gl. (3.73) in
http://www.fulviofrisone.com/attachments/article/426/Coherent%20States%20in%20Quantum%20Physics.pdf
Die Eigenschaften (1) - (5) werden weiterhin, ggf. geeignet modifiziert, gültig sein. Ich werde das auch noch mal für andere kontinuierliche Systeme S überprüfen.
Damit ist die erste Verallgemeinerung der Dichtematrix abgeschlossen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 18. Sep 2014 10:40 Titel: index_razor Verfasst am: 18. Sep 2014 10:40 Titel: |
 |
|
Ich denke, was du meinst ist nichts wesentlich anderes, als was ich geschrieben habe. (Auch die beiden Links scheinen erstmal von nichts anderem zu sprechen, auch wenn ich jetzt wieder nicht verstehe, was deine urpsrüngliche Frage mit einer "Verallgemeinerung der Dichtematrix" zu tun hatte.) Ich weiß zwar nicht ob es in diesem Fall technisch so problemlos durchführbar ist, wie im Fall von normalen Operatoren. Aber wenn du von kohärenten Zuständen sprichst, geht es ja erstmal nur um das Spektrum und die "verallgemeinerten Eigenzustände" des Vernichtungsoperators 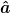 . .
Im Zusammenhang mit dem statistischen Operator physikalisch relevant scheint mir nun also erstmal die Frage, ob für Vernichtungsoperatoren ein meßbarer Funktionalkalkül definiert werden kann, der es erlaubt zu einer Wahrscheinlichkeitsdichte ) über dem (nun eben komplexen) Spektrum von über dem (nun eben komplexen) Spektrum von 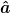 einen Operator einen Operator ) zu definieren, dessen Eigenwerte auf kohärenten Zuständen gerade die Wahrscheinlichkeit ergibt, daß sich das System in diesem Zustand befindet, also zu definieren, dessen Eigenwerte auf kohärenten Zuständen gerade die Wahrscheinlichkeit ergibt, daß sich das System in diesem Zustand befindet, also |\alpha\rangle\dd \alpha = p(\alpha)|\alpha\rangle\dd\alpha) . Im Falle von gewöhnlichen Observablen führt genau diese Frage auf die Definition von Spektralmaßen (als verallgemeinerte Eigenzustände) und das Spektraltheorem. (Das entscheidende für die Interpretation von Eigenzuständen von . Im Falle von gewöhnlichen Observablen führt genau diese Frage auf die Definition von Spektralmaßen (als verallgemeinerte Eigenzustände) und das Spektraltheorem. (Das entscheidende für die Interpretation von Eigenzuständen von  als physikalische Zustände, ist denke ich aber die Existenz des Funktionalkalküls, nicht unbedingt das Spektralmaß.) Ob ein solches Maß in diesem Fall definiert werden kann, weiß ich wie gesagt nicht, aber deine beiden Quellen scheinen genau dies anzunehmen (oder vorauszusetzen). Oder was soll als physikalische Zustände, ist denke ich aber die Existenz des Funktionalkalküls, nicht unbedingt das Spektralmaß.) Ob ein solches Maß in diesem Fall definiert werden kann, weiß ich wie gesagt nicht, aber deine beiden Quellen scheinen genau dies anzunehmen (oder vorauszusetzen). Oder was soll  anderes sein als ein Operatormaß auf dem Spektrum von anderes sein als ein Operatormaß auf dem Spektrum von 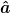 ? ?
Wenn es aber existiert, sollte es auch kein Problem sein jeden Operator, nicht nur den statistischen, in dieser verallgemeinerten Basis in der Form wie in Gl. (3.73) darzustellen. Es sei denn ich übersehe da etwas, aber auf irgendwelche Subtilitäten wird in dem Buch an der Stelle jedenfalls auch nicht hingewiesen. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 18. Sep 2014 10:52 Titel: TomS Verfasst am: 18. Sep 2014 10:52 Titel: |
 |
|
Ich denke, wir sind uns ziemlich einig. Der einzige Punkt, der mir so ohne weiteres nicht klar war, ist folgender: ich kenne den Spektralsatz für selbstadjungierte sowie für normale Operatoren; beides trifft auf die Vernichter jedoch nicht zu, d.h. ich kann nicht einfach den Spektralsatz und alle Schlussfolgerungen übernehmen (mir ist intuitiv schon klar, dass es für kohärente Zustände funktioniert, aber eben nicht gnerell).
Der ursprüngliche Gedanke ging in die Richtung, dass im Falle der Dichtematrix diese direkt mit einem Wahrscheinlichkeitsmaß dafür verknüpft ist, ein System in einem bestimmten (ggf. mehrdimensionalen) Unterraum, zu finden. Ich denke, das passt auch für verallgemeinerte Dichteoperatoren.
Ich denke nochmal über die Nicht-Messbarkeit nach.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 19. Sep 2014 13:10 Titel: TomS Verfasst am: 19. Sep 2014 13:10 Titel: |
 |
|
Nach einigem Nachdenken:
Aufgrund der Separabilität des Hilbertraumes ist grundsätzlich immer eine diskrete, abzählbar unendliche Hilbertbasis möglich. Das Problem der Nichtmessbarkeit tritt gar nicht auf.
Wenn man kontinuierliche Basen verwenden möchte, dann kann man nicht-messbare Mengen künstlich einführen, aber das ist m.E. ohne physikalische Relevanz.
Nochmal zum zweidimensionalen Beispiel. Ich betrachte die Basis


Nun führe ich die kontinuierliche, überabzählbare Basis


\,|\phi\rangle\langle\phi| )
ein. Bei geeigneter Verwendung von delta-Distributionen für p folgt unmittelbar die Darstellung in der abzählbaren Basis. Ich denke, es ist unmittelbar einsichtig, dass das auf endlich-dimensionale Räume und damit auf S^n erweiterbar ist (wobei die Sphäre immer eine Dimension weniger hat als der betrachtete Raum).
D.h. ich schreibe unter Verwendung des Winkel-n-Tupels Omega allgemein
\,|\Omega\rangle\langle\Omega | )
Wenn ich nur ein Teilmenge T betrachte, also
 )
dann ist das gleichbedeutend mit
 )
wobei
 = \begin{cases} p(\Omega) & \text{für } \Omega \subset T \\ 0 & \text{sonst } \end{cases} )
Soweit alles klar.
Jetzt zu meiner eigtl. Frage, was passiert, wenn T eine nicht-messbare Menge ist und was das physikalisch bedeutet. Die Antwort, die ich mir selber gebe, lautet: die kontinuierliche Basis ist aufgrund der Separabilität des Hilbertraumes unnötig, für nicht-messbares T ist das Integral nicht definiert; physikalisch ist das irgendwo zwischen irrelevant und sinnlos.
Also Danke für’s Zuhören und Sorry für die Verwirrung!
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
















