| Autor |
Nachricht |
Hezed
Anmeldungsdatum: 24.02.2016
Beiträge: 5
|
 Hezed Verfasst am: 24. Feb 2016 13:52 Titel: Verständnisproblem: Lokalisationsenergie durch Unschärferela Hezed Verfasst am: 24. Feb 2016 13:52 Titel: Verständnisproblem: Lokalisationsenergie durch Unschärferela |
 |
|
Meine Frage:
LIebe Kollegas, man kann ja nicht alles wissen und verstehen,darum:
Je näher das Elektron dem Atomkern kommt, desto "mehr" ist es lokalisiert, was eine Einschränkung des Ortes bedeutet und damit laut Unschärferelation eine höhere Impulsunschärfe.
Abgesehen davon würde ja ein höherer Impuls eine höhere (klassische) kinetische Energie bedeuten, also (sehr vereinfacht): je näher das Elektron desto höher seine Energie (= Lokalisationsenergie).
Mein Verständnisproblem liegt im Übergang von Impulsunschärfe zur höherem Impuls. Wieso (zum Geier!!!!) bedeutet eine höhere Unschärfe einen höheren Impuls?! DIe Impulsunschärfe bedeutet ja nur, dass die "Impulsmöglichkeit" des Teilchens sich in größeren Grenzen bewegt und nicht der Impuls selbst diese Größe HAT, oder? Nehmen wir die Impulsunschärfe  , das würde doch für den Impuls px bedeuten sein Wert bewegt sich im Bereich +/- 4 und NICHT px IST 4, px könnte genau so 0 sein (Lokalisationsenergie 0 bedeuten würde). , das würde doch für den Impuls px bedeuten sein Wert bewegt sich im Bereich +/- 4 und NICHT px IST 4, px könnte genau so 0 sein (Lokalisationsenergie 0 bedeuten würde).
Ein anderes bzw. ähnliches Argument ist auch der Impuls muss (selbstverständlich) größer als seine Unschärfe sein. NEIN, der Wert eines Parameters und die MÖGLICHKEIT seiner Werte sind ein Unterschied, oder?
Meine Ideen:
Meine einziger eigener Ansatz zur Lösung dieses Problems ist, dass hier beim Impulswert eine Zeitmittel zum Tragen kommt und das sich natürlich bei größerer Unschärfe vergrößert...
Oder (was ich ja eher glaube) ich habe hier irgendwo einen blöden Denkfehler und steh aber sowas von auf dr Leitung...
Vielen Dank schon mal... |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 24. Feb 2016 18:30 Titel: Re: Verständnisproblem: Lokalisationsenergie durch Unschärfe index_razor Verfasst am: 24. Feb 2016 18:30 Titel: Re: Verständnisproblem: Lokalisationsenergie durch Unschärfe |
 |
|
| Hezed hat Folgendes geschrieben: | Mein Verständnisproblem liegt im Übergang von Impulsunschärfe zur höherem Impuls. Wieso (zum Geier!!!!) bedeutet eine höhere Unschärfe einen höheren Impuls?! DIe Impulsunschärfe bedeutet ja nur, dass die "Impulsmöglichkeit" des Teilchens sich in größeren Grenzen bewegt und nicht der Impuls selbst diese Größe HAT, oder?
|
Ja, sozusagen. Unter "höherem Impuls" würde man andererseits ja wahrscheinlich in etwa verstehen, daß Messungen mit einem größeren Impulsbetrag, oder gleichbedeutend mit größerem 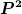 , wahrscheinlicher geworden sind. Das bedeutet dann, daß der Erwartungswert , wahrscheinlicher geworden sind. Das bedeutet dann, daß der Erwartungswert  in diesem Zustand größer ist. Mit der Impulsunschärfe, also dem Erwartungswert in diesem Zustand größer ist. Mit der Impulsunschärfe, also dem Erwartungswert ^2\rangle) hat das nur insofern zu tun, als für lokalisierte Zustände ja der Impuls im Mittel verschwindet, also hat das nur insofern zu tun, als für lokalisierte Zustände ja der Impuls im Mittel verschwindet, also  . Also ist die Impulsunschärfe gleich dem Erwartungswert des Impulsquadrats und damit gleichzeitig ein Maß dafür, wie groß der Impuls in diesem lokalisierten Zustand ist. . Also ist die Impulsunschärfe gleich dem Erwartungswert des Impulsquadrats und damit gleichzeitig ein Maß dafür, wie groß der Impuls in diesem lokalisierten Zustand ist. |
|
 |
Hezed
Anmeldungsdatum: 24.02.2016
Beiträge: 5
|
 Hezed Verfasst am: 25. Feb 2016 16:16 Titel: Hezed Verfasst am: 25. Feb 2016 16:16 Titel: |
 |
|
Hm, danke, ich glaub jetz hab ichs. Könnte man das Ganze so ausdrücken:
H-Atom, das Elektron befindet sich im Anziehungsbereich des Atomkerns. Der Impuls des Elektrons ist in bestimmten Grenzen unbestimmt, ganz klassisch gesagt das Elektron-Teilchen hat in diesen Grenzen immer einen anderen Impuls. Hat es gerade zufällig einen hohen Impulsbetrag, ist die Lokalisationsenergie etwas höher und das Elektron etwas weiter weg vom Kern. Hat es aber gerade zufällig einen etwas niedrigeren Implusbetrag ist es demnach etwas näher am Kern. Und die zu dieser Impulsschärfe zugehörige Ortsunschärfe (in Verbindung mit der Anziehung durch den positiv geladenen Kern) ergibt quasi den "Aufenthaltsort" des Elektrons an.
Oder so: der Ewartungswert/Mittelwert des Impulsbetrages ist höher und damit auch der Erwartungswert/Mittelwert der Energie des Elektrons.
Also ich denke ich verstehe nun wieso größere Impulsunschärfe auch größeren (mittleren) Impuls bedeutet, was ich aber noch nicht verstehe ist die Argumentation in den beiden Zitaten unten, wieso p ≈ ∆p oder überhaupt p ≥ ∆p.
"Feynman unternimmt nun folgende Argumentation: Ein Elektron sei in einem Bereich ∆x = a um das Proton lokalisiert. Damit ist der Impuls des Teilchens mindestens von der Größenordnung seiner Unschärfe, p ≈ ∆p = h/a."
(http://frhewww.physik.uni-freiburg.de/SideBar/l5_Lectures/SS2011/Skripte/Textskript/Skript_03_SS2011-ExIV-HELM.pdf, 26.2.2016)
oder in einem Schulbuch: "Wenn man also ein Teilchen ´einsperrt´, dann erhöht sihc zwangsläufig sein Impuls p, denn dieser kann natürlich nicht kleiner sein als die Impulsunschärfe: p ≥ ∆p."
(Apolin M. (2008). Big Bang. Physik 7. Wien: öbv.)
EDIT:
Oh, stopp, ich hab beim Schreiben deine Antwort aus dem Blick verloren...
Wenn ich deine Antwort recht verstehe ist die Impulsunschärfe definiert als quasi die Standardabweichung/Varianz/Mittelwert der Abstandsquadrate des Impulses, und da der Mittelwert des Impulses 0 ist, ist natürlich der Mittelwert des Impulsbetrages in der Größenordnung der Impulsunschärfe.
Das würde bedeuten, dass in den oben erwähnten Zitaten eigentlich richtiger Weise stehen müsste: <p²> ≈ ∆p² , oder? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 25. Feb 2016 19:20 Titel: index_razor Verfasst am: 25. Feb 2016 19:20 Titel: |
 |
|
| Hezed hat Folgendes geschrieben: |
Also ich denke ich verstehe nun wieso größere Impulsunschärfe auch größeren (mittleren) Impuls bedeutet, was ich aber noch nicht verstehe ist die Argumentation in den beiden Zitaten unten, wieso p ≈ ∆p oder überhaupt p ≥ ∆p.
|
Ich interpretiere mal ein bißchen:
| Zitat: |
"Feynman unternimmt nun folgende Argumentation: Ein Elektron sei in einem Bereich ∆x = a um das Proton lokalisiert. Damit ist der Impuls des Teilchens mindestens von der Größenordnung seiner Unschärfe, p ≈ ∆p = h/a."
(http://frhewww.physik.uni-freiburg.de/SideBar/l5_Lectures/SS2011/Skripte/Textskript/Skript_03_SS2011-ExIV-HELM.pdf, 26.2.2016)
|
 ist nicht gleich ist nicht gleich 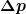 , sondern was der Autor eigentlich schreiben wollte ist, daß h/a ungefähr die Untergrenze für die Impulsunschärfe , sondern was der Autor eigentlich schreiben wollte ist, daß h/a ungefähr die Untergrenze für die Impulsunschärfe 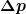 ist (ungefähr, weil es ja statt h eigentlich ist (ungefähr, weil es ja statt h eigentlich  heißen müßte) und letztere ein exaktes Maß für die "größe des Impulses p" ist. Also eigentlich müßte da sowas stehen wie heißen müßte) und letztere ein exaktes Maß für die "größe des Impulses p" ist. Also eigentlich müßte da sowas stehen wie

Ich hoffe, was danach in dem Skript kommt, ergibt damit dann noch halbwegs Sinn. Welchen Sinn es ergeben könnte, fasse ich aus meiner Sicht unten nochmal zusammen.
| Zitat: |
oder in einem Schulbuch: "Wenn man also ein Teilchen ´einsperrt´, dann erhöht sihc zwangsläufig sein Impuls p, denn dieser kann natürlich nicht kleiner sein als die Impulsunschärfe: p ≥ ∆p."
(Apolin M. (2008). Big Bang. Physik 7. Wien: öbv.)
|
Läuft wahrscheinlich auf was ähnliches hinaus. Man muß aber m.E. schon sehr gutmütig interpretieren, um da einen plausiblen Sinn reinzuprügeln. Der Wert einer Zufallsgröße ist nicht "natürlich" größer oder gleich ihrer Unschärfe. Warum sollte das gelten?
| Zitat: |
EDIT:
Oh, stopp, ich hab beim Schreiben deine Antwort aus dem Blick verloren...
Wenn ich deine Antwort recht verstehe ist die Impulsunschärfe definiert als quasi die Standardabweichung/Varianz/Mittelwert der Abstandsquadrate des Impulses, und da der Mittelwert des Impulses 0 ist, ist natürlich der Mittelwert des Impulsbetrages in der Größenordnung der Impulsunschärfe.
Das würde bedeuten, dass in den oben erwähnten Zitaten eigentlich richtiger Weise stehen müsste: <p²> ≈ ∆p² , oder? |
Vergessen wir mal den Mittelwert des Impulsbetrages.
Was wir eigentlich wollten ist eine Abschätzung der Bewegungsenergie des Teilchens in Abhängigkeit von seiner Ortsunschärfe, richtig? Nun wissen wir, daß wir es mit einem gebundenen Zustand zu tun haben, für den  gilt. Also gilt. Also ^2 =\langle P^2\rangle) . Die gesuchte Bewegungsenergie hat also im Mittel den Wert . Die gesuchte Bewegungsenergie hat also im Mittel den Wert
^2
<br />
)
Soweit haben wir noch gar nichts abgeschätzt. Alles gilt exakt unter der Bedingung, daß der Impuls im Mittel verschwindet. Desweiteren können wir den mittleren Aufenthaltsort des Teilchens in den Ursprung verlegen und dann die Unschärferelationen in der folgenden Form benutzen

aus der folgt für die Doppelsumme über i und k:

Also

Das ist also die allgemeinste aus der Unschärferelation folgende Abschätzung für die Bewegungsenergie eines gebundenen Teilchens in Abhängigkeit von seiner Ortsunschärfe. Wie alle Unschärferelationen liefert sie zunächst nur eine Untergrenze. Wenn man aber voraussetzen kann, daß die Wahrscheinlichkeit hoher Energien hinreichend schnell abnimmt, liefert es sicher auch eine Abschätzung der Größenordnung der Energie selbst. Das müßte man aber sicher im Einzelfall genauer untersuchen. |
|
 |
Hezed
Anmeldungsdatum: 24.02.2016
Beiträge: 5
|
 Hezed Verfasst am: 26. Feb 2016 20:23 Titel: Hezed Verfasst am: 26. Feb 2016 20:23 Titel: |
 |
|
Hm...die letzten Zeilen konvergieren dann schon erstaunlich schnell gegen meinen Horizont  - trotzdem Danke, die Grundzüge kapier ich. - trotzdem Danke, die Grundzüge kapier ich.
Im Wesentlichen gings bei meiner Frage darum, dass ich aus der Unschärferelation gern den Grund (den Bohr nicht liefern konnte) für die Stabilität des Atoms - also die Lokalisationsenergie - folgern möchte, und das für 17-jährige.
Neu für mich war, dass die Impulsunschärfe ∆p nicht den gesamten möglichen Impulsbereich abdeckt, sondern nur als die Standarsabweichung (stimmt doch, oder?) des Impulses, also (∆p)² = <(p - <p>)²> definiert ist. Ist aber auf der anderen Seite ja auch klar, weil die Wahrscheinlichkeit für höhere Impulse sicher kontinuierlich abnimmt, und damit müsste dann ∆p ja unendlich groß sein ...
Mit <p> = 0 gilt dann natürlich (∆p)² = <p²>.
Also heißt das auf gut Deutsch, je größer die Impulsunschärfe, desto größer wird der mittlere Impuls und damit auch die Lokalisationsenergie des Elektrons.
Und formelmäßig lässt sich dann p ~ ∆p setzen und begründen, und für 17-jährige ist das genau genug denke ich.
Nur eins ist mir noch nicht klar (sorry wenn ich auf den Feinheiten da herumreit...):
Wieso kannst du  schreiben, das gilt doch nur für den Erwartungswert Wurzel( <p²> ) laut obigem? schreiben, das gilt doch nur für den Erwartungswert Wurzel( <p²> ) laut obigem? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 27. Feb 2016 17:06 Titel: index_razor Verfasst am: 27. Feb 2016 17:06 Titel: |
 |
|
| Hezed hat Folgendes geschrieben: | Hm...die letzten Zeilen konvergieren dann schon erstaunlich schnell gegen meinen Horizont  - trotzdem Danke, die Grundzüge kapier ich. - trotzdem Danke, die Grundzüge kapier ich.
|
Auch wenn es nur Details sind, würde mich interessieren was unklar geblieben ist.
| Zitat: |
Im Wesentlichen gings bei meiner Frage darum, dass ich aus der Unschärferelation gern den Grund (den Bohr nicht liefern konnte) für die Stabilität des Atoms - also die Lokalisationsenergie - folgern möchte, und das für 17-jährige.
|
Hm, also wir wissen nun, je stärker das Elektron lokalisiert ist, desto größer ist seine kinetische Energie. Ein Argument für die Stabilität des Atoms ist das aber ohne weiteres noch nicht. Es ist nicht mal ein Argument für die schwächere Behauptung, daß das Elektron stets einen minimalen mittleren Abstand vom Zentrum besitzt.
Es ist z.B. denkbar, daß der Verlust an potentieller Energie bei Annäherung an das Zentrum teilweise durch einen Gewinn an kinetischer Energie wieder ausgeglichen wird und die elektromagnetische Strahlung lediglich den Überschuß  abtransportiert. Das ist z.B. genau das Verhalten was nach klassischer Rechnung für ein geladenes Teilchen im Coulomb-Potential auf näherungsweise kreisförmigen Orbits zu erwarten wäre. abtransportiert. Das ist z.B. genau das Verhalten was nach klassischer Rechnung für ein geladenes Teilchen im Coulomb-Potential auf näherungsweise kreisförmigen Orbits zu erwarten wäre.
Es wäre auch eher überraschend, wenn man ein allgemeingültiges Argument für die Stabilität allein aus der Ort-Impuls-Unschärferelation konstruieren könnte ohne auch nur die Art der Wechselwirkung auf das Teilchen in Betracht zu ziehen. Würde man damit nicht auch zuviel beweisen? Es gibt ja auch elektromagnetische Bindungszustände, die quantenmechanisch instabil sind, z.B. Positronium. Für diese gelten aber dieselben Orts-Impuls-Unschärferelationen.
Ein stichhaltiges Argument für die Stabilität eines quantenmechanischen Zustands wird weniger aus der Abschätzung seiner mittleren Energie gewonnen, als aus der Breite seiner Energieverteilung. Eine Variante davon führt auf die diversen Energie-Zeit-Unschärferelationen. Diese liefern zwar kein allgemeingültiges Argument für die Stabilität, aber eine Abschätzung für die Untergrenze der Lebensdauer eines Zustands in Abhängigkeit von seiner Energieunschärfe.
| Zitat: |
Neu für mich war, dass die Impulsunschärfe ∆p nicht den gesamten möglichen Impulsbereich abdeckt, sondern nur als die Standarsabweichung (stimmt doch, oder?) des Impulses, also (∆p)² = <(p - <p>)²> definiert ist.
|
Ja, das stimmt so.
| Zitat: |
Ist aber auf der anderen Seite ja auch klar, weil die Wahrscheinlichkeit für höhere Impulse sicher kontinuierlich abnimmt, und damit müsste dann ∆p ja unendlich groß sein ...
Mit <p> = 0 gilt dann natürlich (∆p)² = <p²>.
Also heißt das auf gut Deutsch, je größer die Impulsunschärfe, desto größer wird der mittlere Impuls und damit auch die Lokalisationsenergie des Elektrons.
|
Ja, mit dem Vorbehalt, daß "mittlerer Impuls" hier eben mehrdeutig ist. Der technisch einwandfreie Begriff ist "zweites absolutes Moment des Impulses", bzw. dessen Wurzel. Der mittlere Impuls (Vektorgröße) ist ja eben null. Das erste absolute Moment wäre auch nicht null, wird aber in dem Zusammenhang nicht verwendet. Könnte man aber bestimmt tun und sich dann vermutlich über etwas andere Ungleichungen und Abschätzungen freuen.
| Zitat: |
Nur eins ist mir noch nicht klar (sorry wenn ich auf den Feinheiten da herumreit...):
Wieso kannst du  schreiben, das gilt doch nur für den Erwartungswert Wurzel( <p²> ) laut obigem? schreiben, das gilt doch nur für den Erwartungswert Wurzel( <p²> ) laut obigem? |
Das war nur meine Interpretation dessen, was in den Zitaten mit "dem Impuls p" gemeint sein könnte, so daß sich alles aus meiner Sicht zusammenreimt. Da die Autoren nicht explizit geäußert haben, was sie unter "dem Impuls" verstehen, habe ich mir die Freiheit genommen  zu setzen. Dies stimmt dann exakt mit zu setzen. Dies stimmt dann exakt mit 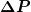 , also der Impulsunschärfe des Zustands, überein, da der mittlere Impuls verschwindet. Mehr steckte jetzt nicht dahinter. , also der Impulsunschärfe des Zustands, überein, da der mittlere Impuls verschwindet. Mehr steckte jetzt nicht dahinter. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
 TomS Verfasst am: 28. Feb 2016 07:26 Titel: TomS Verfasst am: 28. Feb 2016 07:26 Titel: |
 |
|
Aus der Unschärfenrelation alleine kann sicher kein Argument für die Stabilität eines Zustandes abgeleitet werden.
Bsp. Kernphysik: zwischen einem Proton und einem Neutron (zischen zwei Neutronen) liegt ein stark (schwach) anziehende Kraft vor. Dennoch existiert zwar das Deuteron, jedoch nicht das Di-Neutron als gebundener Zustand.
Man muss m.E. zwingend die Schrödingergleichung (o.a. Gleichungen lösen). Aus der Unschärfenrelation alleine folgt lediglich - unter der Voraussetzung der Existenz eines gebundenen Zustandes - die Größenordnung für Größe und Energie.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Hezed
Anmeldungsdatum: 24.02.2016
Beiträge: 5
|
 Hezed Verfasst am: 02. März 2016 16:28 Titel: Hezed Verfasst am: 02. März 2016 16:28 Titel: |
 |
|
@index_razor:
| index_razor hat Folgendes geschrieben: | Auch wenn es nur Details sind, würde mich interessieren was unklar geblieben ist.
|
Nein inzwischen hab ichs quasi, is schon a bissl lang her bei mir, dass ich das gelernt hab, aber die  müssten für die einzelnen Raumrichtungen stehen oder Ähnliches ... ist aber echt nicht so wichtig, die Grundidee versteh ich, und in diese Tiefe kann ich mich allein schon aus Zeitgründen leider nicht mehr stürzen... an der Uni hatten wir als Lehramtskandidaten die Quantenmechanik auch nur als Mini-Einführungsvorlesung zu absolvieren ... müssten für die einzelnen Raumrichtungen stehen oder Ähnliches ... ist aber echt nicht so wichtig, die Grundidee versteh ich, und in diese Tiefe kann ich mich allein schon aus Zeitgründen leider nicht mehr stürzen... an der Uni hatten wir als Lehramtskandidaten die Quantenmechanik auch nur als Mini-Einführungsvorlesung zu absolvieren ...
-----
Und bezüglich meines Problems: Da wollte ich wohl etwas zu viel, aber was mich wundert ist, dass ich nicht mal sagen kann, dass auf Grund der Unschärferelation (bzw. der daraus folgenden Lokalisationsenergie) das Elektron nicht auf das Proton "stürzt", zumindest habe ich diesen Punkt von dir index_razor so verstanden:
| index_razor hat Folgendes geschrieben: | | Es ist nicht mal ein Argument für die schwächere Behauptung, daß das Elektron stets einen minimalen mittleren Abstand vom Zentrum besitzt. |
Nicht einmal für den einfachsten Fall, nur ein Proton und ein Elektron?
An und für sich hat sich das Argument, dass wenn das Elektron in den Kern stürzen würde, es "komplett" lokalisiert ist, und damit einen extrem großen Impuls haben müsste, was dem Verweilen im/am Proton widersprechen würde, sehr gut angehört.
Lässt sich das Argument unter der Vorraussetzung extremer Vereinfachung oder einfachster Verbildlichung irgendwie halten?
Oder gibt es ein einfaches, sehr anschauliches Argument? Die Schrödingergleichung zu lösen fällt hier leider ein bissi aus dem Rahmen (meinem und denm der Schüler) hinaus... |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
 TomS Verfasst am: 02. März 2016 21:28 Titel: TomS Verfasst am: 02. März 2016 21:28 Titel: |
 |
|
Ich habe das oben schon geschrieben: man kommt m.E. nicht um die Betrachtung der Schrödingergleichung herum.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Hezed
Anmeldungsdatum: 24.02.2016
Beiträge: 5
|
 Hezed Verfasst am: 02. März 2016 22:56 Titel: Hezed Verfasst am: 02. März 2016 22:56 Titel: |
 |
|
|
Alles klar, danke! |
|
 |
TAppel
Anmeldungsdatum: 21.02.2016
Beiträge: 13
|
 TAppel Verfasst am: 02. März 2016 23:14 Titel: TAppel Verfasst am: 02. März 2016 23:14 Titel: |
 |
|
Hmm, wenn es nur darum geht, dass das Elektron nicht in den Kern fällt, kann man auch ohne komplette Auflösung der S.-Gleichung sagen, dass rein mathematisch Elektronen nur als Welle dargestellt werden und die S.-Gleichung unter dieser Prämisse (und nicht unter der Vorstellung zweier sich umkreisender Teilchen) aussagt, dass die elektrostatische Kraft Elektronen nicht unter ein gewisses Energie-Niveau "zwingen" kann.
_________________
Wichtig ist, dass wie niemals aufhören zu fragen." -Albert Einstein |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
 TomS Verfasst am: 03. März 2016 00:10 Titel: TomS Verfasst am: 03. März 2016 00:10 Titel: |
 |
|
| TAppel hat Folgendes geschrieben: | | ... wenn es nur darum geht, dass das Elektron nicht in den Kern fällt, kann man auch ohne komplette Auflösung der S.-Gleichung sagen, dass ... die elektrostatische Kraft Elektronen nicht unter ein gewisses Energie-Niveau "zwingen" kann. |
Nein, das kann man i.A. nicht.
Betrachten wir ein Wellenpakte psi in einem anziehenden Potential der Form
 = -\frac{a}{r^n})
Der mathematisch problematische Anteil der Energie stammt sicher aus der potentiellen Energie. Deren Erwartungswert folgt aus
\,|\psi(r)|^2 = -4a\pi \int_0^\infty \frac{dr}{r^{n-2}}\,|\psi(r)|^2)
Unter der Annahme, dass die Wellenfunktion genügend schnellt fällt, stammt der dominierende Teil sicher aus dem konstanten Wert der Wellenfunktion am Ursprung und aus dessen Beitrag in einem endlichen Volumen
\,|\psi(r)|^2 = -4a\pi |\psi_0|^2 \int_0^R \frac{dr}{r^{n-2}})
Nun beobachtet man etwas seltsames.
Für das Coulombpotential mit n = 1 hat dieses Integral für eine am Ursprung nicht verschwindende Wellenfunktion einen endlichen Wert.
Für große n divergiert das Integral jedoch, es sei denn, dass die Wellenfunktion am Ursprung genügend schnell verschwindet, d.h. sich verhält wie
 \simeq r^k)
für geeignetes k.
Daraus folgt, dass für große n entweder
i) die Wellenfunktion am Ursprung verschwindet und daher ihr Maximum für größere r hat - entgegen der Anschauung, dass ein stärker anziehendes Potential als das Coulombpotential die Wellenfunktion stärker lokalisiert,
ii) oder dass der Hamiltonoperator ein nach unten unbeschränktes Spektrum hat, dass also tatsächlich

Im Falle von (ii) hilft die Unschärfenrelation also nicht.
Die dritte, sehr technische Möglichkeit ist, dass der so definierte Hamiltonoperator nicht selbstadjungiert (für geeignete Randbedingungen bei r = 0) definiert werden kann und damit unphysikalisch ist.
Jedenfalls hilft die Unschärfenrelation alleine nicht. Man muss das Potential bzw. die Schrödingergleichung betrachten.
EDIT: kennt sich jemand mit diesen Potentialen 1/r^n aus? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
 TomS Verfasst am: 03. März 2016 01:10 Titel: TomS Verfasst am: 03. März 2016 01:10 Titel: |
 |
|
Nochmal eher mit dem Blickwinkel der Unschärfenrelation.
Betrachten wir wieder ein bei r = 0 lokalisiertes Wellenpaket mit
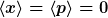
Dann ist


Nun ist jedoch außerdem
)
Für ein wohldefiniertes, lokalisiertes Wellenpaket sind beide Erwartungswerte für x^2 und p^2 endlich. Beide sind außerdem unabhängig von der speziellen Form von V. Betrachtet man jedoch das o.g. V(r) ~ -1/r^n so wird <V> u.U. negativ unendlich und damit der für -<V> positiv unendlich. Da der Erwartungswert für p^2 endlich und positiv ist, muss der Erwartungswert für <E> negativ unendlich sein, d.h. das Wellenpaket hat eine nach unten unbeschränkte negative Energie. Alternativ ist <V> negativ, jedoch endlich. Um dies zu erreichen muss, wie oben hergeleitet, die Wellenfunktion bei r = 0 wird r^k verschwinden. Damit wäre das Potential -1/r^n bei r = 0 "repulsiv".
Während also die Unschärfenrelation ein physikalisch vernünftiges, bei r = 0 lokalisiertes Wellenpaket zulässt, modifiziert das Potential ~ -1/r^n das Problem so, dass es entweder physikalisch unsinnig mit E nach unten unbeschränkt = ohne Grundzustand wird, oder dass das Potential repulsiv wirkt und so sicherstellt, dass das Problem wohldefiniert bleibt.
All dies folgt nicht aus der Unschärfenrelation. Diese kodiert lediglich eine systemunabhängie geometrische Struktur eines beliebigen Hilbertraumes, während die Frage der Lokalisierung, der zulässigen Energien usw. direkt von der spezifischen Form des Hamiltonoperators abhängt. Wenn man beim Wasserstoffatom ausschließlich mittels der Unschärfenrelation argumentiert, setzt man implizit die Ergebnisse dieser Betrachtungen voraus; das ist m.E. unzulässig.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TAppel
Anmeldungsdatum: 21.02.2016
Beiträge: 13
|
 TAppel Verfasst am: 03. März 2016 15:27 Titel: TAppel Verfasst am: 03. März 2016 15:27 Titel: |
 |
|
Kannst du (jemand) mir villt. nen Link oder Buchnamen geben, wo solche Sachen (Schrödingergleichung...) von den Grundlagen aus erläutert werden (Deutsch/Englisch)? :3
LG
_________________
Wichtig ist, dass wie niemals aufhören zu fragen." -Albert Einstein |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
 TomS Verfasst am: 04. März 2016 01:09 Titel: TomS Verfasst am: 04. März 2016 01:09 Titel: |
 |
|
Welchen Anspruch hast du denn bzgl. mathematischer / formaler Fundierung?
Ich schätze den "Sakurai" sehr. Sehr gelobt wird auch der "Ballantine", den habe ich jedoch immer nur überflogen. Einen Link kann ich dir nicht empfehlen.
Am besten, du schaust dir mal verschiedene Bücher in der Bibliothek an.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|
















 - trotzdem Danke, die Grundzüge kapier ich.
- trotzdem Danke, die Grundzüge kapier ich.