| Autor |
Nachricht |
Otter
Gast
|
 Otter Verfasst am: 31. Jul 2015 10:35 Titel: Unschärferelation: Aussage? Otter Verfasst am: 31. Jul 2015 10:35 Titel: Unschärferelation: Aussage? |
 |
|
Moin,
auf der Wikipedia heißt es:
| Zitat: | | Es ist prinzipiell unmöglich, den Ort und den Impuls eines Teilchens gleichzeitig mit unbegrenzter Genauigkeit zu messen. |
de.wikipedia.org/wiki/Heisenbergsche_Unsch%C3%A4rferelation
Bei Popper heißt es:
| Zitat: | | Die Unbestimmtheitsrelationen beziehen sich ja nur auf die Zustandsgrößen, die dem Teilchen nach der Messung zukommen; Ort und Impuls eines Elektrons bis zum Augenblick der Messung kann man ohne grundsätzliche Genauigkeitsbeschränkungen feststellen. |
Logik der Forschung (2002), S. 170.
Das heißt also: ich kann durch eine Messung den exakten Ort und Impuls eines Teilchens bestimmen. Da meine Messung aber das Teilchen beeinflusst, kann ich über den Zustand des Teilchens nach der Messung keine exakten Angaben mehr machen, oder? Widersprechen sich die zitierten Aussagen nicht?
Danke für Hinweise. |
|
 |
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
 bassiks Verfasst am: 31. Jul 2015 10:52 Titel: bassiks Verfasst am: 31. Jul 2015 10:52 Titel: |
 |
|
| Zitat: | | Ort und Impuls eines Elektrons bis zum Augenblick der Messung kann man ohne grundsätzliche Genauigkeitsbeschränkungen feststellen. |
Das hängt jetzt ein bisschen davon ab wie man die QM interpretiert und was man unter Ort und Impuls versteht. Die klassischen Eigenschaften eines Teilchens "Ort" und "Impuls" existieren den meisten Interpretationen folgend gar nicht bevor man eine Messung durchführt. Das Zitat für sich würde ich also eher als falsch bezeichnen. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8588
|
 jh8979 Verfasst am: 31. Jul 2015 11:16 Titel: jh8979 Verfasst am: 31. Jul 2015 11:16 Titel: |
 |
|
| bassiks hat Folgendes geschrieben: | | Das Zitat für sich würde ich also eher als falsch bezeichnen. |
Wieso "eher"? In der QM gibt es keine gleichzeitigen Eigenzustände für den Orts- und Impulsoperator. Daher ist die Aussage in der QM falsch. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 31. Jul 2015 11:36 Titel: TomS Verfasst am: 31. Jul 2015 11:36 Titel: |
 |
|
Ich müsste mal Poppers Buch aus dem Bücherschrank holen, aber zunächst mal sage ich, dass diese Aussage schlicht falsch ist!
Ignorieren wir mal ein paar mathematische Subtilitäten des Impulsoperators.
Für einem beliebigen Quantenzustand gilt, dass die Unschärfenrelation vor bzw. unabhängig von einer Messung erfüllt ist. Das ist letztlich eine mathematische Eigenschaft, die aus der Geometrie des Hilbertraumes und damit der Axiomatik der QM exakt und beweisbar folgt.
D.h. zum ersten ist die Aussage von Wikipedia falsch, dass sich die Unschärfenrelation auf die Messung bezieht. Sie bezieht sich auf einen mathematischen Zustand.
Zum zweiten ist Poppers Aussage bzgl. dieses mathematischen Zustandes falsch oder zumindest extreme unpräzise. Man kann evtl. einen Ortseigenzustand präparieren (und von diesem den Ort mathematisch exakt bestimmen). Dann ist jedoch für diesen so präparierten Zustand der Impuls maximal unscharf.
Zum dritten ist Poppers Aussage bzw. Unterscheidung zwischen "vor" und "nach der Messung" im mathematischen Sinne falsch. Es gibt schlichtweg keinen Hilbertraumzustand, für den Poppers Aussage richtig ware.
Bisher habe ich von Mathematik, Quantenzustand usw., noch nicht von Messung gesprochen. Die Unschärfenrelation in ihrer mathematischen Form sagt nichts über die Messung bzw. den Messprozess!
Es ist offensichtlich klar, dass z.B. der Ort nicht schärfer gemessen werden kann, als er vor der Messung vorliegt. Das bedeutet nun nicht, dass er im Zuge einer Messung nicht exakt präpariert werden kann, d.h. dass nach der Messung ein scharfen Ort vorliegt. Aber das ist erst das Resultat der Messung im Sinne einer Präparation. Und natürlich wird dadurch wiederum der Impuls maximal unscharf.
Nun zur Realität. Man könnte versucht sein, einem Quantenobjekt in der Realität einen präzisen Ort UND Impuls zuzuschreiben, und die Unschärfe desselben einem unzureichenden mathematischen Formalimus der QM anzulasten. Man kann jedoch mathematisch beweisen UND experimentell überprüfen, dass eine Vervollständigung der QM im Sinne von "verborgenen Variablen", die exakt scharf definierte Werte tragen, jedoch "verborgen" bleiben, der QM theoretisch und experimentell widerspricht (Bell, Aspect u.v.a.m.).
D.h. dass Poppers Aussage auch dann falsch ist, wenn er sie auf die "Realität" beziehen möchte.
Ich hätte gerne mal das Kapitel gewusst, in dem das stehen soll. Ich kann nicht glauben, dass Popper derat offensichtliche Fehler begangen hat.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Otter
Gast
|
 Otter Verfasst am: 31. Jul 2015 20:49 Titel: Otter Verfasst am: 31. Jul 2015 20:49 Titel: |
 |
|
Hallo und danke für die Antworten. Als Nichtphysiker verstehe ich zwar nur Fetzen davon, aber immerhin weiß ich jetzt mehr im Bezug auf das Buch  Das Problem mit dem Buch ist auch, dass es wohl über 50 Jahre lang verbessert wurde und zum Original immer wieder Verbesserungen, Zusätze und Korrekturen kamen. Einige Dinge hat Popper auch schlichtweg widerrufen. Meines Wissens aber diesen Absatz nicht, ich finde keine Sternchen oder etwas in den Fußnoten. Er findet sich in Kapitel IX, "Bemerkungen zur Quantenmechanik", Nummer 73. Das Problem mit dem Buch ist auch, dass es wohl über 50 Jahre lang verbessert wurde und zum Original immer wieder Verbesserungen, Zusätze und Korrekturen kamen. Einige Dinge hat Popper auch schlichtweg widerrufen. Meines Wissens aber diesen Absatz nicht, ich finde keine Sternchen oder etwas in den Fußnoten. Er findet sich in Kapitel IX, "Bemerkungen zur Quantenmechanik", Nummer 73. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 31. Jul 2015 21:29 Titel: Jayk Verfasst am: 31. Jul 2015 21:29 Titel: |
 |
|
Ehrlich gesagt, verstehe ich die Aussage gar nicht so richtig. Ich habe mich nicht so sehr mit Popper beschäftigt (ich weiß, sollte ich mal nachholen). Aber wenn man bedenkt, wann er das geschrieben hat, halte ich das, was bassiks geschrieben hat, für sehr passend (Kopenhagener Interpretation). Obwohl die Kopenhagener Interpretation aus meiner Sicht einen philosophischen Wert von =Null hat...
Aber ich habe mit der Aussage folgendes Problem: Wie kann ich etwas feststellen, ohne zu messen? Für mich sind das synonyme Begriffe (in der Kopenhagener Interpretation ist eine Messung "definiert" als Wechselwirkung eines Quantenobjekts mit einem klassischen Objekt, aber um eine "klassische" Eigenschaft "festzustellen", brauche ich wohl so etwas).
Klassisch interpretiert, machen der Erwartungswert und die Unschärfe einer Observable bzgl. eines Zustands doch vor der Messung eine Aussage über die Statistik der Meßwerte, die ich nach der Messung erhalten werde. |
|
 |
Gast2
Gast
|
 Gast2 Verfasst am: 01. Aug 2015 00:18 Titel: allgemeine Unschärferelation Gast2 Verfasst am: 01. Aug 2015 00:18 Titel: allgemeine Unschärferelation |
 |
|
Also, ganz allgemein kann man für zwei quantenmechanische Observablen die allgemeine Unschärferelation hinschreiben, wenn man die Observablen um ihren Erwartungswert zentriert und dann einmal die Cauchy-Schwarz-Ungleichung anwendet. Dann bekommt man die allgemeine Unschärferelation für z.B. zwei qm Observablen A, B, zu:
[latex] \Delta_\psi A \cdot \Delta_\psi B \geq \frac{1}{2}|E(i[A,B])| [/latex]
wobei E der Erwartungswert ist
[latex] E_\psi (A) = (\psi, A \psi) [/latex]
zu innerem Produkt (.,.). Verwendet man nun die quantenmechanischen Orts- bzw. Impulsoperatoren, definiert auf dem Schwartzraum (der dicht im Hilbertraum L^2 liegt), so erhält man daraus die als die Heisenberg'sche bekannte Orts-Impuls-Unschärfe.
Anders ausgedrückt: da Orts- und Impulsoperator einen nicht verschwindenen Kommutator [.,.] besitzen, haben beide keinen Satz simulataner Eigenfunktionen - sie sind nicht gleichzeitig beliebig genau messbar. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 01. Aug 2015 09:47 Titel: TomS Verfasst am: 01. Aug 2015 09:47 Titel: |
 |
|
| Gast2 hat Folgendes geschrieben: | Also, ganz allgemein kann man für zwei quantenmechanische Observablen die allgemeine Unschärferelation hinschreiben, wenn man die Observablen um ihren Erwartungswert zentriert und dann einmal die Cauchy-Schwarz-Ungleichung anwendet. Dann bekommt man die allgemeine Unschärferelation für z.B. zwei qm Observablen A, B, zu:
| )
wobei E der Erwartungswert ist
 = (\psi, A \psi) )
zu innerem Produkt (.,.). Verwendet man nun die quantenmechanischen Orts- bzw. Impulsoperatoren, definiert auf dem Schwartzraum (der dicht im Hilbertraum L^2 liegt), so erhält man daraus die als die Heisenberg'sche bekannte Orts-Impuls-Unschärfe.
Anders ausgedrückt: da Orts- und Impulsoperator einen nicht verschwindenen Kommutator [.,.] besitzen, haben beide keinen Satz simulataner Eigenfunktionen - sie sind nicht gleichzeitig beliebig genau messbar. |
So ist das.
Wir versuchen zu verstehen, was Popper dazu bringt, diese Fakten anders zu interpretieren.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 01. Aug 2015 09:53 Titel: TomS Verfasst am: 01. Aug 2015 09:53 Titel: |
 |
|
| Popper (Logik der Forschung) hat Folgendes geschrieben: | | Ort und Impuls eines Elektrons bis zum Augenblick der Messung kann man ohne grundsätzliche Genauigkeitsbeschränkungen feststellen. |
Was genau meint Popper mit "feststellen"?
"Messen" kann es nicht sein, denn es geht ja um den Zeitraum vor der Messung.
Und eine "Berechnung" kann es gemäß der QM auch nicht sein, denn wie oben gesagt, lässt die Hilbertraumgeometrie keine gemeinsamen Eigenzstände zu.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Günther
Anmeldungsdatum: 23.11.2010
Beiträge: 330
|
 Günther Verfasst am: 01. Aug 2015 18:25 Titel: Günther Verfasst am: 01. Aug 2015 18:25 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
D.h. zum ersten ist die Aussage von Wikipedia falsch, dass sich die Unschärfenrelation auf die Messung bezieht. Sie bezieht sich auf einen mathematischen Zustand.
|
Ist sie tatsächlich falsch? Folgt aus der Unschärferelation nicht, daß man Ort und Impuls nicht gleichzeitig beliebig genau messen kann? ?( |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 01. Aug 2015 22:48 Titel: TomS Verfasst am: 01. Aug 2015 22:48 Titel: |
 |
|
Aus der Formel folgt zunächst, dass es im (mathematischen) Formalismus der QM unmöglich ist, einen (mathematischen) Zustand zu konstruieren, für den Ort und Impuls gleichzeitig beliebig genau definiert sind. Das noch hat nichts mit einer Messung zu tun.
Glaubt man nun, dass der mathematische Zustand die Realität repräsentiert, so bedeutet das, dass für das reale Objekt ebenfalls Ort und Impuls nicht gleichzeitig beliebig genau existieren. Damit können sie natürlich auch nicht gleichzeitig beliebig genau gemessen werden.
Trotzdem ist der argumentative Weg von der Formel zur Messung sehr weit ...
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Günther
Anmeldungsdatum: 23.11.2010
Beiträge: 330
|
 Günther Verfasst am: 02. Aug 2015 09:47 Titel: Günther Verfasst am: 02. Aug 2015 09:47 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Damit können sie natürlich auch nicht gleichzeitig beliebig genau gemessen werden.
|
Und das ist die Aussage dieses Wikipedia Zitats, was sollte daran falsch sein? Vielleicht vermißt du den Kontext:
| Zitat: | Unter dem Begriff des Unschärfe- oder auch Unbestimmtheitsprinzips werden die folgenden Aussagen zusammengefasst, die zwar miteinander verwandt sind, jedoch physikalisch unterschiedliche Bedeutung haben.[4] Sie sind hier beispielhaft für das Paar Ort und Impuls notiert.
1.Es ist nicht möglich, einen quantenmechanischen Zustand zu präparieren, bei dem der Ort und der Impuls beliebig genau definiert sind.
2.Es ist prinzipiell unmöglich, den Ort und den Impuls eines Teilchens gleichzeitig mit unbegrenzter Genauigkeit zu messen.
3.Die Messung des Impulses eines Teilchens ist zwangsläufig mit einer Störung seines Ortes verbunden, und umgekehrt.
Jede dieser drei Aussagen lässt sich quantitativ in Form sogenannter Unschärfe-Relationen formulieren, die eine untere Grenze für die erreichbare minimale Unschärfe der Präparation bzw. Messung angeben.
|
Es ist bekannt, daß Wikipedia gelegentlich ungenaue oder sogar falsche Aussagen enthält. Deshalb interessiert mich, wie sich das im hier diskutierten Fall verhält. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 02. Aug 2015 14:31 Titel: TomS Verfasst am: 02. Aug 2015 14:31 Titel: |
 |
|
| Günther hat Folgendes geschrieben: | | TomS hat Folgendes geschrieben: | Damit können sie natürlich auch nicht gleichzeitig beliebig genau gemessen werden.
|
Und das ist die Aussage dieses Wikipedia Zitats, was sollte daran falsch sein? |
Es geht darum, was primär ist.
Wenn in einem Krug kein Bier enthalten ist, kann man auch keines daraus trinken.
| Günther hat Folgendes geschrieben: | | Vielleicht vermißt du den Kontext ... |
Ich kenne den Kontext, und ich halte ihn für massiv irreführend.
| Zitat: | | Unter dem Begriff des Unschärfe- oder auch Unbestimmtheitsprinzips werden die folgenden Aussagen zusammengefasst, die zwar miteinander verwandt sind, jedoch physikalisch unterschiedliche Bedeutung haben.[4] |
Ja, man fasst - ohne Not - Aussagen zusammen, die unterschiedliche Bedeutung haben. Das halte ich für unsauber.
| Zitat: | 1) Es ist nicht möglich, einen quantenmechanischen Zustand zu präparieren, bei dem der Ort und der Impuls beliebig genau definiert sind.
2) Es ist prinzipiell unmöglich, den Ort und den Impuls eines Teilchens gleichzeitig mit unbegrenzter Genauigkeit zu messen.
3) Die Messung des Impulses eines Teilchens ist zwangsläufig mit einer Störung seines Ortes verbunden, und umgekehrt. |
(1) sagt entweder etwas über das Unvermögen des Experimentalphysikers, einen Zustand zu präparieren, oder etwas über eine prinzipielle Unmöglichkeit (dass du nicht schneller als mit Lichtgeschwindigkeit fliegen kannst, hat nichts damit zu tun, dass du zu dumm bist, einen entsprechenden Antrieb zu bauen). In der QM geht es um die prinzipielle Unmöglichkeit, aus der die Unmöglichkeit der Präparation folgt.
(2) sagt wiederum entweder etwas über das Unvermögen des Experimentalphysikers, eine exakte Messung durchzuführen, oder etwas über eine prinzipielle Unmöglichkeit. Wiederum geht es um die prinzipielle Unmöglichkeit, aus der die Unmöglichkeit der Messung folgt.
(3) ist eine triviale Aussage.
Insgs. erfasst keine dieser drei Aussagen den Kern der quantenmechanischen Unschärfe, nämlich den einer prinzipiellen Unschärfe als direkte Konsequenz der Struktur der QM. Stattdessen stehen bei der Wikipedia die Schlussfolgerungen im Vordergrund.
| Zitat: | | Jede dieser drei Aussagen lässt sich quantitativ in Form sogenannter Unschärfe-Relationen formulieren, die eine untere Grenze für die erreichbare minimale Unschärfe der Präparation bzw. Messung angeben. |
dito
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 02. Aug 2015 14:44 Titel: TomS Verfasst am: 02. Aug 2015 14:44 Titel: |
 |
|
Die englische Wikipedia ist da wieder mal deutlich präziser unterwegs:
| Zitat: | In quantum mechanics, the uncertainty principle ... is any of a variety of mathematical inequalities asserting a fundamental limit to the precision with which certain pairs of physical properties of a particle ... can be "known" simultaneously ... The formal inequality relating the standard deviation of position and the standard deviation of momentum was derived by Earle Hesse Kennard later that year and by Hermann Weyl in 1928:

Historically, the uncertainty principle has been confused with a somewhat similar effect in physics, called the observer effect, which notes that measurements of certain systems cannot be made without affecting the systems. Heisenberg offered such an observer effect at the quantum level as a physical "explanation" of quantum uncertainty. It has since become clear, however, that the uncertainty principle is inherent in the properties of all [quantum mechnical systems] ... Thus, the uncertainty principle actually states a fundamental property of quantum systems, and is not a statement about the observational success of current technology. |
|
|
 |
Günther
Anmeldungsdatum: 23.11.2010
Beiträge: 330
|
 Günther Verfasst am: 02. Aug 2015 16:34 Titel: Günther Verfasst am: 02. Aug 2015 16:34 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Insgs. erfasst keine dieser drei Aussagen den Kern der quantenmechanischen Unschärfe, nämlich den einer prinzipiellen Unschärfe als direkte Konsequenz der Struktur der QM. Stattdessen stehen bei der Wikipedia die Schlussfolgerungen im Vordergrund.
|
Ja, kann ich jetzt nachvollziehen, danke. Bei der englischen Wikipedia tauch der Begriff Messung gar nicht erst auf, stattdessen ... limit to ... can be "known" simultaneously. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 02. Aug 2015 16:43 Titel: TomS Verfasst am: 02. Aug 2015 16:43 Titel: |
 |
|
Genau!
Angesichts der Tatsache, dass der Begriff "Messung" in allen Interpretationen (außer der von Everett) unklar bleibt bzw. nicht wirklich definiert ist, ist es schon seltsam, dass man die Unschärfenrelation gerade anhand der Messung einführen möchte. |
|
 |
semmelrot
Gast
|
 semmelrot Verfasst am: 03. Aug 2015 09:31 Titel: semmelrot Verfasst am: 03. Aug 2015 09:31 Titel: |
 |
|
@Tom.s
Du hast richtig erkannt, dass die Unschärferelation eine prinzipielle Unmöglichkeit darstellt und nicht mit dem Unvermögen des Experimentators hinsichtlich der Durchführung einer exakten Messung zu tun hat. Was dieses Prinzip sein soll , hast Du folgendes geschrieben
-....... lässt die Hilbertraumgeometrie keine gemeinsamen Eigenzstände zu.
-nämlich den einer prinzipiellen Unschärfe als direkte Konsequenz der Struktur der QM.
Kannst Du genauer erklären was Du mit
-Hilbertraumgeometrie
-Struktur der QM
meinst und wie daraus eine Unschärfe resultiert?Denn ich habe den Eindruck, dass Du dich hierbei gewaltig irrst. |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 03. Aug 2015 10:33 Titel: Ich Verfasst am: 03. Aug 2015 10:33 Titel: |
 |
|
Hi Tom,
jetzt hast du ihn auch an der Backe...
 |
|
 |
Otter
Gast
|
 Otter Verfasst am: 03. Aug 2015 11:09 Titel: Otter Verfasst am: 03. Aug 2015 11:09 Titel: |
 |
|
Hallo,
wenn das auf der Wikipedia falsch bzw. irreführend dargestellt ist, würde es mich sehr freuen, wenn einer der Experten hier dort eine kurze Anmerkung dazu macht, etwa in der Diskussion, oder einen Baustein für Qualitätssicherung einträgt. Kann das jemand übernehmen? Ich würde es machen, aber mein Fachwissen wäre zur Begründung der ganzen Sache nicht ausreichend...
Danke! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 03. Aug 2015 11:41 Titel: TomS Verfasst am: 03. Aug 2015 11:41 Titel: |
 |
|
| semmelrot hat Folgendes geschrieben: | Kannst Du genauer erklären was Du mit
-Struktur der QM
-Hilbertraumgeometrie
meinst und wie daraus eine Unschärfe resultiert? |
Die Struktur der QM wird durch ihre Axiome definiert. Wir benötigen für die Unschärfenrelation lediglich folgende
1) Der Zustandsraum eines quantenmechanischen Systems wird durch einen separablen Hilbertraum H repräsentiert.
2) Die Observablen eines quantenmechanischen Systems werden durch selbst-adjungierte Operatoren A auf H repräsentiert.
3) Ein Zustand eines quantenmechanischen Systems, in dem eine Observablen einen scharfen Wert a hat, wird durch einen Eigenzustand |a> des entsprechenden Operators A beschrieben sein.
Aus dieser Struktur folgt die Unschärfenrelation als beweisbares mathematisches Theorem:
https://en.wikipedia.org/wiki/Uncertainty_principle#Robertson.E2.80.93Schr.C3.B6dinger_uncertainty_relations
Der Beweis verwendet die Cauchy–Schwarz-Ungleichung
https://en.wikipedia.org/wiki/Cauchy%E2%80%93Schwarz_inequality
die aus der Geometrie des Hilbertraumes (Vektoren, Skalarprodukt, daraus induzierte Norm) folgt.
Für das Produkt der Unschärfen σ zweier Observablen A, B gilt allgemein

d.h. dass für zwei nicht-vertauschende Observablen

das Produkt ihrer Unschärfen im Allgemeinen nicht Null sein kann.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 03. Aug 2015 11:50, insgesamt einmal bearbeitet |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 03. Aug 2015 11:50 Titel: TomS Verfasst am: 03. Aug 2015 11:50 Titel: |
 |
|
| Otter hat Folgendes geschrieben: | Hallo,
wenn das auf der Wikipedia falsch bzw. irreführend dargestellt ist, würde es mich sehr freuen, wenn einer der Experten hier dort eine kurze Anmerkung dazu macht, etwa in der Diskussion, oder einen Baustein für Qualitätssicherung einträgt. Kann das jemand übernehmen? Ich würde es machen, aber mein Fachwissen wäre zur Begründung der ganzen Sache nicht ausreichend...
Danke! |
Ich kann das gerne machen, aber nach meinem Urlaub.
Meine Erfahrung sagt mir jedoch, dass die sogenannten "Experten" bei Wikipedia derartige Darstellungen nicht "mögen". Ich habe das schonmal bei der Diskussion der Hawkimgstrahlung feststellen müssen:
https://de.wikipedia.org/wiki/Diskussion:Hawking-Strahlung#Der_Begriff_.22virtuelle_Teilchen.22_ist_diesem_Kontext_falsch.21
Ansonsten könntest du das mit dem Hinweis auf die ernglische Wikipedia selbst durchführen. Diese setzt den Formalismus der QM als primär an, geht dann davon aus, dass dieser Formalismus universell gültig ist, und leitert daraus wiederum die universelle Gültigkeit der Unschärfernrelation ab, in dem Sinne, dass zwei nicht-vertauschenden Observablen i.A. nicht gleichzeitig ein scharfer Wert zukommen kann.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18557
|
 TomS Verfasst am: 03. Aug 2015 11:58 Titel: TomS Verfasst am: 03. Aug 2015 11:58 Titel: |
 |
|
Wichtig: es gibt durchaus Spezialfälle, für die das Produkt der Unschärfen auch für nicht-vertauschende Observablen exakt Null ist.
Bsp.: wir betrachten ein System mit den Eigenzuständen


zum Operator
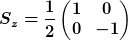

Die Spinoperatoren erfüllen für k = 1,2,3 (entspr. x,y,z) die Algebra
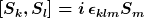
Für das Produkt der Unschärfen von Spin-x und Spin-y folgt:

D.h. die Unschärfe verschwindet genau dann, wenn der Erwartungswert für die z-Komponente verschwindet. Derartige Zustände kann man jedoch leicht aus den Eigenzuständen konstruieren:
)
)

Dies ist auch nicht weiter verwunderlich, denn in diesem Zustand verschwindet gerade die Streuung der x-Komponente

da es sich um einen Eigenzustand der x-Komponente handelt:



d.h.
})
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Resipisco
Gast
|
 Resipisco Verfasst am: 06. Aug 2015 12:14 Titel: Der formale Geist verliert die natürlich Denkenden! Resipisco Verfasst am: 06. Aug 2015 12:14 Titel: Der formale Geist verliert die natürlich Denkenden! |
 |
|
Ich finde Eure Diskussion spannend aber auch enttäuschend.
Leiter haben Mathematiker die unangenehme Eigenschaft alle nicht Mathematiker durch die komlexe formale Ausdrucksweise vom Verständnis der Diskussion auszuschließen.
Versucht doch mal die Dinge im natürlicher Sprache verständlich auszudrücken. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 06. Aug 2015 15:03 Titel: Jayk Verfasst am: 06. Aug 2015 15:03 Titel: |
 |
|
@Resipisco: Wenn Du eine nicht ganz so abstrakte Darstellung der QM suchst, empfehle ich den Landau/Lifschitz 3. Der enthält allerdings stark die Handschrift einer ganz bestimmten Interpretation, nämlich der Kopenhagener Interpretation.
Letztlich mußt Du Dir klarmachen, was ein Zustand ist: Eine tote Katze ist einer, eine lebendige Katze ist einer, aber auch eine halbtote Katze ist einer (halbtot heißt nicht, daß sie zappelt, nachdem sie vom Auto überfahren wurde, sondern daß sie gleichzeitig tot und lebendig ist). Man kann Zustände immer superponieren! Etwas weniger esoterisch: ein Teilchen mit einem bestimmten Impuls (ebene Welle) ist einer, ein Teilchen mit einem anderen ist einer, aber auch ein Teilchen mit zwei Impulsen gleichzeitig ist einer. Entscheidend ist, daß bei einer Messung im allgemeinen Zustände verändert werden (dies drückt sich dadurch aus, daß Observablen in der QM durch Operatoren dargestellt werden). Der Zustand kann geschrieben werden als Überlagerung eines Teils, der bei der Messung verändert wird, und eines Teils, der nicht verändert wird, und nach der Messung bleibt immer nur der unveränderliche Teil übrig oder auch nur ein Teil davon (eine Messung eines bestimmten Wertebereichs entspricht einer Projektion des Zustands auf einen Unterraum des Zustandsraums, dem so genannten Kollaps der Wellenfunktion – warum: darüber wird wild spekuliert).
Welcher Anteil nach der Messung übrig bleibt, hängt davon ab, welche Observable gemessen wird. Auch die Reihenfolge spielt im allgemeinen eine Rolle (versuche mal, einen Strich in der Ebene nacheinander auf zwei nicht zueinander senkrechte Geraden zu projizieren – das Ergebnis wird davon abhängen, in welcher Reihenfolge du vorgehst!). Und die allgemeine Unschärferelation besagt, daß man für jeden Zustand, für den die Reihenfolge eine Rolle spielt, eine minimale Unschärfe ableiten kann (das Wort "Unschärfe" kommt von der probabilistischen Deutung: Wenn Du einen Zustand 60% Impuls 1 + 40% Impuls 2 so deutest, daß in 40% der Fälle Impuls 2 vorliegt, dann wirst Du eine nicht verschwindende Standardabweichung ausrechnen, d.h. der Zustand 60%...+40%... hat eine Unschärfe bzgl. der Observablen Impuls, und die Unschärferelation besagt, daß das Produkt der Unschärfen dieses Zustands bzgl. der beiden Observablen einen minimalen Wert hat, der proportional dazu ist, wie groß der Unterschied der beiden Projektionsvorgänge ist).
Die Frage ist natürlich, was eine Projektion anschaulich bedeutet. Dafür braucht man ja ein Verständnis davon, was senkrecht bedeutet (-> eine Hilbertraumgeometrie). Die Idee ist, daß man in der QM immer fragen kann, wie viel eines Zustands 1 in einem anderen Zustand 2 enthalten ist (es gibt also ein so genanntes Skalarprodukt und das bedeutet im Wesentlichen das Axiom, daß Zustände durch Vektoren in einem Hilbertraum beschrieben werden). Zwei Zustände sind senkrecht zueinander, wenn sie jeweils nichts des anderen Zustands enthalten.
Übrigens: "Es ist nicht möglich, ... gleichzeitig mit unbegrenzter Genauigkeit zu messen" halte ich für eine sehr problematische Beschreibung der Unschärferelation. Man kann immer nur eine Observable auf einmal messen (prinzipiell, also auch bei kommutierenden Observablen). |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 07. Aug 2015 13:48 Titel: index_razor Verfasst am: 07. Aug 2015 13:48 Titel: |
 |
|
| Jayk hat Folgendes geschrieben: | (eine Messung eines bestimmten Wertebereichs entspricht einer Projektion des Zustands auf einen Unterraum des Zustandsraums, dem so genannten Kollaps der Wellenfunktion – warum: darüber wird wild spekuliert).
|
Diese Behauptung finde ich unhaltbar. Zu den in Teilchendetektoren gemessenen Observablen gehören unter anderem Energie und Impuls der Streuprodukte. In keinem der Fälle befindet sich nach meinem Verständnis das Teilchen nach der Messung in einem Eigenzustand zum Wert der gemessenen Observablen.
Der Impuls von massiven, geladenen Teilchen wird aus den Spuren in Driftkammern o.ä. rekonstruiert. Dazu werden in einem EM-Feld sukzessive Ortsmessungen vorgenommen und mit Informationen über Ladung kombiniert, um aus der Bahnkrümmung auf den Impuls zu schließen. Handelte es sich dabei um ideale Ortsmessungen und würde es stimmen, daß eine solche auf Ortseigenzustände projiziert, wäre ja bereits nach der ersten Messung die gesamte Information über den Impuls vollständig zerstört. Zwar sind die Meßgenauigkeiten in diesem Fall viel geringer als die Impuls- und Ortsunschärfe. Trotzdem erkennt man m.E. ein prinzipielles Problem des Projektionsaxioms: Denn es werden hier eindeutig Ort und Impuls der Teilchen gemessen. Die zugehörigen Projektionen ergeben aber auch bei Berücksichtigung der jeweiligen Meßungenauigkeiten im allgemeinen unterschiedliche Zustände. Das erkennt man schon daran, daß der initiale Zustand gleichzeitig beliebig breite Orts- und Impulsverteilungen aufweisen könnte (Die Unschärferelation liefert ja nur eine Untergrenze). Auf welchen Unterraum müßte man nun projizieren? Wenn man dieses Verfahren als geeignet zur Impulsmessung ansieht, muß man, denke ich, akzeptieren, daß es dem Projektionsaxiom widerspricht, denn die Messung ist erst abgeschlossen, nachdem man weiß, wie stark der anfängliche Impuls des Teilchens in dem angelegten Feld abgelenkt wird. Es kann also hinterher (hinreichende Meßgenauigkeit vorausgesetzt) kein Eigenzustand mit dem gemessenen Impuls vorgelegen haben. (Von der problematischen Frage, wann genau nun "unmittelbar nach der Messung" sein soll, mal ganz zu schweigen. Die Vagheit in dieser Formulierung birgt jedoch das Potential das Projektionsaxiom gegen jegliche Gegenbeispiele zu immunisieren. Wie soll man zeigen, daß ein Zustand "unmittelbar genug" nach einer Messung vorgelegen hat?)
Noch deutlicher ist das m.E. bei Energiemessungen: Photonenenergien werden in elektromagnetischen Kalorimetern gemessen, indem die Photonen ihre Energie an das Kalorimetermedium abgeben. Nach gängiger Vorstellung wird dabei vermittels Paarerzeugung und Bremsstrahlung ein Teilchenschauer erzeugt. Die initialen Photonen werden also dabei im Medium absorbiert. Sie sind demzufolge auch nicht in einem Eigenzustand der zuvor gemessenen Energie, sondern weg. Allgemein wird, denke ich, die Energie von Teilchen gemessen, indem diese Energie vollständig an ein Medium abgegeben wird, deren "Kraftwirkung", d.h. dE/dx, auf die fraglichen Teilchen bekannt ist. Was auch immer dabei mit ihnen im Detail passiert, sie haben hinterher schon aus Gründen der Energieerhaltung auf keinen Fall die Energie, die das Kalorimeter an ihnen gemessen hat.
Die Durchführung und Interpretation dieser Messungen beruht nicht auf irgendeiner axiomatisch zementierten Gewißheit über den Zustand nach der Messung, sondern auf der Kenntnis des Verhaltens der zu vermessenden Teilchen innerhalb des Detektors während der Messung, also m.a.W. darauf, daß man genau über dieses "was auch immer dabei passiert" einigermaßen konkrete Vorstellungen hat. Man hätte keine Möglichkeit irgendwas zu messen, ohne Kenntnis über die Wechselwirkungen zwischen dem (mutmaßlichen) Meßgerät und Meßobjekt. (Woher würde man sonst überhaupt wissen, daß ein konkretes physikalisches System, wie eine Ansammlung von Drähten in einer gasgefüllten Kammer, ein Meßgerät zur Bestimmung der Observable "Ort" eines anderen physikalischen Systems ist?) Diese Kenntnis nützt einem nur insofern etwas, als das Gesamtsystem zumindest prinzipiell bekannten Bewegungsgesetzen folgt, was im Falle der Quantenmechanik heißt: der Schrödingergleichung. ("Prinzipiell", weil es natürlich erlaubt bleibt gerade für makroskopische Meßapparate notwendige Näherungen zu verwenden.) Wenn jede Messung durch so eine Wechselwirkung beschrieben werden muß, ist es unmöglich, daß sie gleichzeitig der Wirkung eines Projektionsoperators entspricht, denn die quantenmechanische Zeitentwicklung muß unitär sein. Der Kern der Kollapsinterpretation ist also, daß eine Messung entweder etwas prinzipiell völlig anderes ist, als eine quantenmechanische Wechselwirkung zwischen Meßgerät und Meßobjekt oder -- noch schlimmer -- sie widerspricht der Interpretation des Zustands als Wahrscheinlichkeitsamplitude.
Das Meßproblem besteht m.E. eigentlich auch nicht in der Frage, wie, warum oder wann der Kollaps des Zustandes stattfindet. Dieser Kollaps scheint mir, wie gesagt, sowieso mehr oder weniger ein Theoretikermythos zu sein. Der Messung ist eigentlich egal, in welchem Zustand sich das System hinterher befindet und im Prinzip ist alles möglich was mit den Grundeigenschaften quantenmechanischer Zeitentwicklung verträglich ist. Das eigentliche Problem besteht darin, wie sich aus dem anfänglichen Zustand ein konkreter Meßwert ergibt. Antworten, die den Kollaps schon voraussetzen, erzeugen m.E. mehr Probleme, als sie lösen, indem sie viel zu brachial in die Struktur der Quantenmechanik eingreifen. Ich zumindest finde die Implikation, daß Messungen prinzipiell nicht über fundamentale Wechselwirkungen beschreibbar sein sollten, völlig unakzeptabel. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 07. Aug 2015 21:48 Titel: Jayk Verfasst am: 07. Aug 2015 21:48 Titel: |
 |
|
Wow, ausgerechnet an dieser Stelle hatte ich keinen Widerspruch erwartet...
| index_razor hat Folgendes geschrieben: | | Ich zumindest finde die Implikation, daß Messungen prinzipiell nicht über fundamentale Wechselwirkungen beschreibbar sein sollten, völlig unakzeptabel. |
Ich auch.
Aber verläßt Du damit nicht die Standard-QM? (also auf Basis der Postulate...)
In den Postulaten taucht der Meßprozeß auf. Und dort ist auch immer nur eine Messung auf einmal vorgesehen. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Aug 2015 10:42 Titel: index_razor Verfasst am: 08. Aug 2015 10:42 Titel: |
 |
|
| Jayk hat Folgendes geschrieben: | Wow, ausgerechnet an dieser Stelle hatte ich keinen Widerspruch erwartet...
| index_razor hat Folgendes geschrieben: | | Ich zumindest finde die Implikation, daß Messungen prinzipiell nicht über fundamentale Wechselwirkungen beschreibbar sein sollten, völlig unakzeptabel. |
Ich auch.
Aber verläßt Du damit nicht die Standard-QM? (also auf Basis der Postulate...)
In den Postulaten taucht der Meßprozeß auf. Und dort ist auch immer nur eine Messung auf einmal vorgesehen. |
Ich finde die Formulierung adäquat, daß bei einer Messung die möglichen Meßwerte aus dem Spektrum eines hermiteschen Operators stammen und daß die Wahrscheinlichkeit für das Auftreten des Meßwertes  im Zustand im Zustand 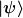 , die Amplitude , die Amplitude  hat, wobei hat, wobei  der (möglicherweise uneigentliche) Eigenvektor zu der (möglicherweise uneigentliche) Eigenvektor zu  ist. Das besagt nichts über den Zustand nach der Messung, sondern nur über das mögliche Ergebnis der Messung in Form des auftretenden Meßwertes. Es spielt auch in dieser Formulierung gar keine Rolle, wie verschiedene Messungen zeitlich zueinander in Beziehung stehen, insbesondere sehe ich auch keine Probleme darin, eine Impulsmessung an ist. Das besagt nichts über den Zustand nach der Messung, sondern nur über das mögliche Ergebnis der Messung in Form des auftretenden Meßwertes. Es spielt auch in dieser Formulierung gar keine Rolle, wie verschiedene Messungen zeitlich zueinander in Beziehung stehen, insbesondere sehe ich auch keine Probleme darin, eine Impulsmessung an 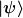 aus einer Folge von Ortsmessungen an demselben Zustand bestehen zu lassen. aus einer Folge von Ortsmessungen an demselben Zustand bestehen zu lassen.
Ich halte die Interpretation des quantenmechanischen Zustands als Wahrscheinlichkeitsamplituden und die sich daraus ergebenden Forderungen an die Zeitentwicklung für wesentlicher für die Quantenmechanik, als die Festlegung welcher Zustand nach einer Messung vorzuliegen hat. Genauer gesagt halte ich eine derartige Festlegung für vollkommen überflüssig. Wegen der Schwierigkeiten, die ich insbesondere bei dem Projektionspostulat sehe, bin ich auch der Ansicht, daß es nicht zur Standardformulierung der Quantenmechanik gehört (oder gehören sollte). |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 08. Aug 2015 13:14 Titel: Jayk Verfasst am: 08. Aug 2015 13:14 Titel: |
 |
|
Hm, okay. Ich bin auch kein Freund der Postulate (ich finde es auch grundsätzlich fragwürdig, Physik axiomatisieren zu wollen). Und wenn man eines Tages vielleicht verstanden hat, was wirklich beim Meßprozeß vorgeht, wird man sicher andere Postulate suchen müssen.
Aber ich habe ein Problem:
| index_razor hat Folgendes geschrieben: | | Ich halte die Interpretation des quantenmechanischen Zustands als Wahrscheinlichkeitsamplituden und die sich daraus ergebenden Forderungen an die Zeitentwicklung für wesentlicher für die Quantenmechanik, als die Festlegung welcher Zustand nach einer Messung vorzuliegen hat. |
Okay. Aber wenn ich eine Messung mache und fordere, "unmittelbar danach" keinen damit unvereinbaren Meßwert zu messen, folgt dann nicht aus der Wahrscheinlichkeitsinterpretation, daß es einen Kollaps gibt? Andernfalls würde das heißen, es gibt Meßwerte, die zwar nach Wahrscheinlichkeitsinterpretation vorkommen sollten, aber nicht vorkommen dürfen.
Und wenn man auf dieses Postulat verzichtet, kann ich mir nicht vorstellen, wie man der Unschärferelation eine anschauliche Bedeutung geben will. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 09. Aug 2015 15:45 Titel: index_razor Verfasst am: 09. Aug 2015 15:45 Titel: |
 |
|
| Jayk hat Folgendes geschrieben: |
Aber ich habe ein Problem:
| index_razor hat Folgendes geschrieben: | | Ich halte die Interpretation des quantenmechanischen Zustands als Wahrscheinlichkeitsamplituden und die sich daraus ergebenden Forderungen an die Zeitentwicklung für wesentlicher für die Quantenmechanik, als die Festlegung welcher Zustand nach einer Messung vorzuliegen hat. |
Okay. Aber wenn ich eine Messung mache und fordere, "unmittelbar danach" keinen damit unvereinbaren Meßwert zu messen, folgt dann nicht aus der Wahrscheinlichkeitsinterpretation, daß es einen Kollaps gibt?
|
Warum? Ich glaube das hängt davon ab, was während der Messung mit dem System passiert. Wenn die zu vermessende Observable durch die erste Messung nicht verändert wird, ist die Übergangsamplitude für ein anderes Ergebnis bei der zweiten Messung null, auch ohne Kollaps.
Nehmen wir an, wir haben ein System im Zustand 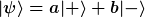 und zwei identische Meßapparate die nacheinander den Spin +/- messen. Die Indikatorvariable der Meßgeräte sei eine Observable mit Eigenwerten N, P, M für Null, Plus und Minus. Der Anfängliche Zustand des Meßaufbaus sei und zwei identische Meßapparate die nacheinander den Spin +/- messen. Die Indikatorvariable der Meßgeräte sei eine Observable mit Eigenwerten N, P, M für Null, Plus und Minus. Der Anfängliche Zustand des Meßaufbaus sei  . (Ich ignoriere weitere innere Freiheitsgrade der Meßgeräte, da ich glaube, daß sie keine Rolle spielen, aber die Formel komplizierter machen.) . (Ich ignoriere weitere innere Freiheitsgrade der Meßgeräte, da ich glaube, daß sie keine Rolle spielen, aber die Formel komplizierter machen.)
Die beiden Messungen finden nacheinander statt. Es existiert keine Wechselwirkung zwischen den beiden Meßgeräten, also weder reißt die erste Messung den zweiten Apparat aus seinem stand-by-Modus, noch ändert die zweite Messung nachträglich das Ergebnis der ersten. Dann ergibt sich nach der ersten Messung der Zustand
|N, 2\rangle)
und nach der zweiten Messung der Zustand

Es gibt keine Übergänge zu irgendeinem Zustand der Form 
für  . .
Wenn die erste Messung die gemessene Observable ändert, kommt bei der zweiten natürlich auch nicht mehr dasselbe raus. Beide Fälle erscheinen mir mit der Struktur der Quantenmechanik verträglich zu sein. Es ist falsch eine axiomatische Forderung zu erheben, die nur mit dem ersten Fall verträglich ist. Insbesondere wenn, wie ich glaube, der zweite der Normalfall ist.
| Zitat: |
Andernfalls würde das heißen, es gibt Meßwerte, die zwar nach Wahrscheinlichkeitsinterpretation vorkommen sollten, aber nicht vorkommen dürfen.
|
Was bei Folgemessungen vorkommen darf, bestimmt die Wechselwirkung zwischen System und Meßgerät während der ersten Messung, keine a-priori-Forderung.
| Zitat: |
Und wenn man auf dieses Postulat verzichtet, kann ich mir nicht vorstellen, wie man der Unschärferelation eine anschauliche Bedeutung geben will. |
Selbst wenn das stimmen würde, erscheinen mir die Probleme des Postulats zu schwerwiegend. Andererseits glaube ich, daß die Unschärferelation nicht direkt was mit der Frage zu tun hat, was bei einer Messung passiert, und erst recht keine Lösung des Meßproblems erfordert. Die Unschärferelation ist eine Aussage über die statistische Streuung von Meßwerten zweier Observabler in ein und demselben Zustand. Es ist mir nicht ersichtlich wie ein Postulat, welches fordert, daß nach der Messung einer dieser Observablen der Zustand auf die eine oder andere Weise geändert wird, die Aussage veranschaulichen soll. |
|
 |
|
|
















 Das Problem mit dem Buch ist auch, dass es wohl über 50 Jahre lang verbessert wurde und zum Original immer wieder Verbesserungen, Zusätze und Korrekturen kamen. Einige Dinge hat Popper auch schlichtweg widerrufen. Meines Wissens aber diesen Absatz nicht, ich finde keine Sternchen oder etwas in den Fußnoten. Er findet sich in Kapitel IX, "Bemerkungen zur Quantenmechanik", Nummer 73.
Das Problem mit dem Buch ist auch, dass es wohl über 50 Jahre lang verbessert wurde und zum Original immer wieder Verbesserungen, Zusätze und Korrekturen kamen. Einige Dinge hat Popper auch schlichtweg widerrufen. Meines Wissens aber diesen Absatz nicht, ich finde keine Sternchen oder etwas in den Fußnoten. Er findet sich in Kapitel IX, "Bemerkungen zur Quantenmechanik", Nummer 73.