| Autor |
Nachricht |
borromeus
Anmeldungsdatum: 29.12.2014
Beiträge: 509
|
 borromeus Verfasst am: 16. Feb 2016 20:32 Titel: Mathematische Axiome borromeus Verfasst am: 16. Feb 2016 20:32 Titel: Mathematische Axiome |
 |
|
Hat sich eigentlich schon wer auf diesem Planeten überlegt wie die Mathematik aussieht, wenn man "unsere" Grundaxiome nicht auf der Euklidischen Geometrie aufbaut sondern auf der Raumzeit?
Das muss ja dann alles irgendwie anders sein.... oder nicht?
|
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Feb 2016 20:41 Titel: index_razor Verfasst am: 16. Feb 2016 20:41 Titel: |
 |
|
|
Wie meinst du das? Was sind "unsere Grundaxiome"? Und wieso sollten sie ändern, wie die Mathematik aussieht? Die Mathematik kennt mehr als nur die euklidische Geometrie. Die Raumzeiten der relativistischen oder nichtrelativistischen Dynamik sind recht gut verstandene geometrische Strukturen (differenzierbare Mannigfaltigkeiten mit dieser oder jener Zusatzeigenschaft), die schon lange erfolgreich auf diesem Planeten studiert werden.
|
|
 |
borromeus
Anmeldungsdatum: 29.12.2014
Beiträge: 509
|
 borromeus Verfasst am: 16. Feb 2016 21:34 Titel: Re: Mathematische Axiome borromeus Verfasst am: 16. Feb 2016 21:34 Titel: Re: Mathematische Axiome |
 |
|
| Zitat: |
Das zentrale Objekt der riemannschen Geometrie ist die riemannsche Mannigfaltigkeit. Dies ist eine glatte Mannigfaltigkeit M zusammen mit einer Abbildung g, die in jedem Punkt p Element von M ein Skalarprodukt des Tangentialraums T_pM definiert, das heißt eine positiv definite, symmetrische Bilinearform.
|
Danke!
Ich sehe ein, da fehlt mir ein Studienabschluss, ich verstehe in diesem Satz 5 Wörter nicht, ich kenne sie nicht mal.
|
|
 |
borromeus
Anmeldungsdatum: 29.12.2014
Beiträge: 509
|
 borromeus Verfasst am: 16. Feb 2016 21:40 Titel: borromeus Verfasst am: 16. Feb 2016 21:40 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: | | Wie meinst du das? Was sind "unsere Grundaxiome"? Und wieso sollten sie ändern, wie die Mathematik aussieht? Die Mathematik kennt mehr als nur die euklidische Geometrie. Die Raumzeiten der relativistischen oder nichtrelativistischen Dynamik sind recht gut verstandene geometrische Strukturen (differenzierbare Mannigfaltigkeiten mit dieser oder jener Zusatzeigenschaft), die schon lange erfolgreich auf diesem Planeten studiert werden. |
Nun, unsere Mathematik baut doch auf ziemlich einfachen Grundaxiomen auf in der Euklidischen Geometrie.
Ich denke darum haben wir dann so seltsame Ausdrücke wie Wurzel aus 1 / (1 - v²/c²) nur weil Herr Anton an Frau Berta vorbeifährt und er wissen will wie lange ihr PKW ist.
Ich denke basierend auf einer Geometrie der Raumzeit könnte sich das ja einfacher darstellen... aber ich sehe schon, dass mir da vermutlich sämtliche Grundlagen fehlen um darüber nachzudenken.
Danke!
|
|
 |
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
 franz Verfasst am: 16. Feb 2016 22:24 Titel: franz Verfasst am: 16. Feb 2016 22:24 Titel: |
 |
|
|
Ich denke, daß die traditionelle menschliche Umwelt / Erfahrung quasi euklidisch ist und man das nach sehr langer und interessanter Beschäftigung auf das entsprechende Axiomensystem eingedampft hat, was man natürlich auch anders konstruieren könnte.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Feb 2016 22:42 Titel: index_razor Verfasst am: 16. Feb 2016 22:42 Titel: |
 |
|
| borromeus hat Folgendes geschrieben: |
Nun, unsere Mathematik baut doch auf ziemlich einfachen Grundaxiomen auf in der Euklidischen Geometrie.
Ich denke darum haben wir dann so seltsame Ausdrücke wie Wurzel aus 1 / (1 - v²/c²) nur weil Herr Anton an Frau Berta vorbeifährt und er wissen will wie lange ihr PKW ist.
Ich denke basierend auf einer Geometrie der Raumzeit könnte sich das ja einfacher darstellen...
|
Ja, du hast vollkommen recht. Die Raumzeit läßt sich geometrisch beschreiben und diese Geometrie ist verschieden von der euklidischen Geometrie, benötigt also andere Grundannahmen. Die Geometrie der relativistischen Raumzeit ist der euklidischen Geometrie verwandt, und wird auch als "pseudoeuklidisch" bezeichnet. Der prominenteste Unterschied ist, daß "Abstände" zwischen zwei verschiedenen Punkten nicht positiv sein müssen. Herr Anton und Frau Berta bewegen sich in verschiedene Richtungen innerhalb dieses pseudoeuklidischen Raumes, repräsentiert durch zwei Einheitsvektoren  und und 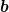 . Ein Skalarprodukt zwischen diesen beiden Vektoren gibt es auch, mit dessen Hilfe sich . Ein Skalarprodukt zwischen diesen beiden Vektoren gibt es auch, mit dessen Hilfe sich  tatsächlich auf die einfache Form tatsächlich auf die einfache Form  bringen läßt. Dies ergibt 1, sofern Anton und Berta in dieselbe "Raumzeitrichtung" fliegen, was in normaler Sprache bedeutet, daß sie relativ zueinander ruhen. Andernfalls ergibt es einen Wert größer als 1. (Was ein Unterschied zur euklidischen Geometrie ist, in der das Skalarprodukt am größten ist, wenn beide Vektoren in dieselbe Richtung zeigen.) bringen läßt. Dies ergibt 1, sofern Anton und Berta in dieselbe "Raumzeitrichtung" fliegen, was in normaler Sprache bedeutet, daß sie relativ zueinander ruhen. Andernfalls ergibt es einen Wert größer als 1. (Was ein Unterschied zur euklidischen Geometrie ist, in der das Skalarprodukt am größten ist, wenn beide Vektoren in dieselbe Richtung zeigen.)
Im allgemeinen benötigen Raumzeiten als Grundannahmen etwa folgendes: zunächst etwas, was man als "differenzierbare Struktur" bezeichnet. Das ist im wesentlichen die Existenz von Koordinatensystemen, mit deren Hilfe sich glatte Kurven und deren momentane "Geschwindigkeitsvektoren" (allerdings im Vierdimensionalen) definieren lassen. Desweiteren eine Vorschrift zur Parallelverschiebung, den sogenannten "affinen Zusammenhang", der angibt, was "geradlinig gleichförmig", "kräftefrei", etc. bedeutet, also neben der momentanen Geschwindigkeit auch sowas wie die Definition der "momentanen Beschleunigung" erlaubt. Er definiert auch, was "inertiale Bezugssysteme" und folglich was "Scheinkräfte" und dergleichen sind. Und schließlich irgendeine Möglichkeit der Zerlegung in disjunkte Schichten von "Momentaufnahmen". Diese Momentaufnahmen besitzen, sofern keine Gravitation vorliegt, euklidische Struktur und werden mit dem normalen "3-dimensionalen Raum der Anschauung" identifiziert. In der Relativitätstheorie definiert die pseudoeuklidische Metrik (das nichtpositive Abstandsmaß) sowohl den affinen Zusammenhang als auch die Raumzeitschichtung in Momentaufnahmen. Letztere ist allerdings im Gegensatz zur Newtonschen Raumzeit nur relativ zu einem Beobachter definiert. Jeder Beobachter teilt die Raumzeit also in verschiedene Schichten gleicher Zeit ein, was die bekannte Relativität der Gleichzeitigkeit zur Folge hat. In der Newtonschen Raumzeit hingegen gibt es eine absolute Zeit, d.h. die Raumzeit ist einfach eine Folge von absoluten euklidischen Räumen zu bestimmten absoluten Zeitpunkten.
|
|
 |
borromeus
Anmeldungsdatum: 29.12.2014
Beiträge: 509
|
 borromeus Verfasst am: 17. Feb 2016 00:02 Titel: borromeus Verfasst am: 17. Feb 2016 00:02 Titel: |
 |
|
Vielen lieben Dank!
Ich werde das vermutlich bei Lebzeiten nicht verstehen, aber ich versuche es mal, daher:
Fragen dazu:
Was ist glatt? glatte Kurven, glatte Mannigfaltigkeit?
Was sind "disjunkte Schichten"?
Bitte nochmal eine Erklärung zu "affiner Zusammenhang"!
Danke
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 18. Feb 2016 20:52 Titel: index_razor Verfasst am: 18. Feb 2016 20:52 Titel: |
 |
|
| borromeus hat Folgendes geschrieben: |
Fragen dazu:
Was ist glatt? glatte Kurven, glatte Mannigfaltigkeit?
|
Wie gesagt, ist das erste Problem, was wir innerhalb der Raumzeit lösen wollen, die momentane Geschwindigkeit eines Teilchens zu bestimmen. Wenn wir uns überhaupt vornehmen wollen, kinematische Sachverhalte innerhalb der Raumzeit darzustellen, müssen wir zumindest dazu in der Lage sein. In der elementaren Mechanik beschreibt man den momentanen Aufenthaltsort einfach durch einen Vektor ) , dessen Änderung durch Grenzwertbildung aus dem Differenzenquotienten, also durch die Ableitung , dessen Änderung durch Grenzwertbildung aus dem Differenzenquotienten, also durch die Ableitung
 - \vec{r}(t)}{\delta t})
berechnet wird. Als glatt kann ich diese Kurve bezeichnen, wenn dieser Grenzwert existiert. (Man fordert meist noch ein bißchen mehr, siehe unten.) Wenn er nicht existiert heißt das nämlich normalerweise, daß diese Funktion spitze Ecken hat oder sogar Sprünge macht. (Also im anschaulichen Sinne nicht glatt ist.)
Um die Grenzwertbildung durchführen zu können, muß ich angeben können, wie nahe sich die zwei Orte, z.B. ) und und ) sind, genauer gesagt, ob sie sich durch Verkleinerung von sind, genauer gesagt, ob sie sich durch Verkleinerung von  "beliebig nahe" kommen können. Diese Frage wird u.a. von der topologischen Struktur der Raumzeit (oder des Raumes) beantwortet. (Fragen der Topologie ignoriere ich jetzt mal, da sich Physiker auf dieser Ebene sowieso nicht darum kümmern müssen.) Um dem Differenzenquotienten, dessen Grenzwert ich ausrechnen will, überhaupt einen Sinn geben zu können, brauche ich aber mindestens noch einen Vektorraum. Vektorräume (oder lineare Räume) sind die Objekte, deren Elemente ich addieren, voneinander abziehen, mit Zahlen multiplizieren oder durch Zahlen dividieren kann. Also genau das, was ich im Differenzenquotienten mache. Sie sind aber nicht allgemein genug, wenn man z.B. eine natürliche Einbeziehung des Äquivalenzprinzips in die Behandlung der Gravitation anstrebt. In diesem Fall ist die Raumzeit nicht mehr durch einen Vektorraum beschreibbar. Wir können also nicht so ohne weiteres die Differenzbildug zwischen dem Ort "beliebig nahe" kommen können. Diese Frage wird u.a. von der topologischen Struktur der Raumzeit (oder des Raumes) beantwortet. (Fragen der Topologie ignoriere ich jetzt mal, da sich Physiker auf dieser Ebene sowieso nicht darum kümmern müssen.) Um dem Differenzenquotienten, dessen Grenzwert ich ausrechnen will, überhaupt einen Sinn geben zu können, brauche ich aber mindestens noch einen Vektorraum. Vektorräume (oder lineare Räume) sind die Objekte, deren Elemente ich addieren, voneinander abziehen, mit Zahlen multiplizieren oder durch Zahlen dividieren kann. Also genau das, was ich im Differenzenquotienten mache. Sie sind aber nicht allgemein genug, wenn man z.B. eine natürliche Einbeziehung des Äquivalenzprinzips in die Behandlung der Gravitation anstrebt. In diesem Fall ist die Raumzeit nicht mehr durch einen Vektorraum beschreibbar. Wir können also nicht so ohne weiteres die Differenzbildug zwischen dem Ort  zur Zeit zur Zeit 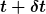 und dem Ort zur Zeit und dem Ort zur Zeit  in der Grundstruktur der Raumzeit zulassen. (D.h. wir könnten natürlich schon, aber dann müssen wir spätestens die ART aus unserer Betrachtung ausklammern.) in der Grundstruktur der Raumzeit zulassen. (D.h. wir könnten natürlich schon, aber dann müssen wir spätestens die ART aus unserer Betrachtung ausklammern.)
Die Idee bei der Einführung differenzierbarer Mannigfaltigkeiten ist nun, diese nützliche Vektorstruktur durch eine Art "lokale Linearisierung" der Raumzeit in diesem allgemeineren Zusammenhang wieder herzustellen. Das Resultat ist der Tangentialraum. Zur Veranschaulichung des Ergebnisses dieser Linearisierung kannst du dir immer eine glatte Fläche im Raum vorstellen (wie z.B. eine Kugeloberfläche), an die in einem Punkt eine Ebene tangential angelegt ist. Diese Ebene ist nichts anderes als eine normale euklidische Ebene, in der die bekannte euklidische, analytische Geometrie betrieben werden kann. Glatt, also ohne Kanten, muß sie deswegen sein, damit die Lage dieser Ebene eindeutig ist. Um den Zusammenhang nochmal klarzustellen: Linearisierung ist genau das, was ich brauche um zu addieren und zu subtrahieren, also Änderungen zu beschreiben, und es ist genau das, was ich erhalte, wenn ich sinnvoll über Grenzwerte von Ortsänderungen sprechen kann. Und um sinnvoll über Ortsänderungen (als Grenzwert) reden zu können, benötige ich irgendeine Form von "Glattheit". Beide Begriffe (Linearität und Glattheit) werden also in diesem Zusammenhang aufeinander zurückgeführt.
Soweit zur Veranschaulichung. Die Schwierigkeit besteht nun eigentlich hauptsächlich darin, diese "Glattheit" durch Begriffe einzufangen, die sich ausschließlich auf das "Innere" der Raumzeit beziehen und keinen Bezug zu umgebenden Vektorräumen haben, wie dem dreidimensionalen Raum im Fall der Kugelfläche. Wenn wir um den Ort  Koordianten Koordianten ) (Lies: "i-te Koordinate vom Ort (Lies: "i-te Koordinate vom Ort  ") errichten können, sind wir zumindest in der Lage, die Änderung dieser Koordinaten ") errichten können, sind wir zumindest in der Lage, die Änderung dieser Koordinaten  = \kappa^i(\mathbf{r}(t))) zu untersuchen zu untersuchen
 - x^i(t),)
denn das sind ja normale Zahlen, deren Differenz ich bilden kann.
Die Glattheit dieser Funktionen ) bedeutet nun genau, daß ich die Änderung ihres Funktionswertes infolge einer Änderung von bedeutet nun genau, daß ich die Änderung ihres Funktionswertes infolge einer Änderung von  nach nach 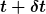 durch Polynome durch Polynome
 = a_0(t) + a^i_1(t)\delta t + a^i_2(t)\delta t^2 + \ldots + a^i_n(t)\delta t^n)
beliebig hoher Ordnung n, zu jedem beliebigen Zeitpunkt, beliebig genau approximieren kann, d.h. der Approximationsfehler
 - p^i_n(\delta t) = R^i_n(t, \delta t))
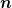 -ter Ordnung geht schneller gegen null als -ter Ordnung geht schneller gegen null als  . Aus dieser Approximationseigenschaft . Aus dieser Approximationseigenschaft
 = a^i_0(t) + a^i_1(t)\delta t + a^i_2(t)\delta t^2 + ... + R^i_n(t, \delta t))
folgen eine Reihe angenehmer Eigenschaften von 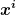 , nämlich u.a. , nämlich u.a.
 = \lim_{\delta t\to 0} x^i(t+\delta t) = x^i(t)) (Stetigeit) (Stetigeit)
 = \lim_{\delta t\to 0} \frac{x^i(t+\delta t) - a^i_0(t)}{\delta t} = \dot x^i(t)) (Differenzierbarkeit) (Differenzierbarkeit)
 = \lim_{\delta t\to 0} \frac{x^i(t+\delta t) - a^i_0(t)-a^i_1(t)\delta t}{\delta t^2} = \lim_{\delta t\to 0}\frac{\dot x^i(t+\delta t)-a^i_1(t)}{2\delta t} = \frac{1}{2}\ddot x^i(t)) (nochmalige Differenzierbarkeit) (nochmalige Differenzierbarkeit)
etc. Als glatte Funktion besitzt 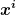 also Ableitungen beliebig hoher Ordnung. (Ursprünglich habe ich die Funktion ja glatt genannt, wenn ihre erste Ableitung existiert. Man sagt auch, die Funktion sei "hinreichend glatt" um auszudrücken, daß sie diese Approximationseigenschaft zumindest bis zu der Ordnung besitzt, die man gerade unbedingt braucht. Also je nach Zusammenhang bis zur ersten, zweiten, 100sten oder beliebiger Ordnung.) also Ableitungen beliebig hoher Ordnung. (Ursprünglich habe ich die Funktion ja glatt genannt, wenn ihre erste Ableitung existiert. Man sagt auch, die Funktion sei "hinreichend glatt" um auszudrücken, daß sie diese Approximationseigenschaft zumindest bis zu der Ordnung besitzt, die man gerade unbedingt braucht. Also je nach Zusammenhang bis zur ersten, zweiten, 100sten oder beliebiger Ordnung.)
Was habe ich nun davon? Ich möchte eine Kurve ) durch die Raumzeit als "glatt" bezeichnen können um ihren Geschwindigkeitsvektor angeben zu können. Was ich bis jetzt tun kann, ist, zu untersuchen, ob die Koordinaten durch die Raumzeit als "glatt" bezeichnen können um ihren Geschwindigkeitsvektor angeben zu können. Was ich bis jetzt tun kann, ist, zu untersuchen, ob die Koordinaten ) glatte Kurven in glatte Kurven in  bilden und in diesem Fall den "Koordinatenvektor" bilden und in diesem Fall den "Koordinatenvektor" ) zu jedem Zeitpunkt ausrechnen. Ideal wäre es natürlich nun, wenn ich die Kurve selbst als "glatt" bezeichnen könnte, sofern ihre zugehörigen Koordinatenfunktionen glatt sind, und wenn ich die "Koordinatenvektoren" zu jedem Zeitpunkt ausrechnen. Ideal wäre es natürlich nun, wenn ich die Kurve selbst als "glatt" bezeichnen könnte, sofern ihre zugehörigen Koordinatenfunktionen glatt sind, und wenn ich die "Koordinatenvektoren" ) irgendwie sinnvoll mit dem zu definierenden Geschwindigkeitsvektor in Beziehung setzen könnte. Das einzige Problem, das dieser Absicht im Wege stehen könnte, ist, daß ich um jeden Punkt eine weiteres Kooridnatensystem irgendwie sinnvoll mit dem zu definierenden Geschwindigkeitsvektor in Beziehung setzen könnte. Das einzige Problem, das dieser Absicht im Wege stehen könnte, ist, daß ich um jeden Punkt eine weiteres Kooridnatensystem =\bar\kappa^i(\mathbf{r}(t))) errichten könnte und niemand garantiert, daß die Funktionen errichten könnte und niemand garantiert, daß die Funktionen ) ebenfalls glatt sind. Was tut man also? Nichts weiter als zu fordern, daß zwischen allen zulässigen Koordinatensystemen die Übergänge ebenfalls glatt sein müssen. (Die Übergänge zwischen zwei Koordinatensystemen bilden eine Menge von Zahlen auf eine andere Menge von Zahlen ab. Es gibt also kein Problem mit der Definition von Glattheit.) Das bedeutet folgendes: ich kann ja dieselbe Kurve ebenfalls glatt sind. Was tut man also? Nichts weiter als zu fordern, daß zwischen allen zulässigen Koordinatensystemen die Übergänge ebenfalls glatt sein müssen. (Die Übergänge zwischen zwei Koordinatensystemen bilden eine Menge von Zahlen auf eine andere Menge von Zahlen ab. Es gibt also kein Problem mit der Definition von Glattheit.) Das bedeutet folgendes: ich kann ja dieselbe Kurve ) sowohl durch das eine Koordinatensystem sowohl durch das eine Koordinatensystem  = \kappa^i(\mathbf{r}(t))) als auch durch das andere Koordinatensystem als auch durch das andere Koordinatensystem =\bar\kappa^i(\mathbf{r}(t))) ausdrücken. Jedes dieser beiden Koordinatentupel, z.B. ausdrücken. Jedes dieser beiden Koordinatentupel, z.B. ) , legt eindeutig fest auf welchen Punkt , legt eindeutig fest auf welchen Punkt ) es sich bezieht, und zu diesem Punkt gehört ebenso das andere Koordinatentupel es sich bezieht, und zu diesem Punkt gehört ebenso das andere Koordinatentupel ) . Die Koordinaten lassen sich also eindeutig ineinander umrechnen . Die Koordinaten lassen sich also eindeutig ineinander umrechnen
 \mapsto \mathbf{r}(t)\mapsto y^i(t).)
Diese Umrechnung bezeichne ich mit =y^i(x^1(t), \ldots, x^n(t))=y^i(x^k(t))) . (Das ist mehrdeutige Physikerschreibweise, führt aber zu leicht zu merkenden Formeln.) Wenn nun, wie gesagt, diese Umrechnung glatt ist, muß die Koordinatenkurve . (Das ist mehrdeutige Physikerschreibweise, führt aber zu leicht zu merkenden Formeln.) Wenn nun, wie gesagt, diese Umrechnung glatt ist, muß die Koordinatenkurve ) glatt sein, sofern die ursprüngliche Koordinatenkurve glatt sein, sofern die ursprüngliche Koordinatenkurve ) glatt war. Wenn ich ausschließlich glatte Koordinatenwechsel zulasse, spielt es für die Glattheit also überhaupt keine Rolle welches Koordinatensystem ich verwende und ich kann einfach behaupten, daß die Kurve glatt war. Wenn ich ausschließlich glatte Koordinatenwechsel zulasse, spielt es für die Glattheit also überhaupt keine Rolle welches Koordinatensystem ich verwende und ich kann einfach behaupten, daß die Kurve ) selbst glatt ist, sofern sie bzgl. irgendeines Koordinatensystems glatt ist. In diesem Fall existieren auch immer alle Koordinatenableitungen nach selbst glatt ist, sofern sie bzgl. irgendeines Koordinatensystems glatt ist. In diesem Fall existieren auch immer alle Koordinatenableitungen nach  und ich kann mit der Kettenregel argumentieren, daß und ich kann mit der Kettenregel argumentieren, daß
 = \frac{\partial y^i}{\partial x^1}\dot x^1(t) + \cdots + \frac{\partial y^i}{\partial x^n}\dot x^n(t).\qquad (*))
Die Koordinatenableitungen bilden sich also unter allen zulässigen Koordinatentransformationen linear und eindeutig aufeinander ab. Insbesondere ist also die transformierte Summe von zwei Koordintenableitungen (zweier verschiedener Kurven) gleich der Summe der transformierten Koordinatenableitungen. Das ist genau das, was man von Vektoren erwarten würde. Hier steckt also eine lineare Struktur verborgen. Wir können also beliebige Zahlentupel  als Vektoren bezeichnen, wenn wir 1) sagen auf welches Koordinatensystem sie sich beziehen und 2) fordern, daß ihnen bzgl. jedes anderen Koordinatensystems dasjenige Tupel entspricht, welches aus dem ersten durch die lineare Transformation als Vektoren bezeichnen, wenn wir 1) sagen auf welches Koordinatensystem sie sich beziehen und 2) fordern, daß ihnen bzgl. jedes anderen Koordinatensystems dasjenige Tupel entspricht, welches aus dem ersten durch die lineare Transformation ) hervorgeht. hervorgeht.
Wir erhalten also für jede Kurve zum Zeitpunkt  eine ganze Familie äquivalenter Tupel zusammen mit den sie definierenden Koordinatensystemen eine ganze Familie äquivalenter Tupel zusammen mit den sie definierenden Koordinatensystemen
, \kappa^i)\simeq (\dot y^i(t), \bar \kappa^i).)
Und diese Familie von Tupeln zusammen mit ihren jeweiligen Koordinatensystemen nennt man den Tangentialvektor an die Kurve im Punkt ) . Zwei solcher Tangentialvektoren kann ich addieren und wegen dem Transformationsgesetz . Zwei solcher Tangentialvektoren kann ich addieren und wegen dem Transformationsgesetz ) ist das Ergebnis eine Familie von Tupeln, deren Mitglieder jeweils die Summen der entsprechenden Mitglieder der einzelnen Summanden sind. Die Tupel ist das Ergebnis eine Familie von Tupeln, deren Mitglieder jeweils die Summen der entsprechenden Mitglieder der einzelnen Summanden sind. Die Tupel  selbst, bezeichnet man als Komponenten dieses Vektors bzgl. der Koordinaten selbst, bezeichnet man als Komponenten dieses Vektors bzgl. der Koordinaten  . .
Den Vektorraum aus allen Tangentialvektoren an einem festen Punkt bezeichnet man als Tangentialraum in diesem Punkt. Er ist eine etwas abstrakte (aber intrinsische, also ohne externen Bezug konstruierte) Verallgemeinerung der Tangentialebene an eine Kugeloberfläche.
Eine Menge von zulässigen Koordiatensystemen in einem Punkt ermöglicht also die lokale Linearisierung der Raumzeit in diesem Punkt. Eine maximale Menge von zulässigen Koordinatensystemen, aus der mindestens eines um jeden Punkt errichtet werden kann, heißt "differenzierbare Struktur" der Raumzeit. Diese ist also dir Grundlage für die lokale Linearisierung der gesamten Raumzeit.
Zusammenfassung: erste Mindestanforderung an die Raumzeitgeometrie ist die Möglichkeit glatte Koordinatensysteme einzuführen. Diese Koordinatensysteme müssen eine differenzierbare Struktur auf der Raumzeit bilden. Dann kann ich glatte Kurven und deren Tangentialvektoren (also momentane Geschwindigkeitsvektoren) definieren.
So, das war jetzt schon mal ein ganzes Stück Arbeit. Der affine Zusammenhang erfordert mindestens nochmal ebenso viel. Das schaffe ich heute aber nicht mehr.
Fortsetzung folgt, wenn du noch Lust hast...
|
|
 |
G4mm4G0bl1n
Anmeldungsdatum: 10.05.2017
Beiträge: 93
Wohnort: Darmstadt
|
 G4mm4G0bl1n Verfasst am: 11. Mai 2017 13:02 Titel: G4mm4G0bl1n Verfasst am: 11. Mai 2017 13:02 Titel: |
 |
|
Statt das hier immer nur Formeln gepostet werden. Wieso übersetzt es denn keiner in die klassische Mathematik und visualisiert es dann mit einem Computer? Ich kann vorher niemandem abkaufen, dass er es wirklich verstanden hat.
Stellt eure Funktionen doch mal durch eine Trigonometrische Reihe da. Riemann bewies bereits, dass dies ohne Einschränkung möglich ist und es geht auch bei der Herleitung der Raumzeit.
https://www.emis.de/classics/Riemann/Trig.pdf
Aussehen tut das ganze dann wie in geposteten Bildern. (Der Tangentialvektor bezieht sich übrigens nur auf die Achsen X & Y , aber das sollte ja aus vorangegangenen Formeln ersichtlich sein)
Die Bilder wurden übrigens durch fxcalc visualisiert.
| Beschreibung: |
|

Download |
| Dateiname: |
spacetime1.png |
| Dateigröße: |
132.46 KB |
| Heruntergeladen: |
219 mal |
| Beschreibung: |
|

Download |
| Dateiname: |
spacetime0.png |
| Dateigröße: |
18.72 KB |
| Heruntergeladen: |
173 mal |
|
|
 |
|
|















