| Autor |
Nachricht |
Neuling_2015
Gast
|
 Neuling_2015 Verfasst am: 01. Jan 2016 18:19 Titel: Kreuzprodukt Nabla und ebene Welle Neuling_2015 Verfasst am: 01. Jan 2016 18:19 Titel: Kreuzprodukt Nabla und ebene Welle |
 |
|
Hallo, ich habe eine Frage mathematischer Natur, welche mir nicht ganz klar erscheint.
Wir nehmen an, wir haben die Gleichung für das B-Feld:
 e^{i\left(\vec k \vec r - \omega t\right)})
Um das E-Feld daraus zu bestimmen, muss ich die Rotation dieses Feldes bilden. Das kann man jetzt komponentenweise machen und kommt dann auf etwas, was folgende Gleichung bestätigt:

Die Frage ist jetzt: Warum ist das so?
Das es stimmt kann man leicht durch einsetzen der Gleichung für das B-Feld überprüfen. Aber es ist ja nicht zufällig so, sondern es muss ja eine mathematische Begründung dahinter stehen.
Man sieht leicht, das gilt:

Aber wieso kann ich diesen Term dann einfach mit dem Nabla ersetzen und das Kreuzprodukt stehen lassen? Wäre klasse, wenn mir das jemand erklären könnte. Ist ja nützlich wenn man weiß was dahinter steckt und man nicht komponentenweise Ergebnisse berechnen muss.
Frohes Neues Jahr an Alle.  |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Jan 2016 00:04 Titel: index_razor Verfasst am: 02. Jan 2016 00:04 Titel: |
 |
|
Die Antwort hängt sehr stark von deinem Vorwissen ab. Letztendlich ist das Resultat die Folge einer Produktregel, die in der klassischen Vektoranalysis die Form
 = \phi \nabla\times\vec{A} - \vec{A}\times\nabla\phi)
annimmt, wenn man diese auf den Spezialfall anwendet, daß i) 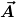 konstant ist und man ii) für den Gradienten von konstant ist und man ii) für den Gradienten von ) die Formel verwendet, die du selbst benutzt hast. Das führt allerdings nur zur Frage, warum diese Produktregel gilt. Auch diese kann mit elementaren Mitteln kaum anders bewiesen werden, als durch komponentenweises ausrechnen in kartesischen Koordinaten. die Formel verwendet, die du selbst benutzt hast. Das führt allerdings nur zur Frage, warum diese Produktregel gilt. Auch diese kann mit elementaren Mitteln kaum anders bewiesen werden, als durch komponentenweises ausrechnen in kartesischen Koordinaten.
Verständlicher werden diese und andere Formeln m.E. wenn man sie als Ausprägung von Eigenschaften der äußeren Ableitung auf geeigneten äußeren Algebren versteht. Diese Algebren erlauben die Multiplikation von Vektoren (Vektorfeldern oder Differentialformen) zu Objekten "höheren Grades" mittels einer Verallgemeinerung des Kreuzprodukts -- des sogenannten äußeren Produkts  . Die "Kommutativität" des Produkts ist dabei abhängig vom Grad der beiden Faktoren. So vertauscht es z.B. wenn einer der Faktoren eine Funktion (Grad null) ist, aber es ist antisymmetrisch, wie das Kreuzprodukt, wenn beide Faktoren Vektoren (Grad 1) sind. . Die "Kommutativität" des Produkts ist dabei abhängig vom Grad der beiden Faktoren. So vertauscht es z.B. wenn einer der Faktoren eine Funktion (Grad null) ist, aber es ist antisymmetrisch, wie das Kreuzprodukt, wenn beide Faktoren Vektoren (Grad 1) sind.
Die äußere Ableitung 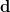 läßt sich für Objekte beliebigen Grades auf der Algebra definieren und beinhaltet alle "Nabla-Operatoren" der klassischen Vektoranalysis, wie Gradient, Divergenz und Rotation, je nachdem auf Objekte welchen Grades man sie anwendet: Sie ergibt den Gradienten für Objekte vom Grad 0 (Funktionen), die Rotation für Objekte vom Grad 1 (Vektoren) und die Divergenz für Objekte vom Grad 2 ("2-Formen") und sie ergibt immer null für Objekte vom Grad 3 (wenn der Vektorraum 3-dimensional ist). Sie erfüllt außerdem die Produktregel läßt sich für Objekte beliebigen Grades auf der Algebra definieren und beinhaltet alle "Nabla-Operatoren" der klassischen Vektoranalysis, wie Gradient, Divergenz und Rotation, je nachdem auf Objekte welchen Grades man sie anwendet: Sie ergibt den Gradienten für Objekte vom Grad 0 (Funktionen), die Rotation für Objekte vom Grad 1 (Vektoren) und die Divergenz für Objekte vom Grad 2 ("2-Formen") und sie ergibt immer null für Objekte vom Grad 3 (wenn der Vektorraum 3-dimensional ist). Sie erfüllt außerdem die Produktregel
 = \dd a\wedge b +(-)^n a\wedge \dd b,)
wobei 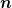 der Grad von der Grad von  ist. Wenn du alle diese Aussagen zusammenzählst, kannst du mit Hilfe dieser verallgemeinerten Produktregel auf der äußeren Algebra die obige Produktregel der klassischen Vektoranalysis schon fast beweisen oder zumindest plausibel machen. ist. Wenn du alle diese Aussagen zusammenzählst, kannst du mit Hilfe dieser verallgemeinerten Produktregel auf der äußeren Algebra die obige Produktregel der klassischen Vektoranalysis schon fast beweisen oder zumindest plausibel machen.
Bei entsprechender Neigung empfehle ich dir, dich eingehender mit dem Differentialformenkalkül zu beschäftigen. Dort sind die Zusammenhänge der verschiedenen Identitäten der Vektoranalysis auf eine einheitliche Grundlage gestellt. |
|
 |
Neuling_2015
Gast
|
 Neuling_2015 Verfasst am: 02. Jan 2016 14:42 Titel: Neuling_2015 Verfasst am: 02. Jan 2016 14:42 Titel: |
 |
|
Vielen Dank erstmal für die ausführliche Erklärung. Das klingt erstmal sehr interessant und auch das Differentialformenkalkül werde ich mir mal anschauen. Ich denke die Grundidee zu durchschauen muss mich aber damit etwas mehr befassen, da das ganze durch das äußere Produkt eine ganze Stufe abstrakter wird wie ich finde.
Das heißt also, diese Produktregel kann ich immer verwenden in derartigen Fällen (also vorallem bei B-Feld aus E-feld berechnen oder andersrum ähneln sich die Strukturen ja)?
Dann noch eine Frage zur direkten Anwendung:
Wenn ich entsprechend einsetze erhalte ich ja sowas:
 = \vec \nabla \times B_0\left( \vec e_x - i \vec e_y \right)e^{i\vec k \vec r} = \phi\vec\nabla \times \vec A - \vec A \times \vec\nabla\phi)
e^{i\vec k \vec r} = - B_0\left( \vec e_x - i \vec e_y \right) \times\vec\nabla e^{i\vec k \vec r} = - B_0\left( \vec e_x - i \vec e_y \right) \times i\vec ke^{i\vec k \vec r}= i\vec ke^{i\vec k \vec r}\times B_0\left( \vec e_x - i \vec e_y \right))
Wieso kann ich jetzt das Skalar (die e-Funktion) auf die andere Seite durchtauschen?
Danke dir 
PS: Wenn du so fit bist, was diese mathematischen Sachen angeht, könntest du mir vielleicht auch bei dem anderen Thread von gestern helfen!?  |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Jan 2016 17:30 Titel: index_razor Verfasst am: 02. Jan 2016 17:30 Titel: |
 |
|
| Neuling_2015 hat Folgendes geschrieben: |
Das heißt also, diese Produktregel kann ich immer verwenden in derartigen Fällen
|
Die Produktregel für die äußere Ableitung ist universell. Die spezielle Form für ) gilt eben nur für das Produkt aus Vektor (eigentlich in diesem Fall "Pseudovektor" oder 2-Form) und Funktion, dessen Rotation du berechnen willst. gilt eben nur für das Produkt aus Vektor (eigentlich in diesem Fall "Pseudovektor" oder 2-Form) und Funktion, dessen Rotation du berechnen willst.
| Zitat: |
(also vorallem bei B-Feld aus E-feld berechnen oder andersrum ähneln sich die Strukturen ja)?
|
Ich bin mir nicht sicher, ob ich verstehe was du meinst. Aber sagen wir mal, daß die Maxwellgleichungen ohne weiteres mit Hilfe der äußeren Ableitung formuliert werden können. Also in diesem Sinne eignet sich der Kalkül wunderbar zur "Berechnung von E-Feld und B-Feld". Wenn du noch ein paar Anhaltspunkte willst, wie das genau funktioniert, kann ich gern noch mehr dazu schreiben.
| Zitat: |
Dann noch eine Frage zur direkten Anwendung:
Wenn ich entsprechend einsetze erhalte ich ja sowas:
 = \vec \nabla \times B_0\left( \vec e_x - i \vec e_y \right)e^{i\vec k \vec r} = \phi\vec\nabla \times \vec A - \vec A \times \vec\nabla\phi)
e^{i\vec k \vec r} = - B_0\left( \vec e_x - i \vec e_y \right) \times\vec\nabla e^{i\vec k \vec r} = - B_0\left( \vec e_x - i \vec e_y \right) \times i\vec ke^{i\vec k \vec r}= i\vec ke^{i\vec k \vec r}\times B_0\left( \vec e_x - i \vec e_y \right))
Wieso kann ich jetzt das Skalar (die e-Funktion) auf die andere Seite durchtauschen?
|
Das Kreuzprodukt ist bilinear:
i)  = (\phi\vec{a})\times\vec{b} = \vec{a}\times(\phi\vec{b}),)
ii) \times\vec{c} = \vec{a}\times\vec{c} + \vec{b}\times\vec{c}) |
|
 |
|
|


















