| Autor |
Nachricht |
Mr Maths
Anmeldungsdatum: 15.05.2011
Beiträge: 110
|
 Mr Maths Verfasst am: 19. Okt 2015 20:28 Titel: Taylorentwicklung für Grenzbetrachtung? |
 |
|
Hallo,
ich habe hier folgende Gleichung =\frac{b}{a}*(1-e^{-at}))
Ich verstehe nicht, was für t->0 und t->\infty eine Taylorentwicklung hier bringen soll, denn ich kann auch mit Limes das machen. Was ist der Unterschied.
Z.B. Taylorentwicklung mit t->0 ergibt folgendes:  = \frac{b}{a}*(1-(1-at)) = \frac{b}{a}*at = bt)
Folgendes verstehe ich unter Taylorentwicklung:
Gegeben sei eine Funktion f und diese kann man dann dann als Addition mehrer Terme darstellen und so angenähert werden, also eine sog. "Taylor-Reihe".
Könnt ihr mir da weiterhelfen bitte?
Gruß
Mr-Maths |
|
 |
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3405
|
| ML Verfasst am: 19. Okt 2015 21:59 Titel: Re: Taylorentwicklung für Grenzbetrachtung? |
|
|
Hallo,
| Mr Maths hat Folgendes geschrieben: |
ich habe hier folgende Gleichung =\frac{b}{a}\cdot (1-e^{-at}))
Ich verstehe nicht, was für t->0 und t->\infty eine Taylorentwicklung hier bringen soll,
|
Sie soll Dir die Berechnung des Grenzwertes erleichtern. Nehmen wir das Beispiel t-->0. Die Taylorreihe der e-Funktion lautet bei einer Entwicklung um den Entwicklungspunkt 0:
Wir brechen die Taylorreihe nach dem linearen Glied ab. Dadurch machst Du natürlich grundsätzlich einen Fehler. Der Clou ist aber, dass dieser Fehler für t-->0 (den Entwicklungspunkt!) immer kleiner wird und schließlich nach dem Grenzübergang verschwindet.
Praktisch gesehen kannst Du also den Term 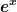 in der Umgebung von Null durch 1+x ersetzen. Dadurch ergibt sich bei der Grenzwertbetrachtung:
 = \lim\limits_{t\to 0} \frac{b}{a}\cdot \left(1-(1-at) \right) = \lim\limits_{t\to 0} \frac{b}{a}\cdot at = \lim\limits_{t\to 0} b\cdot t = 0)
Das Ergebnis "Null" war vorher auch klar. Du weißt aber nun zusätzlich, wie schnell die Funktion gegen null konvergiert.
Im Falle von ) hast Du über den Taylorreihenansatz eine Alternative zur Regel von de l'Hospital zur Verfügung.
Viele Grüße
Michael |
|
|
Mr Maths
Anmeldungsdatum: 15.05.2011
Beiträge: 110
|
| Mr Maths Verfasst am: 19. Okt 2015 23:00 Titel: |
|
|
Hmm okay danke, aber folgendes verstehe ich noch nicht:
1. Was meint man mit dem "Entwicklungspunkt 0"? Kann man den grafisch sehen irgendwo?
2. Wie weiß man, nach welchem Glied ich abbrechen muss? Eigentlich je mehr Glieder ich habe desto genauer ist die Funktion an die originiale angepasst, bei unendlich Gliedern ist diese 100% identisch. |
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3405
|
| ML Verfasst am: 19. Okt 2015 23:55 Titel: |
|
|
Hallo,
| Mr Maths hat Folgendes geschrieben: | Hmm okay danke, aber folgendes verstehe ich noch nicht:
1. Was meint man mit dem "Entwicklungspunkt 0"? Kann man den grafisch sehen irgendwo?
|
Du kannst ihn selbst bei der Reihenentwicklung festlegen. Wenn Du eine Funktion f(x) in eine Reihe entwickeln willst, fängst Du mit irgendeinem Funktionswert als allererster Näherung an und sagst: f(x) = f(x_0) + Korrekturterm, also f(x) ist näherungsweise gleich dem Wert am Entwicklungspunkt x_0 plus irgendeinem Korrekturterm. Anschließend ergänzt Du immer mehr Terme der Taylorreihe mit dem Ziel, den Korrekturterm kleiner machen zu können.
siehe: https://de.wikipedia.org/wiki/Taylorreihe#Definition
Im Beispiel mit der e-Funktion, die wir um 0 entwickeln, sagen wir also:
exp(x) = exp(0) + Korrekturterme.
Der Summand 1 in der Reihenentwicklung ist das exp(0).
| Zitat: |
2. Wie weiß man, nach welchem Glied ich abbrechen muss? Eigentlich je mehr Glieder ich habe desto genauer ist die Funktion an die originiale angepasst, bei unendlich Gliedern ist diese 100% identisch. |
Global betrachtet musst Du alle Terme nehmen, wenn Du exakt bleiben willst; und dann ist je nach Fragestellung immer noch entscheidend, ob die Reihe gleichmäßig konvergiert oder nur punktweise.
https://de.wikipedia.org/wiki/Gleichm%C3%A4%C3%9Fige_Konvergenz
Lokal betrachtet (d. h. in einer unendlich kleinen Umgebung um Deinen gewünschten x-Wert) kannst Du differenzierbare Funktionen aber grundsätzlich durch eine lineare Funktion (ihre Tangente) approximieren. Das haben wir im obigen Beispiel mit der E-Funktion genau so gemacht, indem wir e^x in der Nähe von Null durch 1+x ersetzt haben.
Viele Grüße
Michael |
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 20. Okt 2015 14:08 Titel: |
|
|
| Mr Maths hat Folgendes geschrieben: |
2. Wie weiß man, nach welchem Glied ich abbrechen muss? Eigentlich je mehr Glieder ich habe desto genauer ist die Funktion an die originiale angepasst, bei unendlich Gliedern ist diese 100% identisch. |
Nein, das ist nicht garantiert. Funktionen mit dieser Eigenschaft heißen "analytisch". Es gibt aber Funktionen, die zwar unendlich oft differenzierbar sind, deren Taylor-Approximation in bestimmten Punkten aber auch für beliebig hohe Ordnungen immer gleich schlecht bleibt und sich nie der Funktion annähert. Ein Beispiel ist
 = \left\{ \begin{matrix} e^{-1/x}, & \text{für}\ x>0, \\ 0 &, \text{für}\ x \leq 0\end{matrix}\right.
<br />
)
Alle Ableitungen an der Stelle x=0 sind null, also ist auch die Taylorreihe identisch null, sie stimmt also in keiner Umgebung um null mit der Funktion überein.
Ein anderes pathologisches Beispiel ist
 = \frac{1}{1+x^2}
<br />
)
Diese Funktion ist überall auf R definiert und beliebig oft differenzierbar, ihre Taylorreihe im Punkt x=0 hört aber bei |x|=1 auf zu konvergieren.
Der Zusammenhang zwischen Differenzierbarkeit und Analytizität wird erst im Komplexen (Funktionentheorie) zufriedenstellend geklärt. Dort sind beide Begriffe überraschenderweise synonym. Die Exponentialfunktion ist übrigens analytisch (und wird oft sogar einfach durch ihre Taylorreihe definiert). Da funktioniert also alles wunderbar.
Wann man die Taylorapproximation abbrechen kann, ist wohl allgemein nicht so leicht zu beantworten. Der Satz von Taylor garantiert nur, daß nach dem n-ten Glied der Fehler nicht stärker wächst als ) . Das gilt aber auch für die beiden Funktionen oben, über die Qualität der Approximation ist damit also noch nicht viel ausgesagt. Es hängt alles vom Verhalten der Ableitungen in der Umgebung des Entwicklungspunktes ab. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
