| Autor |
Nachricht |
Kir
Gast
|
 Kir Verfasst am: 16. Jul 2015 22:55 Titel: Hat die Standardabweichung einen Fehler? Kir Verfasst am: 16. Jul 2015 22:55 Titel: Hat die Standardabweichung einen Fehler? |
 |
|
Meine Frage:
Servus,
aktuell beschäftigt mich eine kleine Frage, die ich bis jetzt leider auch noch nicht so gefunden habe. (Sorry, falls sie doch schonmal irgendwo war. Habe zwar viele ähnliche Fragen gefunden, aber nicht genau die.)
Sagen wir mal, ich habe eine Messreihe  und und 
Nun möchte ich dafür einen Fehler abschätzen. Das wäre ja in dem Fall über die Stanartabweichung machbar. Nun ist die Stanartabweichung aber abhängig vom Durchschnitt 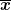 und von und von  . Beide Größen haben aber nun auch einen Fehler. . Beide Größen haben aber nun auch einen Fehler.
Was ich mich nun Frage: Macht es eigentlich Sinn, wenn ich den Fehler der Größen wieder durch die Stanartabweichung ziehe?
Meine Ideen:
Ich hätte jetzt gesagt:
^{2}}{n - 1}}\\
<br />
\Delta \sigma &= \left| \frac{d\sigma}{d\overline{x}} \right| \Delta \overline{x} + \sum_{i = 1}^{n} \left| \frac{d\sigma}{d\overline{x}} \right| \Delta x_{i}
<br />
)
Und als Gesamtfehler
^{2} + \sqrt{\sigma^{2} + (\Delta \sigma)^{2}}})
Aber macht das jetzt eigentlich als Messfehler Sinn? Oder mittelt sich das alles irgendwo raus? Weil irgendwie scheint das für mich wie "Fehler vom Fehler". Aber auf der anderen Seite würde ich auch sagen, dass die Stanartabweichung fehlerbehaftet ist. Oder doch nicht? |
|
 |
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
 Ich Verfasst am: 17. Jul 2015 09:35 Titel: Ich Verfasst am: 17. Jul 2015 09:35 Titel: |
 |
|
Google doch mal:
standardabweichung fehlerbehafteter größen |
|
 |
Kir
Gast
|
 Kir Verfasst am: 17. Jul 2015 19:01 Titel: Kir Verfasst am: 17. Jul 2015 19:01 Titel: |
 |
|
Das habe ich bereits gemacht, konnte aber nichts für meine genaue Frage finden. Dass man normalerweiße einfach den Mittelwertfehler und die Stanartabweichung quadratisch addiert, ist mir bekannt.
Was mich einfach wundert ist, dass niemand Standardabweichung selbst als fehlerbehaftet ansieht. Obwohl die Standardabweichung selbst eine Funktion vom Mittelwert und der Messwerte ist. Ich frage mich halt einfach, ob der Fehler in der Regel einfach ignoriert wird, oder ob es dafür tatsächlich einen Grund gibt, dass der nicht mit rein kommt. |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 17. Jul 2015 19:33 Titel: as_string Verfasst am: 17. Jul 2015 19:33 Titel: |
 |
|
Ich würde es eher umgekehrt sehen:
Wenn Du eine Messung hast und für die durch die Fehlerfortpflanzung einen Messfehler auf Grundlage der Fehler für die Eingangswerte berechnet hast. Andererseits aber die Messung tausende Male durchführst und den Fehler dieser Messreihe ausrechnen kannst rein aus der Statistik von den tausend identisch durchgeführten Einzelmessungen. Dann ist der Fehler für die Einzelmessung natürlich schon größer als für die ganze Reihe. Wenn Du aber aus der Reihe dann den Fehler einer Einzelmessung zurück rechnest und mit dem Fehler vergleichst, den Du aus der Fortpflanzung hast, dann sollten die (im Idealfall...) etwa übereinstimmen.
Wenn Du eine Messung so wie so sehr häufig ausführen kannst, brauchst Du eigentlich die Fehlerfortpflanzung für diese Werte nicht weiter beachten. Der Wert, den Du aus der Statistik bekommst, sollte i. A. richtiger sein.
Anders ist es, wenn Du einen Messwert aus unterschiedlichen Einzelmessungen bestimmen willst. Z. B. kann ein Smartphone seine Position aufgrund verschiedener Informationen bestimmen: Einmal die der Mobilfunk-Sendemast-Position und der jeweiligen Signalstärke (durch Triangulierung), dann durch die Empfangsstärke verschiedener WLAN-Netzwerke in der Nähe und dann natürlich durch GPS. Diese drei Methoden sind sehr unterschiedlich in ihrer Genauigkeit und sogar sehr unterschiedlich je nach Ort und Zeit an dem man die Position messen will (wenn nur ein WLAN in der Nähe ist und das eher schwach aber eine große Dichte an Mobilfunk-Empfangsmasten, z. B.).
Da gewichtet man sinniger Weise die drei Messwerte entsprechend ihrer Genauigkeit und zwar so, dass die Standardabweichung möglichst gering wird, indem man in die Mittelwertberechnung die jeweiligen Fehler der Einzelmessungen berücksichtigt. Da es unterschiedliche Messwerte mit unterschiedlichen Fehlern sind, würde es falsch sein, einfach die obige Formel zu verwenden. Außerdem sind es hier ja auch nur 3 Werte, so dass die Statistik zu gering ist, überhaupt eine sinnvolle Aussage über Standardabweichung o. Ä. zu treffen...
Gruß
Marco |
|
 |
Kir
Gast
|
 Kir Verfasst am: 18. Jul 2015 21:23 Titel: Kir Verfasst am: 18. Jul 2015 21:23 Titel: |
 |
|
|
Ahh, ok. Ich glaube mir ist das klar geworden. Danke sehr. |
|
 |
FehlerGast
Gast
|
 FehlerGast Verfasst am: 16. Feb 2016 14:11 Titel: FehlerGast Verfasst am: 16. Feb 2016 14:11 Titel: |
 |
|
Hallo,
ich wärme das Thema nochmal auf:
Grundsätzlich kann ich die Argumentation nachvollziehen und würde es für identische Einzelmessungen bzw. eine pure Wiederholung von identischen Experimenten genauso sehen wie as_string.
Wie aber sieht es mit der statistischen Auswertung von Größen aus, für die ich eine Verteilung habe. Nehmen wir an, ich schaue mir unter dem Mikroskop eine Menge von Partikeln an, deren Größe ich nun ausmesse. Angenommen ich habe alle Partikel in einem Verfahren hergestellt und möchte nun ihre Größenverteilung wissen. Dann kann ich zum Beispiel den Durchmesser von 100 dieser Partikel messen, einen Mittelwert und eine Standardabweichung für diese Messung angeben. Diese definiert mir meine Partikelverteilung. Ist darin jetzt schon der Messfehler enthalten oder nicht?
Angenommen meine Verteilung ist sehr eng und das Ergebnis meiner Messung lautet (10 +/- 1) µm und mein/e Auflösung/Maßstab erlaubt mir aber nur auf 1 µm genau zu messen, muss ich dann den Fehler noch hinzu rechnen? Ich bin da leider etwas verwirrt und das vorherige Argument identischer Einzelmessungen passt hier ja nicht.  |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 17. Feb 2016 11:20 Titel: jh8979 Verfasst am: 17. Feb 2016 11:20 Titel: |
 |
|
| FehlerGast hat Folgendes geschrieben: |
Angenommen meine Verteilung ist sehr eng und das Ergebnis meiner Messung lautet (10 +/- 1) µm und mein/e Auflösung/Maßstab erlaubt mir aber nur auf 1 µm genau zu messen, |
Wenn Deine Auflösung nur 1µm ist und Deine Ergebnisse Dir (10 +/- 1) µm, dann heisst das, dass Deine Messung limitiert ist durch Dein Ausloesevermoegen und dass der Fehler +-1µm nicht die "tatsächliche" Standardabweichung der Normalverteilung ist. |
|
 |
FehlerGast
Gast
|
 FehlerGast Verfasst am: 18. Feb 2016 09:56 Titel: FehlerGast Verfasst am: 18. Feb 2016 09:56 Titel: |
 |
|
Danke, für deine Antwort!
Deiner Betrachtung zufolge müsste die Standardabweichung meinen Fehler also schon enthalten. Irgendwie habe ich trotzdem noch Probleme damit. Zum einen ist es ja so, dass mein Fehler zufällig ist. Ich messe also bei manchen Partikeln 1µm zu viel, bei manchen 1µm zu wenig. Statistisch gesehen, können sich da ja die Fehler und die wahren Größenunterschiede kompensieren. Ich kann also mal bei einem 9 µm Partikel 1µm zu viel messen und bei einem 11µm Partikel 1µm zu wenig. Beide Partikel würde ich also mit einem Durchmesser von  10 µm angeben. Mein Mittelwert würde sich nicht ändern, aber die Standardabweichung macht es doch kleiner, oder? 10 µm angeben. Mein Mittelwert würde sich nicht ändern, aber die Standardabweichung macht es doch kleiner, oder?  Im ungüsntigsten Fall passiert das in 50% der Fälle, wenn ich sehr viele Partikel vermesse. Dann wäre meine Standardabweichung Im ungüsntigsten Fall passiert das in 50% der Fälle, wenn ich sehr viele Partikel vermesse. Dann wäre meine Standardabweichung 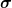 der Verteilung auf Grund des Messfehlers kleiner, als sie tatsächlich ist. Müsste ich dann nicht also doch die Standardabweichung und den Messfehler quadratisch aufaddieren, um eine gute Abschätzung für die reale Verteilung zu bekommen? Also: der Verteilung auf Grund des Messfehlers kleiner, als sie tatsächlich ist. Müsste ich dann nicht also doch die Standardabweichung und den Messfehler quadratisch aufaddieren, um eine gute Abschätzung für die reale Verteilung zu bekommen? Also:
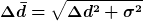
Oder ein anderes Beispiel, mit anderen Zahlenwerten:
Ich messe 100 Partikel. Ihre wahren Durchmesser 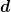 liegen alle zwischen 9,8 µm und 10,2 µm. Messe ich nun mit einer Messauflösung von 0,5 µm, dann kann ich die Werte nie genauer angeben, als 10µm. Ich messe also für alle Partikel 10 µm. Der Mittelwert ist folglich 10 µm, aber die Standardabweichung wäre 0, weil ich alle Partikel zu 10µm bestimmt habe. Trotzdem weiß ich, dass auf Grund meiner Messgenauigkeit, mein Mittelwert liegen alle zwischen 9,8 µm und 10,2 µm. Messe ich nun mit einer Messauflösung von 0,5 µm, dann kann ich die Werte nie genauer angeben, als 10µm. Ich messe also für alle Partikel 10 µm. Der Mittelwert ist folglich 10 µm, aber die Standardabweichung wäre 0, weil ich alle Partikel zu 10µm bestimmt habe. Trotzdem weiß ich, dass auf Grund meiner Messgenauigkeit, mein Mittelwert  maximal auf (10,0 +/- 0,5)µm angegeben werden kann, weil meine Messauflösung halt begrenzt ist. Auch hier gilt dann meiner Ansicht nach, die Summe der Fehlerquadrate gibt eine gute Abschätzung für das Ergebnis: maximal auf (10,0 +/- 0,5)µm angegeben werden kann, weil meine Messauflösung halt begrenzt ist. Auch hier gilt dann meiner Ansicht nach, die Summe der Fehlerquadrate gibt eine gute Abschätzung für das Ergebnis:

Vielleicht hab ich einen Knoten im Kopf, aber irgendwie komme ich bei allen Beispielen, die ich mir ausdenke auf diesen Punkt. Trotzdem bin ich mir nicht ganz sicher, weil ich es eben bei der Wiederholung von Einzelmessungen auch anders machen würde. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 18. Feb 2016 10:54 Titel: jh8979 Verfasst am: 18. Feb 2016 10:54 Titel: |
 |
|
Die Frage ist doch was Du eigentlich messen willst. Wenn Deine Messapparatur ein Ausloesungsvermoegen hat, das in derselben Größenordnung liegt, wie die tatsächliche Standardabweichung in der Größenverteilung, dann ist Dein Experiment einfach schlecht angelegt und Du kannst nicht damit rechnen, die Standardabweichung messen zu können (wie Dein letztes Extrembeispiel schön zeigt).
PS: Die Standardabweichung ist übrigens nicht der Fehler des Mittelwertes... |
|
 |
FehlerGast
Gast
|
 FehlerGast Verfasst am: 18. Feb 2016 13:41 Titel: FehlerGast Verfasst am: 18. Feb 2016 13:41 Titel: |
 |
|
| Zitat: | | Wenn Deine Messapparatur ein Ausloesungsvermoegen hat, das in derselben Größenordnung liegt, wie die tatsächliche Standardabweichung in der Größenverteilung, dann ist Dein Experiment einfach schlecht angelegt und Du kannst nicht damit rechnen, die Standardabweichung messen zu können (wie Dein letztes Extrembeispiel schön zeigt) |
Das ist richtig. Aber mich interessiert eben beides: Mittelwert und die Verteilung um den Mittelwert. Beides möglichst genau. Und es sind ja Situationen vorstellbar, in denen beides in ähnlicher Größenordnung liegt und es nicht genauer geht, weil man eben keine bessere Messaparatur zur Verfügung hat. Dann muss man seine Genauigkeit aber dennoch möglichst gut abschätzen können, um die Aussagekraft seiner Messwerte abschätzen zu können. Das ist ja überhaupt der Sinn der Fehlerbetrachtung. Deswegen meine Frage, wie man dann am sinnvollsten vorgeht.
Und mein Extrembeispiel ist eben der Fall: Die Standardabweichung ist vernachlässigbar klein, gegenüber der Messungenauigkeit. Der andere Extremfall ist: Meine Messungenauigkeit ist vernachlässigbar klein, gegenüber der Standardabweichung. Aber wie gehe ich im Bereich dazwischen vor?
| Zitat: | | PS: Die Standardabweichung ist übrigens nicht der Fehler des Mittelwertes... |
Wenn ich die Standardabweichung von identischen Einzelmessungen mache, dann ja eigentlich schon. Das ist ja auch genau das, was as_string oben auf die ursprüngliche Frage schrieb.
In meinem Beispiel sehe ich das aber auch anders. Da würde ich die Genauigkeit des Mittelwertes auch daran bewerten, wie gut mein Auflösungsvermögen ist und die Standardabweichung dann eben als Verteilung der Stichprobenmesswerte um den Mittelwert betrachten. Dennoch ist da dann eben, wie gesagt, mein Problem: Wie genau ist dann die Standardabweichung und wie gebe ich das alles am besten an? Es gibt ja eigentlich nur die Varianten:
(A) Der Messfehler ist schon in der Standardverteilung enthalten. Dann brauche ich auch den Messfehler / das Auflösungsvermögen angeben.
(B) Der Messfehler ist nicht enthalten. Also muss ich den Wert angeben in der Form: 
(C) Ich fasse meine Auflösung als Ungenauigkeit der Standardabweichung auf und gebe sowas an, wie  mit \Delta{\sigma} = \sqrt{\Delta{\bar{d}}^2 + \Delta{\sigma}^2}. mit \Delta{\sigma} = \sqrt{\Delta{\bar{d}}^2 + \Delta{\sigma}^2}.
Was ist die beste Variante? |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 18. Feb 2016 14:38 Titel: Huggy Verfasst am: 18. Feb 2016 14:38 Titel: |
 |
|
Wenn man es mal rein theoretisch betrachtet, ist die Sache so:
Gegeben sei eine Zufallsgröße Z. Das mögen z. B. die Durchmesser von Schrauben aus einer Fertigungskampagne sein. Es sei bekannt, dass Z normalverteilt ist mit einer Standardabweichung  , die aber noch nicht bekannt ist. , die aber noch nicht bekannt ist.
Nun habe man ein Messverfahren V für Z, von dem ebenfalls bekannt sei, dass es normalverteilte Messwerte mit einer Standardabweichung  liefert. Damit ist gemeint, wenn man wiederholt dieselbe Schraube misst, dann haben die Messwerte dieser Schraube diese Standardabweichung. liefert. Damit ist gemeint, wenn man wiederholt dieselbe Schraube misst, dann haben die Messwerte dieser Schraube diese Standardabweichung.
Wenn man noch annehmen darf, dass die Streuung der Messwerte für eine feste Schraube und die Streuung der wahren Schraubendurchmesser der Fertigungskampagne unabhängig voneinander sind, dann sind die Messwerte M der Zufallsgröße Z mittels des Messverfahrens V ebenfalls eine normalverteilte Zufallsgröße mit einer Standardabweichung

Die so gemessene Streuung der Schraubendurchmesser ist also größer als die wahre Streuung der Schraubendurchmesser. Wenn nun die Streuung  des Messverfahrens bekannt ist, dann kann man mit obiger Beziehung die kleinere tatsächliche Streuung des Messverfahrens bekannt ist, dann kann man mit obiger Beziehung die kleinere tatsächliche Streuung  der Schraubendurchmesser bestimmen. der Schraubendurchmesser bestimmen.
Ich bin kein Praktiker. Aus meiner beruflichen Vergangenheit ist mir allerdings bekannt, dass viele Praktiker dieses Verfahren der Rückrechnung auf die tatsächliche Streung  mit Argwohn betrachten, obwohl es mathematisch einwandfrei ist. Sie akzeptieren aber, dass die tatsächliche Streuung mit Argwohn betrachten, obwohl es mathematisch einwandfrei ist. Sie akzeptieren aber, dass die tatsächliche Streuung  auf jeden Fall kleiner ist als die gemessene Streuung auf jeden Fall kleiner ist als die gemessene Streuung  . . |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 18. Feb 2016 15:17 Titel: jh8979 Verfasst am: 18. Feb 2016 15:17 Titel: |
 |
|
Also, Schritt für Schritt:
Du hast eine Menge Kügelchen und nimmst an, dass deren Größen normalverteilt sind mit einem Mittelwert  und einer Standardabweichung und einer Standardabweichung  . Jetzt misst Du N mal u nd erhaelst irgendwelche Werte . Jetzt misst Du N mal u nd erhaelst irgendwelche Werte 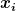 mit Fehlern mit Fehlern  (der Einfachheit halber nehmen wir mal an, die Fehler sind alle gleich und nur der Ablesefehler, und erstmal nehmen wir mal an der wäre klein gegen (der Einfachheit halber nehmen wir mal an, die Fehler sind alle gleich und nur der Ablesefehler, und erstmal nehmen wir mal an der wäre klein gegen  ). ).
1) Was ist der Wert, der den tatsächlichen Werten am nächsten kommt?
Die Antwort ist der Mittelwert

und die zugehörige Standardabweichung
^2})
Jetzt gibt es zwei Fragen von Interesse:
2a) Was ist der Fehler in diesen Größen, der von den Ablesefehlern  verursacht wird? verursacht wird?
Dafür müssen wir nur einfache Fehlerfortpflanzung machen. Die Ablesefehler sind voneinander unabhängig und wir erhalten (wenn alle Fehler gleich gross sind)

und

(wenn ich mich gerade nicht verrechnet hab im Kopf  ) )
2b) Was ist der statistische Fehler in den Abschätzung der beiden Werte?
Die Antwort ist
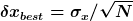
und
} )
und das ist auf jeden Fall größer als der Fehler in (2a), wenn wir annehmen, dass  . .
3) Jetzt betrachten wir was passiert, wenn 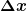 nicht klein ist: Beide Fehler werden kleiner mit mehr Messwerten. Das kann offensichtlich nicht richtig sein, wenn die tatsächliche Standardabweichung nicht klein ist: Beide Fehler werden kleiner mit mehr Messwerten. Das kann offensichtlich nicht richtig sein, wenn die tatsächliche Standardabweichung  sehr viel kleiner ist als unser Ablesefehler sehr viel kleiner ist als unser Ablesefehler 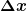 , da dann im Extremfall alle Messungen nur ein-zwei Werte annehmen. Was stimmt also nicht? , da dann im Extremfall alle Messungen nur ein-zwei Werte annehmen. Was stimmt also nicht?
Und die Antwort ist, dass die Abschätzung von  und und  in (2a)offensichtlich nicht gut ist. Denn in diesem Extremfall sind die Fehler nicht unabhängig und wir hätten sie nicht quadratisch addieren sollen, sondern linear. Dann wäre in (2a)offensichtlich nicht gut ist. Denn in diesem Extremfall sind die Fehler nicht unabhängig und wir hätten sie nicht quadratisch addieren sollen, sondern linear. Dann wäre

und
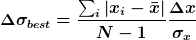
Das lineare addieren der Fehler ist immer der worst case, daher sollten wir hier auf der sicheren Seite sein. Dieser Fehler wird auch immer größer sein als der in (2b).
4) Nachdem wir all das gemacht haben, sollten wir mal überlegen, ob es eigentlich Sinn macht, was wir gemacht haben. Und für den Fall dass die Ablesefehler von derselben Größenordnung sind wie die tatsächliche Standardabweichung ist die Antwort vermutlich: Nein.
In diesem Fall krieg ich nämlich immer nur sehr wenige verschiedene Messwerte, von denen ich garantiert nicht annehmen sollte dass sie normalverteilt sind. Hier macht es wahrscheinlich mehr Sinn einen chi-Quadrattest mit den wenigen möglichen Messwerten als Bins zu machen und zu testen, ob sie jeweils soviel Messpunkte enthalten, wie einer Normalverteilung mit einem bestimmten Mittelwert und einer bestimmten Standardabweichung entsprechen.
5) Was lernen wir daraus?
Fehlerrechnung ist kein Hexenwerk, sondern einfach logischen Verstand einsetzen. Aber sie ist alles andere als eindeutig, daher sollte man immer angeben was genau man meint wenn man schreibt dass eine Messung einen Fehler von +- ... hat. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 18. Feb 2016 15:21 Titel: jh8979 Verfasst am: 18. Feb 2016 15:21 Titel: |
 |
|
|
PS: Ich empfehle übrigens "'An Introduction to Error Analysis - The Study of Uncertainties in Physical Measurements" von John Taylor as Lektuere. Das Buch ist zwar sehr, sehr Basic (geschrieben für Studenten ganz zu Beginn des Studiums), aber sehr klar und verständlich geschrieben. |
|
 |
FehlerGast
Gast
|
 FehlerGast Verfasst am: 28. Feb 2016 12:31 Titel: FehlerGast Verfasst am: 28. Feb 2016 12:31 Titel: |
 |
|
Danke für eure ausführlichen Antworten. Leider bin ich mir innerlich immer noch unsicher, weil es mir auch so scheint, als würden eure Antworten jeweils in entgegengesetzte Richtungen laufen. Zumindest für den Fall, dass die Messungenauigkeit eine Rolle spielt. Ich fasse mal kurz eure Nomenklatur zusammen. Es gilt:
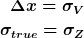
Prinzipiell sagt Huggy's Antwort irgendwie aus, was ich auch die ganze Zeit - etwas diffuser - im Kopf hatte. Also, dass die zufälligen Fehler meines Messverfahrens in der Standardabweichung der Messung enthalten sind. Sowohl für Huggy's, als auch für jh8979's Antwort gilt: Wenn die Messungenauigkeit viel kleiner, als die Standardabweichung der Verteilung ist, dann ist 
Für den Fall, dass die Messungenauigkeit nicht vernachlässigter ist, gilt das dann aber nicht.
Laut Huggy's Ansatz könnte ich die wahre Verteilung dann berechnen oder aber zumindest davon ausgehen, dass mein Messfehler enthalten ist und ich ihn nicht separat angeben muss.
Laut jh8979's Ansatz dürfte ich Huggy's Verfahren aber nicht anwenden, weil die Zufallsgröße M nicht normalverteilt ist. Für mein Extrembeispiel sehe ich das auch ein. Aber sind nicht dennoch genauso gut Fälle vorstellbar, in denen die Größe M, Z und V alle normalverteilt sind und die Standardabweichung von V nicht vernachlässigbar ist? Wenn dieser Fall nicht denkbar ist, dann leuchtet mir leider noch nicht ein warum nicht?
PS: Danke für die Buchempfehlung, jh8979. Aber tatsächlich lese ich das Buch derzeit schon. Ich bin aber erst in Kapitel 5 und bis dahin wurde meine Frage noch nicht geklärt.  |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 29. Feb 2016 12:54 Titel: jh8979 Verfasst am: 29. Feb 2016 12:54 Titel: |
 |
|
| FehlerGast hat Folgendes geschrieben: |
Laut jh8979's Ansatz dürfte ich Huggy's Verfahren aber nicht anwenden, weil die Zufallsgröße M nicht normalverteilt ist. |
Richtig. Dieses Zusammenfassen der Standardabweichungen geht natürlich nur, wenn beide Größen wirklich normalverteilt sind. Ob das wirklich der Fall ist (zumindest in ausreichender Näherung), musst Du von Fall zu Fall entscheiden. Ein guter Test wäre z.B. ob M normalverteilt wäre, wenn die "wahre" Größe, die Du messen willst, einen exakten "wahren" Wert hätte.
| Zitat: | Aber sind nicht dennoch
genauso gut Fälle vorstellbar, in denen die Größe M, Z und V alle normalverteilt sind und die Standardabweichung von V nicht vernachlässigbar ist? |
Sicherlich. Dann gilt ja auch Huggys Formel.
| Zitat: |
PS: Danke für die Buchempfehlung, jh8979. Aber tatsächlich lese ich das Buch derzeit schon. Ich bin aber erst in Kapitel 5 und bis dahin wurde meine Frage noch nicht geklärt.  |
Exakt Dein Fall, tritt in dem Buch auch nicht auf. Allerdings solltest Du nach der Lektüre etwas das Gefühl kriegen, wie man den Fehler behandeln kann/könnte/sollte/... und wie nicht.
PS: Aus reiner Neugier: Wie gefällt Dir das Buch? |
|
 |
Huggy
Anmeldungsdatum: 16.08.2012
Beiträge: 785
|
 Huggy Verfasst am: 29. Feb 2016 13:43 Titel: Huggy Verfasst am: 29. Feb 2016 13:43 Titel: |
 |
|
Das Additionsgesetz für die Varianz einer Summe von Zufallsgrößen gilt für beliebige Verteilungen. Allgemein lautet es:
=Var(X)+Var(Y)+2Cov(X,Y))
Sind die Zufallsgrößen unabhängig, dann ist die Kovarianz 0. Wenn keine Normalverteilungen vorliegen, ist allerdings der Nutzwert des Gesetzes eingeschränkt. Denn dann ist der Anteil der Verteilung, der z. B. im Intervall  liegt, ein anderer als bei der Normalverteilung und hängt von der Art der Verteilung ab. Deshalb hatte ich mich oben auf Normalverteilungen beschränkt. liegt, ein anderer als bei der Normalverteilung und hängt von der Art der Verteilung ab. Deshalb hatte ich mich oben auf Normalverteilungen beschränkt. |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8582
|
 jh8979 Verfasst am: 29. Feb 2016 15:24 Titel: jh8979 Verfasst am: 29. Feb 2016 15:24 Titel: |
 |
|
| Huggy hat Folgendes geschrieben: | Das Additionsgesetz für die Varianz einer Summe von Zufallsgrößen gilt für beliebige Verteilungen. Allgemein lautet es:
=Var(X)+Var(Y)+2Cov(X,Y))
...
Deshalb hatte ich mich oben auf Normalverteilungen beschränkt. |
 |
|
 |
FehlerGast
Gast
|
 FehlerGast Verfasst am: 10. März 2016 13:14 Titel: FehlerGast Verfasst am: 10. März 2016 13:14 Titel: |
 |
|
Vielen Dank euch beiden. Ich denke, nun ist meine Frage beantwortet. 
@jh8979: Das Buch gefällt mir bisher ganz gut. Mittlerweile bin ich auch in Kapitel 10 angekommen. Es ist klar geschrieben, gibt viele Beispiele und obwohl es wie gesagt eher für Erstsemester geschrieben ist, kann man aus der einfachen Argumentationsstruktur die der Autor bereitstellt, viel mitnehmen. Würde das Buch auch jedem weiterempfehlen!  |
|
 |
|
|

















 )
)



