| Autor |
Nachricht |
macman2010
Anmeldungsdatum: 16.02.2013
Beiträge: 294
|
 macman2010 Verfasst am: 23. Mai 2013 21:45 Titel: Kondensator lädt Kondensator. |
 |
|
Hallo.
Folgendes.
Zwei Kondensatoren einer 1F der andere 0,5F
Der 1ner hat eine Spannung von 10V Intus.
Der 0,5er ist Leer.
So wie ist die spannung am Ende, wenn man die Zusammenhängt. Natürlich ohne weitere Spannungsquelle.
Meine Rechnung ordentlich mit LAtex.
Das war ja einfach.. Aber jetzt kommt der Eigentliche hammer, den ich mich Frage.
Was passiert, wenn da in der Mitte jetzt ein Widerstand von 100Ohm ruht.
Ich habe mir alle Möglichen Gleichungen Ausgedacht, aber keine Dieser brachte mich bis jetzt zum Ziel :-(
Einen Kandidaten, kann ich ja Mal Präsentieren. (Zeichnung spare ich mir an dieser Stelle, glaube jeder Kann sich das Vorstellen.)
\; +\; \left( Ladungsmenge\; die\; an\; R\; Verlo\mbox{re}n\; ging!! \right))
Denke das Grundgerüst stimmt aber dieser Term für R wäre mir Wichtig..
Thanks
|
|
 |
Klondijk457
Gast
|
| Klondijk457 Verfasst am: 23. Mai 2013 21:52 Titel: |
|
|
Wohin sollte denn Ladung verloren gehen?!
Im Stau verschwinden ja auch keine Autos..
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 23. Mai 2013 22:55 Titel: |
|
|
| Klondijk457 hat Folgendes geschrieben: | | Wohin sollte denn Ladung verloren gehen?! |
Was da verloren geht, ist natürlich keine Ladung sondern Energie.
|
|
|
D2
Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
| D2 Verfasst am: 23. Mai 2013 23:27 Titel: |
|
|
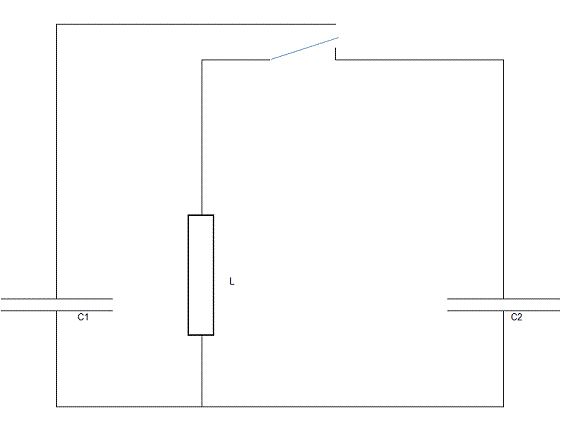
Wieviel Energie geht verloren wenn man
über eine Induktivität L anstatt einen Widerstand
Kondensator C1 vollständig an C2 entladet?
Wie hoch wird die Spannung an C2 in günstigsten Fall sein?
Zwei Kondensatoren einer C1 =1F der andere C2 = 0,5F
Der 1ner hat eine Spannung von 10V Intus.
Der 0,5er ist Leer.
| Beschreibung: |
|
| Dateigröße: |
4.88 KB |
| Angeschaut: |
8317 mal |
|
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 24. Mai 2013 03:08 Titel: |
|
|
@D2
Wärest Du so freundlich, Dich erstmal auf die Fragestellung von macman2010 zu konzentrieren? Deine Abschweifung vom Thema hilft ihm nämlich überhaupt nicht.
Falls Deine Frage ernst gemeint ist, d.h. falls Du sie wirklich beantwortet oder diskutiert haben willst, dann mach bitte einen eigenen Thread auf.
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 24. Mai 2013 03:43 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | Klondijk457 hat Folgendes geschrieben: | | Wohin sollte denn Ladung verloren gehen?! |
Was da verloren geht, ist natürlich keine Ladung sondern Energie. |
... wobei die "verloren" gegangene Energie unabhängig von der Größe des Widerstandes ist.
|
|
|
Klondijk457
Gast
|
| Klondijk457 Verfasst am: 24. Mai 2013 03:45 Titel: |
|
|
| Zitat: | | Deine Abschweifung vom Thema hilft ihm nämlich überhaupt nicht. |
Deine auch nicht!
Und seine passen immerhin besser zum Thema.
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 24. Mai 2013 04:16 Titel: |
|
|
| Klondijk457 hat Folgendes geschrieben: | | Zitat: | | Deine Abschweifung vom Thema hilft ihm nämlich überhaupt nicht. |
Deine auch nicht!
Und seine passen immerhin besser zum Thema. |
Ach ja? macman2010 will eine Kondensatorumladung über einen Widerstand besprechen, D2 eine Umladung über eine Induktivität. Und das auch noch mit einer Schaltung, die dafür nicht geeignet ist. Sollten wir nicht besser bei dem von macman2010 vorgegebenen Szenario bleiben? Ich bin jedenfalls dabei geblieben, DrStupid ebenfalls, Du auch, D2 nicht.
|
|
|
macman2010
Anmeldungsdatum: 16.02.2013
Beiträge: 294
|
| macman2010 Verfasst am: 24. Mai 2013 15:47 Titel: |
|
|
Die verlorengehende Energie sind meine ich 50% wenn ich mich nicht irre.
Kommt mir aber auch irgendwo komisch vor, denn das würde ja heißen, dass ein Kondensator höchsten Wirkungsgrad 0.5 bzw. 50% ist.
Das kommt mir komisch vor.
Rechnen könnte ich das doch integral(R•(ladestromfunktion für Strom)•t)dt
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 24. Mai 2013 17:10 Titel: |
|
|
| macman2010 hat Folgendes geschrieben: | | Die verlorengehende Energie sind meine ich 50% wenn ich mich nicht irre. |
Ich weiß zwar nicht, was Deine 50% sind, aber ein Energie"verlust" (tatsächlich ist es die Energie, die bei der Umladung als Wärme- bzw. Strahlungsenergie abgegeben wird) von 50% ergibt sich nur, wenn beide Kondensatoren gleiche Kapazität haben. Das ist in Deiner Aufgabe aber nicht der Fall.
| macman2010 hat Folgendes geschrieben: | Kommt mir aber auch irgendwo komisch vor, denn das würde ja heißen, dass ein Kondensator höchsten Wirkungsgrad 0.5 bzw. 50% ist.
Das kommt mir komisch vor.
|
Wie definierst Du denn den Wirkungsgrad eines Kondensators?
| macman2010 hat Folgendes geschrieben: | | Rechnen könnte ich das doch integral(R•(ladestromfunktion für Strom)•t)dt |
Nein mit Sicherheit nicht. Das stimmt ja dimensionsmäßig überhaupt nicht. Da bekämest Du eine Grö0e mit der Einheit Vs² raus. Was soll das denn sein? Wenn Du die im Widerstand umgesetzte Energie tatsächlich über ein Integral berechnen willst, dann muss das lauten
^2\, dt)
Einfacher ist es, eine Energiebilanz der elektrischen Feldenergie aufzustellen, dann ist
\cdot U_2^2))
mit
Wenn Du das einsetzt, erhältst Du
)
Für Deine ursprüngliche Beispielaufgabe wäre dann der Energie"verlust" ein Drittel der Anfangsenergie. Und der ist, nebenbei bemerkt, völlig unabhängig von der Größe des Widerstandes R, wie man sieht, sondern nur abhängig von der Größe der beiden Kondensatoren.
|
|
|
macman2010
Anmeldungsdatum: 16.02.2013
Beiträge: 294
|
| macman2010 Verfasst am: 24. Mai 2013 17:31 Titel: |
|
|
Sorry ich wollte da dt schreiben statt t
Bei deiner energiebilanz wie kommst du da auf 1/2
Noch so nebenbei wenn man von einer idealen Kapazität ausgeht, geht ja keine Energie verloren und diese Formel kann nicht stimmen.
Da fällt mir gerade noch auf die integrationsgrenzen kannst du doch nicht ernst meinen...
|
|
|
Klondijk457
Gast
|
| Klondijk457 Verfasst am: 24. Mai 2013 17:45 Titel: |
|
|
Oder du schaust einfach welche Energie vorher drin steckte und welche nachher noch vorhanden ist. Die zeitliche Entwicklung spielt keine Rolle.
Wenn ein Kondensator leer ist, hängt der Wirkungsgrad nur von den Kapazitäten ab, kann also von 0% bis 100% reichen.. Die Rechnung dazu ist wirklich kurz. Also...
@GvC:
Ich hatte nicht gesehen, dass du im selben Moment geschrieben hast, und hatte mich darum nur auf deinen ersten Beitrag bezogen. Denn mal davon abgesehen, dass der Text und das Bild nicht zusammen passen, hat seine Idee schon etwas hiermit zu tun, da ja nicht nur die Größe sondern auch die Art des Widerstandes keinen Einfluss auf die Energiebilanz nehmen.
| Zitat: | | Und das auch noch mit einer Schaltung, die dafür nicht geeignet ist. |
Na also, jetzt hast du ihm doch noch geholfen. Ist doch besser als ihn nur tadeln zu wollen.. Allerdings würde ich auch sagen, dass eine neue Frage in einen neuen Beitrag gehört. Aber wenn wir schon dabei sind..
@D2:
Um mal beim Ausgangsszenario zu bleiben: Vollständig entladen kann man einen Kondensator nicht mit einem anderen. Der Vorgang geht nur so weit bis sich beide Spannungen angeglichen haben.
Schwingkreise etc. sind da wirklich ein anderes Thema.
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 24. Mai 2013 17:49 Titel: |
|
|
| macman2010 hat Folgendes geschrieben: | | Sorry ich wollte da dt schreiben statt t |
Dann wäre es immer noch nicht richtig. Der Strom muss quadriert werden, denn P=R*I².
| macman2010 hat Folgendes geschrieben: | | Bei deiner energiebilanz wie kommst du da auf 1/2 |
Ich komme nirgendwo auf 1/2, sondern
| GvC hat Folgendes geschrieben: | | Für Deine ursprüngliche Beispielaufgabe wäre dann der Energie"verlust" ein Drittel der Anfangsenergie. |
| macman2010 hat Folgendes geschrieben: | | Noch so nebenbei wenn man von einer idealen Kapazität ausgeht, geht ja keine Energie verloren und diese Formel kann nicht stimmen. |
Das ist eine abenteuerliche Behauptung. Was ist falsch daran, die in den Kondensatoren vorher und nachher gespeicherte Energie zu berechnen und ihre Differenz zu bilden? Und diese Rechnung zeigt Dir, dass Energie "verloren" gehen muss (außer wenn C2=0, dann findet aber auch keine Umladung statt). Die Behauptung, dass bei idealen Kondensatoren bei der Umladung keine Energie verloren geht, ist durch kein einziges physikalisches Grundgesetz zu begründen. (Tatsächlich geht sie ja auch nicht verloren, sondern wird in eine andere Energieform umgewandelt (Energieerhaltungssatz), aber als in den Kondensatoren gespeicherte Energie ist sie nicht mehr vorhanden.)
|
|
|
Klondijk457
Gast
|
| Klondijk457 Verfasst am: 24. Mai 2013 18:53 Titel: |
|
|
| Zitat: | | Was ist falsch daran, die in den Kondensatoren vorher und nachher gespeicherte Energie zu berechnen und ihre Differenz zu bilden? ... |
Sagte ich doch schon... 
Schon erstaunlich, wie zeitnah wir immer etwas schreiben...
@macman2010:
Ich denke was dich verwirrt, ist, dass du andere Energieformen nicht explizit berücksichtigt hast, stimmt's?
Aber das steckt sozusagen schon in der Kondensatorenergie mit drin. Vielleicht wird das deutlicher, wenn du dir einfach den Verlauf der gespeicherten Energie beim Kurzschluss eines geladenen Kondensators vorstellst. Dabei ist ebensowenig von anderen Energien die Rede, dennoch nimmt sie ab.
Darum kann man hier ruhig von verlorener Energie (ohne "") sprechen, da es immer auf das betrachtete System ankommt!
|
|
|
D2
Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
| D2 Verfasst am: 24. Mai 2013 19:02 Titel: |
|
|
Hallo Leute,
es tut mir leid dass ich mich mit meiner Zeichnung eingemischt habe,
aber mich hat gestört, dass die gespeicherte Energie verloren gehen oder Art des Widerstandes keine Rolle spielen soll.
Erhaltungssätze darf man nicht verletzen und 2 Kondensatoren umzuladen, nur dann zu kleineren Verlusten führt, wenn Kondensator der lädt möglichst hohe und der der lädt, niedrige Kapazität hat.
Anstatt Hilfswiderstand R eine Diode, Induktivität oder weitere Kondensatoren zu verwenden(andere Arten von Widerständen) ändert Ladevorgang und führt zu interessanten Erkentnissen.
Ich dachte "macman2010" hat Interesse zu erfahren wie man elektrische Energie mit möglich kleinen Verlusten von einem Kondensator in den anderen
überführen kann. Da er R erwähnt hat, sah ich die Möglichkeit zu zeigen, dass man den Energieverlust nicht unbedingt in Kauf nehmen muss.
Es geht natürlich nicht um ideale Kondensatoren, die helfen ihm auch nicht.
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 24. Mai 2013 19:30 Titel: |
|
|
| GvC hat Folgendes geschrieben: | Wenn Du die im Widerstand umgesetzte Energie tatsächlich über ein Integral berechnen willst, dann muss das lauten
|
Da ich gerade nichts besseres zu tun hatte, habe ich das mal durchgerechnet. Weil über den Kondensatoren während der Umladung ungleiche Spannungen abfallen, habe ich die Ladungsbilanz erst einmal etwas umformuliert:
Damit haben die Indizes in meiner Rechnung eine andere Bedeutung als in der bisherigen Diskussion, aber ich denke es wird hinreichend klar, was gemeint ist. Daraus folgt dann schon mal
 \cdot \frac{{C_1 }}{{C_2 }})
Die Spannung des zweiten Kondensators hängt also explizit von der des ersten ab womit ich meine Rechnung auf einen von beiden beschränken kann. Für die Änderung der Spannung gilt
Die Stromstärke ergibt sich aus dem Widerstand und der darüber abfallenden Spannung:
mit
Alles zusammen ergibt die Differentialgleichung
)
und mittels Variation der Konstanten erhalte ich die Lösung
} \right]} \right\})
und somit auch
} \right]} \right\})
Damit kann ich mich endlich der Wärmeentwicklung zuwenden:
Mit den obigen Gleichungen ergibt das
} \right])
und die Integration liefert
} \right]} \right\})
Jetzt muss ich nur noch ausrechnen was im Unendlichen passiert:
| GvC hat Folgendes geschrieben: | | Einfacher ist es, eine Energiebilanz der elektrischen Feldenergie aufzustellen |
Warum einfach, wenns auch kompliziert geht?
|
|
|
macman2010
Anmeldungsdatum: 16.02.2013
Beiträge: 294
|
| macman2010 Verfasst am: 24. Mai 2013 19:40 Titel: |
|
|
|
wofür lim wen interessiert das??
|
|
|
Namenloser324
Gast
|
| Namenloser324 Verfasst am: 24. Mai 2013 19:41 Titel: |
|
|
| D2 hat Folgendes geschrieben: | Hallo Leute,
es tut mir leid dass ich mich mit meiner Zeichnung eingemischt habe,
aber mich hat gestört, dass die gespeicherte Energie verloren gehen oder Art des Widerstandes keine Rolle spielen soll.
Erhaltungssätze darf man nicht verletzen und 2 Kondensatoren umzuladen, nur dann zu kleineren Verlusten führt, wenn Kondensator der lädt möglichst hohe und der der lädt, niedrige Kapazität hat.
Anstatt Hilfswiderstand R eine Diode, Induktivität oder weitere Kondensatoren zu verwenden(andere Arten von Widerständen) ändert Ladevorgang und führt zu interessanten Erkentnissen.
Ich dachte "macman2010" hat Interesse zu erfahren wie man elektrische Energie mit möglich kleinen Verlusten von einem Kondensator in den anderen
überführen kann. Da er R erwähnt hat, sah ich die Möglichkeit zu zeigen, dass man den Energieverlust nicht unbedingt in Kauf nehmen muss.
Es geht natürlich nicht um ideale Kondensatoren, die helfen ihm auch nicht. |
Jemand der hier postet hat meist eine konkrete Frage auf die er sich konkrete Hilfe oder konkrete Lösungsansätze erhofft.
Dein Einwurf ist fern ab davon und eröffnet wiederum eine ganz andere Fragestellung und ist deshalb fehl am Platz.
|
|
|
macman2010
Anmeldungsdatum: 16.02.2013
Beiträge: 294
|
| macman2010 Verfasst am: 24. Mai 2013 19:45 Titel: |
|
|
| GvC hat Folgendes geschrieben: | | macman2010 hat Folgendes geschrieben: | | Die verlorengehende Energie sind meine ich 50% wenn ich mich nicht irre. |
Ich weiß zwar nicht, was Deine 50% sind, aber ein Energie"verlust" (tatsächlich ist es die Energie, die bei der Umladung als Wärme- bzw. Strahlungsenergie abgegeben wird) von 50% ergibt sich nur, wenn beide Kondensatoren gleiche Kapazität haben. Das ist in Deiner Aufgabe aber nicht der Fall.
| macman2010 hat Folgendes geschrieben: | Kommt mir aber auch irgendwo komisch vor, denn das würde ja heißen, dass ein Kondensator höchsten Wirkungsgrad 0.5 bzw. 50% ist.
Das kommt mir komisch vor.
|
Wie definierst Du denn den Wirkungsgrad eines Kondensators?
| macman2010 hat Folgendes geschrieben: | | Rechnen könnte ich das doch integral(R•(ladestromfunktion für Strom)•t)dt |
Nein mit Sicherheit nicht. Das stimmt ja dimensionsmäßig überhaupt nicht. Da bekämest Du eine Grö0e mit der Einheit Vs² raus. Was soll das denn sein? Wenn Du die im Widerstand umgesetzte Energie tatsächlich über ein Integral berechnen willst, dann muss das lauten
Einfacher ist es, eine Energiebilanz der elektrischen Feldenergie aufzustellen, dann ist
mit
Wenn Du das einsetzt, erhältst Du
Für Deine ursprüngliche Beispielaufgabe wäre dann der Energie"verlust" ein Drittel der Anfangsenergie. Und der ist, nebenbei bemerkt, völlig unabhängig von der Größe des Widerstandes R, wie man sieht, sondern nur abhängig von der Größe der beiden Kondensatoren. |
nein du hast natürlich in deiner rechnung nirgends 1/2 stehen wie komme ich bloß dadrauf... Spass beiseite.
Dieser rechenschritt
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 24. Mai 2013 20:16 Titel: |
|
|
| macman2010 hat Folgendes geschrieben: | | wofür lim |
Um zu sehen, was am Ende raus kommt.
| macman2010 hat Folgendes geschrieben: | | wen interessiert das?? |
Alle die am Ergebnis interessiert sind.
|
|
|
D2
Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
| D2 Verfasst am: 24. Mai 2013 20:26 Titel: |
|
|
Lim Q ist nicht richtig, bitte korrigieren, da muss Lim W stehen
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
|
macman2010
Anmeldungsdatum: 16.02.2013
Beiträge: 294
|
| macman2010 Verfasst am: 24. Mai 2013 20:32 Titel: |
|
|
| GvC hat Folgendes geschrieben: | | macman2010 hat Folgendes geschrieben: | | Die verlorengehende Energie sind meine ich 50% wenn ich mich nicht irre. |
Ich weiß zwar nicht, was Deine 50% sind, aber ein Energie"verlust" (tatsächlich ist es die Energie, die bei der Umladung als Wärme- bzw. Strahlungsenergie abgegeben wird) von 50% ergibt sich nur, wenn beide Kondensatoren gleiche Kapazität haben. Das ist in Deiner Aufgabe aber nicht der Fall.
| macman2010 hat Folgendes geschrieben: | Kommt mir aber auch irgendwo komisch vor, denn das würde ja heißen, dass ein Kondensator höchsten Wirkungsgrad 0.5 bzw. 50% ist.
Das kommt mir komisch vor.
|
Wie definierst Du denn den Wirkungsgrad eines Kondensators?
| macman2010 hat Folgendes geschrieben: | | Rechnen könnte ich das doch integral(R•(ladestromfunktion für Strom)•t)dt |
Nein mit Sicherheit nicht. Das stimmt ja dimensionsmäßig überhaupt nicht. Da bekämest Du eine Grö0e mit der Einheit Vs² raus. Was soll das denn sein? Wenn Du die im Widerstand umgesetzte Energie tatsächlich über ein Integral berechnen willst, dann muss das lauten
Einfacher ist es, eine Energiebilanz der elektrischen Feldenergie aufzustellen, dann ist
mit
Wenn Du das einsetzt, erhältst Du
Für Deine ursprüngliche Beispielaufgabe wäre dann der Energie"verlust" ein Drittel der Anfangsenergie. Und der ist, nebenbei bemerkt, völlig unabhängig von der Größe des Widerstandes R, wie man sieht, sondern nur abhängig von der Größe der beiden Kondensatoren. |
Wo geht diese Energielieferung aber hin, wenn die Kapazität Ideal ist?? Die Leitungen ebenso. Wärme ist dann ja unmöglich.
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 24. Mai 2013 20:50 Titel: |
|
|
| D2 hat Folgendes geschrieben: | | Lim Q ist nicht richtig, bitte korrigieren, da muss Lim W stehen |
W wird normalerweise für die Arbeit verwendet. Der Widerstand leistet aber keine Arbeit, sondern er produziert Wärme und für die ist das Formelzeichen Q üblich.
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 24. Mai 2013 20:52 Titel: |
|
|
| macman2010 hat Folgendes geschrieben: | | Wo geht diese Energielieferung aber hin, wenn die Kapazität Ideal ist?? Die Leitungen ebenso. Wärme ist dann ja unmöglich. |
In dem Fall gibt es wohl einen EMP.
|
|
|
D2
Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
| D2 Verfasst am: 24. Mai 2013 20:55 Titel: |
|
|
| macman2010 hat Folgendes geschrieben: | | Wo geht diese Energielieferung aber hin, wenn die Kapazität Ideal ist?? Die Leitungen ebenso. Wärme ist dann ja unmöglich. |
W alt= Q² / 2*C1 ; Ladung kann nicht verschwinden
Du erhöchst deine Kapazität C neu = C1+C2
W neu = Q² / 2*(C1 +C2)
So sinkt deine Spannung in diesem Fall entsprechend.
So hast du die elektrische Energie erniedrig.
Die ist im Blitz verschwunden, falls deine Leitungen Null ohmsche Widerstand besitzen sollen.
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
|
macman2010
Anmeldungsdatum: 16.02.2013
Beiträge: 294
|
| macman2010 Verfasst am: 24. Mai 2013 21:31 Titel: |
|
|
wie kommt ihr immer auf diese 1/2 W=U^2*(Cges) ohne 1/2
denn u=const
C=const
|
|
|
D2
Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
|
|
macman2010
Anmeldungsdatum: 16.02.2013
Beiträge: 294
|
| macman2010 Verfasst am: 24. Mai 2013 22:01 Titel: |
|
|
Ich bin jetzt tatsächlich auch auf diese Formel gestoßen.
Aber ich hatte mal in der schule mal gelernt Q*U=W
warum darf man das hier jetzt nicht auch einfach so rechnen.
Denn in einer Batterie ists ja auch Q*U=W
W = ∫U(q)dq
|
|
|
D2
Anmeldungsdatum: 10.01.2012
Beiträge: 1723
|
| D2 Verfasst am: 24. Mai 2013 22:09 Titel: |
|
|
Die Fläche ist der Weg.
Wir haben die Hälfte des Rechtecks rot gezeichnet.
| Beschreibung: |
|
Download |
| Dateiname: |
EnergieKond2.gif |
| Dateigröße: |
79.29 KB |
| Heruntergeladen: |
1159 mal |
_________________
Lösungen gibt es immer, man muss nur darauf kommen. |
|
|
Klondijk457
Gast
|
| Klondijk457 Verfasst am: 24. Mai 2013 22:14 Titel: |
|
|
Das steht doch sogar da im TEXT!!!     
Sinkt bei einer Batterie die Spannung proportional zur Ladungsentnahmen?!
(Sinkt sie idealerweise überhaupt?!!)
Ist sie also überhaupt ein Kondensator?!
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 24. Mai 2013 22:26 Titel: |
|
|
| macman2010 hat Folgendes geschrieben: |
Aber ich hatte mal in der schule mal gelernt Q*U=W
warum darf man das hier jetzt nicht auch einfach so rechnen.
Denn in einer Batterie ists ja auch Q*U=W |
Um so rechnen zu können, muss die Spannung konstant sein. Bei einer Batterie kann man das mit ruhigem Gewissen annehmen, bei einem Kondensator dagegen nicht.
| macman2010 hat Folgendes geschrieben: | | W = ∫U(q)dq |
 = \frac{q}{C})
|
|
|
macman2010
Anmeldungsdatum: 16.02.2013
Beiträge: 294
|
| macman2010 Verfasst am: 25. Mai 2013 12:41 Titel: |
|
|
Danke..
Hab da noch ne frage, vielleicht sollte ich einen neuen Tread aufmachen. Aber ich Versuchs erstmal hier.
Mit meinen 50 Prozent Verlust habe ich vorhin mit dem Landesvorgang an konstanter Spannung verwechselt.
Bei einer Ladung an konstanter Spannung gehen ja immer 50% Flöten.
Warum ist das dann z.b. Bei pulsierender Gleichspannung wo der Kondensator
Als glättung dient nicht so.
Liegt das rein ander Kurve?? Denn Strom ist ja c*du/dt
Bei einem brückengleichrichter wäre das dann ja |û*sin(wt)|'*c
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 25. Mai 2013 12:59 Titel: |
|
|
|
Nein, beim Glättungskondensator folgt der Kondensatorstrom nicht dem Sinus- bzw. Kosinusverlauf der Spannung. Der Kondenstor wird einmal auf den Maximalwert aufgeladen. Dabei geht natürlich Energie als Wärme verloren, denn der Ladestrom fließt durch den Zuleitungswiderstand zum Kondensator. Sobald die Spannung entsprechend der Sinusform absinkt, müsste laut i=C*du/dt der Strom negativ werden, das wird aber durch die Gleichrichterschaltung verhindert. Der Kondensator bleibt also prinzipiell aufgeladen und entlädt sich nur mehr oder weniger geringfügig über den Lastwiderstand, muss also immer wieder mehr oder weniger nachgeladen werden, wobei wiederum Wärmeverluste entstehen. Wenn die Kapazität des Kondensators groß genug ist, ist die bei der Ent- und Nachladung entstehende Spannungsschwankung nur noch als ganz kleiner "ripple" zu erkennen. Deshalb nennt sich ein solcher Kondensator ja auch Glättungskondensator.
|
|
|
macman2010
Anmeldungsdatum: 16.02.2013
Beiträge: 294
|
| macman2010 Verfasst am: 25. Mai 2013 14:59 Titel: |
|
|
Glaube du hast ein klein wenig falsch Verstanden was ich meine.
Ein kondensator an konstanter spannungsquelle lädt sich ja nach einer e-Funktion egal mit welchem widerstand kommt nur die Hälfte der Energie im Feld des Kondensators an.
Also Wirkungsgrad 50%
Wenn das bei einem Gleichrichter so wäre, wäre das ja furchtbar.
Der kondensator folgt doch aber beim aufladen dem Sinus Betrag.
Und schon ist der Wirkungsgrad besser oder was meinst du??
|
|
|
macman2010
Anmeldungsdatum: 16.02.2013
Beiträge: 294
|
| macman2010 Verfasst am: 25. Mai 2013 16:28 Titel: |
|
|
|
??
|
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 26. Mai 2013 08:33 Titel: |
|
|
| macman2010 hat Folgendes geschrieben: | | Glaube du hast ein klein wenig falsch Verstanden was ich meine. |
Dann erklär's mir bitte. Zum Beispiel mit einer kleinen Schaltskizze.
|
|
|
macman2010
Anmeldungsdatum: 16.02.2013
Beiträge: 294
|
| macman2010 Verfasst am: 02. Jun 2013 21:14 Titel: |
|
|
Also ok... Bei einem Wechselstrom gehen ja nicht die Hälfte der Energie am Kondensator Flöten... Denn du kannste ja rechnen. Bei 0,1 Ohm innenwiderstand wenn überhaupt und bspw. 500 Ohm Xc verliert der Stromkreis nur wenige Joules pro zeit.
Für mein Modell, gehe ich jetzt davon aus, man im nulldurchgang die Gleichrichter Schaltung einschaltet. Dann ist der Strom ja du/dt der Kondensator, verhält sich sozusagen als blindwiderstand.
Denn, wenn der Kondensator, bei jedem nachladen 50% der Energie verlieren würde, dann würde das ja aufgrund der hohen Verluste niemand machen.
Wahrscheinlich hat der Kondensator Strom im aufladmoment sogar den gleichen phasenwinkel wie bei Wechselstrom.
Aber noch ne andere frage. Wenn der Kondensator einen 100 Ohm widerstand vorsich hätte. Würde er ja im könnte man ja die kondensatorspannung im Scheitelpunkt der Gleichrichter Spannung über den Phasen Winkel berechnen. Wie ist es aber, wenn der Kondensator halb geladen ist, die Spannung dann bei
Der Hälfte die Diode zum leiten bringt. Wie weit, wäre der Kondensator jetzt, wenn der Kondensator seinen Scheitel erreicht, und wann würde die Diode wieder sperren. Sprich wann ist kondensatorspannung und Gleichrichter Spannung gleich??
|
|
|
Za-hef
Anmeldungsdatum: 13.11.2011
Beiträge: 36
|
| Za-hef Verfasst am: 29. Nov 2021 22:24 Titel: |
|
|
Sorry wenn ich den alten Thread wieder ausgrabe. Gehe grad die alternative Lösung von Dr.Stupid durch und stolpere über diesen Schritt:
| DrStupid hat Folgendes geschrieben: |
Damit kann ich mich endlich der Wärmeentwicklung zuwenden:
|
Ich stehe da auf dem Schlauch. Woher kommt das? Die Definition von Strom ist doch:
Deshalb verstehe ich nicht wie die Spannungsdifferenz da reinpasst.
Und noch ein Punkt.
Man könnte ja auch dieses Integral berechnen:
^2\, dt =\int_0^\infty \frac{U(t)^2}{R}\, dt=\int_0^\infty \frac{(U_{1}-U_{2})^2}{R}\, dt)
mit ) als Spannung die über den Widerstand abfällt und  als Lösungen der DGL wie oben erhalten.
Wenn ich da rumrechne komme ich aber auf Quatsch. Verrechne ich mich oder ist der Ansatz Käse?
|
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 30. Nov 2021 14:09 Titel: |
|
|
| Zitat: | Ich stehe da auf dem Schlauch. Woher kommt das? Die Definition von Strom ist doch:
|
Vorsicht, ich glaube DrStupid verwendet für die Wärmeentwicklung das Symbol Q, obwohl dieses in diesem Kontext natürlich eher für die Ladung stehen sollte. Wie man Dinge benennt ist aber letztendlich nebensächlich. dQ/dt ist bei DrStupid die Momentanleistung, d.h. die Wärmeentwicklung in J pro Sekunde.
Diese Art von Aufgabe ist übrigens ein sehr altes "Paradoxon", denn der stabile Zustand kann sich nicht einstellen, ohne dass Energie entnommen wird. Ladungserhaltug und gleichzeitige Energieerhaltung stehen hier nämlich im scheinbaren "Widerspruch".
Der Endzustand hängt jedenfalls nicht von R ab, was man leicht zeigen kann.
Was Du da am Ende gerechnet hast, habe ich mir aber nicht angesehen. Deshalb kann ich dazu auch nichts sagen, aber irgendwo wirst du wohl einen Wurm drin haben ...
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
gast_free
Anmeldungsdatum: 15.07.2021
Beiträge: 195
|
| gast_free Verfasst am: 01. Dez 2021 16:21 Titel: |
|
|
Parallelschaltung:
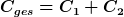
Energieerhaltung:
Parallelschaltung mit Widerstand:
Zeit für 
|
|
|
|
Registrieren
Login
FAQ
Suchen
