| Autor |
Nachricht |
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
 Physinetz Verfasst am: 13. Jan 2010 18:24 Titel: Moment im 3 Dimensionalen berechnen Physinetz Verfasst am: 13. Jan 2010 18:24 Titel: Moment im 3 Dimensionalen berechnen |
 |
|
Hallo zusammen, habe folgendes Problem:
Also erstmal die gesamte Aufgabe im Anhang.
Anschließend freigeschnitten.
Also soweit verstehe ich das alle noch, nur wenn es darum geht neben den Kräftegleichgewichten nun auch noch das Momentengleichgewicht anzusetzen wird es schwer für mich.
Ich verstehe einfach nicht, wie man bei den Momenten in x,y und z Richtung auf die jeweiligen Kräfte kommt, die für die Momente in x,y, und z-Richtung relevant sind.
Also was mir klar ist: Moment=Kraft x Hebelarm.
Also wenn man praktisch nicht über das Vektorprodukt gehen möchte, benötigt man ja immer den senkrechten Anteil und davon den Abstand...
Nur weiß ich leider nicht wieso z.B. für } ) man nur die Kräfte man nur die Kräfte  und und  berücksichtigen muss.Weiß jemand einen Tipp wie man da leicht draufkommt? berücksichtigen muss.Weiß jemand einen Tipp wie man da leicht draufkommt?
Vielen Dank für Eure Hilfe
beste Grüße sagt Physinetz
| Beschreibung: |
|
| Dateigröße: |
11.28 KB |
| Angeschaut: |
37248 mal |
|
| Beschreibung: |
|
| Dateigröße: |
17.81 KB |
| Angeschaut: |
37248 mal |

|
| Beschreibung: |
|

Download |
| Dateiname: |
Leiter.JPG |
| Dateigröße: |
42.74 KB |
| Heruntergeladen: |
8659 mal |
|
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 13. Jan 2010 20:42 Titel: schnudl Verfasst am: 13. Jan 2010 20:42 Titel: |
 |
|
Stelle dir vor, du legst durch B eine (gedachte) Drehachse entlang x.
Das Moment bezüglich dieser Achse ist dann  . .
Welche Kräfte führen nun zu einer (gedachten) Drehung um diese Achse? Was ist die Bedingung dafür? Vielleicht wird dir klar, weshalb die anderen Kräfte dann kein Moment bezüglich dieser Achse erzeugen.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 14. Jan 2010 00:33 Titel: VeryApe Verfasst am: 14. Jan 2010 00:33 Titel: |
 |
|
das kann man sich noch einfacher vorstellen.
Es gibt drei Achsen im dreidimensionalen Raum x,y,z die kennsd du ja.
Trotzdem zeichnen und rechnen wir als Beginner der Mechanik immer nur 2 dimensional als ob die Tiefe im Raum nicht existiert. Das geht dann wenn alle Kräfte immer in einer gemeinsamen Raumebene wirken oder zumindest deren Resultierenden.
Z.B Beispiel ein symmetrischer Sessel mit 4 Füssen wenn wir genau eine vertikale SChnittebene durch die Hälfte des Sessels legen, wissen wir das die Resultierende von je 2 Tischfüssen genau in dieser Ebene liegt. Somit können wir dieses System zweidimensional in dieser Ebene betrachten.
Die tiefe interessiert nicht. Die Drehmomente die wir da berechnen drehen aber um die Raumtiefe x sind also alles Mb x.
Wobei das Zeichenblatt die Koordinaten z,y erfasst und die Kräfte die man da aufs blatt papier zeichnet das Blattpapier drehen um eine Achse die ins Papier geht also die Raumtiefe die x Achse. Also Mb (x)
Stell dir nun die drei Raumachsen vor x,y,z vor.
Nimm nun die x Achse her und mache lauter vertiakle Schnittebenen drauf im Raum. Diese Schnittebenen haben y,z Koordinaten die legst du alle ineinander und tust so als ob die Raumtiefe y nicht existiert.
Du presst also alles zusammen auf y=0.
Alle Kräfte die in diesen Schnittebenen ersichtlich sind drehen um x sind also Mb(x).
das gleiche Machst du mit der y Achse presst sie zusammen.
Du hast dann Schnittebenen x,z die um y drehen als Mb(y)
und schließlich presst du noch die z Achse zusammen.
hast dann Schnittebenen x,y und die drehen um z.
Das ist die ganze Beschreibung im dreidimensioalen Raum
Also Schnittebene.
y,z dreht um x -> Mb (x)
x,z dreht um y -> Mb (y)
x,y dreht um z-> Mb (z)
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 14. Jan 2010 04:21 Titel: 3d Moment VeryApe Verfasst am: 14. Jan 2010 04:21 Titel: 3d Moment |
 |
|
Bitte gib hier Deine Frage ein. Welche Lösungsansätze sind Dir selbst dazu eingefallen? Was hast Du schon probiert? Bedenke, dass wir hier Hilfe zur Selbsthilfe leisten und keine Komplettlösungen liefern werden. Viel Erfolg!
| Beschreibung: |
|

Download |
| Dateiname: |
3d Moment.jpg |
| Dateigröße: |
72.72 KB |
| Heruntergeladen: |
10729 mal |
|
|
 |
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
 Physinetz Verfasst am: 14. Jan 2010 15:54 Titel: Physinetz Verfasst am: 14. Jan 2010 15:54 Titel: |
 |
|
also vielen Dank an beide, waren beide gute Tipps...
Hat mir sehr weitergeholfen, vielen Dank.
Also für die x und z Achse, also M(z)(B) und M(x)(B) schaff ich das jetzt mit VeryApe's Methode, nur um die y-Achse habe ich meine Schwierigkeiten:
Wenn ich also eine gedachte Ebene konstruiere, um die Y-Achse, wäre das ja die z-x-Ebene, wie auch in der Zeichnung von dir schön zu sehen ist VeryApe.
Wenn ich jetzt alle Kräfte auf diese Ebene gedanklich projeziere, dann sind die, die drehen für mich aber:
Z(A), X (A) , F und X (C) . Weil diese verlaufen ja dann alle in der Ebene, wenn man die Ebene mit keiner Dicke versieht, wie du beschrieben hast, also alles auf eine Ebene projiziert.
Aber Z(A) und X (A) sind ja laut Lösung nicht richtig,wenn ich es aber mit deiner Methode mache, dann wären die da auch dabei. Oder müssen die Kräfte jetzt nicht nur einen Hebelarm zu B haben sondern auch einen Hebelarm zur Achse (hier y-Achse). Und da die Kräfte direkt in der Achse angreifen, wäre das nicht möglich?
Also da haperts noch ein bisschen...
Danke nochmal für die Hilfe, speziell die Zeichnungen (macht ja auch Mühe)..
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 14. Jan 2010 23:31 Titel: VeryApe Verfasst am: 14. Jan 2010 23:31 Titel: |
 |
|
Okay das mit dem zusammenpressen hast du also kapiert.
Wenn du alles in eine Ebene presst und die Vektoren in dieser Ebene nur als dimensionlose Punkte erscheinen, sprich keine Beträge haben dann können sie auch in dieser Ebene nix bewirkt dimensionlos = 0 = Aktion.
Das siehst du beim Quader beispiel und hast es hoffentlich auch verstanden
gehen wir das ganze nochmal durch und schauen mal welche Kraftvektoren in den Ebenen überhaupt mit ihren Beträgen erscheinen und nicht als dimensionslose Punkte und somit keine Aktion ausführen.
Pressen wir das ganze in der Höhe zusammen also z=0
Wir erhalten eine x,y Ebene
Kräfte mit Beträge: XA, XB , XC
Kräfte als Punkt: F , ZB , ZA
Kräfte die um B drehen: XA, XC -> M(z)
Nun pressen wir das ganze in x zusammen wir erhalten
eine z,y Ebene
Kräfte mit Beträge: ZA, ZB, F
Kräfte als Punkt: XA,XB,XC
Kräfte die um B drehen -> ZA und F -> M(x)
Nun pressen wir wird die y Achse zusammen wir erhalten
eine z,x Ebene
Kräfte mit Beträge: alle ZA,ZB,F,XA,XB,XC
Kräfte als Punkt: ->0
Kräfte die um B drehen: XC und F
ZA ZB XA und XB liegen alle im Drehpunkt B sie haben ja keinen x oder z Versatz zu B und somit keinen Hebelarm sie liegen ja alle im Ursprung der z,x Koordinaten.
Um welche Länge sollen denn deiner Meinung nach XA und ZA in einer z,x Ebene drehen wenn die Abstände in y zusammengepresst wurden.
a wird ja dann null.. Du presst alles in Richtung y zusammen.
|
|
 |
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
 Physinetz Verfasst am: 15. Jan 2010 10:32 Titel: Physinetz Verfasst am: 15. Jan 2010 10:32 Titel: |
 |
|
ok ich glaube ich habe es kapiert...ich suche jetzt mal eine Übungsaufgabe und schaue ob ichs kann, falls nicht melde ich mich nochmal...
aber die "Technik" mit dem zusammenpressen ist echt nicht schlecht, weil man dann leicht auch die Hebelarme sieht...
nochmals danke veryape, klasse Hilfe!
|
|
 |
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
 Physinetz Verfasst am: 15. Jan 2010 11:46 Titel: Physinetz Verfasst am: 15. Jan 2010 11:46 Titel: |
 |
|
|
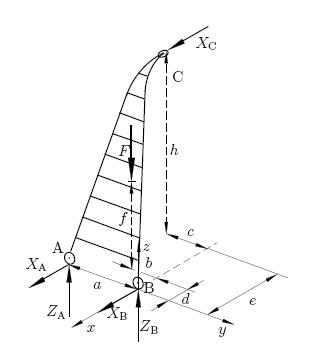
so...habe es jetzt mal an einer anderen Aufgabe versucht, nur da ist diese Methode ein wenig zu aufwendig...denke wohl das man am einfachsten doch über das Kreuzprodukt geht, oder?
|
|
 |
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
 Physinetz Verfasst am: 15. Jan 2010 12:06 Titel: Physinetz Verfasst am: 15. Jan 2010 12:06 Titel: |
 |
|
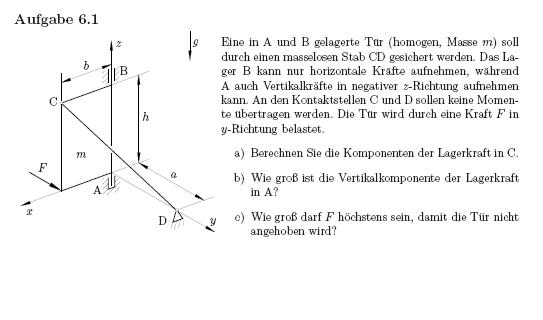
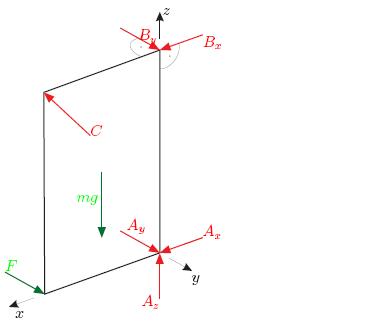
so da ich es trotzdem auf deine Methode versuchen will, hier mal das freigeschnittene Bild einer Türe, mit einzeichneten Kräften. die aufgabe, falls jemand sie braucht, lade ich auch mal mit hoch
Zu Beachten ist, dass die Kraft C schräg im Raum liegt, also Komponenten in x,y, und z Richtung hat.
Jetzt nach deiner Methode nur mal die Momente für x: Also }) : :
Da habe ich die Kräfte mit Beträgen:
F , m*g , C und B(y)
nun fallen m*g und F gleich weg, weil kein Hebelarm...
also für B(y) ist der Hebelarm h , also die Höhe der Türe nur mein Problem mit C:
Die Kraft C hat ja Komponenten in x,y und z Richtung, und genau da fängt dann das Problem an, dass ich nicht weiß welche Komponente ich nehmen muss für das Moment }) . .
C(x) ist es sicherlich nicht, wohl aber C(y) und C(z) könnten es sein...hier wäre dann wohl die Methode mit Kreuprodukt einfacher?
Bevor ich noch mit einer finalen Runde dieses Topic dann schließen will, hätte ich hier gerne nochmal Hilfe
Dankeschön!
| Beschreibung: |
|
| Dateigröße: |
26.52 KB |
| Angeschaut: |
37116 mal |
|
| Beschreibung: |
|
| Dateigröße: |
7.93 KB |
| Angeschaut: |
37116 mal |
|
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 15. Jan 2010 17:19 Titel: 2 Teil VeryApe Verfasst am: 15. Jan 2010 17:19 Titel: 2 Teil |
 |
|
...
| Beschreibung: |
|
| Dateigröße: |
28.08 KB |
| Angeschaut: |
25633 mal |
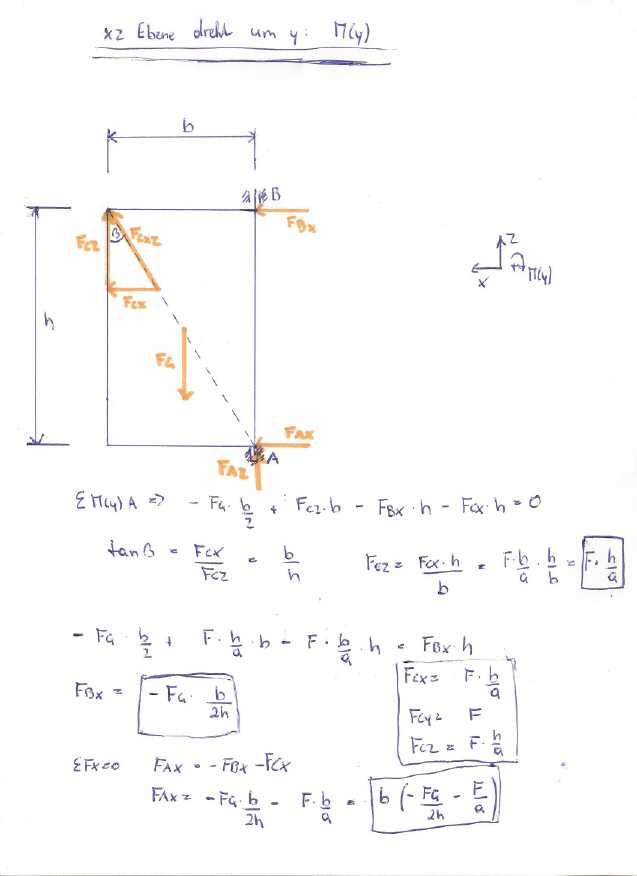
|
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 15. Jan 2010 17:22 Titel: 3 Teil VeryApe Verfasst am: 15. Jan 2010 17:22 Titel: 3 Teil |
 |
|
...
| Beschreibung: |
|
| Dateigröße: |
59.62 KB |
| Angeschaut: |
25587 mal |

|
|
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3247
|
 VeryApe Verfasst am: 15. Jan 2010 18:53 Titel: VeryApe Verfasst am: 15. Jan 2010 18:53 Titel: |
 |
|
sorry FAy und Fby sind natürlich nicht null.
Die Summe aller Fy sagt nur das sie zusammen gleich null sein müssen.
Das geht aber auch wenn sie einen wert haben und entgegengesetzt gleich groß sind.
Ich war zu voreilig und hätt auch die yz Ebene komprimiert zeichnen müssen.
Physinetz zeichnest du mal yz Ebene und errechnest FBy und FAy..
Die anderen sachen stimmen aber.
|
|
 |
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
 Physinetz Verfasst am: 17. Jan 2010 10:58 Titel: Physinetz Verfasst am: 17. Jan 2010 10:58 Titel: |
 |
|
ich versuche mich mal dran, sobald ich Zeit finde...und schreibe hier dann nochmal rein
gruß physi
|
|
 |
|