| Autor |
Nachricht |
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
 Physinetz Verfasst am: 13. Nov 2009 19:41 Titel: Resultierendes Moment : Aufgabe |
 |
|
Hallo,
ohne großes tara, hier die Aufgabe:
 http://s12.directupload.net/images/091113/toee2nqz.jpg
Also den resultierenden Vektor zu berechnen habe ich geschaft
Nur verstehe ich nicht ganz wie ich das Moment bezüglich
a) P berechne
b) Q berechne.
Ich weiß, dass das Moment berechnen lässt über das Kreuzprodukt von wirkender Kraft und Hebel.
Das resultierende Moment wäre:
Jetzt die Frage:
Was sind denn hier überhaupt meine Hebel. Wenn ich den Tetraeder in ein Koordinatensystem lege, mit P im Ursprung, dann wäre ja mein Hebel im Punkt P : der Ortsvektor zu P , also der Nullvektor, folglich hätte ich das Moment 0 ?
Im Punkt Q wäre es der Vektor PQ?
Und was ist dann die Kraft? Weil in der Aufgabe heißt es ja nur dass ich ein Tetraeder habe, und dann eben einen resultierenden Vektor, aber von einer Kraft ist doch nicht mal die Rede?
Viell. kann mir da mal jemand ziemlich auf die Sprünge helfen....
Danke !!!
PS: Bitte ausführlich, danke für Eure Mühe |
|
 |
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
| Physinetz Verfasst am: 14. Nov 2009 08:52 Titel: |
|
|
Mir wurde gesagt, dass man auch beachten müsse ob die Pfeile auf den Punkt zeigen oder nicht, ist da was dran?
Weil 3 Pfeile zeigen ja in die "Höhe", aber diese 3 Vektoren kann man ja so verschieben , dass auch Sie im Punkt P angreifen, durch einfaches Vektorverschieben: oder ist das bei Kräften nicht erlaubt?.
Falls nicht erlaubt: Welche Vektoren greifen dann am Punkt P an? Nur derjenige, bei dem die Pfeilspitze auf ihn zeigt, oder auch diejenigen, die ihr Vektorende (also Pfeilende) am Punkt P haben und von diesem dann ausgehen (also die Vektoren die ihren Ursprung in P haben (sind ja 2 laut Zeichnung))
Danke für eure Hilfe (bitte auch den oberen Teil beachten) |
|
|
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
| Physinetz Verfasst am: 14. Nov 2009 10:17 Titel: |
|
|
Ok jetzt hab ich wieder was rausgefunden, super :-D
Vektorverschieben bei Kräften ist nicht, nur entlang ihrer Wirkungslinie, somit greifen im Punkt P lediglich 2 Vektoren an (der der auf P zeigt, und der der von P in die Höhe zeigt).
Im Punkt Q greifen dann 3 Kräfte an, richtig?
Nur wie jetzt weiter? |
|
|
GvC
Anmeldungsdatum: 07.05.2009
Beiträge: 14861
|
| GvC Verfasst am: 14. Nov 2009 13:11 Titel: |
|
|
| Physinetz hat Folgendes geschrieben: | | Vektorverschieben bei Kräften ist nicht, nur entlang ihrer Wirkungslinie |
Das stimmt, sofern Du die Momente bestimmen willst, denn M = F x a (Kreuzprodukt aus Kraft-und Abstandsvektor). Für die Bestimmung der Kräftesumme kannst Du, nein, musst Du sogar die Kräfte parallel verschieben. Wie sonst kannst Du sie sonst addieren? Übrigens: Die Momentenvektoren, also das jeweilge Vektorprodukt aus Kraft und Abstand, kannst bzw. musst Du ebenfalls parallel verschieben, um das Gesamtmoment bzgl. eines Bezugspunktes zu erhalten. |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 14. Nov 2009 16:42 Titel: |
|
|
| GvC hat Folgendes geschrieben: | | M = F x a |
 |
|
|
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
| Physinetz Verfasst am: 14. Nov 2009 20:05 Titel: |
|
|
Ok und wie gehe ich nun in der Aufgabe oben vor?
Wie bestimme ich das Moment bezüglich
a) dem Punkt P
b) dem Punkt Q
oben habe ich ja schon geschrieben
bei P: zwei Vektoren
bei Q: dann drei Vektoren die wirken...? Richtig?
Und P ist ja Nullvektor wenn ich da meinen Ursprung. hinsetze? Dann wäre das Moment bei P ja Null? Wenn ich aber den Ursprung an Q setze, dann habe ich ja plötzlich bei Q das Moment 0 ?
Bitte Um Aufklärung!! |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 15. Nov 2009 08:38 Titel: |
|
|
Bezüglich P hast du 3 Vektoren, die nicht durch P gehen und somit zum Moment beitragen.
Generell:
brute force:
Schreibe die Kräfte und deren Angriffspunkte in x, y, z Komponenten an und bilde das äussere Produkt beider Grössen. Ist vielleicht etwas Rechnerei, aber nicht kompliziert.
eleganter:
Du suchst einen Punkt r0 , bezüglich dessen sich das Moment einfach hinschreiben lässt und verwendest dann
 \times r_0 + \sum_i F_i \times r_i' = F_{ges} \times r_0 + \sum_i F_i \times r_i')
für
jedenfalls kannst du so von P auf Q kommen oder von Q auf P ... , ohne viel Vektorgymnastik. 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
| Physinetz Verfasst am: 15. Nov 2009 12:45 Titel: |
|
|
| Zitat: | | Bezüglich P hast du 3 Vektoren, die nicht durch P gehen und somit zum Moment beitragen. |
Wieso tragen die Vektoren, die durch P gehen, nicht zum Moment bei?
Muss ich P in diesem Fall als den "Drehpunkt" sehen, also als ob ein Hebel am Punkt P befestigt wäre und der sich nun drehen kann? Und wenn eine Kraft am Drehpunkt angreift passiert praktisch nichts?
Doch wie finde ich dann "r" also meine Hebel immer raus? Hier ist ja gar kein Hebel gegeben sondern immer nur Vektoren (Kräfte) |
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 15. Nov 2009 13:06 Titel: |
|
|
| schnudl hat Folgendes geschrieben: | | Bezüglich P hast du 3 Vektoren, die nicht durch P gehen und somit zum Moment beitragen. |
| Physinetz hat Folgendes geschrieben: | | Muss ich P in diesem Fall als den "Drehpunkt" sehen, also als ob ein Hebel am Punkt P befestigt wäre und der sich nun drehen kann? Und wenn eine Kraft am Drehpunkt angreift passiert praktisch nichts? |
Richtig. Ein Moment bestimmst du immer bezüglich eines Bezugspunktes. Ein Moment ist Kraft mal Hebelarm. Wenn der Kraftvektor durch diesen Bezugspunkt zeigt, ist der Hebelarm null, diese Kraft trägt nichts zum Gesamtmoment bei.
| Physinetz hat Folgendes geschrieben: | | Doch wie finde ich dann "r" also meine Hebel immer raus? Hier ist ja gar kein Hebel gegeben sondern immer nur Vektoren (Kräfte) |
Die Kräfte sind bei der Momentenberechnung an ihre Wirkungslinien gebunden, es spielt eine Rolle, wo (in der Ebene senkrecht zu ihrer Richtung) sie platziert sind. Diese 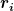 sind Ortsvektoren der Kraftvektoren. |
|
|
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
| Physinetz Verfasst am: 15. Nov 2009 14:21 Titel: |
|
|
das hilft mir sehr weiter hier:
| Zitat: | | Wenn der Kraftvektor durch diesen Bezugspunkt zeigt, ist der Hebelarm null, |
Das heißt der Hebelarm ist :
Ortsvektor an dem die Kraft angreift Minus Ortsvektor des Bezugspunkts
Dann bekomme ich den "Hebel"vektor, also Vektor "r".
Beispiel für das Moment am Punkt P:
Ein wirkender Vektor wäre ja z.B. gerade der Vektor , wo in der Skizze das a steht, also der Vektor a (zeigt aus der Skizze heraus). Nennen wir ihn a_1
Jetzt müsste ich als Hebelarm PQ nehme, also den Vektor
mit dem Betrag a
und als Kraft nur den senkrechten Anteil des Vektors a_1 , dieser Anteil lässt sich über Phytagoras berechnen.
Und dann muss ich das Kreuzprodukt der beiden Vektoren nehmen, richtig?
Hoffe es zumindest
Vielen Dank, hilft mir aufjedenfall schonmal sehr weiter! |
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 15. Nov 2009 15:42 Titel: |
|
|
| Physinetz hat Folgendes geschrieben: | Das heißt der Hebelarm ist :
Ortsvektor an dem die Kraft angreift Minus Ortsvektor des Bezugspunkts
Dann bekomme ich den "Hebel"vektor, also Vektor "r". |
Wenn du den Bezugspunkt gleich als Koordinatenursprung wählst, ist's einfacher. 
Dann ist die Hebelarmlänge genau dann der Betrag des Ortsvektors, wenn Ortsvektor und Kraftwirkungslinie senkrecht aufeinander stehen.
| Zitat: | ="Physinetz"]Jetzt müsste ich als Hebelarm PQ nehme, also den Vektor
mit dem Betrag a
und als Kraft nur den senkrechten Anteil des Vektors a_1 , dieser Anteil lässt sich über Phytagoras berechnen.
Und dann muss ich das Kreuzprodukt der beiden Vektoren nehmen, richtig? |
Der Witz ist, dass das Kreuzprodukt dir diese ganze Pythagoras-Sache schon abnimmt. Das merkst du z.B., wenn du das Kreuzprodukt paralleler Vektoren rechnest, das gibt immer null: Der Hebelarm verschwindet. Bei senkrecht aufeinander stehenden (z.B. in x- und y-Richtung) Vektoren kriegst du beim Kreuzprodukt einen Vektor, der senkrecht auf beide steht (z.B. in z-Richtung) und dessen Betrag das Produkt aus den Beträgen der beiden Vektoren ist.
 wobei  der Vektor vom Bezugspunkt zum Kraftangriffspunkt ist.
Wichtig ist: Ein Moment ist in der räumlichen Vektorgeometrie auch ein Vektor, nicht ein Skalar! |
|
|
franz
Anmeldungsdatum: 04.04.2009
Beiträge: 11583
|
| franz Verfasst am: 15. Nov 2009 16:02 Titel: |
|
|
|
Erinnerung: M = r X F. |
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 15. Nov 2009 16:11 Titel: |
|
|
| franz hat Folgendes geschrieben: | | Erinnerung: M = r X F. |
Richtig. Gemäss Konvention gilt die rechte-Hand-Regel. Der Daumen ist die Vektorrichtung, die Finger der rechten Hand drehen in Momentenrichtung um den Daumen. Mit F x r würde der M Vektor in Gegenrichtung gerichtet sein. Danke für den Hinweis. |
|
|
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
| Physinetz Verfasst am: 15. Nov 2009 16:57 Titel: |
|
|
Erstmal Danke an Gajeryis, echt super Hilfe , und an den Rest natürlich auch.
Also mir leuchtet fast alles ein. Bis auf etwas ...:
Also wenn ich von zwei Vektoren das Kreuzprodukt nehme, bekomme ich immer (außer bei Spezialfällen) den senkrechten Vektor heraus, der senkrecht zu beiden Vektoren ist, stimmt doch oder?
Nur verstehe ich nicht ganz, wieso ich trotzdem bei der Kraft nicht über Pythagoras den senkrechten Anteil ausrechnen muss.
Die Richtung ist ja immer diegleiche (egal ob senkrechter Anteil oder ganze Kraft), aber wenn ich nur den senkrechten Anteil nehme vom Vektor dann wird der Betrag des Moments doch kleiner?
Also mir ist eben noch nicht klar wieso man einfach das Kreuzprodukt von Kraft und Hebelarm macht und nicht senkrechtem Kraftanteil und Hebelarm, um es auf den Punkt zu bringen.
Irgendwie hilft mir da auch nicht weiter:
| Zitat: | | Das merkst du z.B., wenn du das Kreuzprodukt paralleler Vektoren rechnest, das gibt immer null: Der Hebelarm verschwindet. Bei senkrecht aufeinander stehenden (z.B. in x- und y-Richtung) Vektoren kriegst du beim Kreuzprodukt einen Vektor, der senkrecht auf beide steht (z.B. in z-Richtung) und dessen Betrag das Produkt aus den Beträgen der beiden Vektoren ist. |
Vielleicht hat da jemand noch ein paar Beispiele etc...?
Ich bedanke mich ! |
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 15. Nov 2009 17:39 Titel: |
|
|
Applet zum Vektorprodukt:
http://moltke.homeip.net/daten/auto/kap08/applets/cd209.htm
Spiele dort mal mit den Winkeln. Dann wirst du sehen, dass der Betrag des AxB-Vektors je kleiner wird, desto kleiner der Winkel zwischen den Vektoren A und B ist.
Mathematisch:
Ortsvektor r sei
Kraftvektor F sei
Moment um den Ursprung M sei
Damit sehen wir:
Sprich, die "Pythagoras"-Rechnung wurde schon im Kreuzprodukt übernommen: |r| * cos(alpha) ist schon die Länge des Hebels senkrecht auf die Wirkungslinie. |
|
|
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
| Physinetz Verfasst am: 15. Nov 2009 20:55 Titel: |
|
|
|
sehr schön, habs glaub gecheckt, nochmals danke für die tolle hilfe |
|
|
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
| Physinetz Verfasst am: 17. Nov 2009 20:37 Titel: |
|
|
also ich habs geblickt, aber anscheinend doch nicht, weil ich hier die Lösung für b) habe:
Man soll das Moment bezüglich Q Berechnen.
Lösung laut Uni:
http://s12.directupload.net/images/091117/qufcjkyq.jpg
Mein Problem,
ich dachte ich muss bei der Berechnung des Moments Q , dass ich die Vektoren des Hebels von Q mit der Kraft im Kreuzprodukt nehmen muss.
D.h. hier in meiner schöneren Skizze:
http://s5.directupload.net/images/091117/gsat93n7.jpg
Vektor    
Dann bekomme ich das Gesamtmoment, wieso addieren die hier noch das Moment von P ? Bei Q habe ich ja nur 3 Vektoren, deren Hebel ungleich 0 ist, dass ist wie gesagt:  .
Hoffe da kann mir jemand helfen...Danke!!
PS: Also bei Moment bezüglich P haben wir ja auch nur 3 Vektoren beachtet, deren Hebel (also Ortsvektor zur Kraft von P ) eben ungleich 0 ist. |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 17. Nov 2009 20:44 Titel: |
|
|
Das entspricht genau dem, was ich oben schon geschrieben habe:
| schnudl hat Folgendes geschrieben: |
...
eleganter:
Du suchst einen Punkt r0 , bezüglich dessen sich das Moment einfach hinschreiben lässt und verwendest dann
für
jedenfalls kannst du so von P auf Q kommen oder von Q auf P ... , ohne viel Vektorgymnastik. |
Wenn man Mp und die Resultierende A weiss, kommt man damit zu Mq...
Du brauchst also, um Mq zu bekommen nicht alles nochmals durchzuexerzieren, sondern bloss den fehlenden Term zu Mp dazuzuaddieren. Es ist so ähnlich wie der Steiner'sche Satz (etwas weit hergeholt...)
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 17. Nov 2009 23:00 Titel: |
|
|
|
Das numerische Ergebnis sollte für beide Methoden dasselbe sein, wenn du nirgends einen Rechenfehler gemacht hast (passiert leider schnell). |
|
|
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
| Physinetz Verfasst am: 17. Nov 2009 23:11 Titel: |
|
|
Ok nun mal unabhängig von deinem Satz...
Nochmal:
| Zitat: | Vektor
Dann bekomme ich das Gesamtmoment, wieso addieren die hier noch das Moment von P ? Bei Q habe ich ja nur 3 Vektoren, deren Hebel ungleich 0 ist, dass ist wie gesagt: . |
Wenn ich mir das nüchtern betrachte ohne deine Herleitung, ich habe doch nur dann 3 Hebel? Die anderen 3 Kräfte die direkt im Punkt P angreifen brauch ich doch gar nicht mehr zu beachten.... Dann kann ich doch auch einfach wie oben beschrieben die Vektorprodukte nehmen von :
Vektor ...Das müstte doch eigentlich richtig sein (ohne dein Formle betrachtet zu haben).
Nun zu deiner "Formel":
Da komme ich nicht so ganz mit, was ist denn das  und dass  ?
Das Moment ist ja die Summe der Kreuzprodukte  also jeweiliger Hebel (Ortsvektor vom Bezugspunkt zum Punkt wo die Kraft angreift) gekreuzt mit der Kraft die an dem Hebel zerrt. Das ist ja der erste Term....richtig?
Nur was du dann machst ist mir nicht so klar, dass du plötzlich ein r_0 hast und dann die gesamten Kräfte aufsumierst und diese dann mit dem Hebel r_0 kreuzt (das darf man doch gar nicht weil man jedes Moment einzeln berechnen muss). Und hinten addierst du noch irgendwas mit r_i' ? Was ist dann r_i'
Wäre gut wenn du mir den Fehler meiner Lösung erklären könntest (siehe ganz oben) und dann den Teil ab: Nun zu deiner "Formel" .
Also nicht beides vereinen, dankeschön |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 18. Nov 2009 09:59 Titel: |
|
|
Jeder Aufpunkt im Bezugssystem Q ist gegeben durch den Aufpunkt im Bezugssytem P plus dem fixen Abstand zwischen P und Q:
Das setzt du in die Definition des Moments bez. Punkt Q ein...
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
Physinetz
Anmeldungsdatum: 20.09.2006
Beiträge: 317
|
| Physinetz Verfasst am: 18. Nov 2009 19:25 Titel: |
|
|
Ok wenn auf meine Art und Weise das gleiche rauskommt dann bin ich schonmal beruhigt,
nur deine Formel dämmert mir einfach nicht, ich bin da wohl ein bisschen beschränkt 
Soll das mit dem Aufpunkt bedeuten:
Den Punkt P erhalte ich über: Ortsvektor Q + Vektor PQ ?
Aber wie dass dann mit der Formel zusammenhängt leuchtet mir nicht ein |
|
|
Gajeryis
Anmeldungsdatum: 08.10.2009
Beiträge: 194
Wohnort: CH - Bern
|
| Gajeryis Verfasst am: 18. Nov 2009 20:12 Titel: |
|
|
Die resultierende Kraft einer Kräftegruppe ist für alle beliebigen Bezugspunkte gleich.
Das resultierende Moment ist aber vom Ort des Bezugspunktes abhängig. Wenn du das Moment für einen bestimmten Punkt kennst (z.B. weil es für diesen Punkt sehr einfach auszurechnen ist), kannst du es für jeden anderen Punkt ebenfalls ausrechnen.
Wenn du also das Moment in Punkt A berechnet hast:
kannst du das Moment auch für einen anderen Punkt B berechnen.
Denn, wie du richtig vermutet hast, gilt 
Also ist auch 
Da für das Kreuzprodukt das Distributivgesetz auch gilt: (  = \vec{a} \times \vec{b} + \vec{a} \times \vec{c}) ) ergibt sich dann
 |
|
|
|
Registrieren
Login
FAQ
Suchen
