| Autor |
Nachricht |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 07. Mai 2007 20:44 Titel: Adiabatische Expansion Gargy Verfasst am: 07. Mai 2007 20:44 Titel: Adiabatische Expansion |
 |
|
Hallo, ich brauche mal hilfe bei einer Aufgabe:
Der Einzylindermotor eines Motorads hat ein Kompressionsverhältnis von 6:1. Der Kolben verursacht eine maximale Volumenänderung im Zylinder von 200cm³.
Wie groß ist die Leistung durch die Expansion des Gases, wenn der Motor eine Drehzahl 3000 U/min hat?
Es wird adiabatische Expansion eines idealen Gases mit  vorrausgesetzt. vorrausgesetzt.
Ich habe mir gedacht, die Leistung berechnet sich ja folgendermaßen:
 n = Drehzahl n = Drehzahl
Also müsste ich nur die Ausdehnungsarbeit des Gases berechnen. Da komme ich aber nicht weiter. Zum einen fehlt die Angabe eines Adiabatenexponenten und außerdem scheitere ich schon am "Kompressionsverhältnis". Was soll das denn sein? Verhalten sich die Drücke wie 6:1 oder die Volumina? 
 |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 08. Mai 2007 10:59 Titel: Gargy Verfasst am: 08. Mai 2007 10:59 Titel: |
 |
|
Aha, gut, dann kann ich also die Volumina ausrechnen.
Adiabatenexponent über die Freiheitsgrade? Nein, das muss ich erst nachlesen. Ich schau das am besten mal nach und komm dann nochmal her.
Wenn ich den Exponenten habe, könnte ich mit den Volumina und dem gegeben Druck dann die Temperaturen bestimmten (mit der Zustandsgleichung) und damit dann die Arebit ausrechnen... Ist das soweit richtig?
Vielen Dank schon mal.  |
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 08. Mai 2007 15:58 Titel: Gargy Verfasst am: 08. Mai 2007 15:58 Titel: |
 |
|

Aber wieviele Freiheitsgrade hat denn ein ideales Gas? 3? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 08. Mai 2007 16:45 Titel: dermarkus Verfasst am: 08. Mai 2007 16:45 Titel: |
 |
|
Achtung, ich glaube, da ist dir beim Abschreiben der Formel ein Tippfehler unterlaufen.
Wieviel Freiheitsgrade die Teilchen eines idealen Gases haben, kommt auf die Teilchen an. Luftmoleküle wie  und und  sind zweiatomig und haben fünf Freiheitsgrade, siehe zum Beispiel in sind zweiatomig und haben fünf Freiheitsgrade, siehe zum Beispiel in
http://www.tu-chemnitz.de/physik/PHFK/LEHRE/SCRIPT/thermo.pdf
auf Seite 3 (= Seite 7 von 47) |
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 08. Mai 2007 16:55 Titel: Gargy Verfasst am: 08. Mai 2007 16:55 Titel: |
 |
|

aber ich weiß doch nicht, welches gas ich habe! ich weiß nur, dass es ein ideales gas sein soll... |
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 08. Mai 2007 16:59 Titel: Gargy Verfasst am: 08. Mai 2007 16:59 Titel: |
 |
|
|
meinst du, dass ich die aufgabe so lösen soll? gibt's nicht vielleicht noch einen andern weg? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 08. Mai 2007 17:00 Titel: dermarkus Verfasst am: 08. Mai 2007 17:00 Titel: |
 |
|
Einverstanden, so stimmt die Formel 
In so einem Zylinder eines Motorrad-Motors wird sicher ein Luft-Treibstoff-Gemisch drinsein, das sowohl vor als auch nach der Verbrennung ziemlich viel (wohl rund 70% oder knapp 70%) Stickstoffmoleküle enthält.
Ich würde also vorschlagen, das mal mit dem Koeffizienten für Luft zu berechnen. |
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 08. Mai 2007 17:06 Titel: Gargy Verfasst am: 08. Mai 2007 17:06 Titel: |
 |
|
ach so, stimmt ja, also ist 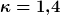 |
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 08. Mai 2007 19:04 Titel: Gargy Verfasst am: 08. Mai 2007 19:04 Titel: |
 |
|
Sooo, jetzt kann ich die Volumina und die Drücke ausrechnen.
E=Expansion, K=Kompression




Aber wie mache ich weiter?
Ich hatte mir gedacht, die Arbeit folgendermaßen auszurechnen:

Allerdings kriege ich die Temperaturen nicht raus.
dT kann ich noch ersetzen mit dem Differential der Zustandsgleichung:
}{nR})
Das nR verschwindet, wenn ich  ersetze mit ersetze mit 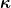 . .
)
Hehe, ich glaube, ich stelle mich jetzt etwas dümmlich an, aber... wie integriere ich das? Ich meine, was setze ich für p und für V ein?
 |
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 08. Mai 2007 21:13 Titel: Gargy Verfasst am: 08. Mai 2007 21:13 Titel: |
 |
|
 |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 08. Mai 2007 21:50 Titel: dermarkus Verfasst am: 08. Mai 2007 21:50 Titel: |
 |
|
| Gargy hat Folgendes geschrieben: |
)
|
Dein Ansatz ist richtig, allerdings finde ich ihn etwas komplizierter als nötig.
Integrieren könntest du nun wie folgt:
 \dd V + \int_{p_1}^{p_2} V(p) \dd p \right))
Die Integralgrenzen sind die Volumina und Drücke am Anfang und Ende des Ausdehnungsvorganges, und die Funktionen p(V) und V(p) bekommt man aus

Die Konstante c bekommst du zum Beispiel aus den Werten von p und V am Anfang des Vorganges.
-------------------------------------------------
Einfacher kommst du allerdings zum Ergebnis, wenn du direkt die Fläche unter der Kurve im p-V-Diagramm ausrechnest:
 \dd V=...)  |
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 09. Mai 2007 08:33 Titel: Gargy Verfasst am: 09. Mai 2007 08:33 Titel: |
 |
|
 )
Richtig?  |
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 09. Mai 2007 08:51 Titel: Gargy Verfasst am: 09. Mai 2007 08:51 Titel: |
 |
|
Ich habe das jetzt mal eingesetzt:

^{1,4} \cdot ln(\frac{240^{1,4}}{40^{1,4}}))

Sooo, damit habe ich die Arbeit. Dann würde ich das jetzt einfach mit der Drehzahl multiplizieren und hätte die Leistung. Aber... hm, kann man das einfach so machen? Gefragt ist ja nur nach der Leistung bei Expansion. Die Drehzahl gibt aber die Umdrehungen für einen vollen Kreis... also halbe Drehzahl? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. Mai 2007 13:41 Titel: dermarkus Verfasst am: 09. Mai 2007 13:41 Titel: |
 |
|
| Gargy hat Folgendes geschrieben: |  ) |
Ich meine, da hast du dich beim Integrieren vertan. Ich bekomme beim Integrieren eine andere Stammfunktion als  . .
| Gargy hat Folgendes geschrieben: |
Gefragt ist ja nur nach der Leistung bei Expansion. |
Nicht ganz. In der Aufgabenstellung steht "Leistung durch die Expansion". Also die Motorleistung, die man dadurch bekommt, dass sich das Gas im Kolben einmal pro Umdrehung ausdehnt. |
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 09. Mai 2007 14:02 Titel: Gargy Verfasst am: 09. Mai 2007 14:02 Titel: |
 |
|

+ C)
So? Und wie rechnet man das aus? Normal setzt man doch W(V=0)... Nicht? Aber kann man das überhaupt lösen?
Hm, oder was meinst du sonst? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. Mai 2007 14:08 Titel: dermarkus Verfasst am: 09. Mai 2007 14:08 Titel: |
 |
|
Achtung, du rechnest das so, als ob die Integrationsvariable  wäre und nicht wäre und nicht 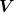 . .
Für die Integration von Funktionen  = x^a) brauchst du gar keinen brauchst du gar keinen 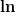 , wenn das , wenn das  nicht ausgerechnet gerade gleich -1 ist. nicht ausgerechnet gerade gleich -1 ist. |
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 09. Mai 2007 14:18 Titel: Gargy Verfasst am: 09. Mai 2007 14:18 Titel: |
 |
|
Ach so !!!
Also

So richtig? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. Mai 2007 14:21 Titel: dermarkus Verfasst am: 09. Mai 2007 14:21 Titel: |
 |
|
Ja, du meinst das Richtige  Jetzt stimmt deine Stammfunktion Jetzt stimmt deine Stammfunktion  |
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 09. Mai 2007 14:34 Titel: Gargy Verfasst am: 09. Mai 2007 14:34 Titel: |
 |
|
Gut, dann also
)
)
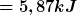
Und für die Leistung

Stimmt das? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. Mai 2007 14:49 Titel: dermarkus Verfasst am: 09. Mai 2007 14:49 Titel: |
 |
|
| Gargy hat Folgendes geschrieben: |
)
|
Hoppla, da scheinen mir gleich einige Flüchtigkeitsfehler auf einmal drin zu sein! Schreib das ganze am besten noch mal richtig sorgfältig und vollständig auf, also
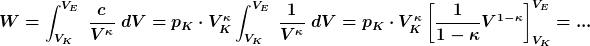 |
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 09. Mai 2007 14:58 Titel: Gargy Verfasst am: 09. Mai 2007 14:58 Titel: |
 |
|
 Das habe ich doch auch geschrieben? Wenn da ein Fehler drin ist, weiß ich nicht, an welcher Stelle... Meinst du, das Integral ist falsch oder die eingesetzten Werte? Das habe ich doch auch geschrieben? Wenn da ein Fehler drin ist, weiß ich nicht, an welcher Stelle... Meinst du, das Integral ist falsch oder die eingesetzten Werte?
edit// Ach so, die Exponente. Ja, das ist in der Formel falsch und müsste heißen  . Aber ansonsten...? . Aber ansonsten...? |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 09. Mai 2007 15:13 Titel: dermarkus Verfasst am: 09. Mai 2007 15:13 Titel: |
 |
|
Einverstanden, die Exponenten waren falsch gewesen. Aber du hast recht, das war nur ein Tippfehler, danach stimmts wieder, und ich komme bis auf Rundungsfehler auf dieselben Ergebnisse wie du 
Zuletzt bearbeitet von dermarkus am 09. Mai 2007 15:15, insgesamt einmal bearbeitet |
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 09. Mai 2007 15:15 Titel: Gargy Verfasst am: 09. Mai 2007 15:15 Titel: |
 |
|
 |
|
 |
Gargy

Anmeldungsdatum: 24.11.2006
Beiträge: 1046
|
 Gargy Verfasst am: 14. Mai 2007 20:24 Titel: Gargy Verfasst am: 14. Mai 2007 20:24 Titel: |
 |
|
hm, wir haben das 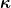 im im  vergessen... vergessen...
is ja unglaublich, scheinen noch ein paar kommilitonen die seite gefunden zu haben -  der fehler kam wohl öfter vor. der fehler kam wohl öfter vor.
 Selber überlegen macht schlau. Selber überlegen macht schlau. |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 15. Mai 2007 01:27 Titel: dermarkus Verfasst am: 15. Mai 2007 01:27 Titel: |
 |
|
Stimmt, beim Einsetzen der Werte hatten wir übersehen, dass beim ersten Vorkommen von  noch der Exponent noch der Exponent 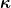 mit dranberechnet werden muss. mit dranberechnet werden muss.
Wenn einige deiner Kommilitonen denselben Fehler eingebaut hatten, spricht das in der Tat wohl für den Bekanntheitsgrad und den Google-Pagerank des Physikerboards  |
|
 |
|




















 der fehler kam wohl öfter vor.
der fehler kam wohl öfter vor.
 Selber überlegen macht schlau.
Selber überlegen macht schlau.