| Autor |
Nachricht |
pfnuesel
Anmeldungsdatum: 04.11.2004
Beiträge: 248
Wohnort: Zürich
|
 pfnuesel Verfasst am: 24. Apr 2007 12:18 Titel: Dirac-Notation pfnuesel Verfasst am: 24. Apr 2007 12:18 Titel: Dirac-Notation |
 |
|
Hallo
Habe Schwierigkeiten mit der Dirac-Notation (Bra- und Ket-Vektoren). Irgendwie blicke ich noch nicht ganz durch.
In meinem Script steht:
| Zitat: | Die Zustände  und und  sind noch nicht normiert: Sei sind noch nicht normiert: Sei  normiert, dann ist normiert, dann ist
 und und

und wir erhalten normierte Eigenvektoren, wenn wir definieren
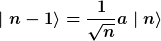 , ,
 . . |
wobei  , bzw. , bzw. 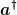 den Absteige-, bzw. Aufsteigeoperator bezeichnet und den Absteige-, bzw. Aufsteigeoperator bezeichnet und 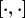 den Kommutator. den Kommutator.
Der erste Teil ist mir soweit noch klar, er folgt aus vorhergehenden Überlegungen, die ich hier nicht alle aufschreiben möchte. Aber was die Normierung zu bedeuten hat, wie sie zu verstehen ist und wie man auf diese Werte kommt, verstehe ich leider nicht. Das muss ja eine ganz einfache Rechnung sein, bloss habe ich so meine Mühe mit der Dirac-Notation, dass ich leider nicht drauf komme.
Kann mir jemand helfen? Vielen Dank! |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5786
Wohnort: Heidelberg
|
 as_string Verfasst am: 24. Apr 2007 12:49 Titel: as_string Verfasst am: 24. Apr 2007 12:49 Titel: |
 |
|
Hallo!
Ich habe jetzt noch nicht ganz verstanden, an welcher Stelle Du hängst.
Was Normierung eines Zustands bedeutet, weißt Du doch sicher. Für einen quantenmechanischen Zustand muss halt immer das hier gelten:

Die Zustände, die er zuerst erwähnt, erfüllen diese Bedingung nicht. Das zeigt er, indem er den Betrag der beiden Vektoren ausrechnet. Das rechnet er aus, indem er den jeweiligen Vektor mit seinem konjugierten multipliziert, so wie man halt Beträge solcher Vektoren ausrechnet.
Auf normale reelle Vektoren übertragen: Er rechnet das Skalarprodukt des Vektors mit sich selbst aus. Das ist gerade das Betragsquadrat. Nur dass man bei Vektoren mit komplexen Komponenten halt den konjugierten Vektor benutzen muss.
Gruß
Marco |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 24. Apr 2007 13:23 Titel: Re: Dirac-Notation dermarkus Verfasst am: 24. Apr 2007 13:23 Titel: Re: Dirac-Notation |
 |
|
Hallo,
vielleicht hilft es dir da zusätzlich, mal zu sehen, wie das, was man in der Dirac-Notation so schön kurz und knapp schreiben kann, zum Beispiel in der Ortsdarstellung aussehen würde:
Der Ket-Vektor  ist in Ortsdarstellung der Zustandsvektor ist in Ortsdarstellung der Zustandsvektor ) . .
Der zugehörige Bra-Vektor  ist in Ortsdarstellung der dazu konjugiert komplexe Vektor ist in Ortsdarstellung der dazu konjugiert komplexe Vektor ) . .
Das  ist in Ortsdarstellung das Integral ist in Ortsdarstellung das Integral  \Psi_n(\vec r) \, \dd \vec r) über den gesamten Raum. über den gesamten Raum.
Das ist also so wie das Skalarprodukt eines Vektors mit sich selbst, um das Betragsquadrat des Vektors auszurechnen, nur dass hier der Zustandsvektor in Ortsdarstellung nicht endlich viele Komponenten hat, deren Quadrate addiert werden, wie du es zum Beispiel vom Skalarprodukt bei dreidimensionalen Vektoren kennst, sondern unendlich viele Komponenten (nämlich eine Vektor-Komponente für jeden Wert von 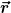 ), deren Produkte mit ihrem jeweils konjugiert komplexen Wert gebildet werden, die dann in einem Integral zusammengezählt werden. ), deren Produkte mit ihrem jeweils konjugiert komplexen Wert gebildet werden, die dann in einem Integral zusammengezählt werden.
Wirkt nun ein Operator auf so einen Zustandsvektor, dann können sich dabei natürlich sowohl die Richtung als auch die Länge des Ergebnisvektors von denen des ursprünglichen Zustandsvektors unterscheiden. Und damit auch der Ergebnisvektor wieder ein braver normierter (also mit Länge 1) Zustandsvektor ist, muss man den Ergebnisvektor, den man nach Anwenden des Operators erhält, noch mit einem passenden Normierungsfaktor multiplizieren 
------------------------
Magst du mal in Dirac-Notation ausprobieren, ob das ganze aufgeht, indem du zum Beispiel mal vom Zustand 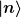 ausgehst, dann den Absteigeoperator mit passender Normierung laut der angegebenen Gleichungen darauf anwendest, und dann auf den Zustand, der da herauskommt, den Aufsteigeoperator mit passender Normierung anwendest? Kommst du damit dann wieder auf den richtig normierten ursprünglichen Zustand? ausgehst, dann den Absteigeoperator mit passender Normierung laut der angegebenen Gleichungen darauf anwendest, und dann auf den Zustand, der da herauskommt, den Aufsteigeoperator mit passender Normierung anwendest? Kommst du damit dann wieder auf den richtig normierten ursprünglichen Zustand? |
|
 |
pfnuesel
Anmeldungsdatum: 04.11.2004
Beiträge: 248
Wohnort: Zürich
|
 pfnuesel Verfasst am: 24. Apr 2007 21:18 Titel: pfnuesel Verfasst am: 24. Apr 2007 21:18 Titel: |
 |
|
Vielen Dank euch beiden für die Antworten.
Leider bin ich immer noch nicht ganz dahinter gestiegen.
Was bedeutet denn  ? Das ist doch der Erwartungswert von ? Das ist doch der Erwartungswert von  ? Suchen wir nicht den Erwartungswert von ? Suchen wir nicht den Erwartungswert von  , bzw. , bzw. 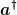 ? Wir wollen ja die Zustände ? Wir wollen ja die Zustände  , bzw. , bzw.  normieren. normieren.
Wenn ich den Erwartungswert der neu normierten Operatoren ausrechne, so kriege ich natürlich schon  . Was mir aber nicht einleuchtet, ist, wieso die mit . Was mir aber nicht einleuchtet, ist, wieso die mit  , bzw. , bzw.  bezeichnet werden... bezeichnet werden... |
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 24. Apr 2007 22:10 Titel: dermarkus Verfasst am: 24. Apr 2007 22:10 Titel: |
 |
|
Die Zustände 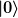 , , 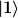 , ..., , ..., 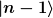 , , 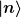 , ,  , ... sind die normierten Zustandsvektoren, die durch die Operatoren ineinander umgewandelt werden sollen. , ... sind die normierten Zustandsvektoren, die durch die Operatoren ineinander umgewandelt werden sollen.
| pfnuesel hat Folgendes geschrieben: | Wir wollen ja die Zustände  , bzw. , bzw.  normieren. normieren.
|
Fast. Genaugenommen wollen wir herausfinden, mit welchem Vorfaktor man den Aufsteigeoperator und den Absteigeoperator versehen muss, damit die so entstehenden Operatoren aus einem Zustand gerade den jeweils nächsthöheren bzw. nächstniedrigeren normierten Zustand machen. |
|
 |
Bruce
Anmeldungsdatum: 20.07.2004
Beiträge: 537
|
 Bruce Verfasst am: 24. Apr 2007 22:45 Titel: Bruce Verfasst am: 24. Apr 2007 22:45 Titel: |
 |
|
Vielleicht zum Verständnis noch das folgende:
Wenn a und b Zustände sind und O ein Operator ist, dann gilt stets in Dirac Notation:

wobei  der zu der zu 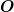 hermitesch adjungierte Operator ist. hermitesch adjungierte Operator ist.
Das heißt nun für das Problem, da  : :


Noch etwas zur Präzision der verwendeten Symbole und Begriffe: Die Ket's 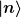
sind hier Elemente des Vektorraumes V der Zustände des betrachteten quantenmechanischen Systems
(harmonischer Oszillator?) und die Bra's  sind Elemente des zu V dualen Vektorraumes, sind Elemente des zu V dualen Vektorraumes,
welcher mit den linearen Funktionalen über V identisch ist.
Ket's sind also Vektoren und Bra's lineare Funktionale, d.h. lineare Abbildungen der Kets
auf den Grundkörper (hier komplexe Zahlen) des Vektorraumes V.
Gruß von Bruce |
|
 |
pfnuesel
Anmeldungsdatum: 04.11.2004
Beiträge: 248
Wohnort: Zürich
|
 pfnuesel Verfasst am: 25. Apr 2007 19:19 Titel: pfnuesel Verfasst am: 25. Apr 2007 19:19 Titel: |
 |
|
Vielen Dank nochmals für die Antworten.
So ganz klar ist's noch nicht, aber es wird von Tag zu Tag besser! 
Werd mich jetzt erstmals im Script weiterarbeiten und die Stelle später nochmals im Detail betrachten. |
|
 |
|
|
















