| Autor |
Nachricht |
Kelvin1994
Gast
|
 Kelvin1994 Verfasst am: 31. Okt 2021 23:45 Titel: Sind Lorentz-Tensoren überhaupt Tensoren? Kelvin1994 Verfasst am: 31. Okt 2021 23:45 Titel: Sind Lorentz-Tensoren überhaupt Tensoren? |
 |
|
Das mag nach einer dummen Frage klingen, aber ich hab da ein Verständnisproblem. In der Physik definiert man Tensoren häufig über das Transformationsverhalten bei einem Kartenwechsel (Koordinatentransformation).
In der SRT hat man als Mannigfaltigkeit den vierdimensionalen Minkowski-Raum.
Wenn man nun bspw ein kontravariantes Vektorfeld (oder genauer die Komponenten davon) betrachtet, gibt es bei bei einem Kartenwechsel

diese Beziehung:
 = \frac{\partial x'}{\partial x}v^\mu (x))
wobei x die Koordinaten bei der Karte  und x' die Koordinaten bei der Karte und x' die Koordinaten bei der Karte 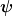 sind. sind.
Jetzt gilt diese Beziehung aber eigentlich für alle Kartenwechsel, während man in der SRT aber wohl nur Kartenwechsel die zur Lorentz- bzw Poincaré-Gruppe gehören, betrachtet. Schließlich geht es ja darum Gleichungen aufzustellen, die auf beiden Seiten Tensoren gleicher Stufe hat, so dass die Gleichungen im Falle eines Kartenwechsels ihre Form behalten und damit ihre Gültigkeit von der entsprechenden Karte unabhängig ist. Aber wenn es sich um Tensoren handeln soll, müssten diese Gleichungen dann auch ihre Form bei Kartenwechsel behalten, die nicht zur Poincaré-Gruppe gehören oder hab ich das falsch?
Ich komme aus einer Mathematiker-Perspektive und möchte ein bisschen Physik verstehen und bei der Physik versteh ich irgendwie manches nicht.
Ich versteh auch nicht warum man Tensoren über das Transformationsverhalten definiert. Einfacher verständlich fände ich es, wenn man Tensoren, wie in der Mathematik üblich, als Multilinearformen einführt und anschließend Basen und Komponenten einführt und dann das Transformationsverhalten untersucht. Mich verwirrt auch, dass man fast nie von den Mannigfaltigkeiten spricht, die man zugrunde legt.
Ich hoffe man kann mir die Physikersprache näher bringen. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 01. Nov 2021 07:32 Titel: Re: Sind Lorentz-Tensoren überhaupt Tensoren? index_razor Verfasst am: 01. Nov 2021 07:32 Titel: Re: Sind Lorentz-Tensoren überhaupt Tensoren? |
 |
|
| Kelvin1994 hat Folgendes geschrieben: |
Wenn man nun bspw ein kontravariantes Vektorfeld (oder genauer die Komponenten davon) betrachtet, gibt es bei bei einem Kartenwechsel

diese Beziehung:
 = \frac{\partial x'}{\partial x}v^\mu (x))
wobei x die Koordinaten bei der Karte  und x' die Koordinaten bei der Karte und x' die Koordinaten bei der Karte 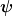 sind. sind.
Jetzt gilt diese Beziehung aber eigentlich für alle Kartenwechsel, während man in der SRT aber wohl nur Kartenwechsel die zur Lorentz- bzw Poincaré-Gruppe gehören, betrachtet. Schließlich geht es ja darum Gleichungen aufzustellen, die auf beiden Seiten Tensoren gleicher Stufe hat, so dass die Gleichungen im Falle eines Kartenwechsels ihre Form behalten und damit ihre Gültigkeit von der entsprechenden Karte unabhängig ist. Aber wenn es sich um Tensoren handeln soll, müssten diese Gleichungen dann auch ihre Form bei Kartenwechsel behalten, die nicht zur Poincaré-Gruppe gehören oder hab ich das falsch?
|
Dieses Transformationsgesetz gilt auch in der SRT unter beliebigen Koordinatentransformationen. Und man kann selbstverständlich auch andere Kartenwechsel betrachten als Lorentztransformationen, z.B. den Wechsel in ein lokales Ruhesystem eines konstant beschleunigten Beobachters. Die besondere Rolle der Lorentztransformation kommt aus dem Relativitätsprinzip, also der Aussage, daß die Lorentzgruppe (oder allgemeiner Poincaregruppe) eine Symmetrie der dynamischen Grundgleichungen ist. Das hat mit Kartenwechseln eigentlich gar nichts zu tun.
| Zitat: |
Ich komme aus einer Mathematiker-Perspektive und möchte ein bisschen Physik verstehen und bei der Physik versteh ich irgendwie manches nicht.
Ich versteh auch nicht warum man Tensoren über das Transformationsverhalten definiert. Einfacher verständlich fände ich es, wenn man Tensoren, wie in der Mathematik üblich, als Multilinearformen einführt und anschließend Basen und Komponenten einführt und dann das Transformationsverhalten untersucht.
|
Das kann man zum Glück in der Physik auch genauso tun. Und ich würde auch genau das empfehlen. Über die Frage wie man indizierten Größen ansehen kann, ob sie das "richtige" Transformationsverhalten haben, kann man ansonsten lange diskutieren. Ist zum Beispiel die Energie kein Skalar, weil es die 0-Komponente eines Vierervektors ist oder doch ein Skalar weil es ein Minkowskiprodukt zweier Vierervektoren ist. Noch schlimmer wird es bei dem Transformationsverhalten der "Christoffelsymbole". |
|
 |
Kelvin1994
Gast
|
 Kelvin1994 Verfasst am: 01. Nov 2021 09:34 Titel: Re: Sind Lorentz-Tensoren überhaupt Tensoren? Kelvin1994 Verfasst am: 01. Nov 2021 09:34 Titel: Re: Sind Lorentz-Tensoren überhaupt Tensoren? |
 |
|
| Zitat: | | Dieses Transformationsgesetz gilt auch in der SRT unter beliebigen Koordinatentransformationen. Und man kann selbstverständlich auch andere Kartenwechsel betrachten als Lorentztransformationen, z.B. den Wechsel in ein lokales Ruhesystem eines konstant beschleunigten Beobachters. Die besondere Rolle der Lorentztransformation kommt aus dem Relativitätsprinzip, also der Aussage, daß die Lorentzgruppe (oder allgemeiner Poincaregruppe) eine Symmetrie der dynamischen Grundgleichungen ist. Das hat mit Kartenwechseln eigentlich gar nichts zu tun. |
Nehmen wir als Beispiel mal die Minkowski-Gleichung.

Dabei ist  die Minkowki-Kraft oder Vierer-Kraft und die Minkowki-Kraft oder Vierer-Kraft und  die Vierer-Beschleunigung. Beides sollen kontravariante Vektoren sein. Nun kann ich einen beliebigen Kartenwechsel machen und erhalte danach die Gleichung die Vierer-Beschleunigung. Beides sollen kontravariante Vektoren sein. Nun kann ich einen beliebigen Kartenwechsel machen und erhalte danach die Gleichung

Dabei sind die gestrichenen Größen die Vektoren nach dem Kartenwechsel.
Also ist dann die Gleichung auch in beliebigen anderen Karten gültig, jedoch ist die Aussage der SRT doch, dass sie nur bei Kartenwechseln gültig ist, die in der Poincaré-Gruppe liegen. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 01. Nov 2021 09:56 Titel: Re: Sind Lorentz-Tensoren überhaupt Tensoren? index_razor Verfasst am: 01. Nov 2021 09:56 Titel: Re: Sind Lorentz-Tensoren überhaupt Tensoren? |
 |
|
| Kelvin1994 hat Folgendes geschrieben: |
Nehmen wir als Beispiel mal die Minkowski-Gleichung.

Dabei ist  die Minkowki-Kraft oder Vierer-Kraft und die Minkowki-Kraft oder Vierer-Kraft und  die Vierer-Beschleunigung. Beides sollen kontravariante Vektoren sein. Nun kann ich einen beliebigen Kartenwechsel machen und erhalte danach die Gleichung die Vierer-Beschleunigung. Beides sollen kontravariante Vektoren sein. Nun kann ich einen beliebigen Kartenwechsel machen und erhalte danach die Gleichung

Dabei sind die gestrichenen Größen die Vektoren nach dem Kartenwechsel. Also ist dann die Gleichung auch in beliebigen anderen Karten gültig, jedoch ist die Aussage der SRT doch, dass sie nur bei Kartenwechseln gültig ist, die in der Poincaré-Gruppe liegen. |
Nein, das stimmt so nicht. Du kannst natürlich jede beliebige Beziehung zwischen Tensoren in jeder beliebigen Karte ausdrücken. Das sagt überhaupt nichts über die Symmetrien der Gleichung aus.
Genauer gesagt: Du kannst zwar 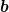 und und 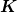 als Tangentialvektoren in einem fixen Ereignis betrachten und dann die Konsequenzen von Kartenwechseln untersuchen. Das führt genau auf den von dir genannten Zusammenhang zwischen gestrichenen und ungestrichenen Komponenten. als Tangentialvektoren in einem fixen Ereignis betrachten und dann die Konsequenzen von Kartenwechseln untersuchen. Das führt genau auf den von dir genannten Zusammenhang zwischen gestrichenen und ungestrichenen Komponenten.
Bei der Poincaresymmetrie geht es aber um etwas völlig anderes. Dort betrachtest du die Invarianz der Lösungsmenge von, sagen wir, der Differentialgleichung ) = m \ddot x(\tau)) . Die Symmetrie dieser Menge kann sehr wohl lediglich aus der Poincaregruppe bestehen, auch wenn K und . Die Symmetrie dieser Menge kann sehr wohl lediglich aus der Poincaregruppe bestehen, auch wenn K und  Tensoren (Vektoren) sind. Tensoren (Vektoren) sind.
Zuletzt bearbeitet von index_razor am 01. Nov 2021 11:05, insgesamt 2-mal bearbeitet |
|
 |
Kelvin1994
Gast
|
 Kelvin1994 Verfasst am: 01. Nov 2021 10:16 Titel: Kelvin1994 Verfasst am: 01. Nov 2021 10:16 Titel: |
 |
|
Aber ich dachte der Sinn, dass man Grundgleichungen in die tensorielle Form bringt, besteht darin, dass man daraus sofort die Kovarianz ablesen kann, da sich beide Seiten der Gleichung gleich transformieren. Deswegen bringt man doch auch die Maxwell-Gleichungen in eine Tensorform, um dann zu sagen, dass die Maxwellgleichungen forminvariant unter Lorentztransformation sind.
Sind also die Maxwellgleichungen, Minkowski-Gleichung usw forminvariant unter jedem Kartenwechsel, aber aus dieser Forminvarianz kann man nicht die Symmetrie ablesen?
Aber dann würde es doch gar nicht ausreichen eine Gleichung in eine Tensorform zu bringen, um lorentzinvarianz einer Theorie zu zeigen, aber das wird doch in der Literatur immer so gemacht, dachte ich. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 01. Nov 2021 10:53 Titel: index_razor Verfasst am: 01. Nov 2021 10:53 Titel: |
 |
|
| Kelvin1994 hat Folgendes geschrieben: |
Sind also die Maxwellgleichungen, Minkowski-Gleichung usw forminvariant unter jedem Kartenwechsel, aber aus dieser Forminvarianz kann man nicht die Symmetrie ablesen?
|
Ja, natürlich. Du hast doch selbst festgestellt, daß das Tensortransformationsgesetz für jeden beliebigen Kartenwechsel gilt. Wie soll daraus etwas spezielles über Lorentzsymmetrie folgen? Praktisch alle Gleichungen der klassischen Physik von der Newtonschen Mechanik bis zur Allgemeinen Realtivitätstheorie lassen sich als Beziehungen zwischen Tensoren auffassen. Aber diese Gleichungen besitzen natürlich nicht alle dieselbe Symmetrie. (Selbst die Symmetrigruppe der Maxwellgleichungen im Vakuum ist sogar größer als die Poincaregruppe und beinhaltet noch konforme Transformationen, die im Relativitätsprinzip aber keine Rolle spielen.) |
|
 |
Kelvin1994
Gast
|
 Kelvin1994 Verfasst am: 01. Nov 2021 11:19 Titel: Kelvin1994 Verfasst am: 01. Nov 2021 11:19 Titel: |
 |
|
Wie weist man denn dann nach, ob eine Gleichung eine Symmetrie bzgl Lorentztransformation hat?
In der Literatur begnügt man sich meistens damit die Gleichungen als Tensorgleichungen zu formulieren.
Mal angenommen ich führe eine Transformation von Koordinaten  nach Koordinaten nach Koordinaten 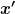 durch. durch.
Dann gilt für die Transformation Koordinatendifferential

Für die Vierergeschwindigkeit gilt

Wenn die Koordinatentransformation die Lorentztransformation ist, gilt

was aber unter anderen Transformationen nicht gelten kann, da  nur unter Lorentztransformationen invariant ist. nur unter Lorentztransformationen invariant ist.
Dann kann doch die Vierergeschwindigkeit sich nicht unter beliebigen transformationen wie ein Tensor transformieren.
Vielleicht versteh ich es besser, wenn du mir zeigst, wie man zeigt, dass die Minkowski-Gleichung nicht galilei invariant ist. Denn auch die Galilei Transformation müsste eine zulässige Transformation sein, nur dass halt die Gleichungen bzgl dieser Transformation in der SRT keine Symmetrien haben, aber wie jetzt gesagt wurde, hat die Minkowski-Gleichung dieselbe Form, vor und nach der Galileitransformation. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 01. Nov 2021 12:14 Titel: index_razor Verfasst am: 01. Nov 2021 12:14 Titel: |
 |
|
| Kelvin1994 hat Folgendes geschrieben: | Wie weist man denn dann nach, ob eine Gleichung eine Symmetrie bzgl Lorentztransformation hat?
|
Das ist ein bißchen als würdest du fragen, wie man nachweist, daß eine Funktion integrierbar ist. Für den Nachweis gibt es verschiedene Methoden. Welche davon praktisch ist (und ob überhaupt eine), hängt von der Gleichung ab. (Einen guten Überblick über die Methoden liefert m.E. Stephani, "Differential Equations, Their solution using symmetries".) Oder fragst du was die Definition einer Symmetrie ist?
| Zitat: |
In der Literatur begnügt man sich meistens damit die Gleichungen als Tensorgleichungen zu formulieren. |
Ehrlich gesagt bezweifle ich das. Kann es sein, daß du etwas falsch verstanden hast? Wird irgendwo behauptet, daß die Newtonschen Bewegungsgleichungen keine Tensorgleichungen sind oder daß sie lorentzinvariant sind? Die Literatur, die ich kenne, behauptet, daß Beschleunigung und Kraft Vektoren (also Tensoren) sind und daß die Newtonsche Mechanik galileiinvariant (nicht lorentzinvariant) ist.
| Zitat: |
Mal angenommen ich führe eine Transformation von Koordinaten  nach Koordinaten nach Koordinaten 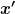 durch. durch.
Dann gilt für die Transformation Koordinatendifferential

Für die Vierergeschwindigkeit gilt

Wenn die Koordinatentransformation die Lorentztransformation ist, gilt

was aber unter anderen Transformationen nicht gelten kann, da  nur unter Lorentztransformationen invariant ist. Dann kann doch die Vierergeschwindigkeit sich nicht unter beliebigen transformationen wie ein Tensor transformieren. nur unter Lorentztransformationen invariant ist. Dann kann doch die Vierergeschwindigkeit sich nicht unter beliebigen transformationen wie ein Tensor transformieren.
|
Der Begriff "Vierergeschwindigkeit" ist praktisch die Definition von Tangentialvektor. Wenn du meinst für Tangentialvektoren auf einer Lorentzmannigfaltigkeit gelte das allgemeine Tensortransformationsgesetz, für Vierergeschwindigkeiten aber nicht, dann liegt hier irgendein grundlegendes Mißverständnis vor. Ich kann aber nicht genau sagen worin es besteht.
| Zitat: |
Vielleicht versteh ich es besser, wenn du mir zeigst, wie man zeigt, dass die Minkowski-Gleichung nicht galilei invariant ist.
Denn auch die Galilei Transformation müsste eine zulässige Transformation sein, nur dass halt die Gleichungen bzgl dieser Transformation in der SRT keine Symmetrien haben, aber wie jetzt gesagt wurde, hat die Minkowski-Gleichung dieselbe Form, vor und nach der Galileitransformation. |
Von derselben "Form" habe ich nicht gesprochen. Ich weiß nicht mal was die "Form" einer Gleichung genau sein soll. Ich habe nur von Symmetrien und dem grundlegenden Unterschied zu Kartenwechseln gesprochen. "Zulässig" als Kartenwechsel sind alle glatten Abbildungen, also auch Galileitransformationen. Das müßte vom mathematischen Standpunkt eigentlich einleuchten. Um die Symmetrie einer Gleichung zu untersuchen, muß man die abhängigen und unabhängigen Variablen festlegen. Das heißt man muß sagen, welche Funktionen u(x) als Lösungen in betracht kommen und dann irgendeine Beziehung zwischen x, u und Ableitungen von u nach x hinschreiben. Aus der der tautologischen Beziehung  kann man in der Hinsicht nicht viel ablesen. (In dieser Allgemeinheit könnte es sich ja sogar um eine Formulierung der Newtonschen Gleichung handeln.) kann man in der Hinsicht nicht viel ablesen. (In dieser Allgemeinheit könnte es sich ja sogar um eine Formulierung der Newtonschen Gleichung handeln.) |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 01. Nov 2021 13:57 Titel: Kelvin1995 Verfasst am: 01. Nov 2021 13:57 Titel: |
 |
|
Ja es gibt wohl irgendein Missverständnis und mir ist selber noch nicht klar worin das Missverständnis besteht.
Ich habe mal ein Beispielskript ergooglet. Dort wird es so dargestellt, wie ich es häufig lese
itp.uni-frankfurt.de/~gros/Vorlesungen/ED/Teil-VII.pdf
In Kapitel 18.7 auf Seite 173 werden Vierervektoren eingeführt. Kontravariante Vektoren werden dabei so eingeführt, dass sich die Komponenten unter Lorentztranformationen entsprechend transformieren. Warum legt man sich hier auf Lorentztransformationen fest, obwohl das angegebene Verhalten auf Seite 173 für jeden Kartenwechsel gilt, wenn es ein kontravarianter Vektor sein soll? Das wird häufig so formuliert, weshalb ich den Eindruck hatte als ob man "Tensoren" betrachtet, die nur bei Lorentztransformationen das "Tensortransformationsverhalten" zeigen.
In Kapitel 19 soll dann die Lorentz-Invarianz der Maxwellgleichungen nachgewiesen werden.
Am Ende von Seite 184 wird dann einfach die inhomogene Wellengleichung des Viererpotentials hingeschrieben. Man hat halt ne Tensorform und es wird dann einfach behauptet, dass diese Gleichung lorentzinvariant sei, aber ich sehe nicht, dass jetzt ganz konkret da noch irgendwas gemacht wird, um das nachzuweisen außer dass man halt die Gleichungen alle in Tensorform gebracht hat.
Ich habe grad auch nochmal in den Fließbach geschaut und da ist es ähnlich.
Nur um zu schauen ob wir vom selben reden, sag ich mal was ich unter einer Symmetrie einer DGL verstehe. Darunter verstehe ich eine Transformation, die Lösungen einer DGL auf Lösungen derselben DGL abbildet.
Letztlich müsste man doch dann zeigen, dass die transformierten Komponenten dieselbe DGL lösen wie die untransformierten Komponenten oder nicht? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 01. Nov 2021 19:09 Titel: index_razor Verfasst am: 01. Nov 2021 19:09 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | Ja es gibt wohl irgendein Missverständnis und mir ist selber noch nicht klar worin das Missverständnis besteht.
Ich habe mal ein Beispielskript ergooglet. Dort wird es so dargestellt, wie ich es häufig lese
itp.uni-frankfurt.de/~gros/Vorlesungen/ED/Teil-VII.pdf
In Kapitel 18.7 auf Seite 173 werden Vierervektoren eingeführt. Kontravariante Vektoren werden dabei so eingeführt, dass sich die Komponenten unter Lorentztranformationen entsprechend transformieren. Warum legt man sich hier auf Lorentztransformationen fest, obwohl das angegebene Verhalten auf Seite 173 für jeden Kartenwechsel gilt, wenn es ein kontravarianter Vektor sein soll?
|
Ich vermute weil dort Vektorkomponenten mit Koordinatendifferenzen identifiziert werden. Das ist ohnehin nur im Vektorraum sinnvoll, wenn man außerdem lineare Koordinatentransformationen betrachtet. Warum dann nicht gleich alle linearen Transformationen zugelassen sind, sondern nur isometrische, muß man wohl den Autor fragen. Aber unnötig ist diese Einschränkung in jedem Fall. Wenn man nicht klarstellt von welcher Art Vektorraum man redet, hängt jede Definition von "Vektor" ohnehin in der Luft. Und wenn man es klargestellt hat, kann man sich alle Transformationsgesetze selbst herleiten und benötigt dafür keine Spezialdefinition mehr.
| Zitat: |
Das wird häufig so formuliert, weshalb ich den Eindruck hatte als ob man "Tensoren" betrachtet, die nur bei Lorentztransformationen das "Tensortransformationsverhalten" zeigen. |
Ich glaube diese ganze Art der Definition ist letztlich sinnlos. Normalerweise verstehen Physiker nicht was Tensoren sind, weil sie diese Definition verstehen, sondern weil ihnen jemand gesagt hat: "Dies Ding hier ist ein Vektor, dies ein Kovektor, dies ist gar kein Tensor, ..." etc. zusammen mit Regeln, durch welche Operationen man aus Tensoren weitere Tensoren zu bilden hat. So macht es dieses Skript auch.
Zum Beispiel wären nach der Definition aus dem Skript auch die Zusammenhangskoeffizienten Tensoren. Physiker "wissen" aber normalerweise, daß dies keine Tensoren sind, und zwar wegen des Transformationsgesetzes

was für Lorentztransformationen aber genauso aussieht, wie das Tensortransformationsgesetz (sogar für alle umkehrbaren linearen Transformationen).
| Zitat: |
In Kapitel 19 soll dann die Lorentz-Invarianz der Maxwellgleichungen nachgewiesen werden.
Am Ende von Seite 184 wird dann einfach die inhomogene Wellengleichung des Viererpotentials hingeschrieben. Man hat halt ne Tensorform und es wird dann einfach behauptet, dass diese Gleichung lorentzinvariant sei, aber ich sehe nicht, dass jetzt ganz konkret da noch irgendwas gemacht wird, um das nachzuweisen außer dass man halt die Gleichungen alle in Tensorform gebracht hat.
|
Die restlichen Schritte sind eher implizit. Wenn man es mit einer Differentialgleichung der Form
, \partial_\mu T^{c\cdots}_{d\cdots}(x), \cdots) = 0\qquad (1))
für ein Tensorfeld T zu tun hat. Und wenn diese Gleichung unter Elementen  einer speziellen, linearen Transformationgruppe abgebildet wird auf einer speziellen, linearen Transformationgruppe abgebildet wird auf
, \partial_{\bar \mu} T^{\bar c\cdots}_{\bar d\cdots}(x), \cdots) = (\Lambda^{-1})^{a}_{\bar a}\cdots \Lambda^{\bar b}_b \cdots F^{\bar a\cdots }_{\bar b\dots }(x^\mu, T^{c\cdots}_{d\cdots}(x), \partial_\mu T^{c\cdots}_{d\cdots}(x), \cdots),\qquad (2))
dann ist diese Gleichung natürlich invariant unter  . .
Die unterschiedlichen Bedingungen werden oft vollkommen durcheinander geworfen. Laut Gl. (1) handelt es sich um eine Beziehug zwischen Tensoren. Damit gelten natürlich die üblichen Transformationsgesetze unter beliebigen Kartenwechseln für T und seine Ableitungen. Aber die Invarianzbedingung (2) gilt natürlich im allgemeinen nicht für alle diese Transformationen, sondern nur für eine spezielle Klasse  . Die Invarianzbedingung hat aber nicht das geringste mit der Frage zu tun ob irgendeine der beteiligten Größen selbst ein Tensor ist. Der einzige Zusammenhang zwischen (2) und dem Tensortransformationsgesetz besteht darin, daß man für konkretes . Die Invarianzbedingung hat aber nicht das geringste mit der Frage zu tun ob irgendeine der beteiligten Größen selbst ein Tensor ist. Der einzige Zusammenhang zwischen (2) und dem Tensortransformationsgesetz besteht darin, daß man für konkretes  normalerweise die Gültigkeit von (2) leicht prüfen kann, wenn die abhängigen Größen Tensoren sind. Aber mit der Definition von Tensoren hat das nichts zu tun. normalerweise die Gültigkeit von (2) leicht prüfen kann, wenn die abhängigen Größen Tensoren sind. Aber mit der Definition von Tensoren hat das nichts zu tun.
| Zitat: |
Nur um zu schauen ob wir vom selben reden, sag ich mal was ich unter einer Symmetrie einer DGL verstehe. Darunter verstehe ich eine Transformation, die Lösungen einer DGL auf Lösungen derselben DGL abbildet.
|
Ja, das verstehe ich auch darunter.
| Zitat: |
Letztlich müsste man doch dann zeigen, dass die transformierten Komponenten dieselbe DGL lösen wie die untransformierten Komponenten oder nicht? |
Ja, genau das muß man zeigen, z.B. indem man die Gültigkeit von (2) prüft.
Zuletzt bearbeitet von index_razor am 02. Nov 2021 16:17, insgesamt 2-mal bearbeitet |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 01. Nov 2021 19:49 Titel: Kelvin1995 Verfasst am: 01. Nov 2021 19:49 Titel: |
 |
|
Hallo erstmal danke, dass du dir die Mühe machst mich dabei zu unterstützen zu einem besseren Verständnis zu gelangen. So langsam lichtet es sich, hoffe ich jedenfalls.
Bei mir ist es so, dass ich meine die mathematischen Definitionen, Begrifflichkeiten usw aus der Differentialgeometrie verstanden zu haben, aber ich habe Probleme damit diese Begriffe auf die Physik zu übertragen und in vielen Physikbüchern, die ich gelesen habe, wird es halt ähnlich dargestellt wie im Skript. Im Fließbach zum Beispiel, ist es nicht viel anders und das führt bei mir zur Verwirrung.
Kannst du eine bestimmte Literatur empfehlen in der dies stringent dargestellt wird? Ich hätte auch gerne detaillierte konkrete Beispielrechnungen, weil ich habe das Gefühl, dass in der Literatur häufig einige Details überschlagen werden. Und wie du sagtest wird häufig suggeriert, dass (1) bereits (2) impliziert. Vor diesem Thread bin ich wirklich nach dem Lesen einiger Literatur davon ausgegangen, dass das Ziel immer ist die Gleichungen in die Form von (1) zu bringen und dann ist man halt fertig. Also ist der Sinn davon die Gleichungen in die Form (1) zu bekommen, weil man in dieser Form (2) leichter zeigen kann?
Das einfachste Beispiel, welches mir einfällt anhand dessen man dies untersuchen kann, wäre die Bewegungsgleichung für ein kräftefreies Teilchen

Diese Gleichung müsste doch Lorentz-Invariant aber nicht galilei-invariant sein oder? Wenn ich jetzt die Lorentz-Invarianz zeigen möchte, würde ich das jetzt so machen
Es gibt ein Bezugssystem indem  gilt. In diesem Bezugssystem haben alle Größen im folgenden keinen Strich und in einem lorentztransformierten System sind die Größen mit einem Strich versehen. Dann folgt: gilt. In diesem Bezugssystem haben alle Größen im folgenden keinen Strich und in einem lorentztransformierten System sind die Größen mit einem Strich versehen. Dann folgt:

Also gilt die Gleichung auch im transformiertem System. Ist das soweit richtig? Meine Frage ist jetzt, was mich daran hindert, exakt die gleiche Rechnung mit einer Galileitransformation durchzuführen. Auch bei einer Galileitransformation ist die Transformation konstant bzgl der Ableitung und ich kann sie aus dem Differential ziehen.
Und dann hätte ich noch die Frage, was man genau unter Forminvarianz versteht. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Nov 2021 11:25 Titel: index_razor Verfasst am: 02. Nov 2021 11:25 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: |
Bei mir ist es so, dass ich meine die mathematischen Definitionen, Begrifflichkeiten usw aus der Differentialgeometrie verstanden zu haben, aber ich habe Probleme damit diese Begriffe auf die Physik zu übertragen und in vielen Physikbüchern, die ich gelesen habe, wird es halt ähnlich dargestellt wie im Skript. Im Fließbach zum Beispiel, ist es nicht viel anders und das führt bei mir zur Verwirrung. Kannst du eine bestimmte Literatur empfehlen in der dies stringent dargestellt wird?
|
Was genau? Dirschmid, "Tensoren und Felder" enthält einen mathematischen Abriß der speziellen und allgemeinen Relativitätstheorie und eine kovariante Formulierung der Newtonschen Mechanik. Dort geht es allerdings nicht um Symmetrien. Dazu siehe z.B. das Buch von Stephani weiter oben.
| Zitat: |
Ich hätte auch gerne detaillierte konkrete Beispielrechnungen, weil ich habe das Gefühl, dass in der Literatur häufig einige Details überschlagen werden. Und wie du sagtest wird häufig suggeriert, dass (1) bereits (2) impliziert. Vor diesem Thread bin ich wirklich nach dem Lesen einiger Literatur davon ausgegangen, dass das Ziel immer ist die Gleichungen in die Form von (1) zu bringen und dann ist man halt fertig.
|
Wenn das Ziel ist, die Invarianz der Gleichung unter einer Klasse linearer Transformationen zu zeigen, ist das auch oft die einzige Schwierigkeit. Ich dachte zuerst es geht dir in erster Linie um die Definition des Tensorbegriffs und seine Beziehung zu allgemeinen Kartenwechseln.
| Zitat: |
Also ist der Sinn davon die Gleichungen in die Form (1) zu bekommen, weil man in dieser Form (2) leichter zeigen kann?
|
Ja, genau. Nimm als Beispiel die Wellengleichung  : Für lineares : Für lineares  kann man einfach alles vor die Ableitungen ziehen. Das ist der erste Schritt. Dann fehlt nur noch kann man einfach alles vor die Ableitungen ziehen. Das ist der erste Schritt. Dann fehlt nur noch  , was bis auf den Faktor C genau die definierende Eigenschaft der Lorentztransformation ist. Der transformierte Differentialoperator lautet also , was bis auf den Faktor C genau die definierende Eigenschaft der Lorentztransformation ist. Der transformierte Differentialoperator lautet also
^{\bar a}_{a}\cdots \Lambda^b_{\bar b}\cdots C g^{\mu\nu}\partial_\mu\partial_\nu T^{a\cdots}_{b\cdots},)
was genau für die Funktionen T verschwindet, für die auch ursprüngliche Gleichung verschwindet. Also haben wir gezeigt, daß die Symmetrien der Wellengleichung die Lorentztransformationen enthalten (C=1).
| Zitat: |
Das einfachste Beispiel, welches mir einfällt anhand dessen man dies untersuchen kann, wäre die Bewegungsgleichung für ein kräftefreies Teilchen

Diese Gleichung müsste doch Lorentz-Invariant aber nicht galilei-invariant sein oder? |
Das kann man so nicht sagen. Die Gleichung beschreibt lediglich eine Gerade. Sie sollte invariant unter allen affinen Transformationen  \mapsto (\Lambda x + v\tau + c, \alpha \tau + \beta), \ \alpha\neq 0) sein. Und das ist auch der Fall. Offensichtlich ist sein. Und das ist auch der Fall. Offensichtlich ist
)
und

(Man kann das auch so sehen: das Trägheitsprinzip legt nur fest, daß die Raumzeit eine affine Struktur hat. Aber ob es sich um eine Lorentz- oder eine galileische Mannigfaltigkeit handelt, legt es nicht fest.)
| Zitat: |
Wenn ich jetzt die Lorentz-Invarianz zeigen möchte, würde ich das jetzt so machen
Es gibt ein Bezugssystem indem  gilt. In diesem Bezugssystem haben alle Größen im folgenden keinen Strich und in einem lorentztransformierten System sind die Größen mit einem Strich versehen. Dann folgt: gilt. In diesem Bezugssystem haben alle Größen im folgenden keinen Strich und in einem lorentztransformierten System sind die Größen mit einem Strich versehen. Dann folgt:

Also gilt die Gleichung auch im transformiertem System. Ist das soweit richtig? Meine Frage ist jetzt, was mich daran hindert, exakt die gleiche Rechnung mit einer Galileitransformation durchzuführen. Auch bei einer Galileitransformation ist die Transformation konstant bzgl der Ableitung und ich kann sie aus dem Differential ziehen. |
Ganz genau. Nichts hindert dich. Siehe oben.
| Zitat: |
Und dann hätte ich noch die Frage, was man genau unter Forminvarianz versteht. |
Darunter würde ich den Spezialfall von Bedingung (2) verstehen
 = F^{a\cdots}_{b\cdots}(x, T^{c\cdots }_{d\cdots}, \partial_{ \mu}T^{ c\cdots }_{ d\cdots}, \cdots)) . .
Es bedeutet also soviel wie Invarianz der Operatoren  unter der betrachteten Klasse von Transformationen, die hier die ungestrichenen in die gestrichenen Größen überführen. Ich weiß aber nicht, ob die Verwendung des Begriffs einheitlich ist. "Forminvarianz" ist ein etwas nebulöses Konzept. unter der betrachteten Klasse von Transformationen, die hier die ungestrichenen in die gestrichenen Größen überführen. Ich weiß aber nicht, ob die Verwendung des Begriffs einheitlich ist. "Forminvarianz" ist ein etwas nebulöses Konzept. |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 02. Nov 2021 14:53 Titel: Kelvin1995 Verfasst am: 02. Nov 2021 14:53 Titel: |
 |
|
Danke das hat mir sehr weitergeholfen. Ich denke jetzt verstehe ich es.
Es ist jetzt aber noch eine Folgefrage aufgetreten.
In der physikalischen Literatur lese ich häufig von den Begriffen "passive Transformation" und "aktive Transformation".
So wie ich das verstehe, ist eine passive Transformation ein Kartenwechsel und bei einer aktiven Transformation wechselt man die Karte nicht, sondern transformiert die entsprechenden Vektoren, Kurven oder was auch immer. Ist das richtig?
Wann muss man denn was betrachten? Beim Noether-Theorem betrachtet man doch immer aktive Transformationen oder? Spricht man in beiden Fällen von Symmetrien einer DGL, also wenn man passive Transformationen und wenn man aktive Transformationen betrachtet?
Bezieht sich die Forderung nach Lorentz-Invarianz immer auf Kartenwechsel/passive Transformationen oder auch auf aktive Transformationen? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Nov 2021 08:29 Titel: index_razor Verfasst am: 03. Nov 2021 08:29 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: |
In der physikalischen Literatur lese ich häufig von den Begriffen "passive Transformation" und "aktive Transformation".
So wie ich das verstehe, ist eine passive Transformation ein Kartenwechsel und bei einer aktiven Transformation wechselt man die Karte nicht, sondern transformiert die entsprechenden Vektoren, Kurven oder was auch immer. Ist das richtig?
|
Ja, eine passive Transformation ist ein Kartenwechsel. Eine aktive Transformation ist eine Abbildung  der zugrundeliegenden Mannigfaltigkeit. Daraus ergeben sich die Transformationen von Vektoren als Differential (Pushforward) und die Transformationen von Kovektoren und skalaren Funktionen als Rücktransport (Pullback) von der zugrundeliegenden Mannigfaltigkeit. Daraus ergeben sich die Transformationen von Vektoren als Differential (Pushforward) und die Transformationen von Kovektoren und skalaren Funktionen als Rücktransport (Pullback) von  . .
| Zitat: |
Wann muss man denn was betrachten?
|
Das ist zunächst mal oft eine Frage des Geschmacks. Denn es gehört (sofern alle folgenden Verkettungen definiert sind) zu jeder Abbildung  und jeder Karte und jeder Karte 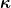 auch der Kartenwechsel auch der Kartenwechsel  , d.h. die Koordinaten des transformierten Punktes werden interpretiert als neue Koordinaten desselben Punktes. , d.h. die Koordinaten des transformierten Punktes werden interpretiert als neue Koordinaten desselben Punktes.
Und umgekehrt gehört zu einem Kartenwechsel  die Transformation die Transformation  , d.h. die neuen Koordinaten jedes Punktes werden interpretiert als die alten Koordinaten eines neuen Punktes. , d.h. die neuen Koordinaten jedes Punktes werden interpretiert als die alten Koordinaten eines neuen Punktes.
Da in der Physikerliteratur oft in Koordinaten gerechnet wird, sieht man den Unterschied zwischen aktiven und passiven Transformationen gar nicht.
Abgesehen davon ist die natürlichste Interpretation von Symmetrietransformationen als aktive Transformation auf einer geeigneten Mannigfaltigkeit. (Für Differentialgleichungen eine Mannigfaltigkeit von n-Jets.) Koordinatentransformationen erfüllen z.B. den Zweck, die Generatoren der Symmetrietransformation auf eine enfachere Form zu bringen, z.B. die Standardform  . .
| Zitat: |
Beim Noether-Theorem betrachtet man doch immer aktive Transformationen oder? Spricht man in beiden Fällen von Symmetrien einer DGL, also wenn man passive Transformationen und wenn man aktive Transformationen betrachtet?
Bezieht sich die Forderung nach Lorentz-Invarianz immer auf Kartenwechsel/passive Transformationen oder auch auf aktive Transformationen? |
Das Noether-Theorem behandelt einen Spezialfall von Symmetrien von Differentialgleichungen, nämlich solchen, die gleichzeitig Symmetrien einer Wirkung sind. Es gehört also in denselben Zusammenhang wie die Symmetrien von Differentialgleichungen. Dorthin gehört auch die Forderung nach Lorentz-Invarianz.
Auch die Rolle von aktiven und passiven Transformationen ist in allen Fällen dieselbe. Erstere definieren die Symmetrietransformationen (mittels Prolongation auf einen Jet-Raum), letztere wählt man unter pragmatischen Gesichtspunkten um z.B. die Form der Generatoren zu vereinfachen. |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 05. Nov 2021 08:15 Titel: Kelvin1995 Verfasst am: 05. Nov 2021 08:15 Titel: |
 |
|
Mir ist jetzt doch noch etwas unklar.
Betrachten wir als Beispiel mal die inhomogenen Maxwellgleichungen

Dabei ist F der elektromagnetische Feldstärke Tensor und enthält somit Ableitungen des Viererpotentials.
Es handelt sich hierbei also um eine Differentialgleichung des Viererpotentials.
Nun transformiere ich diese gleichung mittels einer Lorentztransformation
=0)
In diesem Fall lösen aber die transformierten Komponenten des Viererpotentials gar nicht dieselbe DGL wie die untransformierten Komponenten, da die Viererstromdichte sich auch transformiert und in der transformierten DGL hat sich damit der inhomogene Teil geändert, aber die Maxwell gleichungen müssen natürlich eine Symmetrie bzgl Lorentztransformation haben und Symmetrie würde doch bedeuten, dass die transformierten Komponenten des Viererpotentials Lösungen derselben DGL wie die untransformierten Komponenten sind. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
 TomS Verfasst am: 05. Nov 2021 11:46 Titel: TomS Verfasst am: 05. Nov 2021 11:46 Titel: |
 |
|
Das ist doch gerade der wesentliche Punkt der Symmetrie.
Du kannst F aus j durch Lösen der DGL im ursprünglichen Koordinatensystem bestimmen und dann sowohl F als auch j ins neue Koordinatensystem transformieren.
Oder du transformierst zuerst j ins neue Koordinatensystem und löst die DGL für das F im neue Koordinatensystem.
Beide Wege führen zum selben F.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 05. Nov 2021 12:15 Titel: Kelvin1995 Verfasst am: 05. Nov 2021 12:15 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Das ist doch gerade der wesentliche Punkt der Symmetrie.
Du kannst F aus j durch Lösen der DGL im ursprünglichen Koordinatensystem bestimmen und dann sowohl F als auch j ins neue Koordinatensystem transformieren.
Oder du transformierst zuerst j ins neue Koordinatensystem und löst die DGL für das F im neue Koordinatensystem.
Beide Wege führen zum selben F. |
Hallo TomS
Danke für die Antwort.
Mir ist schon irgendwie klar, dass man auf beiden Wege dieselben Fs bekommt. Ich kann das nur nicht mit der Definition in Einklang bringen, dass eine Transformation eine Symmetrie einer DGL ist, wenn die Transformation Lösungen der DGL auf Lösungen derselben DGL abbildet.
Denn wenn ich das j mit transformiere, habe ich ja nicht mehr dieselbe DGL, für die transformierten Fs bzw dem transformiertem Viererpotential.
Mal ein Beispiel. Wenn ich eine DGL habe wie
y''+y=x²
jetzt transformiere ich x nach u und y nach z(u) und erhalten
z''+z=u²
wobei jetzt die striche Ableitungen nach u sind. Das wäre für mich eine Symmetrie, da es eigentlich immer noch dieselbe DGL ist, aber wenn ich nach der transformation sowas erhalte wie
z''+z=2*u. dann wäre das für mich keine symmetrie mehr, da die DGL eine andere ist.
Ich habe irgendwo ein grundlegendes Verständnisproblem, ist aber halt schwierig rauszufinden woran es hapert. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 05. Nov 2021 12:38 Titel: index_razor Verfasst am: 05. Nov 2021 12:38 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | Nun transformiere ich diese gleichung mittels einer Lorentztransformation
=0)
In diesem Fall lösen aber die transformierten Komponenten des Viererpotentials gar nicht dieselbe DGL wie die untransformierten Komponenten
|
Müssen sie auch nicht. Nur die gekoppelten Gleichungen für Felder und Materie müssen dieselben sein. Die Gleichung, die du hingeschrieben hast, ist für sich allein genommen und für beliebiges  natürlich nicht lorentzinvariant. Aber sie ist auch nicht vollständig. Du hast zwar richtigerweise den Quellterm mittransformiert, aber vermutlich aus den falschen Gründen. Nämlich: natürlich nicht lorentzinvariant. Aber sie ist auch nicht vollständig. Du hast zwar richtigerweise den Quellterm mittransformiert, aber vermutlich aus den falschen Gründen. Nämlich:
| Zitat: |
da die Viererstromdichte sich auch transformiert und in der transformierten DGL hat sich damit der inhomogene Teil geändert,
|
Du sagst das so, als wäre es offensichtlich. Versuche mal zu begründen, warum du die Viererstromdichte transformiert hast. Du scheinst dir wieder einfach alle Tensorgrößen aus der Gleichung zu picken und das Tensortransformationsgesetz anzuwenden. Das hat aber, wie gesagt, nichts mit den Symmetrien der Gleichung zu tun.
Hier nochmal deine eigene Definition von Symmetrie: "[Unter Symmetrie] verstehe ich eine Transformation, die Lösungen einer DGL auf Lösungen derselben DGL abbildet.". Was sind die Lösungen dieser Gleichung und wie werden sie transformiert? Wie kommst du darauf, daß die obige Gleichung lorentzinvariant ist?
| Zitat: |
aber die Maxwell gleichungen müssen natürlich eine Symmetrie bzgl Lorentztransformation haben und Symmetrie würde doch bedeuten, dass die transformierten Komponenten des Viererpotentials Lösungen derselben DGL wie die untransformierten Komponenten sind. |
Wie untersuchen wir die Symmetrien der inhomogenen Maxwellgleichungen? Indem wir die Gleichungen für die Materie einbeziehen. Betrachten wir z.B. ein einzelnes Teilchen in EM-Feld, dann ist
 = q\int \dot z^\nu \delta(x - z^\lambda(\tau))\dd\tau)
 = qF^{\mu\nu}(z(\tau)) g_{\nu\lambda}\dot z^\lambda(\tau))
(Die homogenen Gl. sehe ich als trivial erfüllt an, wenn wir F durch Potentiale ausdrücken.) Hier haben wir also die unabhängigen Variablen x und 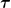 und die abhängigen Variablen und die abhängigen Variablen ) , , ) . Nun transformieren wir die Funktionen . Nun transformieren wir die Funktionen ) und und ) , setzten sie in die gekoppelten Gleichungen ein und prüfen dadurch ob sie sie wieder lösen. , setzten sie in die gekoppelten Gleichungen ein und prüfen dadurch ob sie sie wieder lösen.
Kleine Abschweifung: Der Punkt, über den du hier gestolpert bist, hat übrigens eine Analogie in der Newtonschen Mechanik. Es scheinen viele die Galileiinvarianz der Theorie für eine triviale Folge aus der "Definition der Kraft"  zu halten. Das Argument geht so: Unter zu halten. Das Argument geht so: Unter  ist offenbar die Beschleunigung invariant ist offenbar die Beschleunigung invariant  . Aber . Aber  per Definition. Also scheint auch F' = F zu folgen. (Wer ein Faible für besonders wasserdichte Argumente hat, schließt dann noch die "Lücke" m'=m mit dem Hinweis, daß die Masse ein "Skalar" ist.) Aber natürlich kann höchstens eine der Gleichungen per Definition. Also scheint auch F' = F zu folgen. (Wer ein Faible für besonders wasserdichte Argumente hat, schließt dann noch die "Lücke" m'=m mit dem Hinweis, daß die Masse ein "Skalar" ist.) Aber natürlich kann höchstens eine der Gleichungen  oder oder  eine "Definition" sein, da F ja normalerweise von x abhängt und diese Abhängigkeit das Transformationsgesetz von F festlegt. eine "Definition" sein, da F ja normalerweise von x abhängt und diese Abhängigkeit das Transformationsgesetz von F festlegt.
Demselben Argument begegnet man nicht nur für Boosts, sondern auch für Rotationen R: Beschleunigung ist ein Vektor, Kraft ist ein Vektor (Masse ein Skalar), also gilt  genau dann wenn genau dann wenn  . (Ich vermute, daß deiner Transformation der inhomogenen Maxwellgleichung ein ähnliches Argument zugrunde liegt.) Aber F' = RF kann nur dann gelten,wenn F die richtige x-Abhängigkeit hat. . (Ich vermute, daß deiner Transformation der inhomogenen Maxwellgleichung ein ähnliches Argument zugrunde liegt.) Aber F' = RF kann nur dann gelten,wenn F die richtige x-Abhängigkeit hat.
Zuletzt bearbeitet von index_razor am 05. Nov 2021 12:52, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 05. Nov 2021 12:48 Titel: index_razor Verfasst am: 05. Nov 2021 12:48 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: |
Mal ein Beispiel. Wenn ich eine DGL habe wie
y''+y=x²
jetzt transformiere ich x nach u und y nach z(u) und erhalten
z''+z=u²
wobei jetzt die striche Ableitungen nach u sind. Das wäre für mich eine Symmetrie, da es eigentlich immer noch dieselbe DGL ist, aber wenn ich nach der transformation sowas erhalte wie
z''+z=2*u. dann wäre das für mich keine symmetrie mehr, da die DGL eine andere ist.
Ich habe irgendwo ein grundlegendes Verständnisproblem, ist aber halt schwierig rauszufinden woran es hapert. |
Das klingt im Prinzip schon richtig was du schreibst. Ich glaube dir ist nur noch nicht die präzise Definition von "Symmetrie" klar. Du sagst zwar korrekterweise, daß eine Symmetrie Lösungen auf Lösungen der Differentialgleichungen abbilden muß. Aber was bedeutet das eigentlich formal? |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 05. Nov 2021 14:22 Titel: Kelvin1995 Verfasst am: 05. Nov 2021 14:22 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Müssen sie auch nicht. Nur die gekoppelten Gleichungen für Felder und Materie müssen dieselben sein. Die Gleichung, die du hingeschrieben hast, ist für sich allein genommen und für beliebiges  natürlich nicht lorentzinvariant. Aber sie ist auch nicht vollständig. Du hast zwar richtigerweise den Quellterm mittransformiert, aber vermutlich aus den falschen Gründen. Nämlich: natürlich nicht lorentzinvariant. Aber sie ist auch nicht vollständig. Du hast zwar richtigerweise den Quellterm mittransformiert, aber vermutlich aus den falschen Gründen. Nämlich:
|
Ich könnte ja statt der Viererstromdichte die Kopplung des EM-Feldes an das Dirac-Feld betrachten, also sprich ich betrachte die Lagrangedichte der Quantenelektrodynamik. Die entsprechenden Bewegungsgleichungen wären doch dann sicherlich Lorentzinvariant oder? Es handelt sich ja bei der Beschreibung mit der Viererstromdichte um eine effektive (unvollständige) Beschreibung der EM-Wechselwirkung. Wenn ich jetzt einen konkreten Ausdruck für j hinschreiben würde, der sich aus Diracfeldern ergibt, könnte ich dann zeigen, dass es lorentzinvariant ist?
Nun ist es doch in der Literatur häufig so, dass man gerne die lorentzinvarianz der Maxwell-Gleichungen zeigen möchte und dazu die Maxwellgleichungen in die sogenannte kovariante Form bringt. Man hat dann letztlich zwei Gleichungen. Eine homogene und eine inhomogene Gleichung. Kovarianz bedeutet doch einfach nur, dass sich beide Seiten bei einem Kartenwechsel gleich transformieren oder? Über lorentzinvarianz sagt das ja noch nichts aus.
Ich hab grad mal im Jackson geblättert. Dort steht:
| Zitat: |
Bereits vor der Formulierung der speziellen Relativitätstheorie zeigten Lorentz und Poincaré, dass die Gleichungen der Elektrodynamik unter Lorentztransformationen forminvariant sind. Diese Forminvarianz oder auch Kovarianz , wie sie z.B. die Maxwell-Lorentzsche Gleichung für die Kraft auf ein geladenes Teilchen ...
|
Hier wird zunächst forminvarianz und kovarianz gleichgesetzt, wobei ich dachte dass es nicht dasselbe sei.
In dem ganzen Kapitel werden dann die Maxwell-Gleichungen in die kovariante Form gebracht. Es wird auch von der "Forderung nach lorentzkovarianz" gesprochen. Was soll denn Lorentzkovarianz sein? Ich versteh darunter, dass sich beide Seiten der Gleichung unter lorentztransformation gleich transformieren, aber wenn auf beiden Seiten der Gleichung Tensoren gleicher Stufe sind, sollte dies doch nicht nur für lorentztransformationen der Fall sein.
Und wenn ich in anderen Büchern schaue, ist es wieder anders dargestellt.
| Zitat: | Kleine Abschweifung: Der Punkt, über den du hier gestolpert bist, hat übrigens eine Analogie in der Newtonschen Mechanik. Es scheinen viele die Galileiinvarianz der Theorie für eine triviale Folge aus der "Definition der Kraft"  zu halten. Das Argument geht so: Unter zu halten. Das Argument geht so: Unter  ist offenbar die Beschleunigung invariant ist offenbar die Beschleunigung invariant  . Aber . Aber  per Definition. Also scheint auch F' = F zu folgen. (Wer ein Faible für besonders wasserdichte Argumente hat, schließt dann noch die "Lücke" m'=m mit dem Hinweis, daß die Masse ein "Skalar" ist.) Aber natürlich kann höchstens eine der Gleichungen per Definition. Also scheint auch F' = F zu folgen. (Wer ein Faible für besonders wasserdichte Argumente hat, schließt dann noch die "Lücke" m'=m mit dem Hinweis, daß die Masse ein "Skalar" ist.) Aber natürlich kann höchstens eine der Gleichungen  oder oder  eine "Definition" sein, da F ja normalerweise von x abhängt und diese Abhängigkeit das Transformationsgesetz von F festlegt. eine "Definition" sein, da F ja normalerweise von x abhängt und diese Abhängigkeit das Transformationsgesetz von F festlegt.
|
Kann man denn die Galilei-invarianz zeigen, wenn man die x-Abhängigkeit der Kraft wie folgt einschränkt
)
Das soll eine zweiteilchen_Wechselwirkung repräsentieren. v sind die geschwindigkeiten.
Dann müsste ja wegen =F(x_2-x_1, v_2-v_1)) die galilei invarianz offensichtlich sein, wobei die gestrichenen Größen die galileitransformierten Koordinaten sind. die galilei invarianz offensichtlich sein, wobei die gestrichenen Größen die galileitransformierten Koordinaten sind.
Wäre dann die galilei invarianz eigentlich verletzt, wenn ich ein externes Kraftfeld nehme. Was ich mir dadurch erkläre, dass so eine Beschreibung unvollständig ist, da eigentlich auch ein externes Feld durch paarweise Wechselwirkungen zustande kommen.
Ich habe jedenfalls den Eindruck, dass die Literatur in diesem Bereich sehr uneinheitlich und teils irreführend ist. Es kann natürlich auch an mir liegen, dass ich einfach ein kognitives Problem damit habe.
 |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 05. Nov 2021 15:54 Titel: index_razor Verfasst am: 05. Nov 2021 15:54 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Müssen sie auch nicht. Nur die gekoppelten Gleichungen für Felder und Materie müssen dieselben sein. Die Gleichung, die du hingeschrieben hast, ist für sich allein genommen und für beliebiges  natürlich nicht lorentzinvariant. Aber sie ist auch nicht vollständig. Du hast zwar richtigerweise den Quellterm mittransformiert, aber vermutlich aus den falschen Gründen. Nämlich: natürlich nicht lorentzinvariant. Aber sie ist auch nicht vollständig. Du hast zwar richtigerweise den Quellterm mittransformiert, aber vermutlich aus den falschen Gründen. Nämlich:
|
Ich könnte ja statt der Viererstromdichte die Kopplung des EM-Feldes an das Dirac-Feld betrachten, also sprich ich betrachte die Lagrangedichte der Quantenelektrodynamik. Die entsprechenden Bewegungsgleichungen wären doch dann sicherlich Lorentzinvariant oder? Es handelt sich ja bei der Beschreibung mit der Viererstromdichte um eine effektive (unvollständige) Beschreibung der EM-Wechselwirkung. Wenn ich jetzt einen konkreten Ausdruck für j hinschreiben würde, der sich aus Diracfeldern ergibt, könnte ich dann zeigen, dass es lorentzinvariant ist?
|
Ja, genau. Das macht ja auch gerade den Unterschied aus. Wenn der Quellterm auf der rechten Seite die Stromdichte des Fermionenfeldes ist, dann ist das vollständige System der gekoppelten Maxwell- und Diracgleichung auch lorentzinvariant. Wenn du den Strom einfach als externes Feld betrachtest und nicht als dynamischen Freiheitsgrad, dann folgt auch nicht ohne weiteres die Lorentzinvarianz der inhomogenen Maxwellgleichungen. Das ist ja auch klar, schließlich kannst du das EM-Feld auch mit nichtrelativistischen Gleichungen verbinden. Dann kriegst du auch keine lorentzinvariante Theorie mehr dabei heraus.
| Zitat: |
Nun ist es doch in der Literatur häufig so, dass man gerne die lorentzinvarianz der Maxwell-Gleichungen zeigen möchte und dazu die Maxwellgleichungen in die sogenannte kovariante Form bringt. Man hat dann letztlich zwei Gleichungen. Eine homogene und eine inhomogene Gleichung.
Kovarianz bedeutet doch einfach nur, dass sich beide Seiten bei einem Kartenwechsel gleich transformieren oder? Über lorentzinvarianz sagt das ja noch nichts aus.
|
"Kovarianz" ist, ähnlich wie "Forminvarianz" ein weiterer Begriff, der alles mögliche bedeuten kann. Ich denke oft ist damit einfach gemeint, daß die Objekte in der Gleichung Tensor- oder Spinordarstellungen der Lorentzgruppe bilden. Und, ja, das hat höchstens indirekt etwas mit Lorentzinvarianz zu tun.
| Zitat: |
Ich hab grad mal im Jackson geblättert. Dort steht:
| Zitat: |
Bereits vor der Formulierung der speziellen Relativitätstheorie zeigten Lorentz und Poincaré, dass die Gleichungen der Elektrodynamik unter Lorentztransformationen forminvariant sind. Diese Forminvarianz oder auch Kovarianz , wie sie z.B. die Maxwell-Lorentzsche Gleichung für die Kraft auf ein geladenes Teilchen ...
|
Hier wird zunächst forminvarianz und kovarianz gleichgesetzt, wobei ich dachte dass es nicht dasselbe sei.
|
Ich empfehle dir, dich nicht zu sehr an diesen Begriffen aufzuhängen. Dazu sind sie zu vage. Meine Daumenregel für die Interpretation ist "Forminvarianz" = Invarianz (also ist "Form" redundant, was für diesen Gummibegriff auch nicht weiter tragisch ist.) Und "Kovarianz" = Gleichung zwischen Tensoren oder Spinoren. Beides sind zwar verschiedene Eigenschaften, aber es besteht auch ein Zusammenhang. (siehe Invarianzbedingung (2) weiter oben).
| Zitat: |
In dem ganzen Kapitel werden dann die Maxwell-Gleichungen in die kovariante Form gebracht. Es wird auch von der "Forderung nach lorentzkovarianz" gesprochen. Was soll denn Lorentzkovarianz sein?
|
Weiß ich nicht. Wenn Jackson diesen Begriff verwendet, muß er ihn definieren. (Wenn er dies nicht tut, hält er ihn vielleicht selbst nicht für besonders wichtig.) Wenn ich raten sollte, würde ich sagen: "-kovarianz" = "Tensoren..."; "lorentz-" = "... auf dem Minkowskiraum".
| Zitat: |
| Zitat: | Kleine Abschweifung: Der Punkt, über den du hier gestolpert bist, hat übrigens eine Analogie in der Newtonschen Mechanik. Es scheinen viele die Galileiinvarianz der Theorie für eine triviale Folge aus der "Definition der Kraft"  zu halten. Das Argument geht so: Unter zu halten. Das Argument geht so: Unter  ist offenbar die Beschleunigung invariant ist offenbar die Beschleunigung invariant  . Aber . Aber  per Definition. Also scheint auch F' = F zu folgen. (Wer ein Faible für besonders wasserdichte Argumente hat, schließt dann noch die "Lücke" m'=m mit dem Hinweis, daß die Masse ein "Skalar" ist.) Aber natürlich kann höchstens eine der Gleichungen per Definition. Also scheint auch F' = F zu folgen. (Wer ein Faible für besonders wasserdichte Argumente hat, schließt dann noch die "Lücke" m'=m mit dem Hinweis, daß die Masse ein "Skalar" ist.) Aber natürlich kann höchstens eine der Gleichungen  oder oder  eine "Definition" sein, da F ja normalerweise von x abhängt und diese Abhängigkeit das Transformationsgesetz von F festlegt. eine "Definition" sein, da F ja normalerweise von x abhängt und diese Abhängigkeit das Transformationsgesetz von F festlegt.
|
Kann man denn die Galilei-invarianz zeigen, wenn man die x-Abhängigkeit der Kraft wie folgt einschränkt
)
Das soll eine zweiteilchen_Wechselwirkung repräsentieren. v sind die geschwindigkeiten. Dann müsste ja wegen =F(x_2-x_1, v_2-v_1)) die galilei invarianz offensichtlich sein, wobei die gestrichenen Größen die galileitransformierten Koordinaten sind. die galilei invarianz offensichtlich sein, wobei die gestrichenen Größen die galileitransformierten Koordinaten sind.
|
Ja, genau. Das Paar
)
)
von Bewegungsgleichungen ist trivialerweise invariant unter Galileiboosts und Raumzeit-Translationen. Es ist nicht unbedingt invariant unter Rotationen. Dazu muß zusätzlich gelten
, R(\dot x_1 - \dot x_2)) = RF_i(x_1 - x_2, \dot x_1 - \dot x_2))
| Zitat: |
Wäre dann die galilei invarianz eigentlich verletzt, wenn ich ein externes Kraftfeld nehme.
|
Ja, das einzige externe externe Kraftfeld, das invariant unter der vollen Lorentzgruppe ist, ist F=0. Aus der Forderung nach Boost- und Translationsinvarianz folgt, daß externe Kräfte nicht vom Ort oder Geschwindigkeit des Teilchens oder von t abhängen dürfen, also sind sie konstant. Der einzige Rotationsinvariante Vektor ist aber der Nullvektor.
| Zitat: |
Was ich mir dadurch erkläre, dass so eine Beschreibung unvollständig ist, da eigentlich auch ein externes Feld durch paarweise Wechselwirkungen zustande kommen.
|
Richtig, Kräfte sind immer Wechselwirkungen mit anderen Teilchen. Externe Kräfte sind höchstens Näherungen. |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 05. Nov 2021 16:49 Titel: Kelvin1995 Verfasst am: 05. Nov 2021 16:49 Titel: |
 |
|
Vielen Dank
ich hab jetzt noch zu Herleitungen des Noether-Theorems Folgendes gesehen.
Man hat die Wirkung
 dt)
Und jetzt führt man eine Transformation durch:
)
)
Mit der festlegung, dass alpha ein Parameter ist und für alpha=0 man die untransformierten Koordinaten hat.
Und dann folgt halt ne standardmäßige Herleitung des Theorems.
Was ich mich dabei frage ist Folgendes. Wenn ich die Zeit transformiere, muss doch zwangsläufig auch der Ort transformiert werden, da dieser von der Zeit abhängig ist. In der Herleitung und auch der späteren Verwendung, scheint man aber die Zeit unabhängig vom Ort zu variieren.
Wenn nun die Wirkung invariant unter einer Zeitranslation ist, in dem sinne, dass ich dabei den Ort konstant halte, inwiefern hat dann die zugrundeliegende DGL eine Zeittranslationsinvarianz?
Weil wenn ich ne DGL habe und dort direkt die Symmetrie nachweisen möchte, transformier ich doch die Trajektorie q(t) auf q(t+a) und zeige, dass q(t+a) dieselbe DGL erfüllt wie q(t). aber dann transformier ich ja den Ort oder nicht? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 05. Nov 2021 17:30 Titel: index_razor Verfasst am: 05. Nov 2021 17:30 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | Vielen Dank
ich hab jetzt noch zu Herleitungen des Noether-Theorems Folgendes gesehen.
Man hat die Wirkung
 dt)
Und jetzt führt man eine Transformation durch:
)
)
Mit der festlegung, dass alpha ein Parameter ist und für alpha=0 man die untransformierten Koordinaten hat.
Und dann folgt halt ne standardmäßige Herleitung des Theorems.
Was ich mich dabei frage ist Folgendes. Wenn ich die Zeit transformiere, muss doch zwangsläufig auch der Ort transformiert werden, da dieser von der Zeit abhängig ist.
|
Nein, die einfachste Klasse von Symmetrietransformationen (Punkttransformation) sind Transformation des erweiterten Konfigurationsraums, in diesem Fall also  , d.h. wir betrachten Abbildungen , d.h. wir betrachten Abbildungen
,\ t \mapsto h(q, t, \alpha),)
wovon deine Transformationsgleichung ein Spezialfall ist. f und h sind hier erstmal unabhängige Funktionen. Davon unterscheiden mußt die Transformationen von Funktionen ) , (die zusammen mit ihren Ableitung in der Differentialgleichung auftauchen), die sich aus der Form von f und h zusammen ergeben. , (die zusammen mit ihren Ableitung in der Differentialgleichung auftauchen), die sich aus der Form von f und h zusammen ergeben.
| Zitat: |
In der Herleitung und auch der späteren Verwendung, scheint man aber die Zeit unabhängig vom Ort zu variieren.
|
Ja, Ort x und Zeit t werden unabhängig voneinander variiert. Und dann wird daraus die Transformation von Funktionen ) abgeleitet. abgeleitet.
| Zitat: |
Wenn nun die Wirkung invariant unter einer Zeitranslation ist, in dem sinne, dass ich dabei den Ort konstant halte, inwiefern hat dann die zugrundeliegende DGL eine Zeittranslationsinvarianz?
Weil wenn ich ne DGL habe und dort direkt die Symmetrie nachweisen möchte, transformier ich doch die Trajektorie q(t) auf q(t+a) und zeige, dass q(t+a) dieselbe DGL erfüllt wie q(t). aber dann transformier ich ja den Ort oder nicht? |
Nein, du transformierst eine Funktion der Zeit, nicht den Ort. |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 05. Nov 2021 18:55 Titel: Kelvin1995 Verfasst am: 05. Nov 2021 18:55 Titel: |
 |
|
Also heißt das beim Noether-Theorem betrachtet man zunächst Transformationen im Konfigurationsraum und schaut welche Auswirkungen diese Transformationen auf die Wirkung haben und wenn die Wirkung sich eben nicht ändert, ist es eine Symmetrie?
Wenn ich also jetzt bspw im Konfigurationsraum eine Transformation durchführe, die einer reinen Zeittranslation entspricht, hätte das also direkte Auswirkungen auf die Funktion x(t), da sich das dann nämlich gemäß x(t+a) transformiert?
Inwiefern ergibt sich denn aus einer Lagrangefunktion, bzgl der die Wirkung konstant bei einer Zeittranslation ist, die Invarianz der DGL für die Funktion x(t). Der Zusammenhang ist mir irgendwie noch nicht ganz klar.
Wenn man aus dem Wirkungsfunktional die Euler-Lagrange-Gleichungen ableiten möchte, macht man ja keine Transformation im Konfigurationsraum betrachten, sondern variiert die Funktion x(t) bei festgehaltenem Rand und das ist etwas anderes als eine Transformation im erweiterten Konfigurationsraum oder? Nur zum Verständnis.
Ich glaube, dass ich da zwei Dinge durcheinandergebracht habe. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 05. Nov 2021 20:24 Titel: index_razor Verfasst am: 05. Nov 2021 20:24 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | Also heißt das beim Noether-Theorem betrachtet man zunächst Transformationen im Konfigurationsraum und schaut welche Auswirkungen diese Transformationen auf die Wirkung haben und wenn die Wirkung sich eben nicht ändert, ist es eine Symmetrie?
|
Ja, die Wirkung ist ein Funktional von Funktionen der Zeit. Eine Transformation im erweiterten Konfigurationsraum induziert eine Transformation von Funktionen der Zeit und damit eine Transformation der Wirkung. Wenn diese Transformation die Wirkung invariant läßt oder nur um Randterme ändert, dann ist es eine Symmetrie der Wirkung. Damit ist es gleichzeitig eine Symmetrie der Bewegungsgleichungen (d.h. der Euler-Lagrange-Gleichungen), aber die Umkehrung gilt nicht.
| Zitat: |
Wenn ich also jetzt bspw im Konfigurationsraum eine Transformation durchführe, die einer reinen Zeittranslation entspricht, hätte das also direkte Auswirkungen auf die Funktion x(t), da sich das dann nämlich gemäß x(t+a) transformiert?
|
Eine reine Zeittranslation im erweiterten Konfigurationraum hat die Form

Aus der Funktion ) wird dabei also die Funktion wird dabei also die Funktion )
| Zitat: |
Inwiefern ergibt sich denn aus einer Lagrangefunktion, bzgl der die Wirkung konstant bei einer Zeittranslation ist, die Invarianz der DGL für die Funktion x(t). Der Zusammenhang ist mir irgendwie noch nicht ganz klar.
|
Meinst du worin der Zusammenhang zwischen Symmetrien der Wirkung und Symmetrien von Differentialgleichungen besteht?
Wenn die Wirkung invariant ist, sind die Euler-Lagrange-Gleichungen der transformierten Wirkung dieselben wie für die ursprünglichen Wirkung. Also bildet eine Symmetrie der Wirkung Lösungen der Euler-Lagrange-Gleichung auf Lösungen der Euler-Lagrange-Gleichung ab. Damit ist es auch eine Symmetrie der Bewegungsgleichung.
| Zitat: |
Wenn man aus dem Wirkungsfunktional die Euler-Lagrange-Gleichungen ableiten möchte, macht man ja keine Transformation im Konfigurationsraum betrachten, sondern variiert die Funktion x(t) bei festgehaltenem Rand und das ist etwas anderes als eine Transformation im erweiterten Konfigurationsraum oder? Nur zum Verständnis.
|
Ja, das ist etwas anderes. Auf diesen Unterschied wollte ich ja schon beim letzten Mal hinaus. Nochmal, die allgemeinste (kontinuierliche) Punkttransformation hat die Form
,\ t' = h(q, t, \alpha))
Unter bestimmten Bedingungen läßt sich daraus einer Transformation von Funktionen der Zeit mit Werten im Konfigurationsraum machen. Die Grundidee ist einfach, daß man jedem Punkt des Graphen (t, x(t)) der Punkttransformation unterzieht, d.h.
) \mapsto [h(x(t), t, \alpha), f(x(t), t, \alpha)])
Das funktioniert natürlich nur, wenn dabei wieder der Graph einer Funktion rauskommt, also , t, \alpha)) lokal nach t aufgelöst werden kann, m.a.W. eine Funktion g existiert, so daß lokal nach t aufgelöst werden kann, m.a.W. eine Funktion g existiert, so daß
, g(t', \alpha), \alpha) = t')
und folglich
, t, \alpha), f(x(t), t, \alpha)]=[t', f(x(g(t',\alpha)), g(t', \alpha))])
In diesem Sinne ist also die Funktion ) nach nach ), g(t', \alpha))) transformiert. transformiert.
Für die Zeittranslation \mapsto (t+\alpha, x)) gilt natürlich gilt natürlich ) \mapsto (t+\alpha, x(t))) und man kann und man kann  = t' -\alpha) wählen mit dem Ergebnis wählen mit dem Ergebnis )) . . |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 06. Nov 2021 12:55 Titel: Kelvin1995 Verfasst am: 06. Nov 2021 12:55 Titel: |
 |
|
Hmm betrachten wir mal als Beispiel die Lagrangefunktion

zu ihr gehört die Bewegungsgleichung

Wie wir wissen, sollte dieses System zeittranslationsinvariant sein.
Als erstes untersuche ich das anhand der DGL
Es gilt für die Transformation der Funktion x(t) unter einer Zeitranslation )
Nun betrachte ich Folgendes
}{dt^\prime}=\frac{d(\frac{dx^\prime}{dt})}{dt^\prime}=\frac{d(\frac{dx^\prime}{dt})}{dt} \frac{dt}{dt^\prime}=\frac{d^2x^\prime}{dt^{2}}=\frac{d^2x(t-\alpha)}{dt^{2}}=0)
Nun möchte ich das mit der Invarianz der Wirkung untersuchen

Die transformierte Wirkung ist:

Ist das hier richtig oder muss man doch das  mittransformieren? mittransformieren?
Weiterhin gilt

Und damit ist die Invarianz gezeigt oder wie? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 07. Nov 2021 07:47 Titel: index_razor Verfasst am: 07. Nov 2021 07:47 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: |
Nun möchte ich das mit der Invarianz der Wirkung untersuchen

Die transformierte Wirkung ist:

Ist das hier richtig oder muss man doch das  mittransformieren? mittransformieren?
|
Du mußt die Geschwindigkeit 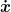 , die Integrationsvariable und die Integrationsgrenzen transformieren. , die Integrationsvariable und die Integrationsgrenzen transformieren.
^2(t')\dd t' = \frac{1}{2}\int_{t_1 + \alpha}^{t_2+\alpha}\dot x^2(t' - \alpha)\dd t' =\frac{1}{2} \int_{t_1}^{t_2}\dot x^2(t)\dd t \equiv S[x])
Im ersten Schritt wurde die transformierte Geschwindigkeit und die transformierten Grenzen eingesetzt, im zweiten Schritt wurde eine Variablensubstitution vorgenommen. |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 07. Nov 2021 15:34 Titel: Kelvin1995 Verfasst am: 07. Nov 2021 15:34 Titel: |
 |
|
Danke
Ich hätte dann noch die Frage ob es beim Noether Theorem egal ist, ob man passive oder aktive Transformationen verwendet. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 07. Nov 2021 15:46 Titel: index_razor Verfasst am: 07. Nov 2021 15:46 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | Danke
Ich hätte dann noch die Frage ob es beim Noether Theorem egal ist, ob man passive oder aktive Transformationen verwendet. |
Über den Zusammenhang zwischen aktiven und passiven Transformationen sowie ihren Bezug zum Noether-Theorem habe weiter oben schon etwas ausführlicher geschrieben. Ist daran etwas unklar geblieben?
Ich persönlich fasse Symmetrietransformationen als aktive Transformationen auf. Darüberhinaus hängt es natürlich von der präzisen Formulierung des Theorems ab, mit welcher Art von Transformation man es zu tun hat. Hast du eine konkrete Formulierung im Sinn? |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 07. Nov 2021 16:01 Titel: Kelvin1995 Verfasst am: 07. Nov 2021 16:01 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Ich persönlich fasse Symmetrietransformationen als aktive Transformationen auf. Darüberhinaus hängt es natürlich von der präzisen Formulierung des Theorems ab, mit welcher Art von Transformation man es zu tun hat. Hast du eine konkrete Formulierung im Sinn? |
Als wir zu Anfang über lorentzinvarianz gesprochen haben, haben wir Kartenwechsel betrachtet und Kartenwechsel sind ja passive Transformationen.
Da geht es ja auch darum, dass man das Koordinatensystem wechselt und man spricht da ja auch von Symmetrien, obwohl das alles passiv war.
Ich stell mir das so vor, dass man auf der einen Seite in unterschiedlichen Karten unterschiedliche Koordinatenfunktionen für dieselbe Bahnkurve hat, die aber jeweils dieselbe DGL lösen. Auf der anderen Seite kann man aber auch eine Koordinatenfunktion in derselben Karte transformieren und erhält eine neue Funktion, die ebenso die DGL löst.
Handelt es sich nicht in beiden Fällen um Symmetrien? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 07. Nov 2021 16:33 Titel: index_razor Verfasst am: 07. Nov 2021 16:33 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Ich persönlich fasse Symmetrietransformationen als aktive Transformationen auf. Darüberhinaus hängt es natürlich von der präzisen Formulierung des Theorems ab, mit welcher Art von Transformation man es zu tun hat. Hast du eine konkrete Formulierung im Sinn? |
Als wir zu Anfang über lorentzinvarianz gesprochen haben, haben wir Kartenwechsel betrachtet und Kartenwechsel sind ja passive Transformationen.
Da geht es ja auch darum, dass man das Koordinatensystem wechselt und man spricht da ja auch von Symmetrien, obwohl das alles passiv war.
|
Was heißt "man spricht von Symmetrien"? Um welche Aussage genau geht es? Meine Intention von Anfang an war eigentlich klar zu machen, daß Lorentzinvarianz nichts mit Koordinatenwechseln zu tun hat. Oder wie ich damals schrieb:
| index_razor hat Folgendes geschrieben: | | Die besondere Rolle der Lorentztransformation kommt aus dem Relativitätsprinzip, also der Aussage, daß die Lorentzgruppe (oder allgemeiner Poincaregruppe) eine Symmetrie der dynamischen Grundgleichungen ist. Das hat mit Kartenwechseln eigentlich gar nichts zu tun. |
Abgesehen von der relativ unwichtigen Tatsache, daß man mit zwei Karten  im Prinzip auch eine aktive Transformation im Prinzip auch eine aktive Transformation  und damit evtl. eine Symmetrietransformation definieren kann, gibt es dem aus meiner Sicht eigentlich nichts hinzuzufügen. und damit evtl. eine Symmetrietransformation definieren kann, gibt es dem aus meiner Sicht eigentlich nichts hinzuzufügen.
| Zitat: |
Ich stell mir das so vor, dass man auf der einen Seite in unterschiedlichen Karten unterschiedliche Koordinatenfunktionen für dieselbe Bahnkurve hat, die aber jeweils dieselbe DGL lösen.
|
Die Differentialgleichung bezieht sich auf die Bahnkurve, nicht auf ihre Koordinatenfunktionen. Möglicherweise ist dir nicht klar, wie man Differentialgleichungen und ihre Lösungsmengen koordinatenunabhängig definiert. Weiter oben habe ich das bereits angedeutet. Eine Differentialgleichung n-ter Ordnung definiert eine Untermannigfaltigkeit in einem n-Jet-Raum. Das ist ein geometrisches, koordinatenunabhängiges Objekt. Darauf kannst du, wie auf jeder Mannigfaltigkeit, natürlich Karten definieren. Aber die ändern nichts an der Definition der Differentialgleichung oder den Eigenschaften ihrer Lösungsmenge.
| Zitat: |
Auf der anderen Seite kann man aber auch eine Koordinatenfunktion in derselben Karte transformieren und erhält eine neue Funktion, die ebenso die DGL löst.
Handelt es sich nicht in beiden Fällen um Symmetrien? |
Wie du selbst geschrieben hast, ändert eine Koordinatentransformation die Bahnkurve nicht. Damit handelt es sich also um dieselbe Lösung wie vorher und damit im besten Fall um eine triviale Symmetrietransformation. Eine nichttriviale Symmetrie erfordert eine Änderung der Bahnkurve derart, daß die geänderte Bahnkurve eben wieder eine Lösung ist. Das ist aber nur ein Umformulierung deiner eigenen Definition von Symmetrietransformation. Irgendwas scheint also an dieser Definition noch unklar zu sein. |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 07. Nov 2021 16:49 Titel: Kelvin1995 Verfasst am: 07. Nov 2021 16:49 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Als wir zu Anfang über lorentzinvarianz gesprochen haben, haben wir Kartenwechsel betrachtet und Kartenwechsel sind ja passive Transformationen.
Da geht es ja auch darum, dass man das Koordinatensystem wechselt und man spricht da ja auch von Symmetrien, obwohl das alles passiv war.
|
Wenn man sich Einführungen in die SRT anschaut, dann betrachtet man doch immer Wechsel des Inertialsystems und solche Wechsel sind doch letztlich spezielle Kartenwechsel.
Also betrachtet man bei der lorentzinvarianz von DGLs keine Wechsel von Inertialsystemen, sondern unterzieht den Bahnkurven selbst den Lorentz-Boost?
Bei mir implizieren Darstellungen wie
)
dass man die Koordinaten von q nach q' wechselt und nicht, dass man die Stelle q auf die Stelle q' abbildet. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 07. Nov 2021 17:03 Titel: index_razor Verfasst am: 07. Nov 2021 17:03 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | | Kelvin1995 hat Folgendes geschrieben: |
Als wir zu Anfang über lorentzinvarianz gesprochen haben, haben wir Kartenwechsel betrachtet und Kartenwechsel sind ja passive Transformationen.
Da geht es ja auch darum, dass man das Koordinatensystem wechselt und man spricht da ja auch von Symmetrien, obwohl das alles passiv war.
|
Wenn man sich Einführungen in die SRT anschaut, dann betrachtet man doch immer Wechsel des Inertialsystems und solche Wechsel sind doch letztlich spezielle Kartenwechsel.
|
Nein, nicht immer. Lorentztransformationen werden oft als aktive Transformationen  auf dem Minkowskiraum eingeführt, die die Metrik invariant lassen, in dem Sinne, daß auf dem Minkowskiraum eingeführt, die die Metrik invariant lassen, in dem Sinne, daß
 = g(x,y)\qquad \text{(LT)})
| Zitat: |
Also betrachtet man bei der lorentzinvarianz von DGLs keine Wechsel von Inertialsystemen, sondern unterzieht den Bahnkurven selbst den Lorentz-Boost? |
Ja, das sage ich doch die ganze Zeit. "Lorentzinvarianz" bedeutet "Symmetrie unter Lorentztransformationen (LT)". Und du selbst hast Symmetrien als spezielle Transformationen der Bahnkurven definiert.
| Zitat: |
Bei mir implizieren Darstellungen wie
)
dass man die Koordinaten von q nach q' wechselt und nicht, dass man die Stelle q auf die Stelle q' abbildet. |
Das ist eigenartig. Wie sähe denn für dich eine Abbildung der Stelle q auf die Stelle q' aus?
Ich habe zumindest oben diese Abbildung ausdrücklich als Transformation auf dem erweiterten Konfigurationsraum eingeführt. Da war nirgendwo von einer Koordinatentransformation die Rede. |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 07. Nov 2021 17:43 Titel: Kelvin1995 Verfasst am: 07. Nov 2021 17:43 Titel: |
 |
|
Ich glaube das Problem ist, dass mein Gehirn aufgrund meiner Vorbildung einen gewissen Bias hat und es etwas Mühe kostet diesen Bias abzulegen. Deshalb kommt sowas zustande, wie dass mir irgendwie bewusst ist, dass es um aktive Transformationen geht, ich dann aber wieder auf passive Transformationen zurückfalle, weil wenn ich an einführende Veranstaltungen zur SRT denke, dann sehe ich, dass man den Beobachter in andere Inertialsysteme transformiert, nicht aber dass man das beobachtete Objekt transformiert. Man betrachtet zum Beispiel den schiefen Wurf eines Balles mal in einem System bei dem der Ball sich in horizontaler Richtung mit der Geschwindigkeit v bewegt und mal wo er sich mit Geschwindigkeit 0 in horizontaler Richtung bewegt. Solche Sachen sind das halt, weshalb ich gedanklich darauf immer wieder zurückfalle und mir ist es neu dass man die Lorentztransformation als aktive Transformation betrachtet.
Ich mein es ergibt für mich schon Sinn, aber im Rahmen meiner Vorbildung habe ich das anders kennengelernt.
Dazu hätte ich dann doch noch eine Frage.
In einem Buch über klassische Mechanik lese ich Folgendes:
| Zitat: | | Es gibt überabzählbar unendlich viele Inertialsysteme, die über eine Galilei-Transformation miteinander verknüpft sind. Die physikalischen Gesetze sind unter allen Wechsel zwischen den Inertialsystemen forminvariant |
Den Begriff forminvariant betrachte ich mal, wie wir bereits diskutiert haben, einfach als invariant.
Hier geht es doch explizit um den Wechsel zwischen den Inertialsystemen, also um Kartenwechsel und nicht um aktive Transformationen oder?
Das steht dann aber im Widerspruch dazu, dass man die Invarianz bzgl aktiver Transformationen untersucht. Wenn es darum geht, dass Gesetze unabhängig vom Beobachter sein sollen, geht es doch um passive Transformation oder nicht?
| Zitat: | | Das ist eigenartig. Wie sähe denn für dich eine Abbildung der Stelle q auf die Stelle q' aus? |
Die Frage ist, wie und ob man durch eine Notation unterscheiden kann, ob es sich um eine aktive oder eine Koordinaten-Transformation handelt. Wenn das geht, wäre es für mich hilfreich. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18080
|
 TomS Verfasst am: 08. Nov 2021 07:36 Titel: TomS Verfasst am: 08. Nov 2021 07:36 Titel: |
 |
|
Anhand der Transformationsvorschrift alleine kann man das nicht unterscheiden, es ist eine Frage der Interpretation.
Einfaches Beispiel: Schau dir mal die Transformation

an. Du kannst nicht unterscheiden, ob
i) y immer den selben Ort mit neuen Koordinaten (y,t) bzgl. eines anderen Bezugssystems vermöge der Galilei-Transformation (= eines Boosts mit Geschwindigkeit v) bezeichnet, oder ob
ii) y stattdessen eine Schar unterschiedlicher Orte
 = x - vt)
entlang einer Trajektorie eines Teilchens bezeichnet.
Die Formel alleine liefert dir diese Unterscheidung nicht, es kommt auf die physikalische Motivation bzw. den Kontext an.
Speziell zur Frage der Diffeomorphismen findest du evtl. folgende Diskussion hilfreich:
https://www.physikerboard.de/htopic,63514,diffeomorphismus.html
Auch hier liefert die Transformationsvorschrift der Koordinaten nicht die Bedeutung des Diffeomorphismus - aktiv oder passiv (= Abbildung zwischen Karten).
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 08. Nov 2021 08:44, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 08. Nov 2021 08:17 Titel: index_razor Verfasst am: 08. Nov 2021 08:17 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: | | Ich glaube das Problem ist, dass mein Gehirn aufgrund meiner Vorbildung einen gewissen Bias hat und es etwas Mühe kostet diesen Bias abzulegen. Deshalb kommt sowas zustande, wie dass mir irgendwie bewusst ist, dass es um aktive Transformationen geht, ich dann aber wieder auf passive Transformationen zurückfalle, weil wenn ich an einführende Veranstaltungen zur SRT denke, dann sehe ich, dass man den Beobachter in andere Inertialsysteme transformiert, nicht aber dass man das beobachtete Objekt transformiert. |
Man kann beides tun. Das einzige Problem ist nur, daß man in der Koordinatensprache der Physiker beides nicht klar auseinanderhalten kann. Deswegen muß man alles im Kontext lesen.
| Zitat: |
Dazu hätte ich dann doch noch eine Frage.
In einem Buch über klassische Mechanik lese ich Folgendes:
| Zitat: | | Es gibt überabzählbar unendlich viele Inertialsysteme, die über eine Galilei-Transformation miteinander verknüpft sind. Die physikalischen Gesetze sind unter allen Wechsel zwischen den Inertialsystemen forminvariant |
Den Begriff forminvariant betrachte ich mal, wie wir bereits diskutiert haben, einfach als invariant.
Hier geht es doch explizit um den Wechsel zwischen den Inertialsystemen, also um Kartenwechsel und nicht um aktive Transformationen oder?
Das steht dann aber im Widerspruch dazu, dass man die Invarianz bzgl aktiver Transformationen untersucht.
|
Ein Inertialsystem definiert eine globale Karte 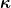 auf der Raumzeit. Eine Galileitransformation auf der Raumzeit. Eine Galileitransformation  bildet Ereignisse auf Ereignisse ab. Also bildet jede Gailieitransformation ein Inertialsystem auf eine andere globale Karte ab, nämlich bildet Ereignisse auf Ereignisse ab. Also bildet jede Gailieitransformation ein Inertialsystem auf eine andere globale Karte ab, nämlich  . Dieses . Dieses  ist wieder ein Inertialsystem. Umgekehrt definiert jeder Wechsel ist wieder ein Inertialsystem. Umgekehrt definiert jeder Wechsel  von Inertialsystemen eine aktive Galileitransformation von Inertialsystemen eine aktive Galileitransformation  . Das ist der Inhalt der ersten Aussage. . Das ist der Inhalt der ersten Aussage.
Eine Gleichung  ist invariant unter Galileitransformationen wenn ist invariant unter Galileitransformationen wenn  . (Die Forderung ist etwas zu streng, aber es geht mir nur ums Prinzip.) Die linke Seite bedeutet: "Unterziehe alle Größen in G einer Galileitransformation." Die "Form" dieser Gleichung bzgl. der Koordinaten . (Die Forderung ist etwas zu streng, aber es geht mir nur ums Prinzip.) Die linke Seite bedeutet: "Unterziehe alle Größen in G einer Galileitransformation." Die "Form" dieser Gleichung bzgl. der Koordinaten 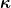 ist meinetwegen ist meinetwegen  . Hier bedeutet die linke Seite soviel wie "Setze alle Komponenten der Größen in G ein und baue sie zu Vektoren, Tensoren etc. zusammen". Für . Hier bedeutet die linke Seite soviel wie "Setze alle Komponenten der Größen in G ein und baue sie zu Vektoren, Tensoren etc. zusammen". Für  , wäre dann z.B. , wäre dann z.B.  etc. etc.
Dann gilt also  . Also ist die "Form" von G bzgl der einen Karte gleich der "Form" bzgl. der anderen Karte. Allerdings gilt das auch wenn . Also ist die "Form" von G bzgl der einen Karte gleich der "Form" bzgl. der anderen Karte. Allerdings gilt das auch wenn 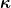 kein Inertialsystem ist. Hauptsache kein Inertialsystem ist. Hauptsache  ist eine Galileitransformation. Die "Form" wäre dann vielleicht eine andere, aber invariant unter ist eine Galileitransformation. Die "Form" wäre dann vielleicht eine andere, aber invariant unter  wäre sie trotzdem. Die ganzen Gleichungen sind hier natürlich eher symbolisch zu lesen. Ich beabsichtige keine präzise Definition der "Form" einer Gleichung oder deren Invarianz. wäre sie trotzdem. Die ganzen Gleichungen sind hier natürlich eher symbolisch zu lesen. Ich beabsichtige keine präzise Definition der "Form" einer Gleichung oder deren Invarianz.
| Zitat: |
Wenn es darum geht, dass Gesetze unabhängig vom Beobachter sein sollen, geht es doch um passive Transformation oder nicht?
|
Ich weiß nicht, worum es in dem Buch geht. Wie ich bereits sagte, muß man solche Aussagen oft im Kontext lesen.
| Zitat: |
| Zitat: | | Das ist eigenartig. Wie sähe denn für dich eine Abbildung der Stelle q auf die Stelle q' aus? |
Die Frage ist, wie und ob man durch eine Notation unterscheiden kann, ob es sich um eine aktive oder eine Koordinaten-Transformation handelt. Wenn das geht, wäre es für mich hilfreich. |
Warum wilst du das durch die Notation unterscheiden? Zu einer Abbildung gehört die Angabe eines Definitions- und eines Wertebereichs. Wenn beides Teilmengen der Mannigfaltigkeit M sind, ist es eine aktive Transformation. Wenn eine Teilmenge von M auf  abgebildet wird, ist es eine Karte. abgebildet wird, ist es eine Karte. |
|
 |
Kelvin1995
Gast
|
 Kelvin1995 Verfasst am: 09. Nov 2021 21:29 Titel: Kelvin1995 Verfasst am: 09. Nov 2021 21:29 Titel: |
 |
|
Ich danke euch beiden.
Ich habe dazu noch ein paar Übungsaufgaben gerechnet, um damit vertrauter zu werden und ich glaube so langsam, verstehe ich es.
Mein Ziel ist es letztlich die Quantenfeldtheorien und die allgemeine Relativitätstheorie zu verstehen. Der nächste Baustein, der auch noch etwas mit diesem Topic zu tun hat, wäre zu verstehen, was ein Spinorfeld ist.
Meine Vorstellungen von Spinoren sind momentan noch sehr vage, aber ich wollte mal fragen, ob meine vagen Vorstellungen überhaupt richtig sind.
Soweit ich das verstehe sind Spinoren zunächst auch Vektoren, da sie Elemente des Darstellungsraums einer Darstellung der Spingruppe sind.
Nun weiß ich aber auch, dass sich Spinorfelder von Tensorfelder dadurch unterscheiden, dass sie sich anders transformieren, wenn man auf der Mannigfaltigkeit eine aktive Transformation durchführt. Die Elemente eines Vektorfeldes, transformieren sich ja nach dem pushforward.
Ich habe mich jetzt gefragt was denn der Unterschied zwischen einem Spinorfeld und einem Vektorfeld sein kann, da Spinoren ja auch Vektoren sind.
Meine Vermutung wäre, dass es daran liegt, dass man beim Vektorfeld Vektoren aus den Tangentialräumen nimmt und die Spinoren des Spinorfeldes sind keine Elemente aus den Tangentialräumen, sondern eines anderen Raumes. Wie der andere Vektorraum aussieht und wie man daraus das andere Transformationsverhalten bestimmt, weiß ich noch nicht. Also sind Spinorfelder keine Tensorfelder, aber sowohl Spinoren als auch Tensoren sind Vektoren. Kommt das hin?
Kommt man in der Physik meistens damit aus, wenn man sich Dirac-Spinoren als "Vierer-Vektoren" vorstellt, nur dass man dann halt bei der Transformation aufpassen muss und sie nicht wie sonstige Vierer-Vektoren transformieren darf?
Vielen Dank |
|
 |
jh8979
Moderator

Anmeldungsdatum: 10.07.2012
Beiträge: 8583
|
 jh8979 Verfasst am: 09. Nov 2021 21:54 Titel: jh8979 Verfasst am: 09. Nov 2021 21:54 Titel: |
 |
|
| Kelvin1995 hat Folgendes geschrieben: |
Kommt man in der Physik meistens damit aus, wenn man sich Dirac-Spinoren als "Vierer-Vektoren" vorstellt, nur dass man dann halt bei der Transformation aufpassen muss und sie nicht wie sonstige Vierer-Vektoren transformieren darf?
|
Solange man nur QED macht ja. Danach lohnt es sich Weyl-Spinoren zu verstehen.
Aber ich würde vorschlagen: Schritt für Schritt. Die Quantenfeldtheorie aus Sicht eines Mathematikers verstehen zu wollen, halte ich im ersten Anlauf für wenig erfolgversprechend. Erst wie ein Physiker: quick and dirty, dann langsam die schmutzigen Ecken auffüllen, so gut es geht...  |
|
 |
|
|

















