| Autor |
Nachricht |
Colophonius Regenschein
Gast
|
 Colophonius Regenschein Verfasst am: 05. Sep 2021 13:26 Titel: Ladungsverteilung eines Körpers berechnen Colophonius Regenschein Verfasst am: 05. Sep 2021 13:26 Titel: Ladungsverteilung eines Körpers berechnen |
 |
|
Meine Frage:
Hallo zusammen,
ich möchte in einer Computersimulation die Ladungsverteilung bestimmen in einem leitenden Körper aus Voxeln mit einer gegebenen externen Spannung
Beispiel einer Anordnung von Voxeln:

Jeder Voxel hat eine Ladung  die ich bestimmen will für den elektrostatischen Fall. die ich bestimmen will für den elektrostatischen Fall.
Mein Ansatz:
Prämisse 1:in jedem Voxel muss das Potential gleich sein, da sonst Ladung sich durch ein resultierendes E-Feld bewegen und umverteilen würde. Das Potential in jedem Punkt entspricht der externen Spannungsquelle.
Das Potential rechne ich in jedem Punkt i aus mit dem Coulombpotential ausgehend von allen anderen Ladungen: (Konstanten sind alle auf 1 gesetzt)
 , mit , mit  da ein Ladungspunkt keine Kraft auf sich selbst ausübt in der Elektrostatik. da ein Ladungspunkt keine Kraft auf sich selbst ausübt in der Elektrostatik.  besschreibt Abstand zwischen i und j. besschreibt Abstand zwischen i und j.
Mit Prämisse 1 setze ich alle  gleich und löse das Gleichungssystem und kriege so alle gleich und löse das Gleichungssystem und kriege so alle  und somit die Ladungsverteilung die ich bestimmen wollte. und somit die Ladungsverteilung die ich bestimmen wollte.
Mein Problem:
Das Ergebnis ist kontraintuitiv. Meine Berechnungen ergeben, dass Ladungen sich bevorzugt in der Mitte von Körpern aufhalten.
gleichnamige Ladungen müssten ja durch Abstoßung sich möglichst weit von einander entfernt aufhalten wollen.
Beispiel:
Seien 3 Voxel nebeneinander  mit mit  und und  und externer Spannung von 10 erhalten wir die Gleichungen und externer Spannung von 10 erhalten wir die Gleichungen

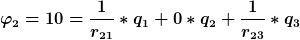

Wir erhalten das Gleichungssystem

löse ich durch das Gaußsche Eliminationsverfahren.

Warum ist die Ladungsdichte außen in Punkt 1 und 3 nicht am Höchsten sondern in der Mitte in Punkt 2?
Nun können sich ja auch gar nicht Ladungen im inneren von leitern aufhalten, sonder nur am Rand.
Im 3-dimensionalen Fall hätte der Punkt 2 aber noch 4 äußere Randflächen ohne Nachbarn. Wäre Punkt 2 also innen oder außen? Was wäre mit den Punkten 3 und 7 in obiger Anordnung, innen oder außen?
Würde die Bedingung, dass im Inneren keine Ladungen sein dürfen aus den Gleichungen folgen müssen oder muss ich das als externe Zwangsbedingung einführen?
Meine Ideen:
Ich nehme an, dass entweder Prämisse 1 falsch ist oder ich einen Rechenfehler habe.
Ich fürchte ich habe in der Elektrostatik noch ein paar Missverständnisse. Hoffe auf Denkansätze  . .
|
|
 |
gast002
Gast
|
 gast002 Verfasst am: 07. Sep 2021 11:21 Titel: gast002 Verfasst am: 07. Sep 2021 11:21 Titel: |
 |
|
Sehr geehrter Herr Colophonius Regenschein,
das von Ihnen aufgestellte Problem erscheint mir interessant. Leider bin ich kein Theoretiker und kann es nicht lösen. Da aber bisher sonst niemand geantwortet hat, will ich die Überlegungen mitteilen, die ich mir gemacht habe.
1. Der Ansatz, bei der Summe der Potentiale der Einzelladungen j zur Ermittlung des Potentials am Ort i die Ladung i wegzulassen, könnte problematisch sein. Ja, formal mathematisch ist es notwendig, um den Ausdruck 1/0 zu vermeiden, aber physikalisch wird dadurch das System der Ladungen verändert.
Das tatsächliche Potential in dem Gebiet des Ladungssystems kann man berechnen, indem man eine kleine Probeladung verwendet, zusätzlich zu den vorgegebenen Ladungen q_i. Die Probeladung q_p muß viel kleiner sein, als die Ladungen q_i, damit das Potential durch sie nicht verändert wird. Damit darf dann auch in der Summe zur Berechnung des Potentials die Ladung q_p entfallen, aber die ursprünglichen Ladungen q_i sind jetzt alle enthalten.
Sieht man sich mit dieser Betrachtungsweise das Potential im 3-Ladungssystem des Beispiels an, so hat man um jede Ladung einen Coulombtrichter, eine Singularität. Das heißt aber, direkt am Ort der Ladungen q_i ist das Potential nicht definiert. Folglich kann die Bedingung, es soll an allen Orten i gleich sein, auch nicht aufgestellt werden.
Betrachtet man das Potential in einem kleinen Abstand Epsilon von den Orten i, ist es bei der mittleren Ladung größer, als bei den beiden am Rand.
2. Ein weiteres Problem könnte sein, daß Sie mit einem System weniger diskreter Ladungen rechnen, aber bei der Interpretation des Resultats mit dem Verhalten sehr vieler Ladungen in einem metallischen Leiter argumentieren. Wenn ihre Möglichkeiten für numerische Rechnungen es zulassen, wäre es interessant zu testen, wie sich die Verteilung der Ladungen verhält, wenn deren Anzahl deutlich größer wird, 10, 50, 200, 1000.
3. Das Beispiel ist nur für eine eindimensionale Anordnung der Ladungen gerechnet. Es ist bekannt, daß sich ein-, zwei- und dreidimensionale Probleme sehr unterschiedlich verhalten können. Also sollte auch das in Modellrechnungen getestet werden.
In der Hoffnung, daß meine Überlegungen hilfreich seien verbleibe ich mit
Besten Grüßen
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 07. Sep 2021 13:03 Titel: TomS Verfasst am: 07. Sep 2021 13:03 Titel: |
 |
|
@ Colophonius-Regenschein:
Man kann die einzelnen Ladungen natürlich festhalten, aber ich denke nicht, dass das gemeint ist.
Ich gehe aus von
)
Der erste Term beschreibt die Coulomb-Energie aller Ladungspaare i,j, wobei jedes Paar nur einmal gezählt wird und wobei i ungleich k ist. Der zweite Term beschriebt die Energie der Ladungen im äußeren Feld Phi am Ort der i-ten Ladung.
Für ein homogene Feld in z-Richtung mit Feldstärke E_0 kann man natürlich
 = E_0 z)
setzen.
Die Gleichgewichtspunkte für die Ladungen folgen aus der Lösung des Gleichungssystems

wobei zusätzlich noch die zweiten Ableitungen zu betrachten sind, um zwischen Minima, Maxima und Sattelpunkten unterscheiden zu können.
Das exakt beweisbare Earnshaw-Theorem besagt, dass kein Potential und damit keine Ladungskonfiguration existiert, für die ein stabiles Gleichgewicht vorliegt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
 DrStupid Verfasst am: 07. Sep 2021 15:10 Titel: DrStupid Verfasst am: 07. Sep 2021 15:10 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Man kann die einzelnen Ladungen natürlich festhalten, aber ich denke nicht, dass das gemeint ist. |
Wenn man sie nicht festhält, dann fliegt alles auseinander. Irgendeine Zwangsbedingung braucht man. In diesem Fall besteht sie darin, dass sich die Ladungen nur in den Zentren der Voxel aufhalten dürfen.
| TomS hat Folgendes geschrieben: | Die Gleichgewichtspunkte für die Ladungen folgen aus der Lösung des Gleichungssystems
 |
Wenn die freien Parameter nur die Ladungen der Voxel sind, dann führt das zu der Gleichung mit der auch Colophonius-Regenschein rechnet.
Ein Problem liegt möglicherweise in der räumlichen Diskretisierung. Es wird ja angenommen, dass die Ladung eines Voxels in einem Punkt konzentriert ist. Tatsächlich resultiert sie aber aus vielen Ladungsträgern, die möglichst weit voneinander weg wollen. Die Auflösung immer weiter zu erhöhen, bis man pro Gitterpunkt nur noch zwischen Ladungsträger oder kein Ladungsträger unterscheiden kann, scheint mir aber auch keine praktikable Lösung zu sein.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 07. Sep 2021 15:26 Titel: TomS Verfasst am: 07. Sep 2021 15:26 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | Wenn man sie nicht festhält, dann fliegt alles auseinander.
|
Wenn man entweder ausschließlich positive Ladungen oder ausschließlich negative Ladungen zulässt, dann ja.
| DrStupid hat Folgendes geschrieben: | | Wenn die freien Parameter nur die Ladungen der Voxel sind, dann führt das zu der Gleichung mit der auch Colophonius-Regenschein rechnet. |
Sicher?
Evtl. habe ich die Problemstellung noch nicht genau genug verstanden.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
 DrStupid Verfasst am: 07. Sep 2021 16:29 Titel: DrStupid Verfasst am: 07. Sep 2021 16:29 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Wenn man entweder ausschließlich positive Ladungen oder ausschließlich negative Ladungen zulässt, dann ja. |
Wenn verschiedene Bereiche desselben elektrisch leitenden Körpers entgegengesetzte Ladungen hätten, dann ergäbe das einen Kurzschluss. Das wäre so ziemlich das Gegenteil von dem Gleichgewicht, nach dem hier gesucht wird.
| TomS hat Folgendes geschrieben: | | Sicher? |
Zumindest so, wie ich das Problem interpretiere.
Am Körper liegt überall die gleiche Spannung an. Das heißt
 = E_0)
Damit gilt

Das würde sich ändern, wenn man annimmt, dass die Ladung in jedem Voxel gleichmäßig verteilt ist. Das ist zwar auch nicht korrekt, aber besser als eine Konzentration der Ladung im Zentrum. Die Berechnung wird dann natürlich viel komplizierter.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 07. Sep 2021 16:55 Titel: TomS Verfasst am: 07. Sep 2021 16:55 Titel: |
 |
|
| DrStupid hat Folgendes geschrieben: | | Wenn verschiedene Bereiche desselben elektrisch leitenden Körpers entgegengesetzte Ladungen hätten, dann ergäbe das einen Kurzschluss. Das wäre so ziemlich das Gegenteil von dem Gleichgewicht, nach dem hier gesucht wird. |
Das hjatte ich doch tatsächlich überlesen.
| TomS hat Folgendes geschrieben: | Am Körper liegt überall die gleiche Spannung an. Das heißt
 = E_0)
Damit gilt
 |
Verstehe ich nicht.
Zum ersten ist das elektrische Feld konstant, nicht jedoch das Potential.
Und zum zweiten spreche ich von der Lösung eines Extremalproblems und daher einem Gradienten im Ortsraum, während du nach der Ladung ableitest.
Aber evtl. verstehe ich die Problemstellung zu wenig.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
 DrStupid Verfasst am: 08. Sep 2021 08:45 Titel: DrStupid Verfasst am: 08. Sep 2021 08:45 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | | Zum ersten ist das elektrische Feld konstant, nicht jedoch das Potential. |
Soweit ich es verstehe ist das Potential konstant und das elektrische Feld konstant Null.
| TomS hat Folgendes geschrieben: | | Und zum zweiten spreche ich von der Lösung eines Extremalproblems und daher einem Gradienten im Ortsraum, während du nach der Ladung ableitest. |
Mir ist klar, dass Du von der Lösung eines Extremalproblems sprichst. Du suchst die Extrema von U. Allerdings hängt U nicht von den Orten der Voxel ab (die sind festgelegt) sondern von ihren Ladungen.
| TomS hat Folgendes geschrieben: | | Aber evtl. verstehe ich die Problemstellung zu wenig. |
Am ehesten könnte man das Ganze als ein Gitter von identischen Kugelkondensatoren modellieren, deren innere Pole auf Masse liegen und deren äußere Pole mit denen der Nachbarn verbunden sind. Diese Konstruktion wird elektrisch aufgeladen. Die Frage ist, wie sich die gesamte Ladung auf die einzelnen Kondensatoren verteilt.
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 08. Sep 2021 08:59 Titel: TomS Verfasst am: 08. Sep 2021 08:59 Titel: |
 |
|
Der Fragesteller hat aber auch die Orte und die Ladungsverteilung genannt. Anyway, ohne ihn und besseres Verständnis der Problemstellung kommen wir wohl nicht weiter.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Colophonius Regenschein
Anmeldungsdatum: 09.09.2021
Beiträge: 1
|
 Colophonius Regenschein Verfasst am: 09. Sep 2021 22:06 Titel: Colophonius Regenschein Verfasst am: 09. Sep 2021 22:06 Titel: |
 |
|
Danke für die Antworten.
Da das Problem etwas Verwirrung erzeugt hat nochmal kurz die Problemstellung:
Ich suche die Ladungsverteilung eines leitenden Körpers der an einer Spannung  liegt, also ein Ladungsüberschuss hat. Zum Beispiel ein metallischer Kegel an einer 10V Spannungsquelle. Wir erwarten, dass an der Spitze des Kegels sich eine höhere Ladungsdichte befindet als am stumpfen Ende. Um das numerisch am Computer zu berechnen unterteile ich die Form in Voxel, die jeweils eine Ladung als Eigenschaft haben. Diese Ladungen suche ich. Der Voxel an der Kegelspitze sollte also den höchsten Ladungswert haben. Mit den Voxeln will ich jede x-beliebige Form dann approximieren können. liegt, also ein Ladungsüberschuss hat. Zum Beispiel ein metallischer Kegel an einer 10V Spannungsquelle. Wir erwarten, dass an der Spitze des Kegels sich eine höhere Ladungsdichte befindet als am stumpfen Ende. Um das numerisch am Computer zu berechnen unterteile ich die Form in Voxel, die jeweils eine Ladung als Eigenschaft haben. Diese Ladungen suche ich. Der Voxel an der Kegelspitze sollte also den höchsten Ladungswert haben. Mit den Voxeln will ich jede x-beliebige Form dann approximieren können.
Bei der ersten Antwort kam auf, dass die Bedingung  problematisch sein könnte und eher eine Probeladung zu betrachten sei. Was dann auch mein Problem löste, dass sich Ladungen vermehrt auch in der Mitte aufhalten (siehe Beispiel oben mit 3 Voxeln). problematisch sein könnte und eher eine Probeladung zu betrachten sei. Was dann auch mein Problem löste, dass sich Ladungen vermehrt auch in der Mitte aufhalten (siehe Beispiel oben mit 3 Voxeln).
Neuer Ansatz (2 benachbarte Voxel):

Wenn ein Voxel an einer der sechs Seiten keinen Nachbarn hat setze ich eine Ladung  auf diese äußere Fläche. Auf halber Strecke setze ich auf diese äußere Fläche. Auf halber Strecke setze ich  . Diese dient als Zwangsbedingung . Diese dient als Zwangsbedingung  . Somit bekomme ich das Gleichungssystem . Somit bekomme ich das Gleichungssystem  . Die Summe der Coulombpotentiale aller Ladungen sollte also in jedem . Die Summe der Coulombpotentiale aller Ladungen sollte also in jedem  der externen Spannung entsprechen. Da der externen Spannung entsprechen. Da  nicht mehr Null ist für nicht mehr Null ist für  , muss ich diesen Fall nicht mehr ignorieren. Da ich genauso viele N Ladungen wie N Potentialpunkte habe, bekomme ich N Gleichungen mit N Unbekannten. , muss ich diesen Fall nicht mehr ignorieren. Da ich genauso viele N Ladungen wie N Potentialpunkte habe, bekomme ich N Gleichungen mit N Unbekannten.
Das Ergebnis sieht jetzt sinnvoll aus. An Kanten und Ecken habe ich viele Ladungen, auf großen Flächen fast keine. Wie exakt das Ergebnis ist muss ich noch testen. Eventuell muss ich noch innere eingeschlossene Flächen in einem Körper ignorieren.
Offene Fragen: Was wäre wenn ich die Anzahl Voxel gegen unendlich laufen lassen würde und die Kantenlänge gegen Null? Dann würde die Summe zu einem Integral werden. Die Matrix mit den Inversen Entfernungen enthält ja die geometrischen Informationen. Diese müsste dann in eine Flächenfunktion übergehen, Das Ergebnis wäre dann die Ladungsflächendichte. Meine Ladungen beziehen sich ja momentan auch immer auf eine Fläche. Gibt es so eine Funktion? Macht das Sinn?
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
 DrStupid Verfasst am: 10. Sep 2021 09:50 Titel: DrStupid Verfasst am: 10. Sep 2021 09:50 Titel: |
 |
|
| Colophonius Regenschein hat Folgendes geschrieben: | Auf halber Strecke setze ich  . . |
Warum nur auf halber Strecke? Das Potential ist doch im gesamten Körper konstant. Eventuell kann man das Problem lösen, indem man die Positionen zufällig wählt und dann den Mitelwert der resultierenden Ladungsverteilungen verwendet. Dann könnte man auch einschätzen, wie glaubhaft das Ergebnis ist. So richtig schön ist das aber nicht.
Ich würde das Problem ganz anders angehen: Da das Potentiel im Inneren des Körpers konstant ist, gibt es dort auch kein elektrisches Feld und damit auch keine Ladungsdichte. Alle Ladungen müssen sich auf der Oberfläche verteilen und das elektrische Feld steht dort überall senkrecht auf der Oberfläche. Da liegt es nahe, sich von vorn herein auf die Oberfläche zu beschränken.
Ein einfacher Ansatz besteht darin, die Oberfläche aus Dreiecken zusammenzustückeln und die Ladungen so auf die Eckpunkte zu verteilen, dass alle das gleiche Potential haben. Das sollte auch Ressourcen sparen, weil man zumindest für einfache Geometrien viel weniger Dreiecke als Voxel benötigt.
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
 DrStupid Verfasst am: 14. Sep 2021 20:45 Titel: DrStupid Verfasst am: 14. Sep 2021 20:45 Titel: |
 |
|
Ich habe jetzt mal einen alten Quellcode herausgekramt und für dieses Problem umgeschrieben. Für die Berechnung des Potentials habe ich die Ladungsdichte zwischen den Ecken der Dreiecke linear interpoliert und dann das Potential numerisch über die Fläche integriert. Es ist zwar auch in diesem Fall möglich, die Ladungsdichte in den Eckpunkten des Polyeders durch Lösung eines linearen Gleichungssystems zu berechnen, aber das war mir zu kompliziert (vielleicht mache ich das später). Stattdessen habe ich sie iterativ berechnet.
Um das Programm zu testen, habe ich zuerst die Ladungsverteilung einer Kugel mit einem Meter Radius und einem Potential von 1 V berechnet. Das Ergebnis ist eine Ladungsdichte von 8,87±0,09 pC/m² und eine Gesamtladung von 111,17 pC. Das ist weniger als 0,1 % vom theoretischen Wert entfernt.
Als nächstes habe ich es mit einem gleich großen Dodekaeder probiert (siehe Anhang). Da erhalte ich eine Ladungsdichte zwischen 4,23 pC/m² auf den Flächen und 42,2 pC/m² an den Ecken. Die Gesamtladung beträgt 98 pC.
Bei Körpern mit scharfen Kanten und Ecken hängt die berechnete Ladungsdichte deutlich von der räumlichen Diskretisierung ab. Das liegt daran, dass es sich um die mittlere Ladungsdichte im Bereich um die Eckpunkte der Dreiecke handelt, aus denen sich die Oberfläche zusammensetzt. Wo sich die Ladungsdichte nicht-linear ändert, da hängt ihr Mittelwert von der Größe dieses Bereiches ab.
| Beschreibung: |
|
| Dateigröße: |
40.19 KB |
| Angeschaut: |
862 mal |

|
|
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
 DrStupid Verfasst am: 18. Sep 2021 00:11 Titel: DrStupid Verfasst am: 18. Sep 2021 00:11 Titel: |
 |
|
Jetzt habe ich auch das lineare Geichungssystem hinbekommen. Leider funktioniert das nur für den Fall, dass alle Spannungen vorgeben sind. Wenn ich stattdessen die Ladungen festlege, dann kann ich zwar ein entsprechendes Gleichungssystem aufstellen, aber die Solver, mit denen ich es probiert habe (Jacobi und SOR), kommen damit nicht klar. Mir ist auch aufgefallen, dass die Verfahren zu Oszillationen neigen, die mit wachsender Auflösung der Gitter zunehmen. Mit SOR bekommt man das zwar gut in den Griff, aber je robuster man es macht, um so langsamer konvergiert es.
Momentan umgehe ich das Problem, indem ich abwechselnd die Spannungen ändere und dann die zugehörige Ladungsverteilung berechne, bis alle vorgegebenen Ladungen erreicht sind. So kann ich dann z.B. berechnen, wie sich die Ladungen auf einem Körper mit vorgegebener Gesamtladung verteilt, der sich zwischen zwei Körpern mit vorgegebenen Spannungen befindet:
| Beschreibung: |
|
| Dateigröße: |
26.84 KB |
| Angeschaut: |
829 mal |
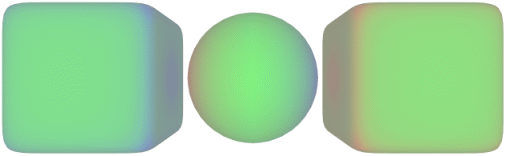
|
|
|
 |
|
|
















 .
.