| Autor |
Nachricht |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 17. Aug 2021 20:14 Titel: Riemann'sche Normalkoordinaten vs. lokal ebenes System schnudl Verfasst am: 17. Aug 2021 20:14 Titel: Riemann'sche Normalkoordinaten vs. lokal ebenes System |
 |
|
Gestern stellte ich eine Frage zu einem lokalen Inertialsystem in der ART. Die Frage stellte sich nach einiger Überlegung als Unsinn heraus, da ich noch nicht ganz verstanden hatte, was man unter einer flachen Metrik versteht und diese falsch angewandt hatte. Aus diesem Grund habe ich die Frage gelöscht 
Nach einiger Recherche habe ich folgende Definitionen gefunden:
Im Rebhan steht:
Ein Koordinatensystem  , für das im Punkt , für das im Punkt 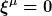 die Bedingungen die Bedingungen
 = \eta_{\mu \nu})
und
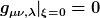
efüllt sind, nennt man lokal ebenes System.
Soweit habe ich das auch "verstanden".
Nun gibt es aber auch den Begriff "Riemann'sche Normalkoordinaten". In diesem Video wird das sehr anschaulich und ziemlich elementar erklärt: https://vimeo.com/486542612 als Quelle.
In Minute 12 schreibt der Vortragende die Transformationsgleichung auf Basis der Christoffel Symbole an. Auch wenn das vielleicht nicht so ganz sauber hergeleitet und durchaus ein wenig gezaubert wird, ist es mir dennoch klar. Vorausgesetzt wird scheinbar, dass ausgehend von einem Punkt P immer eine eindeutige Geodäte durch einen hinreichend nahen zweiten Punkt Q gehen muss. Der mit dem Abstand PQ multiplizierte Tangentenvektor an P sind die Riemann'schen Koordinaten. Er zeigt weiters in Minute 15, dass die Christoffel Symbole im Ursprung der neuen Koordinaten verschwinden und man aufgrund der angegebenen Transformation 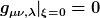 erzwungen hat. erzwungen hat.
Nun kann man durch eine weitere lineare Transformation (Minute 20) auch noch erreichen, dass die Metrik dieser Riemannschen Koordinaten (RCS) sich auf die Minkowski Metrik transformiert. Er spricht dann von Riemann'schen Normalkoordinaten (RNCS).
Dazu drei Fragen:
1) Wieso ist diese Transformation auf die Diagonalform immer möglich? Dass eine Matrix auf Diagonalform transformiert werden kann, leuchtet mir ein - aber wieso ist es hier auch möglich auf die Minkowski Form zu transformieren,mit -1 und drei mal 1 in der Diagonale? Sicher eine der vielen Lücken in linearer Algebra 
2) Darum geht's mir eigentlich: Ist das, was in diesem Video als Riemann'sche Normalkoordinaten bezeichnet wird, das selbe, was ich im Rebhan als lokal ebenes System gefunden habe? Ich gehe eigentlich davon aus, bin mir aber nicht so ganz sicher...
3) So wie ich das sehe, wird im gewählten Koodinatenursprung das Gravitationsfeld wegtransformiert und wir haben dort ein lokales Intertialsystem, indem der Ursprung des Systems quasi auf der Geodäten "mitfällt". Deshalb auch die tensorielle Analogie zu s = a/2*t² in der Transformation. Ist diese Sicht richtig?
Ich bin hier einigermaßen verwirrt und muss das erst alles verinnerlichen. Ich stehe am Anfang...
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe)
Zuletzt bearbeitet von schnudl am 18. Aug 2021 13:39, insgesamt einmal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Aug 2021 21:17 Titel: Re: Riemann'sche Normalkoordinaten vs. lokal ebenes System index_razor Verfasst am: 17. Aug 2021 21:17 Titel: Re: Riemann'sche Normalkoordinaten vs. lokal ebenes System |
 |
|
| schnudl hat Folgendes geschrieben: |
Dazu zwei Fragen:
1) Wieso ist diese Transformation auf die Diagonalform immer möglich? Dass eine Matrix auf Diagonalform transformiert werden kann, leuchtet mir ein - aber wieso ist es hier auch möglich auf die Minkowski Form zu transformieren,mit -1 und drei mal 1 in der Diagonale? Sicher eine der vielen Lücken in linearer Algebra 
|
Jede symmetrische Matrix kann mittels orthogonaler Transformation auf Diagonalform gebracht werden, egal welche Einträge auf der Diagonale stehen. Da die Transformation linear ist, ändert sich dann nichts mehr an =0) . .
| Zitat: |
2) Darum geht's mir eigentlich: Ist das, was in diesem Video als Riemann'sche Normalkoordinaten bezeichnet wird, das selbe, was ich im Rebhan als lokal ebenes System gefunden habe? Ich gehe eigentlich davon aus, bin mir aber nicht so ganz sicher...
|
Ich glaube ich habe vorher noch nie die Bezeichnung "lokal ebenes System" gehört. Aber deiner Beschreibung nach handelt es sich wohl einfach um ein lokales Inertialsystem. Und Riemannsche Normalkoordinaten bilden tatsächlich ein lokales Inertialsystem.
| Zitat: |
3) So wie ich das sehe, wird im gewählten Koodinatenursprung das Gravitationsfeld wegtransformiert und wir haben dort ein lokales Intertialsystem, indem der Ursprung des Systems quasi auf der Geodäten "mitfällt". Deshalb auch die tensorielle Analogie zu s = a/2*t² in der Transformation. Ist diese Sicht richtig?
|
Die Frage verstehe ich nicht. Was hat das ganze mit  zu tun? zu tun?
In einem lokalen Inertialsysteme verschwinden alle Trägheitskräfte und die Gravitation im Ursprung. Dort hat ein Teilchen also die Bewegungsgleichung

wobei F alle nichtgravitativen Wechselwirkungen beschreibt. |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 18. Aug 2021 07:25 Titel: schnudl Verfasst am: 18. Aug 2021 07:25 Titel: |
 |
|
| Zitat: | | Jede symmetrische Matrix kann mittels orthogonaler Transformation auf Diagonalform gebracht werden, egal welche Einträge auf der Diagonale stehen. |
Das macht nun Sinn. Habe symmetrisch übersehen.
| Zitat: | | Die Frage verstehe ich nicht. Was hat das ganze mit s=a/2*t² zu tun? |
Wenn ich die Schwerkraft auf der Erde wegtransformieren will, geht das über ein mitfallendes Koordinatensystem:

Das hat irgendwie eine "strukturelle Ähnlichkeit" mit der Transformation, die im Video verwendet wired:

Vielleicht ist diese "Ähnlichkeit" aber nicht sehr tiefschürfend. Ist mir nur aufgefallen.
In meinem Rebhan werden die Christoffel Symbole als metrischer Zusammenhang durch einen Ansatz dieser Art übrigens eingeführt und deren Eigenschaften dann hergeleitet. Im Video werden die schon als bekannt vorausgesetzt.vorausgesetzt und über den Paralleltransport und die kovariante Ableitung definiert. Scheinbar kann man sich hier auf verschiedene Arten annähern.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18018
|
 TomS Verfasst am: 18. Aug 2021 09:22 Titel: TomS Verfasst am: 18. Aug 2021 09:22 Titel: |
 |
|
Habe die Frage zur Quantengravitation hierher verschoben https://www.physikerboard.de/ptopic,362516.html#362516
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 18. Aug 2021 15:03 Titel: index_razor Verfasst am: 18. Aug 2021 15:03 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: |
| Zitat: | | Die Frage verstehe ich nicht. Was hat das ganze mit s=a/2*t² zu tun? |
Wenn ich die Schwerkraft auf der Erde wegtransformieren will, geht das über ein mitfallendes Koordinatensystem:

Das hat irgendwie eine "strukturelle Ähnlichkeit" mit der Transformation, die im Video verwendet wired:

Vielleicht ist diese "Ähnlichkeit" aber nicht sehr tiefschürfend. Ist mir nur aufgefallen.
|
Doch, die Analogie stimmt schon. Am leichtesten sieht man das wohl daran, daß man in einem drehungsfreihen Koordinatensystem in der Newtonschen Mechanik  (i=1,2,3) und (i=1,2,3) und  für alle anderen Christoffelsymbole setzen kann. für alle anderen Christoffelsymbole setzen kann.
Mir war nur nicht klar, daß du von einer Koordinatentransformation redest. Ich dachte es ging um die Bahnkurve eines Teilchens im lokalen Inertialsystem. |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 19. Aug 2021 12:33 Titel: schnudl Verfasst am: 19. Aug 2021 12:33 Titel: |
 |
|
So ganz habe ich es immer noch nicht verstanden:
Durch einen beliebigen Punkt P einer Raumzeit gehen i.A. unendlich viele Geodäten. Jede dieser Kurven wäre somit ein Kandidat für ein mitfallendes Koordinatensystem, das für einen Beobachter in seinem Ursprung inertial ist.
Im homogenen Erdfeld gibt es beispielsweise eine Geodäte, die entlang z fällt, aber auch eine parabelförmige Geodäte mit einer x-Komponente. Beides wären Kandidaten für ein mitbewegtes Inertialsystem.
Was zeichnet nun ein Riemannsches Normalkordinatensystem RNCS in P gegenüber einem beliebigen anderen Koordinatensystem aus, welches ebenfalls in P inertial ist (siehe Parabelvergleich von oben)?
Ist es einzig und allein die Tatsache, dass der Referenzpunkt P, auf den sich das Bezugssystem bezieht (und wo wir die Gravitation lokal wegtransformieren wollen) im RNCS momentan (bei t=0) in Ruhe ist? Das würde ich nämlich herauslesen - aber ist das wirklich alles oder übersehe ich hier etwas? Ich habe die ganze Zeit gedacht, dass es für einen Punkt genau ein eindeutiges lokales Inertialsystem gäbe, klarerweise gibt es aber unendlich viele und das RNCS ist davon ein besonderes, wo sich der Referenzpunkt (momentan) nicht bewegt (aber natürlich von Anfang an beschleunigt ist)? Sehe ich das so richtig und falls ja, welche physikalischen Vorteile erschließen sich durch die Verwednung dieses speziellen Bezugssystems?
Für mich ist das alles sehr verwirrend...sobald ich denke, es verstanden zu haben, kommen drei neue Fragen... 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 19. Aug 2021 15:09 Titel: index_razor Verfasst am: 19. Aug 2021 15:09 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: | So ganz habe ich es immer noch nicht verstanden:
Durch einen beliebigen Punkt P einer Raumzeit gehen i.A. unendlich viele Geodäten. Jede dieser Kurven wäre somit ein Kandidat für ein mitfallendes Koordinatensystem, das für einen Beobachter in seinem Ursprung inertial ist.
|
Jede davon ist ja auch ein Kandidat für ein System aus Riemannschen Normalkoordinaten. Genauer gesagt, an jedem Ereignis P kann man eine beliebige Lorentzbasis wählen und mit ihr ein anderes System aus Riemannschen Normalkoordinaten konstruieren. Und alle diese Normalkoordinaten bilden lokale Inertialsysteme, deren Relativgeschwindigkeiten zueinander von der Wahl des Zeitvektors abhängt.
| Zitat: |
Was zeichnet nun ein Riemannsches Normalkordinatensystem RNCS in P gegenüber einem beliebigen anderen Koordinatensystem aus, welches ebenfalls in P inertial ist (siehe Parabelvergleich von oben)?
|
Also zunächst mal kannst sowohl für das in z-Richtung als auch für das parabelförmig fallende Objekt ein Riemannsches Normalkoordinatensystem konstruieren. Du scheinst hier also irgendwie eine Scheinalternative zu betrachten. Natürlich kann es auch wiederum für jede dieser Kurven ein lokales Inertialsystem geben, das nicht aus Riemannschen Normalkoordinaten besteht. Der Unterschied bestünde dann in der Form der Komponenten des Krümmungstensors. Eine Besonderheit an Riemannschen Normalkoordinaten ist z.B. die simple Form des Krümmungstensors im Referenzereignis:
 = g_{\mu\tau, \nu\lambda}(P) - g_{\mu\lambda, \nu\tau}(P).)
| Zitat: |
Ist es einzig und allein die Tatsache, dass der Referenzpunkt P, auf den sich das Bezugssystem bezieht (und wo wir die Gravitation lokal wegtransformieren wollen) im RNCS momentan (bei t=0) in Ruhe ist?
|
P ist irgendein festes Ereignis. Es ist nicht sinnvoll davon zu reden, daß ein Ereignis in irgendeinem Koordinatensystem ruht oder bewegt ist. Zu jedem Ereignis gehört höchstens eine Zeit- und drei Raumkoordinaten. Um Bewegung zu beschreiben, benötigt man eine Folge von Ereignissen, die z.B. durch verschiedene Zeitpunkte parametrisiert wird. |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 19. Aug 2021 18:43 Titel: schnudl Verfasst am: 19. Aug 2021 18:43 Titel: |
 |
|
Zuerst mal zu
| Zitat: | | Jede davon ist ja auch ein Kandidat für ein System aus Riemannsche Normalkoordinaten. |
Das verstehe ich nun insofern nicht, da die Konstruktion der RNC entsprechend dem Vorgehen aus dem Video lautet:

Das ist ja eindeutig. Hier wird von keinem Kandidaten ausgegangen, sondern die Auswertung des Ausdrucks ergibt eine eindeutige Transformation y=y(x).
Auch das Konstruktionsprinzip, welches man sonst findet ist eindeutig:
1) wähle die eindeutige Geodäte g(s) von P nach Q
2) Bestimme den Abstand s von P nach Q
3) Bestimme den Tangentenvektor t auf dieser Geodäte im Punkt P
4) Die Komponenten der RNC von Q sind die Komponenten von s*t
Das ist auch eindeutig. Wo habe ich hier eine Freiheit? Es wird ga gerade jene Geodäte ausgewählt, die P mit Q verbindet.
Sorry, dass ich damit nerve...ich will es aber wirklich verstehen.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 19. Aug 2021 19:08 Titel: index_razor Verfasst am: 19. Aug 2021 19:08 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: | Zuerst mal zu
| Zitat: | | Jede davon ist ja auch ein Kandidat für ein System aus Riemannsche Normalkoordinaten. |
Das verstehe ich nun insofern nicht, da die Konstruktion der RNC entsprechend dem Vorgehen aus dem Video lautet:

Das ist ja eindeutig.
|
Das ist genauso wenig eindeutig, wie das ursprüngliche Koordinatensystem  in der Umgebung von P eindeutig war. Wenn du mit anderen Koordinaten startest, kannst du die Konstruktion genauso durchführen und landest im allgemeinen bei anderen Riemannschen Normalkoordinaten. in der Umgebung von P eindeutig war. Wenn du mit anderen Koordinaten startest, kannst du die Konstruktion genauso durchführen und landest im allgemeinen bei anderen Riemannschen Normalkoordinaten.
| Zitat: |
Hier wird von keinem Kandidaten ausgegangen, sondern die Auswertung des Ausdrucks ergibt eine eindeutige Transformation y=y(x).
|
Nein, aber es wird vollkommen äquivalent von einem beliebigen Koordinatensystem ausgegangen.
| Zitat: |
Auch das Konstruktionsprinzip, welches man sonst findet ist eindeutig:
1) wähle die eindeutige Geodäte g(s) von P nach Q
2) Bestimme den Abstand s von P nach Q
3) Bestimme den Tangentenvektor t auf dieser Geodäte im Punkt P
4) Die Komponenten der RNC von Q sind die Komponenten von s*t
Das ist auch eindeutig.
|
Nein, was die "Komponenten" von t (oder st) sind, ist höchst uneindeutig. Es hängt von der Wahl einer Basis bei P ab.
| Zitat: |
Sorry, dass ich damit nerve...ich will es aber wirklich verstehen. |
Du nervst keineswegs. Ich hoffe, daß ich helfen kann.
Zuletzt bearbeitet von index_razor am 20. Aug 2021 10:35, insgesamt einmal bearbeitet |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 19. Aug 2021 20:37 Titel: schnudl Verfasst am: 19. Aug 2021 20:37 Titel: |
 |
|
Ich bin momentan nicht mehr sehr aufnahmefähig, aber so wie ich das sehe, geht es hier ja um den Tangentialraum im Punkt P. Um die RNC entsprechend der Konstruktionsvorschrift für den Punkt Q in der Nähe von P zu erhalten, legt man eine Geodäte von P nach Q. Der mit dem Abstand s multiplizierte Tangentenvektor im Punkt P hat dann als Komponenten per Definition die Koordinaten von Q in den RNC.
Besteht die von dir angesprochene Freiheit darin, auf welche Weise ich ein "Vierbein" in der Tangentialebene um P aufstelle bzw. orientiere um diese zu kartieren?
Wenn ich nun sage ich hätte es verstanden, bin ich mir sicher, dass ich morgen mit einer neuen Frage aufwache. 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 19. Aug 2021 20:56 Titel: index_razor Verfasst am: 19. Aug 2021 20:56 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: | Um die RNC entsprechend der Konstruktionsvorschrift für den Punkt Q in der Nähe von P zu erhalten, legt man eine Geodäte von P nach Q. Der mit dem Abstand s multiplizierte Tangentenvektor im Punkt P hat dann als Komponenten per Definition die Koordinaten von Q in den RNC.
Besteht die von dir angesprochene Freiheit darin, auf welche Weise ich ein "Vierbein" in der Tangentialebene um P aufstelle bzw. orientiere um diese zu kartieren? |
Ja, natürlich. Wie sonst definierst du "die Komponenten" des Tangentialvektors t? Diese Komponenten -- und damit auch die Koordinaten des Punktes Q entlang der Geodäte in Richtung t -- hängen davon ab, welche Basis du in P gewählt hast. |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 19. Aug 2021 21:27 Titel: schnudl Verfasst am: 19. Aug 2021 21:27 Titel: |
 |
|
Ich verstehe das nun so:
Allen möglichen Ausrichtungen einer Tetrade am Tangentenraum entsprechen dann verschiedene inertiale Bezugssysteme mit einer Minkowski Metrik. Wie unterscheiden diese sich dann physikalisch voneinander?
Sind das dann Koordinatensysteme, die durch eine allgemeine Lorentz-Transformation, also einer 4-D Drehung ineinander übergehen? Also entweder bloß durch räumliche Drehungen (Zeitachse fix) oder Boosts mit Relativgeschwindigkeit? Inertialsystem bleibt aber dadurch Inertialsystem...so hab ich das noch nie betrachtet - es macht aber (vorläufig) Sinn.
Ist das richtig? Falls ja, war das eine schwere Geburt...falls nein, hab ich keinen Kopf mehr dafür.
Danke- du hast mir einiges klar gemacht.
 
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 20. Aug 2021 08:59 Titel: index_razor Verfasst am: 20. Aug 2021 08:59 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: | Ich verstehe das nun so:
Allen möglichen Ausrichtungen einer Tetrade am Tangentenraum entsprechen dann verschiedene inertiale Bezugssysteme mit einer Minkowski Metrik.
|
Ja, wenn die Basis eine Lorentzbasis ist, also aus einem zeitartigen und 3 raumartigen Vektoren besteht, die alle orthogonal zueinander stehen. Von diesem Fall bin ich bis jetzt immer implizit ausgegangen. Für andere Basen (z.B. mit zwei lichtartigen Vektoren) hätte man immer noch Normalkoordinaten, aber würde sie nicht als lokales Inertialsystem bezeichnen.
| Zitat: |
Wie unterscheiden diese sich dann physikalisch voneinander?
|
Durch ihre momentane Relativgeschwindigkeit im Ereignis P oder durch die Orientierung der räumlichen Achsen. Wenn man sie als Ruhesysteme von Beobachtern betrachtet, deren momentane Vierergeschwindigkeit dem zeitartigen Vektor der Basis entspricht, dann fallen alle diese Beobachter mit verschiedenen Geschwindigkeiten frei durch das Ereignis P.
| Zitat: |
Sind das dann Koordinatensysteme, die durch eine allgemeine Lorentz-Transformation, also einer 4-D Drehung ineinander übergehen?
|
Die Lorentzbasen im Punkt P gehen durch Lorentztransformation auseinander hervor. Die Koordinatenwerte in größerer Entfernung von P nicht unbedingt, sondern nur so lange man die Krümmung vernachlässigen kann.
| Zitat: |
Also entweder bloß durch räumliche Drehungen (Zeitachse fix) oder Boosts mit Relativgeschwindigkeit? Inertialsystem bleibt aber dadurch Inertialsystem...so hab ich das noch nie betrachtet - es macht aber (vorläufig) Sinn.
|
Ja, in einer kleinen Umgebung von P kann man das so sehen. |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 20. Aug 2021 20:34 Titel: schnudl Verfasst am: 20. Aug 2021 20:34 Titel: |
 |
|
Danke einmal für die Antworten...
Jetzt ist da noch eine Frage aufgetaucht:
Diese Transformation vom System S|x auf Normalkoordinaten S'|y bezüglich eines Punkts P war ja (P habe in S die Koordinaten Null)
 \cdot x^\alpha x^\beta)
Nun wollte ich fragen, wie sich der Ursprung y=0 dieses neuen Koordinatensystems in S bewegt. An der Stelle P müsste die Weltlinie des Koordinatenursprungs meiner Meinung nach entsprechend einer lokalen Geodäten "frei durchfallen" bzw. dort eine lokale Geodäte sein (ist ja der Sinn dahinter). Ich wollte das kurz überprüfen und habe daher erst einmal y=0 gesetzt, um mich in den Ursprung von S' zu setzen.
 \cdot x^\alpha x^\beta)
Das sollte nun die Weltlinie des Koordinatenurprungs beschreiben bzw. der Gleichung einer Geodäten bei x=P genügen. Ich leite daher einmal ab:
 \cdot \dot x^\alpha x^\beta)
Laut Voraussetzung sind die Koordinaten von P alle Null: wenn ich aber im letzten Ausdruck 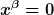 setze, erhalte ich setze, erhalte ich

Wo ist der Fehler? Die 4er Geschwindigkeit kann ja nicht Null werden. Irgendwo hab ich was ganz kapitales übersehen oder ich hab ein dickes Brett vor dem Kopf. 
Idee: Muss ich hier etwa die kovariante Ableitung verwenden?
Also ersetzen
 )
Nur falls ja: warum? Ich habe ja bei der ersten Variante nur die Kettenregel angewandt, was ist daran also falsch? Ist es, weil sich die Metrik entlang der Bahnkurve ändert und ich das sonst nicht berücksichten würde?
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 21. Aug 2021 08:56 Titel: index_razor Verfasst am: 21. Aug 2021 08:56 Titel: |
 |
|
| schnudl hat Folgendes geschrieben: |
Diese Transformation vom System S|x auf Normalkoordinaten S'|y bezüglich eines Punkts P war ja (P habe in S die Koordinaten Null)
 \cdot x^\alpha x^\beta)
Nun wollte ich fragen, wie sich der Ursprung y=0 dieses neuen Koordinatensystems in S bewegt.
|
Der Ursprung y=0 ist ein einziges Ereignis. Er bewegt sich gar nicht. Da y=0 nur in einem einzigen Punkt gilt, kannst du diese Gleichung auch nicht einfach ableiten.
In Normalkoordinaten gibt es aber eine zeitartige Geodäte, die in der Nähe des Ursprungs die Form =(t, 0, 0, 0)) hat. Diese Kurve repräsentiert einen frei fallenden Beobachter, der an den räumlichen Koordinaten hat. Diese Kurve repräsentiert einen frei fallenden Beobachter, der an den räumlichen Koordinaten  ruht. (Und dessen Vierergeschwindigkeit bei y=0 natürlich ruht. (Und dessen Vierergeschwindigkeit bei y=0 natürlich ) ist.) ist.)
Übrigens gilt
x^n x^m+\ldots)
nur bis zur zweiten Ordnung in x. Da du die Gleichung immer so verwendet hast, als gälte sie exakt, nahm ich bis jetzt an, daß du von der Umkehrung redest
y^n y^m,)
und dachte folglich x und nicht y wären die Normalkoordinaten. Ich hoffe das hat nicht für Verwirrung gesorgt.
Um die Weltlinie des in Normalkoordinaten y ruhenden Beobachters in den Koordinaten x auszurechnen, kann man am besten die zweite Gleichung benutzen. Man muß nur  einsetzen, also einsetzen, also
 = t\delta^{i0} - \frac{1}{2}\Gamma^i_{00}(P)t^2.) |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 22. Aug 2021 10:06 Titel: index_razor Verfasst am: 22. Aug 2021 10:06 Titel: |
 |
|
Oder um es nochmal auf den Punkt zu bringen: Der Fehler besteht in der Annahme, daß der Zusammenhang
 + \frac{1}{2}\Gamma^i_{nm}(P)\ x^n(t) x^m(t) + \ldots)
identisch in t gilt, also nach t abgeleitet werden kann. Das ist aber nicht der Fall, falls x(t) die Weltlinie eines Beobachters beschreiben soll. In diesem Fall kann sie nur an einer Stelle gelten, also nur für einen einzigen Wert von t. |
|
 |
schnudl
Moderator

Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 22. Aug 2021 10:50 Titel: schnudl Verfasst am: 22. Aug 2021 10:50 Titel: |
 |
|
Ich mache immer wieder den gleichen Fehler und stelle mir ein räumliches Koordinstensystem vor...natürlich war das Ableiten Quatsch. Ich weiß nicht, wie oft mir das noch passiert, indem ich übersehe, dass sich ein Punkt in 4D nicht bewegt...
Zumindest bin ich nun zufrieden, dass sich das aufgeklärt hat.
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
|
|






















