| Autor |
Nachricht |
BrunoBaer
Anmeldungsdatum: 05.11.2020
Beiträge: 5
|
 BrunoBaer Verfasst am: 05. Nov 2020 18:39 Titel: Kontinuitätsgleichung vs. Poiseuille BrunoBaer Verfasst am: 05. Nov 2020 18:39 Titel: Kontinuitätsgleichung vs. Poiseuille |
 |
|
Meine Frage:
Hallo liebe Physiker und Physikerinnen,
es geht um die Vereinbarkeit des Poiseuille'schen Gesetzes und der Kontinuitätsgleichung. Ich bin Mediziner und in meiner Physiologie-Vorlesung (Kreislauf) haben wir uns mit der Kontinuitätsgleichung und dem Poiseuille'schen Gesetz befasst. Doch ich sehe einen Widerspruch zwischen den beiden Gesetzen. Leider finde ich auch in den einschlägigen Lehrbüchern der Physiologie darauf keine Antwort.
Das Poiseuille-Gesetz besagt, dass eine Abnahme der Querschnittsfläche zu einer Abnahme der Durchflussrate führt (aufgrund des r4-Faktors im Zähler, wobei r der Querschnittsradius ist).
Die Kontinuitätsgleichung besagt, dass die Durchflussrate in allen Bereichen eines Rohres konstant sein muss, unabhängig von der Querschnittsfläche (d.h. eine Verringerung der Querschnittsfläche (Verengung eines Rohres) führt zu einer Erhöhung der Geschwindigkeit, um die Durchflussrate aufrechtzuerhalten).
Wie arbeiten diese beiden Ideen zusammen? Wie kann es sein, dass eine Verringerung der Querschnittsfläche in einer Gleichung zu einer Verringerung der Durchflussrate führt (Poiseuille'sches Gesetz), in einer anderen Gleichung jedoch keine Auswirkungen aufgrund von Geschwindigkeitsanpassungen hat (Kontinuitätsgleichung)? Ich habe Schwierigkeiten zu verstehen, warum sich diese beiden Ideen nicht widersprechen. Es ist auch durchaus möglich, dass ich etwas völlig missverstanden habe.
In anderen Worten: Wenn ein Rohr (im medizinischen Kontext: ein Blutgefäß) kleiner wird, nimmt die Geschwindigkeit entsprechend der Kontinuität zu, um die kleinere Fläche auszugleichen (Kontinuitätsprinzip). Nach Poiseuille nimmt die Durchflussrate jedoch um r^4 ab und bleibt eben nicht konstant.
Wo ist mein Denkfehler?
Über eine klare und ausführliche Beantwortung der Frage würde ich mich sehr freuen.
Mit freundlichen Grüßen
Bruno
Meine Ideen:
Warum widersprechen sich Kontinuitätsgleichung und Poiseuille nicht? |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 05. Nov 2020 19:06 Titel: Nils Hoppenstedt Verfasst am: 05. Nov 2020 19:06 Titel: |
 |
|
Hallo,
Beim Hagen-Poiseuille-Gesetz betrachtet man verschiedene Rohrleitungen mit unterschiedlichen Querschnitten und bei der Kontinuitätsgleichung betrachtet man unterschiedlichen Stellen innerhalb des selben Rohres mit eventuell variierendem Querschnitt.
Viele Grüße,
Nils |
|
 |
Bruno-Baer
Gast
|
 Bruno-Baer Verfasst am: 05. Nov 2020 19:47 Titel: Rückfrage Bruno-Baer Verfasst am: 05. Nov 2020 19:47 Titel: Rückfrage |
 |
|
| Nils Hoppenstedt hat Folgendes geschrieben: | Hallo,
Beim Hagen-Poiseuille-Gesetz betrachtet man verschiedene Rohrleitungen mit unterschiedlichen Querschnitten und bei der Kontinuitätsgleichung betrachtete man unterschiedlichen Stellen innerhalb des selben Rohres mit eventuell variierendem Querschnitt.
Viele Grüße,
Nils |
Hallo, Nils,
zunächst einmal vielen lieben Dank für die Antwort!
Wenn es um die Fließgeschwindigkeit des Blutes in der Aorta im Vergleich zu der Fließgeschwindigkeit in den Kapillaren geht, wird mit dem Kontinuitätsprinzip gerechnent. Aufgrund des viel größeren Gesamtquerschnitts von den Kapillaren ist daher die Blutgeschwindigkeit innerhalb der Kapillaren deutlich geringer. Da hier das Kontinuitätsgesetz verwendet wird, wird deiner Logik nach das Gefäßsystem als ein Rohr mit unterschiedlichen Querschnitten betrachtet.
Wenn es jedoch um Gefäßverengungen geht, wird dann aber mit dem Hagen-Poiseuille-Gesetz gerechnet. So heißt es dann beispielsweise, dass die Flussrate um 1/16 abnimmt, da sich der Gefäßradius halbiert. Doch warum wird hier auf einmal dieses Gesetzt verwendet und nicht die Kontinuitätsgleichung? Warum wird hier das Gefäß als zwei unterschiedliche Rohre betrachtet und daher das Hagen-Poiseuille-Gesetz verwendet? Es handelt sich doch trotzdem noch um ein Rohr, das jedoch an unterschiedlichen Stellen verschiedene Durchmesser hat.
Aus irgendeinem Grund darf hier das Kontinuitätsgesetz nicht verwendet werden. Schließlich wären dann auch keine Behandlungen von Gefäßverengungen nötig, da nach dem Kontinuitätsgesetz schließlich die Flussrate gleich groß bleiben würde und somit die Organversorgung sichergestellt wäre. Das ist aber nicht der Fall! Doch wie kann man begründen, dass hier das Hagen-Poiseuille-Gesetz und nicht das Kontinuitätsgesetz verwendet wird?
Warum wird in dem ersten Fall deiner Logik nach das Gefäßsystem als ein Rohr betrachtet (daher Verwendung der Kontinuitätsgleichung), in dem zweiten Fall jedoch als zwei unterschiedliche Rohre (daher Verwendung des Hagen-Poiseuille-Gesetz)?
Viele Grüße
Bruno |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 05. Nov 2020 20:45 Titel: Re: Rückfrage Nils Hoppenstedt Verfasst am: 05. Nov 2020 20:45 Titel: Re: Rückfrage |
 |
|
| Bruno-Baer hat Folgendes geschrieben: |
Wenn es um die Fließgeschwindigkeit des Blutes in der Aorta im Vergleich zu der Fließgeschwindigkeit in den Kapillaren geht, wird mit dem Kontinuitätsprinzip gerechnent. Aufgrund des viel größeren Gesamtquerschnitts von den Kapillaren ist daher die Blutgeschwindigkeit innerhalb der Kapillaren deutlich geringer. Da hier das Kontinuitätsgesetz verwendet wird, wird deiner Logik nach das Gefäßsystem als ein Rohr mit unterschiedlichen Querschnitten betrachtet.
|
Genau. Das Gefäßsystem wird als ein Rohr betrachtet und man vergleicht die relativen Fließgeschwindigkeit an der Stelle der Aorta mit einer Stelle im Bereich der Kapillaren.
| Bruno-Baer hat Folgendes geschrieben: |
Wenn es jedoch um Gefäßverengungen geht, wird dann aber mit dem Hagen-Poiseuille-Gesetz gerechnet. So heißt es dann beispielsweise, dass die Flussrate um 1/16 abnimmt, da sich der Gefäßradius halbiert. Doch warum wird hier auf einmal dieses Gesetzt verwendet und nicht die Kontinuitätsgleichung? Warum wird hier das Gefäß als zwei unterschiedliche Rohre betrachtet und daher das Hagen-Poiseuille-Gesetz verwendet?
|
Ja, hier werden zwei verschiedene Szenarien bzw. Gefäßsysteme verglichen:
Gefäß 1: das eines jungen, gesunden Menschen ohne Gefäßablagerungen
Gefäß 2: das einen (älteren) Menschen mit Gefäßablagerungen.
Man kann es auch so sagen: die Kontinuitätsgleichung wird benutzt, um die relative Änderung der Strömungsgeschwindigkeit entlang eines Rohres zu berechnen, während bei Hagen-Poiseuille eine Aussage über die absolute Durchflussmenge gemacht wird.
| Bruno-Baer hat Folgendes geschrieben: |
Es handelt sich doch trotzdem noch um ein Rohr, das jedoch an unterschiedlichen Stellen verschiedene Durchmesser hat.
|
Achtung: Im Modell von Hagen-Poiseuille wird davon ausgegangen, dass der Querschnitt entlang des Rohres konstant ist. Hat man es mit einem variierndem Querschnitt zu tun und man möchte die absolute Durchflussmenge bestimmen, wird es kompliziert und man kann Hagen-Poiseuille nicht verwenden (auch wenn die generelle Aussage, dass die Durchflussmenge empfindlich vom Durchmesser an der Verengung abhängt natürlich weiterhin richtig bleibt).
| Bruno-Baer hat Folgendes geschrieben: |
Aus irgendeinem Grund darf hier das Kontinuitätsgesetz nicht verwendet werden.
|
Natürlich darf man das. Dann erhält man die Aussage, dass das Blut im Bereich der Engstelle 4 mal so schnell fließt wie im weiten Bereich. Entscheidend für die Blutversorgung der Organe ist aber die absolute Durchflussmenge.
Viele Grüße,
Nils |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 05. Nov 2020 20:54 Titel: Mathefix Verfasst am: 05. Nov 2020 20:54 Titel: |
 |
|
Bei H-P wird die Viskosität des Fluids berücksichtigt: parabolisches Geschwindigkeitsprofil im Rohr. Unterstellt wird konstanter Durchmesser.
Bei der Konti-Glchg. wird eine Rohrleitung mit Querschnittsänderung betrachtet. Viskosität wird nicht berücksichtigt: Das Geschwindigkeitsprofil ist gleichmässig. Druckdifferenzen werden mit der Bernoulli-Strömungsgleichung bestimmt. |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 05. Nov 2020 21:06 Titel: Nils Hoppenstedt Verfasst am: 05. Nov 2020 21:06 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: |
Bei der Konti-Glchg. wird eine Rohrleitung mit Querschnittsänderung betrachtet. Viskosität wird nicht berücksichtigt: Das Geschwindigkeitsprofil ist gleichmässig. |
Präziser: Die Viskosität wird bei der Konti-Glchg nicht nicht berücksichtigt, sondern sie gilt unabhängig von der Viskosität.
Viele Grüße,
Nils |
|
 |
BrunoBaer
Anmeldungsdatum: 05.11.2020
Beiträge: 5
|
 BrunoBaer Verfasst am: 05. Nov 2020 22:39 Titel: Re: Rückfrage BrunoBaer Verfasst am: 05. Nov 2020 22:39 Titel: Re: Rückfrage |
 |
|
| Nils Hoppenstedt hat Folgendes geschrieben: | | Bruno-Baer hat Folgendes geschrieben: |
Wenn es um die Fließgeschwindigkeit des Blutes in der Aorta im Vergleich zu der Fließgeschwindigkeit in den Kapillaren geht, wird mit dem Kontinuitätsprinzip gerechnent. Aufgrund des viel größeren Gesamtquerschnitts von den Kapillaren ist daher die Blutgeschwindigkeit innerhalb der Kapillaren deutlich geringer. Da hier das Kontinuitätsgesetz verwendet wird, wird deiner Logik nach das Gefäßsystem als ein Rohr mit unterschiedlichen Querschnitten betrachtet.
|
Genau. Das Gefäßsystem wird als ein Rohr betrachtet und man vergleicht die relativen Fließgeschwindigkeit an der Stelle der Aorta mit einer Stelle im Bereich der Kapillaren.
| Bruno-Baer hat Folgendes geschrieben: |
Wenn es jedoch um Gefäßverengungen geht, wird dann aber mit dem Hagen-Poiseuille-Gesetz gerechnet. So heißt es dann beispielsweise, dass die Flussrate um 1/16 abnimmt, da sich der Gefäßradius halbiert. Doch warum wird hier auf einmal dieses Gesetzt verwendet und nicht die Kontinuitätsgleichung? Warum wird hier das Gefäß als zwei unterschiedliche Rohre betrachtet und daher das Hagen-Poiseuille-Gesetz verwendet?
|
Ja, hier werden zwei verschiedene Szenarien bzw. Gefäßsysteme verglichen:
Gefäß 1: das eines jungen, gesunden Menschen ohne Gefäßablagerungen
Gefäß 2: das einen (älteren) Menschen mit Gefäßablagerungen.
Man kann es auch so sagen: die Kontinuitätsgleichung wird benutzt, um die relative Änderung der Strömungsgeschwindigkeit entlang eines Rohres zu berechnen, während bei Hagen-Poiseuille eine Aussage über die absolute Durchflussmenge gemacht wird.
| Bruno-Baer hat Folgendes geschrieben: |
Es handelt sich doch trotzdem noch um ein Rohr, das jedoch an unterschiedlichen Stellen verschiedene Durchmesser hat.
|
Achtung: Im Modell von Hagen-Poiseuille wird davon ausgegangen, dass der Querschnitt entlang des Rohres konstant ist. Hat man es mit einem variierndem Querschnitt zu tun und man möchte die absolute Durchflussmenge bestimmen, wird es kompliziert und man kann Hagen-Poiseuille nicht verwenden (auch wenn die generelle Aussage, dass die Durchflussmenge empfindlich vom Durchmesser an der Verengung abhängt natürlich weiterhin richtig bleibt).
| Bruno-Baer hat Folgendes geschrieben: |
Aus irgendeinem Grund darf hier das Kontinuitätsgesetz nicht verwendet werden.
|
Natürlich darf man das. Dann erhält man die Aussage, dass das Blut im Bereich der Engstelle 4 mal so schnell fließt wie im weiten Bereich. Entscheidend für die Blutversorgung der Organe ist aber die absolute Durchflussmenge.
Viele Grüße,
Nils |
Guten Abend,
vielen Dank für die Antwort.
In der Engstelle eines verengten Gefäß (1/2 des ursprünglichen Radius) ist die Geschwindigkeit vier Mal größer als im weiten Abschnitt. Das ist die Aussage über die relative Geschwindigkeit. Wir reden über ein Gefäß mit unterschiedlichen Radien und vergleichen die Geschwindigkeiten miteinander.
Außerdem kann gesagt werden, dass ein Gefäß, das insgesamt um die Hälfe verengt ist, eine Durchflussrate von nur 1/16 der Durchflussrate eines gesunden Gefäßes hat. Wir vergleichen nun also zwei unterschiedliche Gefäße, nämlich ein gesundes und ein krankes.
Gehen wir nun von dem Fall aus, dass wir die Durchflussraten in einem Gefäß mit unterschiedlichen Gefäßradien bestimmen wollen. Das heißt also, dass es nur eine lokale Gefäßverengung gibt und keine globale Gefäßverengung gibt. Wie verändert sich dann die Durchflussrate im Gefäß im Vergleich zu einem gesunden Referenzgefäß? Es ist ja selten so, dass ein Gefäß über die ganze Länge vollkommen gleich verengt ist, sondern nur an bestimmten Stellen. Gehen wir von einem Gefäß aus, dass in der ersten Hälfte seiner Länge einen normalen Querschnitt besitzt und erst in seiner zweiten Hälfte um die Häfte verengt ist. Konkreter: Im ersten Abschnitt stimmt das Gefäß in seinem Durchmesser mit einem gesunden Vergleichsgefäß überein, in seinem zweiten Abschnitt ist es jedoch um die Hälfte verengt. Da wir nun ein Gefäß haben, dass unterschiedliche Radien besitzt, dürfte Hagen-Poiseuille nun nicht mehr greifen. Doch wie groß ist denn nun die Durchflussrate im Vergleich zum Referenzgefäß in diesem Gefäß? Ändert sich die Durchflussrate beim Übergang vom weiten in den engen Abschnitt (dürfte nicht der Fall sein, da laut des Kontinuitätsgesetzes die Durchflussrate konstant sein sollte)?
Ich bedanke mich noch einmal ausdrücklich für die bisherigen Antworten! Sie haben mir schon sehr weitergeholfen!
Viele Grüße
BrunoBaer |
|
 |
Klimafrosch
Anmeldungsdatum: 12.10.2020
Beiträge: 33
|
 Klimafrosch Verfasst am: 05. Nov 2020 22:57 Titel: Klimafrosch Verfasst am: 05. Nov 2020 22:57 Titel: |
 |
|
Das H-P-Gesetz gilt eigentlich nur für laminare Strömungen. Blut fließt aber in fast allen Gefäßen turbulent.
Wird der Radius halbiert, verringert sich die Durchflussfläche auf (1/2)^2 auf 0,25. Also fließt das Blut dann 1/0,25 = 4 mal so schnell. |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 05. Nov 2020 23:04 Titel: Re: Rückfrage Nils Hoppenstedt Verfasst am: 05. Nov 2020 23:04 Titel: Re: Rückfrage |
 |
|
| BrunoBaer hat Folgendes geschrieben: | | Gehen wir nun von dem Fall aus, dass wir die Durchflussraten in einem Gefäß mit unterschiedlichen Gefäßradien bestimmen wollen. Das heißt also, dass es nur eine lokale Gefäßverengung gibt und keine globale Gefäßverengung gibt. Wie verändert sich dann die Durchflussrate im Gefäß im Vergleich zu einem gesunden Referenzgefäß? |
Wie gesagt, das ist sehr kompliziert und hängt sehr von den Details der Engstelle ab. Eine einfache Formel gibt es dafür leider nicht.
Viele Grüße,
Nils |
|
 |
BrunoBaer
Anmeldungsdatum: 05.11.2020
Beiträge: 5
|
 BrunoBaer Verfasst am: 05. Nov 2020 23:10 Titel: Re: Rückfrage BrunoBaer Verfasst am: 05. Nov 2020 23:10 Titel: Re: Rückfrage |
 |
|
| Nils Hoppenstedt hat Folgendes geschrieben: | | BrunoBaer hat Folgendes geschrieben: | | Gehen wir nun von dem Fall aus, dass wir die Durchflussraten in einem Gefäß mit unterschiedlichen Gefäßradien bestimmen wollen. Das heißt also, dass es nur eine lokale Gefäßverengung gibt und keine globale Gefäßverengung gibt. Wie verändert sich dann die Durchflussrate im Gefäß im Vergleich zu einem gesunden Referenzgefäß? |
Wie gesagt, das ist sehr kompliziert und hängt sehr von den Details der Engstelle ab. Eine einfache Formel gibt es dafür leider nicht.
Viele Grüße,
Nils |
Vielen Dank für die Antwort! Das habe ich mir schon gedacht. Wahrscheinlich werden für solche Fragestellung bzw. komplexere wissenschaftliche und medizinische Anwendungen entsprechende Computerprogramme verwendet.
Ich bedanke mich ausdrücklich bei allen Usern, die mir geantwortet und geholfen haben. Insbesonder möchte ich Nils für die ausführlichen und klaren Antworten danken!
Viele Grüße
Bruno |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 05. Nov 2020 23:26 Titel: Nils Hoppenstedt Verfasst am: 05. Nov 2020 23:26 Titel: |
 |
|
Keine Ursache. Freut mich, wenn ich helfen konnte.
Viele Grüße,
Nils |
|
 |
Klimafrosch
Anmeldungsdatum: 12.10.2020
Beiträge: 33
|
 Klimafrosch Verfasst am: 06. Nov 2020 00:06 Titel: Klimafrosch Verfasst am: 06. Nov 2020 00:06 Titel: |
 |
|
>Doch wie groß ist denn nun die Durchflussrate im Vergleich zum Referenzgefäß in diesem Gefäß? Ändert sich die Durchflussrate beim Übergang vom weiten in den engen Abschnitt (dürfte nicht der Fall sein, da laut des Kontinuitätsgesetzes die Durchflussrate konstant sein sollte)?
Du betrachtest immer nur EIN Gefäß. Das wäre sehr leicht zu berechnen: Die Durchflussrate ist konstant, also ist die Fließgeschwindigkeit disproportional zur Fläche. Aber im menschlichen Körper gibt es zahlreiche Ausweichgefäße. Da muss man natürlich die Druckänderungen und Kompressibilität berücksichtigen, selbst wenn man für alle Gefäße turbulente Strömung ansetzt. |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 06. Nov 2020 00:38 Titel: Nils Hoppenstedt Verfasst am: 06. Nov 2020 00:38 Titel: |
 |
|
| Zitat: | | Die Durchflussrate ist konstant, also ist die Fließgeschwindigkeit disproportional zur Fläche. |
Ja klar, die Durchflussrate ist konstant, aber wenn ich Bruno richtig verstanden habe, geht es ihm darum, zu ermitteln, wie groß diese Durchflussrate konkret ist. Das dürfte dann nicht mehr so einfach zu berechnen sein.
-Nils |
|
 |
BrunoBaer1
Gast
|
 BrunoBaer1 Verfasst am: 06. Nov 2020 00:52 Titel: Re: Rückfrage BrunoBaer1 Verfasst am: 06. Nov 2020 00:52 Titel: Re: Rückfrage |
 |
|
| Klimafrosch hat Folgendes geschrieben: | >Doch wie groß ist denn nun die Durchflussrate im Vergleich zum Referenzgefäß in diesem Gefäß? Ändert sich die Durchflussrate beim Übergang vom weiten in den engen Abschnitt (dürfte nicht der Fall sein, da laut des Kontinuitätsgesetzes die Durchflussrate konstant sein sollte)?
Du betrachtest immer nur EIN Gefäß. Das wäre sehr leicht zu berechnen: Die Durchflussrate ist konstant, also ist die Fließgeschwindigkeit disproportional zur Fläche. Aber im menschlichen Körper gibt es zahlreiche Ausweichgefäße. Da muss man natürlich die Druckänderungen und Kompressibilität berücksichtigen, selbst wenn man für alle Gefäße turbulente Strömung ansetzt. |
Guten Morgen,
du beziehst dich nun aber auf den allerletzten Satz, richtig?
Denn in den Sätzen zuvor geht es mir um den Vergleich zwischen der Durchflussrate des Referenzgefäßes mit der Durchflussrate des Gefäßes, dessen eine Hälfte normal und die andere Hälfte z.B. um die Hälfte verengt ist. Beim Referenzgefäß kann mit Hagen-P. gearbeitet werden, da wir einen konstanten Durchmesser haben. Bei dem anderen Gefäß ändert sich jedoch der Durchmesser. Wenn die Prämisse, dass das Hagen-Poiseuille nur für ein Gefäß mit konstantem Durchmesser verwendet werden darf, stimmt, dann können wir es in diesem Fall nicht anwenden. Anscheindend ist es in diesem Fall nicht so einfach zu berechnen (siehe vorherige Antworten). Ist doch richtig, oder?
Ich bin mir nicht ganz sicher, was du mit Ausweichgefäßen meinst. Was sind Ausweichgefäße und welche Bedeutung haben sie auf die Durchflussrate und/oder Geschwindigkeit? Könntest du in diesem Zusammenhang auch noch einmal genau erklären, welche Rolle Druckänderung, Kompressibiltät (des Blutes??) und turbulente Strömung spielen? Die Zusammenhänge sind mir nicht ganz klar.
Viele Grüße
Bruno |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 06. Nov 2020 09:51 Titel: Re: Rückfrage DrStupid Verfasst am: 06. Nov 2020 09:51 Titel: Re: Rückfrage |
 |
|
| BrunoBaer1 hat Folgendes geschrieben: | | Wenn die Prämisse, dass das Hagen-Poiseuille nur für ein Gefäß mit konstantem Durchmesser verwendet werden darf, stimmt, dann können wir es in diesem Fall nicht anwenden. |
Man kann Hagen-Poiseuille für jeden Abschnitt mit konstantem Querschnitt verwenden. Zusammen mit der Kontinuitätsbedingung liefert das die Durchflussrate für das gesamte Gefäß. |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 06. Nov 2020 10:24 Titel: Mathefix Verfasst am: 06. Nov 2020 10:24 Titel: |
 |
|
Ich fasse mal zusammen
1. Hagen-Poiseuille Gleichungen
Strömungsgeschwindigkeit
 = v_0 -\frac{\Delta p }{4\cdot \eta \cdot l } \cdot r^{2} )
Maximalgeschwindigkeit

Mittlere Geschwindigkeit

Volumenstrom
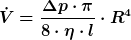
Voraussetzungen
- Stationäre Strömung
- Laminare Strömung
- Inkompressibles Fluid
- Konstanter Radius
- Newton'sches Fluid: Trifft nicht auf Blut zu.
2. Kontinuitätsgleichung und Bernoulli'sche Strömungsgleichung
Bernoulli Druckgleichung
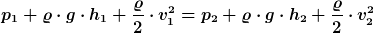
Voraussetzung
Viskositätsfreiheit
In der erweiterten Bernoulligleichung können turbulente und instationäre Strömungen, kompressible Fluide, Rohrreibung ... berücksichtigt werden
Kontinuitätsgleichung
Variabler Radius

Zuletzt bearbeitet von Mathefix am 19. Nov 2020 11:33, insgesamt einmal bearbeitet |
|
 |
Bruno1
Gast
|
 Bruno1 Verfasst am: 06. Nov 2020 11:05 Titel: Re: Rückfrage Bruno1 Verfasst am: 06. Nov 2020 11:05 Titel: Re: Rückfrage |
 |
|
| DrStupid hat Folgendes geschrieben: | | BrunoBaer1 hat Folgendes geschrieben: | | Wenn die Prämisse, dass das Hagen-Poiseuille nur für ein Gefäß mit konstantem Durchmesser verwendet werden darf, stimmt, dann können wir es in diesem Fall nicht anwenden. |
Man kann Hagen-Poiseuille für jeden Abschnitt mit konstantem Querschnitt verwenden. Zusammen mit der Kontinuitätsbedingung liefert das die Durchflussrate für das gesamte Gefäß. |
Das heißt, meine Prämisse ist falsch? Kann jemand vielleicht ein Beispiel mit konkreten Werten durchrechen? Das heißt also, die Durchflussrate eines gesunden Gefäßes mit einem bestimmten Radius (sagen wir mal r=2cm) und die Durchflussrate eines Gefäßes mit zunächst gesundem Radius (entspricht dem Referenzgefäß, also r=2cm) und dann zur Hälfte verengtem Radius(also r1 cm?
Wir sprechen gerade sehr abstrakt über das Thema. Ich denke, ein konkretes Beispiel würde extrem helfen!
Vielen Dank Euch allen für Eure Mühe!
Liebe Grüße
Bruno |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 06. Nov 2020 11:51 Titel: Re: Rückfrage Mathefix Verfasst am: 06. Nov 2020 11:51 Titel: Re: Rückfrage |
 |
|
| Bruno1 hat Folgendes geschrieben: |
Das heißt, meine Prämisse ist falsch? Kann jemand vielleicht ein Beispiel mit konkreten Werten durchrechen? Das heißt also, die Durchflussrate eines gesunden Gefäßes mit einem bestimmten Radius (sagen wir mal r=2cm) und die Durchflussrate eines Gefäßes mit zunächst gesundem Radius (entspricht dem Referenzgefäß, also r=2cm) und dann zur Hälfte verengtem Radius(also r1 cm?
Wir sprechen gerade sehr abstrakt über das Thema. Ich denke, ein konkretes Beispiel würde extrem helfen!
Vielen Dank Euch allen für Eure Mühe!
Liebe Grüße
Bruno |
Ich habe Dir doch die Formel für die Durchflussrate = Volumenstrom = 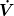 hingeschrieben. hingeschrieben.
Die Verknüpfung mit der Kontinuitätsgleichung ist

Was reinfliesst muss auch rausfliessen.
Du solltest in der Lage sein die Durchlussraten bei 2 verschiedenen Radien numerisch zu berechnen.
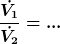 |
|
 |
Bruno1
Gast
|
 Bruno1 Verfasst am: 06. Nov 2020 12:07 Titel: Re: Rückfrage Bruno1 Verfasst am: 06. Nov 2020 12:07 Titel: Re: Rückfrage |
 |
|
| Mathefix hat Folgendes geschrieben: | | Bruno1 hat Folgendes geschrieben: |
Das heißt, meine Prämisse ist falsch? Kann jemand vielleicht ein Beispiel mit konkreten Werten durchrechen? Das heißt also, die Durchflussrate eines gesunden Gefäßes mit einem bestimmten Radius (sagen wir mal r=2cm) und die Durchflussrate eines Gefäßes mit zunächst gesundem Radius (entspricht dem Referenzgefäß, also r=2cm) und dann zur Hälfte verengtem Radius(also r1 cm?
Wir sprechen gerade sehr abstrakt über das Thema. Ich denke, ein konkretes Beispiel würde extrem helfen!
Vielen Dank Euch allen für Eure Mühe!
Liebe Grüße
Bruno |
Ich habe Dir doch die Formel für die Durchflussrate = Volumenstrom = 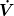 hingeschrieben. hingeschrieben.
Die Verknüpfung mit der Kontinuitätsgleichung ist

Was reinfliesst muss auch rausfliessen.
Du solltest in der Lage sein die Durchlussraten bei 2 verschiedenen Radien numerisch zu berechnen.
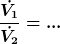 |
Guten Tag,
vielen Dank für die Antwort. Die Geschwindigkeit errechne ich mit der H.-P.-Gleichung, oder?
Viele Grüße
Bruno |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 06. Nov 2020 12:10 Titel: Re: Rückfrage DrStupid Verfasst am: 06. Nov 2020 12:10 Titel: Re: Rückfrage |
 |
|
| Bruno1 hat Folgendes geschrieben: | | Kann jemand vielleicht ein Beispiel mit konkreten Werten durchrechen? |
Angenommen das Gefäß hat n Abschnitte mit den Längen 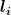 und den Radien und den Radien 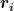 , dann gilt für diese Abschnitte nach Hagen-Poiseuille , dann gilt für diese Abschnitte nach Hagen-Poiseuille
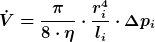
wobei der Volumenstrom 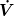 gemäß Kontinuitätsbedingung für inkompressible Medien in allen Abschnitten gleich sein muss. Außerdem müssen sich die Druckabfälle gemäß Kontinuitätsbedingung für inkompressible Medien in allen Abschnitten gleich sein muss. Außerdem müssen sich die Druckabfälle 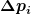 der einzelnen Abschnitte zum gesamten Druckabfall über das komplette Gefäß addieren: der einzelnen Abschnitte zum gesamten Druckabfall über das komplette Gefäß addieren:

Das ergibt ein lineares Gleichungssystem mit n+1 Gleichungen (n x Hagen-Poiseuille + Druckabfall) und n+1 Unbekannten (n Druckabfälle + Volumenstrom).
Im Fall von zwei Abschnitten führt die Lösung dieses Gleichungssystems zum Volumenstrom

Da kannst Du jetzt konkrete Werte einsetzen. |
|
 |
BrunoBaer
Anmeldungsdatum: 05.11.2020
Beiträge: 5
|
 BrunoBaer Verfasst am: 06. Nov 2020 12:31 Titel: Re: Rückfrage BrunoBaer Verfasst am: 06. Nov 2020 12:31 Titel: Re: Rückfrage |
 |
|
| DrStupid hat Folgendes geschrieben: | | Bruno1 hat Folgendes geschrieben: | | Kann jemand vielleicht ein Beispiel mit konkreten Werten durchrechen? |
Angenommen das Gefäß hat n Abschnitte mit den Längen 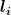 und den Radien und den Radien 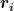 , dann gilt für diese Abschnitte nach Hagen-Poiseuille , dann gilt für diese Abschnitte nach Hagen-Poiseuille
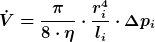
wobei der Volumenstrom 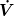 gemäß Kontinuitätsbedingung für inkompressible Medien in allen Abschnitten gleich sein muss. Außerdem müssen sich die Druckabfälle gemäß Kontinuitätsbedingung für inkompressible Medien in allen Abschnitten gleich sein muss. Außerdem müssen sich die Druckabfälle 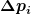 der einzelnen Abschnitte zum gesamten Druckabfall über das komplette Gefäß addieren: der einzelnen Abschnitte zum gesamten Druckabfall über das komplette Gefäß addieren:

Das ergibt ein lineares Gleichungssystem mit n+1 Gleichungen (n x Hagen-Poiseuille + Druckabfall) und n+1 Unbekannten (n Druckabfälle + Volumenstrom).
Im Fall von zwei Abschnitten führt die Lösung dieses Gleichungssystems zum Volumenstrom

Da kannst Du jetzt konkrete Werte einsetzen. |
Leider kann ich das Foto (die Datei) nicht öffnen. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 06. Nov 2020 12:36 Titel: Re: Rückfrage DrStupid Verfasst am: 06. Nov 2020 12:36 Titel: Re: Rückfrage |
 |
|
| BrunoBaer hat Folgendes geschrieben: | | Leider kann ich das Foto (die Datei) nicht öffnen. |
Da gibt es keine Fotos oder Dateien. |
|
 |
BrunoBaer
Anmeldungsdatum: 05.11.2020
Beiträge: 5
|
 BrunoBaer Verfasst am: 06. Nov 2020 13:44 Titel: Re: Rückfrage BrunoBaer Verfasst am: 06. Nov 2020 13:44 Titel: Re: Rückfrage |
 |
|
| DrStupid hat Folgendes geschrieben: | | Bruno1 hat Folgendes geschrieben: | | Kann jemand vielleicht ein Beispiel mit konkreten Werten durchrechen? |
Angenommen das Gefäß hat n Abschnitte mit den Längen 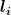 und den Radien und den Radien 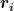 , dann gilt für diese Abschnitte nach Hagen-Poiseuille , dann gilt für diese Abschnitte nach Hagen-Poiseuille
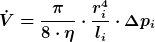
wobei der Volumenstrom 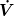 gemäß Kontinuitätsbedingung für inkompressible Medien in allen Abschnitten gleich sein muss. Außerdem müssen sich die Druckabfälle gemäß Kontinuitätsbedingung für inkompressible Medien in allen Abschnitten gleich sein muss. Außerdem müssen sich die Druckabfälle 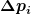 der einzelnen Abschnitte zum gesamten Druckabfall über das komplette Gefäß addieren: der einzelnen Abschnitte zum gesamten Druckabfall über das komplette Gefäß addieren:

Das ergibt ein lineares Gleichungssystem mit n+1 Gleichungen (n x Hagen-Poiseuille + Druckabfall) und n+1 Unbekannten (n Druckabfälle + Volumenstrom).
Im Fall von zwei Abschnitten führt die Lösung dieses Gleichungssystems zum Volumenstrom

Da kannst Du jetzt konkrete Werte einsetzen. |
Guten Tag,
ich bedanke mich für die Hilfe.
Das heißt also, dass es einen Volumenstrom in dem Gefäß gibt, der in beiden Abschnitten gleich groß ist. Der Volumenstrom wird also in dem Gefäß mit den beiden verschiedenen Abschnitten (einem normalen Abschnitt + einen verengten Abschnitt) kleiner sein als in dem Referenzgefäß. Ist das so weit korrekt?
Rein konzeptionell verstehe ich jedoch nicht, warum der Volumenstrom in dem Abschnitt vor der Verengung auch schon geringer ist. Hier besteht zu dem Referenzgefäß ja noch gar kein Unterschied und erst am Beginn der Verengung gibt es einen Unterschied zu diesem Referenzgefäß. Also wirkt sich die die Verengung "downstream" auf den Volumenstrom "upstream" aus. Doch warum ist das so? Kann mir das jemand rein konzeptionell (ohne viel Formeln) erklären?
Viele Grüße
Bruno |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 06. Nov 2020 14:03 Titel: Re: Rückfrage Nils Hoppenstedt Verfasst am: 06. Nov 2020 14:03 Titel: Re: Rückfrage |
 |
|
| BrunoBaer hat Folgendes geschrieben: |
Das heißt also, dass es einen Volumenstrom in dem Gefäß gibt, der in beiden Abschnitten gleich groß ist. Der Volumenstrom wird also in dem Gefäß mit den beiden verschiedenen Abschnitten (einem normalen Abschnitt + einen verengten Abschnitt) kleiner sein als in dem Referenzgefäß. Ist das so weit korrekt?
|
Ja , das ist korrekt. Der Volumenstrom muss ja in allen Abschnitten gleich groß sein. Das ist ja gerade die Aussage der Kontinuitätsgleichung: In jedem Volumenelement muss pro Zeiteinheit genau so viel hineinfließen wie auch heraus fließt. Und natürlich ist der Volumenstrom auch kleiner als in einem Referenzgefäß ohne Verengung.
| BrunoBaer hat Folgendes geschrieben: |
Rein konzeptionell verstehe ich jedoch nicht, warum der Volumenstrom in dem Abschnitt vor der Verengung auch schon geringer ist. Hier besteht zu dem Referenzgefäß ja noch gar kein Unterschied und erst am Beginn der Verengung gibt es einen Unterschied zu diesem Referenzgefäß. Also wirkt sich die die Verengung "downstream" auf den Volumenstrom "upstream" aus. Doch warum ist das so? Kann mir das jemand rein konzeptionell (ohne viel Formeln) erklären?
|
Ganz ohne Formel: In der Engstelle geht es halt langsamer vorwärts und das staut sich sozusagen in den weiten Abschnitt zurück. Das ist wie auf der Autobahn: wenn es irgendwo einspurig wird, stockt der Verkehr auch viele Kilometer vor der Engstelle.
Viele Grüße,
Nils
P.S.: wenn du Probleme mit dem Anzeigen von Formeln hast, versuche die Seite mal in einem anderen Browser zu öffnen. |
|
 |
VeryApe

Anmeldungsdatum: 10.02.2008
Beiträge: 3271
|
 VeryApe Verfasst am: 06. Nov 2020 14:48 Titel: VeryApe Verfasst am: 06. Nov 2020 14:48 Titel: |
 |
|
| Zitat: | | rein konzeptionell verstehe ich jedoch nicht, warum der Volumenstrom in dem Abschnitt vor der Verengung auch schon geringer ist. Hier besteht zu dem Referenzgefäß ja noch gar kein Unterschied und erst am Beginn der Verengung gibt es einen Unterschied zu diesem Referenzgefäß. |
Das wäre im Prinzip so also würde man einen Einkaufswagen anschieben, der wieder einen anderen Einkaufswagen anschiebt, im Vergleich zu man schiebt einen Einkaufswagen an der aber leider hinten am Auto ansteht und das ganze Auto mit angeschoben wird, und man wundert sich darüber warum nichts weitergeht.
Die Pumpe muß gegen all diese Druckdifferenzen anarbeiten. Druckdifferenzen aufgrund Schwerkraft, Druckdifferenzen aufgrund Beschleunigung, Druckdifferenzen aufgrund Reibung.
_________________
WAS IST LOS IN EUROPA? https://www.youtube.com/watch?v=a9mduhSSC5w |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 17. Nov 2020 12:59 Titel: Re: Rückfrage Mathefix Verfasst am: 17. Nov 2020 12:59 Titel: Re: Rückfrage |
 |
|
| DrStupid hat Folgendes geschrieben: |
Im Fall von zwei Abschnitten führt die Lösung dieses Gleichungssystems zum Volumenstrom
 |
Stelle folgende Überlegung zur Diskussion:
Ein Rohr bestehe aus zwei Abschnitten jeweils der Länge l = 1 und den Radien r_1 und r_2
Dann gilt ceteris paribus

Das Verhältnis der Radien sei
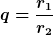
Damit gilt
 } )
Der Radius r_2 sei konstant, variiert wird r_1
Fall 1: r_1 = r_2
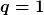
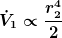
Fall 2: r_1 < r_2
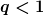
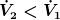
Fall 3: r_1 > r_2
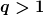
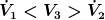
Frage
Wie erklärt sich
a) der Widerspruch, dass im Fall 3 der Volumenstrom grösser ist als im Rohr mit konstantem Querschnitt.
b) in den Fällen 2 und 3 der Volumenstrom von der Reihenfolge der Querschnittsänderung bzw. Strömungsrichtung des Fluids abhängt.
Ist meine Überlegung abwegig oder ist H-P bei Rohren mit nicht konstantem Querschnitt nicht anwendbar?
Zuletzt bearbeitet von Mathefix am 17. Nov 2020 13:23, insgesamt einmal bearbeitet |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 17. Nov 2020 13:22 Titel: Re: Rückfrage Myon Verfasst am: 17. Nov 2020 13:22 Titel: Re: Rückfrage |
 |
|
| Mathefix hat Folgendes geschrieben: | Wie erklärt sich
a) der Widerspruch, dass im Fall 3 der Volumenstrom grösser ist als im Rohr mit konstantem Querschnitt. |
Auf die Schnelle kann sehe ich da keinen Widerspruch(?). In Fall 3 ist r1 grösser als in Fall 1, also sollte da auch der Volumenstrom grösser sein. Ein allfälliger Widerstand beim Übergang zum kleineren Radius ist da natürlich nicht berücksichtigt.
| Zitat: | | b) in den Fällen 2 und 3 der Volumenstrom von der Reihenfolge der Querschnittsänderung bzw. Strömungsrichtung des Fluids abhängt. |
Das kann man aus DrStupids Gleichung nicht folgern. Wenn Du die Reihenfolge änderst, also r1‘=r2, r2‘=r1, dann würde auch der Zähler in der Proportionalität
| Zitat: |  } ) |
ändern. |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 18. Nov 2020 13:09 Titel: Re: Rückfrage Mathefix Verfasst am: 18. Nov 2020 13:09 Titel: Re: Rückfrage |
 |
|
| Myon hat Folgendes geschrieben: |
| Zitat: | | b) in den Fällen 2 und 3 der Volumenstrom von der Reihenfolge der Querschnittsänderung bzw. Strömungsrichtung des Fluids abhängt. |
Das kann man aus DrStupids Gleichung nicht folgern. Wenn Du die Reihenfolge änderst, also r1‘=r2, r2‘=r1, dann würde auch der Zähler in der Proportionalität
| Zitat: |  } ) |
ändern. |
@Myon
Dein Einwand trifft zu; habe mich verrechnet. |
|
 |
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5168
|
 DrStupid Verfasst am: 18. Nov 2020 14:43 Titel: Re: Rückfrage DrStupid Verfasst am: 18. Nov 2020 14:43 Titel: Re: Rückfrage |
 |
|
Die Lösung für den allgemeinen Fall mit n unterschiedlichen Radien (und ohne Berücksichtung der Übergänge) ist übrigens
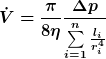
und ich frage mich gerade, ob man aus der Summe einfach ein Integral machen kann, um den Volumenstrom durch ein Gefäß mit kontinuierlicher Änderung des Radius zu berechnen:
^4 }}} }}) |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 18. Nov 2020 17:58 Titel: Re: Rückfrage Mathefix Verfasst am: 18. Nov 2020 17:58 Titel: Re: Rückfrage |
 |
|
| DrStupid hat Folgendes geschrieben: | Die Lösung für den allgemeinen Fall mit n unterschiedlichen Radien (und ohne Berücksichtung der Übergänge) ist übrigens
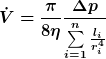
und ich frage mich gerade, ob man aus der Summe einfach ein Integral machen kann, um den Volumenstrom durch ein Gefäß mit kontinuierlicher Änderung des Radius zu berechnen:
^4 }}} }}) |
@ DrStupid
Ich bin der Meinung, dass HP bei veränderlichem Querschnitt grundsätzlich nicht angewendet werden kann:
1. In der Herleitung der HP-Gleichung wird von einer konstanten Strömungsgeschwindigkeit längs eines Stromfadens (stationäre Strömung) ausgegangen.
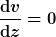 ; ; 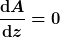
Unter Beachtung der Kontinuitätsgleichung folgt daraus ein konstanter Rohrdurchmesser. Dem entspricht die Aufgabe nicht.
2. Der Ansatz Gesamtdruck gleich der Summe der Partialdrücke
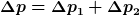
bedeutet bei dieser Aufgabe
p_1 = Druck am Anfang von Rohrelement 1
p_2 = Druck am Ende von Rohrelement 1
p_3 = Druck am Anfang von Rohrelement 2
p_4 = Druck am Ende von Rohrelement 2
 + (p_3 - p_4))
Die Glchg. ist nur erfüllt, wenn an der Stelle der Querschnittsänderung gilt
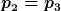
Da sich an der Stelle der Querschnittsänderung die Strömungsgeschwindigkeit(Kontinuitätsgleichung) und damit der Druck (Bernoulli) ändert, ist
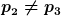 da da 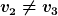
Diese Druckänderung wird in der zweifachen Anwendung von HP nicht berücksichtigt.
Bei einem Rohr mit veränderlichen Radius (Diffusor) ist nicht nur r = r(z) sondern auch die Reibungsfläche O = O(r(z), z) und damit ist v = v(r,z).
Da v_z nicht konstant ist, kann HP nicht angewendet werden.
Mein Vorschlag:
Bernoulli-Gleichung mit Erweiterung der inneren Reibungsarbeit. |
|
 |
|















