| Autor |
Nachricht |
Philip1630
Anmeldungsdatum: 27.07.2020
Beiträge: 11
|
 Philip1630 Verfasst am: 27. Jul 2020 13:55 Titel: Bungeespringer Funktion in Abhängigkeit des Weges statt Zeit Philip1630 Verfasst am: 27. Jul 2020 13:55 Titel: Bungeespringer Funktion in Abhängigkeit des Weges statt Zeit |
 |
|
Hallo liebe Community,
bin Philip, neu hier und komme einfach auf keine Lösung.
Folgendes Aufgabe:
Es geht um einen Bungeespringer, der als Massepunkt (m) vor dem Absprung betrachtet wird. Die Ausgangslage beträgt l.
Masse des Seils und Luftwiderstand bleiben unberücksichtigt. Nehmen Sie an, dass die Masse nicht nach oben abspringt, sondern lediglich fallen gelassen wird.
x(1Punkt), also die Geschwindigkeit ist positiv in Richtung g gekennzeichnet.
1.1. Stellen Sie die Beschleunigungsfunktion x(2 Punkt) also die Beschleunigung des Massepunkts in Abhängigkeit des Weges x1 auf. Vernachlässigen Sie dabei die Kraft aufgrund der Dehnung des Seils. X(2Punkt) (X1)
Als Lösung habe ich da: = 1/2 (V0^2+2g)^-1/2. Dabei komme ich aber nicht auf den Weg
1.2. Welche Zeit benötigt der Massepunkt bis er vollständig gespannt ist?
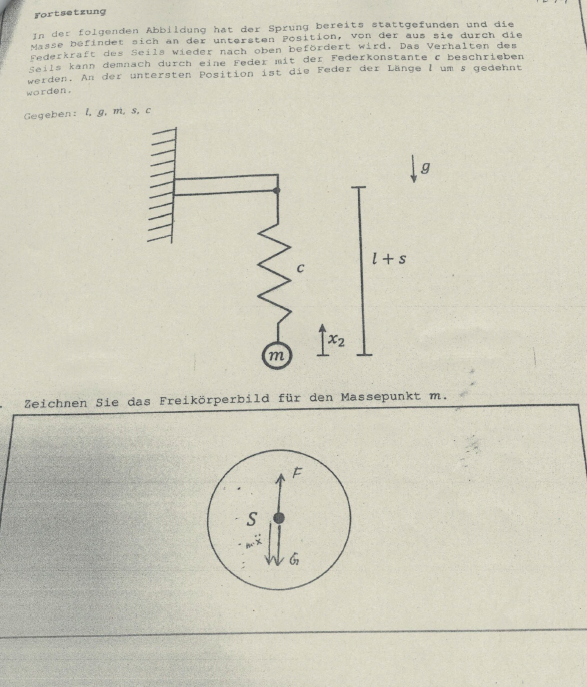
1.3.Dabei geht es um die Aufwärtsbewegung, die als Federsystem mit der Federkonstante C und dem Weg x2 und der Wegstrecke l+s betrachtet wird.
Stellen Sie die Beschleunigungsfunktion x(2Punkt) des Massepunkts in Abhängigkeit des Wegs X2 auf. Die Funktion soll für den Bereich 0<X2<=s gelten.
1.4. Welche Geschwindigkeit X2(1Punkt) besitzt der Massepunkt, wenn die Dehnung des Seils wieder den Wert 0 erreicht?
Leider habe ich keine Musterlösung der Aufgabe und komme nicht auf eine Lösung, da ich in den Unterlagen oder im Netz bei vergleichbaren Aufgaben immer die Funktion in Abhängigkeit zur Zeit und nicht zum Weg betrachtet wird.
Über einen Lösungsansatz oder Lösung würde ich mich echt freuen.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 27. Jul 2020 14:33 Titel: Mathefix Verfasst am: 27. Jul 2020 14:33 Titel: |
 |
|
Verstehe die Aufgabe nicht.
zu 1.1 Geht es hier um den freien Fall? Dann ist die Beschleunigung "g" unabhängig vom Weg.
|
|
 |
Philip1630
Anmeldungsdatum: 27.07.2020
Beiträge: 11
|
 Philip1630 Verfasst am: 27. Jul 2020 15:02 Titel: Philip1630 Verfasst am: 27. Jul 2020 15:02 Titel: |
 |
|
@mathefix: Im ersten Teil schon um den freien Fall. Im zweiten dann um die Aufwärtsbewegung. Jedoch geht es ja nicht um die Beschleunigung sondern um die Funktion a(x), also der Funktion des freien Falles in Abhängigkeit zum Weg. Finde sonst nur a(t), also in Abhängigkeit zur Zeit.
Ist eine Altklausur. Daher habe ich leider keine Lösung bzw nur die von einem Kommilitonen wo ich nicht weiß, ob die richtig ist und wie man darauf kommt.
a(x)=1/2 (v0^2+2g)^-1/2
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 27. Jul 2020 15:18 Titel: Mathefix Verfasst am: 27. Jul 2020 15:18 Titel: |
 |
|
| Philip1630 hat Folgendes geschrieben: | @mathefix: Im ersten Teil schon um den freien Fall. Im zweiten dann um die Aufwärtsbewegung. Jedoch geht es ja nicht um die Beschleunigung sondern um die Funktion a(x), also der Funktion des freien Falles in Abhängigkeit zum Weg. Finde sonst nur a(t), also in Abhängigkeit zur Zeit.
Ist eine Altklausur. Daher habe ich leider keine Lösung bzw nur die von einem Kommilitonen wo ich nicht weiß, ob die richtig ist und wie man darauf kommt.
a(x)=1/2 (v0^2+2g)^-1/2 |
Wie schon gesagt, beim freien Fall ist die Beschleunigung g unabhäng vom Weg: a(x) = g = const.
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 27. Jul 2020 18:19 Titel: Mathefix Verfasst am: 27. Jul 2020 18:19 Titel: |
 |
|
|
Für was steht denn a?
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 27. Jul 2020 18:38 Titel: Nils Hoppenstedt Verfasst am: 27. Jul 2020 18:38 Titel: |
 |
|
@ Philip: Finde ich cool, dass du nicht einfach die komplette Aufgabe einstellst, woraus klar ersichtlich ist, worum es in "Teil 1" und "Teil 2" geht oder was die Abkürzungen bedeuten sollen (von einer Skizze ganz zu schweigen). So bleibt die Aufgabenstellung schön mysteriös und man hat was zum Knobeln.... 
|
|
 |
Philip1630
Anmeldungsdatum: 27.07.2020
Beiträge: 11
|
 Philip1630 Verfasst am: 27. Jul 2020 22:14 Titel: Philip1630 Verfasst am: 27. Jul 2020 22:14 Titel: |
 |
|
@Mathefix: a ist die Beschleunigung, also X(2Punkt) bzw die Geschwindigkeitsveränderung über den Zeitraum oder dV/dt.
Nur die Gravitation g kommt mir halt zu einfach vor und die Lösung von meinem Kommilitonen irritiert mich.
@Nils: Hier die Aufgabenstellung. Konnte vorher noch keine Bilder hochladen[/img]
| Beschreibung: |
|
| Dateigröße: |
578.92 KB |
| Angeschaut: |
2084 mal |

|
| Beschreibung: |
|

Download |
| Dateiname: |
bungee3.PNG |
| Dateigröße: |
288.2 KB |
| Heruntergeladen: |
164 mal |
|
|
 |
Philip1630
Anmeldungsdatum: 27.07.2020
Beiträge: 11
|
 Philip1630 Verfasst am: 27. Jul 2020 22:15 Titel: Philip1630 Verfasst am: 27. Jul 2020 22:15 Titel: |
 |
|
Seite2
| Beschreibung: |
|
| Dateigröße: |
639.07 KB |
| Angeschaut: |
2082 mal |
|
|
|
 |
Philip1630
Anmeldungsdatum: 27.07.2020
Beiträge: 11
|
 Philip1630 Verfasst am: 27. Jul 2020 22:15 Titel: Philip1630 Verfasst am: 27. Jul 2020 22:15 Titel: |
 |
|
Seite3
| Beschreibung: |
|

Download |
| Dateiname: |
bungee3.PNG |
| Dateigröße: |
288.2 KB |
| Heruntergeladen: |
190 mal |
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 28. Jul 2020 12:36 Titel: Mathefix Verfasst am: 28. Jul 2020 12:36 Titel: |
 |
|
Die Lösung Deines Kommilitonen ist falsch!
Bewegungsgleichungen
 x = v_0 \cdot t + \frac{1}{2}\cdot g\cdot t^{2})
 \dot{x} = v_0 + g\cdot t )
aus ( 1)
^{2} +\frac{2\cdot x}{g} } )
Einsetzen in (2) ergibt

^{-\frac{1}{2} } \cdot g \cdot \dot{x})
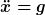
qed
Zuletzt bearbeitet von Mathefix am 28. Jul 2020 13:46, insgesamt 3-mal bearbeitet |
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 28. Jul 2020 13:22 Titel: Nils Hoppenstedt Verfasst am: 28. Jul 2020 13:22 Titel: |
 |
|
Ich komme auf folgende Lösung:
Beschleunigung für freien Fall:

Zeit bis zum Spannen des Seils:

Beschleunigung für Auwärtsbewegung:
 - g )
Die Geschwindigkeit an der Stelle, an der das Seil wieder die Dehnung Null hat, folgt aus der Energieerhaltung:

Und dann nach  auflösen. auflösen.
Viele Grüße,
Nils
Zuletzt bearbeitet von Nils Hoppenstedt am 28. Jul 2020 13:32, insgesamt 3-mal bearbeitet |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 28. Jul 2020 13:23 Titel: Myon Verfasst am: 28. Jul 2020 13:23 Titel: |
 |
|
| Mathefix hat Folgendes geschrieben: | ^{-\frac{1}{2} } \cdot g ) |
Du hast doch oben bereits richtig geschrieben, dass ohne Einfluss des Seils  gilt, weshalb schreibst Du nun etwas anderes (die Beschleunigung ist die zeitliche Ableitung der Geschwindigkeit)? gilt, weshalb schreibst Du nun etwas anderes (die Beschleunigung ist die zeitliche Ableitung der Geschwindigkeit)?
PS: Den Beitrag von Nils erst später gesehen...
PPS @Nils: Ich denke, die Geschwindigkeit nach Entspannung des Seils kann auch einfach in Abhängigkeit von l angegeben werden. Dies unter der Voraussetzung, dass mit „Dehnung=0“ nicht die neue Gleichgewichtslage mit Masse nach Ausschwingen gemeint ist.
Zuletzt bearbeitet von Myon am 28. Jul 2020 13:48, insgesamt einmal bearbeitet |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 28. Jul 2020 13:45 Titel: Mathefix Verfasst am: 28. Jul 2020 13:45 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | Mathefix hat Folgendes geschrieben: | ^{-\frac{1}{2} } \cdot g ) |
Du hast doch oben bereits richtig geschrieben, dass ohne Einfluss des Seils  gilt, weshalb schreibst Du nun etwas anderes (die Beschleunigung ist die zeitliche Ableitung der Geschwindigkeit)? gilt, weshalb schreibst Du nun etwas anderes (die Beschleunigung ist die zeitliche Ableitung der Geschwindigkeit)?
|
@Myon
Du hast mich überholt. Ich war noch im Editiermodus, musste zwischendurch kurz weg.
Schau Dir jetzt meine endgültige Lösung an.
|
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 28. Jul 2020 14:13 Titel: Myon Verfasst am: 28. Jul 2020 14:13 Titel: |
 |
|
@Mathefix: Naja, aus Deiner Gleichung für ) folgt doch unmittelbar folgt doch unmittelbar  , da gibt es eigentlich nichts zu beweisen... , da gibt es eigentlich nichts zu beweisen...
|
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 28. Jul 2020 14:16 Titel: Mathefix Verfasst am: 28. Jul 2020 14:16 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | @Mathefix: Naja, aus Deiner Gleichung für ) folgt doch unmittelbar folgt doch unmittelbar  , da gibt es eigentlich nichts zu beweisen... , da gibt es eigentlich nichts zu beweisen... |
Mit war das von vorneherein klar. s. Meinen ersten Kommentar.
Ich wollte nur den Rechengang des Kommilitonen nachvollziehen.
|
|
 |
Philip1630
Anmeldungsdatum: 27.07.2020
Beiträge: 11
|
 Philip1630 Verfasst am: 28. Jul 2020 16:24 Titel: Philip1630 Verfasst am: 28. Jul 2020 16:24 Titel: |
 |
|
Ok, super vielen lieben Dank schon mal.
So weit einleuchtend, da g ja eine gleichmäßige Beschleunigung ist und nur diese in der Abwärtsbewegung betrachtet wird.
Eine Sache nur: Ihr schreibt ja aus x von t geht das heraus.
Genau das ist das was mich bei dieser Aufgabe verunsichert. Da steht ja im Lösungsfeld X zwei Punkt (Beschleunigung) von X1, also dem Weg und nicht von der Zeit. Ist das egal?
Die Aufgabe findet man ja häufig wieder, aber immer nur mit der Funktion nach der Zeit und nicht nach dem Weg.
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 28. Jul 2020 18:01 Titel: Nils Hoppenstedt Verfasst am: 28. Jul 2020 18:01 Titel: |
 |
|
| Philip1630 hat Folgendes geschrieben: |
Eine Sache nur: Ihr schreibt ja aus x von t geht das heraus.
Genau das ist das was mich bei dieser Aufgabe verunsichert. Da steht ja im Lösungsfeld X zwei Punkt (Beschleunigung) von X1, also dem Weg und nicht von der Zeit. Ist das egal? |
Vergiss was im Lösungsfeld steht, das ist Quark. Es ist einfach  . Keine Ahnung was deinen Kommilitonen hier geritten hat... . Keine Ahnung was deinen Kommilitonen hier geritten hat...
Die Beschleunigung ist grundsätzlich definiert als 2. Ableitung des Ortes nach der Zeit. Diese Größe kann man nun ausdrücken als Funktion der Zeit, also ) oder als Funktion des Ortes, also oder als Funktion des Ortes, also ) (oder als Funktion anderer Größen). (oder als Funktion anderer Größen).
Für den ersten Aufgabenteil ist das egal, weil die Beschleunigung konstant ist und zwar sowohl bezüglich des Ortes, als auch der Zeit. Beim zweiten Aufgabenteil hingegen ändert sich jedoch die Beschleunigung und zwar bezüglich des Ortes anders als bezüglich der Zeit. Hier ergeben sich also jeweils andere funktionale Zusammenhänge.
Viele Grüße,
Nils
|
|
 |
Nils Hoppenstedt

Anmeldungsdatum: 08.01.2020
Beiträge: 2022
|
 Nils Hoppenstedt Verfasst am: 28. Jul 2020 18:16 Titel: Nils Hoppenstedt Verfasst am: 28. Jul 2020 18:16 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | | PPS @Nils: Ich denke, die Geschwindigkeit nach Entspannung des Seils kann auch einfach in Abhängigkeit von l angegeben werden. |
Ja stimmt, l ist ja ebenfalls gegeben! 
Dann ist die Geschwindigkeit natürlich einfach  . .
Nils
|
|
 |
|



















