| Autor |
Nachricht |
Phase1997
Anmeldungsdatum: 22.07.2018
Beiträge: 14
|
 Phase1997 Verfasst am: 16. Jul 2020 14:43 Titel: Zweiteilchenzustand von ununterscheidbaren Fermionen Phase1997 Verfasst am: 16. Jul 2020 14:43 Titel: Zweiteilchenzustand von ununterscheidbaren Fermionen |
 |
|
Ich habe hier eine Aufgabe vor mir liegen, bei der ich vermute, dass sie falsch gestellt ist. Das ist aber natürlich immer bisschen gewagt, wenn man nicht den kompletten Durchblick hat. Ich hoffe, jemand kann etwas valides dazu sagen: 
Betrachtet man den Zweiteilchenzustand von ununterscheidbaren Fermionen:

 sind komplexe Koeffizienten und sind komplexe Koeffizienten und  die Erzeugungsoperatoren für ein Fermionen. die Erzeugungsoperatoren für ein Fermionen.
Aufgabe:
Warum kann man ohne Beschränkung der Allgemeinheit annehmen, dass die Matrix  antisymmetrisch ist? antisymmetrisch ist?
Meine Lösung wäre:
Da es ein Fermionzustand ist, muss gelten:

Berechnet man das unter der Verwendung des Antikommutators für die Erzeugungsoperatoren für Fermionen:

Das deutet ja darauf hin, dass  gelten muss, damit die obige Bedingung erfüllt ist. Aber das würde ja auch bedeuten, dass die Matrix nicht wie gefordert als Antisymmetrisch angenommen werden kann, sondern als symmterisch. gelten muss, damit die obige Bedingung erfüllt ist. Aber das würde ja auch bedeuten, dass die Matrix nicht wie gefordert als Antisymmetrisch angenommen werden kann, sondern als symmterisch.
Wo liegt mein Fehler?
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18108
|
 TomS Verfasst am: 16. Jul 2020 16:26 Titel: TomS Verfasst am: 16. Jul 2020 16:26 Titel: |
 |
|
Zunächst lassen wir Summenzeichen und Dagger weg um Schreibarbeit zu sparen; implizite Summation über doppelte Indizes ist ohnehin häufig üblich.
Zunächst sehen wir, dass der Diagonalterm mu = nu immer Null ist, da das Quadrat eines fermionischen Operators aufgrund des Antikommutators Null ergibt.
Dann schreiben wir die Matrix a als Summe einer symmetrischen S und einer antisymmetrischen Matrix A

und betrachten im Folgenden nur die nicht-diagonalen Terme.
Für den ersten Term mit S gilt
 = (+ S_{\nu\mu}) (- c_\nu c_\mu) = - S_{\mu\nu} c_\mu c_\nu = 0)
Die Gleichheitszeichen und Vorzeichen folgen von links nach rechts mittels Vertauschen der Operatoren, Transposition von S sowie Umbenennen der Indizes; das letzte Gleichheitszeichen folgt aus

Für den zweiten Term mit A gilt
 = (- A_{\nu\mu}) (- c_\nu c_\mu) = + A_{\mu\nu} c_\mu c_\nu)
Die Gleichheitszeichen und Vorzeichen folgen von links nach rechts mittels Vertauschen der Operatoren, Transposition von S sowie Umbenennen der Indizes.
Es trägt also nur der antisymmetrische Anteil A der Matrix a bei.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 16. Jul 2020 17:35, insgesamt einmal bearbeitet |
|
 |
Phase1997
Anmeldungsdatum: 22.07.2018
Beiträge: 14
|
 Phase1997 Verfasst am: 16. Jul 2020 17:18 Titel: Phase1997 Verfasst am: 16. Jul 2020 17:18 Titel: |
 |
|
vielen Dank für die Antwort!
Deine Lösung ist von der Argumentation soweit klar. Es gibt nur noch kleine Ungereimtheiten bei mir:
Wieso kann ich bei dem Schritt
\left(-c_{\nu} c_{\mu}\right)=-S_{\mu \nu} c_{\mu} c_{\nu}=0 )
einfach die Indizes ohne weiteres Umbenennen? Das wirkt etwas getrickst, da es für mich ja eingentlich einem Vertauschen der Operatoren gleich kommt.
In
\left(-c_{\nu} c_{\mu}\right)=+S_{\mu \nu} c_{\mu} c_{\nu} )
ist das S sicher ein Schreibfehler. Da sollte A stehen, richtig?
Noch eine letzte Frage:
Wo ist der Denkfehler in meiner Lösung? Gibt es eine Parallele zu deiner Argumentation?
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18108
|
 TomS Verfasst am: 16. Jul 2020 17:41 Titel: TomS Verfasst am: 16. Jul 2020 17:41 Titel: |
 |
|
Fangen wir von hinten an:
Den Denkfehler werde ich zu finden versuchen.
S statt A war ein Fehler, hab‘s korrigiert.
Zu den Indizes mit impliziter Summation: warum soll ich nicht folgende Umbenennung durchführen

... sind doch nur Indizes ...
Oder wenn du auf die Reihenfolge abzielst:

Es wird eh‘ über alles summiert.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Jul 2020 17:54 Titel: index_razor Verfasst am: 16. Jul 2020 17:54 Titel: |
 |
|
| Phase1997 hat Folgendes geschrieben: |
Noch eine letzte Frage:
Wo ist der Denkfehler in meiner Lösung? Gibt es eine Parallele zu deiner Argumentation? |
Ich denke der Fehler liegt hier in der zweiten Gleichung:
| Zitat: |

|
Der Operator  ist linear. Trotzdem hast du einfach die Indizes an der Matrix ist linear. Trotzdem hast du einfach die Indizes an der Matrix  mit vertauscht. Damit hast du den Zustand unverändert gelassen und lediglich die Indizes umbenannt. mit vertauscht. Damit hast du den Zustand unverändert gelassen und lediglich die Indizes umbenannt.
Korrekt wäre

Aus der letzten Gleichung folgt dann auch

|
|
 |
Phase1997
Anmeldungsdatum: 22.07.2018
Beiträge: 14
|
 Phase1997 Verfasst am: 16. Jul 2020 18:15 Titel: Phase1997 Verfasst am: 16. Jul 2020 18:15 Titel: |
 |
|
Das kann gut sein, dass da mein Fehler liegt. Da machst du deinem Namen alle Ehre 
| index_razor hat Folgendes geschrieben: |
Korrekt wäre

Aus der letzten Gleichung folgt dann auch
 |
Welche letzte Gleichung meinst du genau? Weil aus der oberen Gleichung des Zitates sehe ich noch nicht, wie die Antisymmetrie der Matrix zwangsläufig folgt. Aber das würde ja auch auf die Lösung von TomS als den richtigen Weg hindeuten.
|
|
 |
Phase1997
Anmeldungsdatum: 22.07.2018
Beiträge: 14
|
 Phase1997 Verfasst am: 16. Jul 2020 18:24 Titel: Phase1997 Verfasst am: 16. Jul 2020 18:24 Titel: |
 |
|
| TomS hat Folgendes geschrieben: | Fangen wir von hinten an:
Den Denkfehler werde ich zu finden versuchen.
S statt A war ein Fehler, hab‘s korrigiert.
Zu den Indizes mit impliziter Summation: warum soll ich nicht folgende Umbenennung durchführen

... sind doch nur Indizes ...
Oder wenn du auf die Reihenfolge abzielst:

Es wird eh‘ über alles summiert. |
Ok, jetzt ist mir dein Lösungsansatz klar geworden! Vielen Dank, das hat sehr geholfen! 
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Jul 2020 18:38 Titel: index_razor Verfasst am: 16. Jul 2020 18:38 Titel: |
 |
|
| Phase1997 hat Folgendes geschrieben: |
| index_razor hat Folgendes geschrieben: |
Korrekt wäre

Aus der letzten Gleichung folgt dann auch
 |
Welche letzte Gleichung meinst du genau?
|
Diese

Durch Umbenennen der Indizes  , wie von TomS erklärt, bringst du das auf die Form , wie von TomS erklärt, bringst du das auf die Form
 c_{\nu}^{+}c_{\mu}^{+}\left| 0 \right> = 0)
Aus der linearen Unabhängigkeit der  folgt dann die Asymmetrie von folgt dann die Asymmetrie von  . .
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 16. Jul 2020 18:58 Titel: index_razor Verfasst am: 16. Jul 2020 18:58 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
Aus der linearen Unabhängigkeit der  folgt dann die Asymmetrie von folgt dann die Asymmetrie von  . . |
Das gilt allerdings nur, wenn die Basiselemente  nicht schon aus dem antisymmetrischen Zweiteilchenraum stammen. Ansonsten gilt ja nicht schon aus dem antisymmetrischen Zweiteilchenraum stammen. Ansonsten gilt ja  und damit folgt nur, daß man und damit folgt nur, daß man  antisymmetrisch wählen kann, wie die Aufgabe behauptet. Genauer gesagt: antisymmetrisch wählen kann, wie die Aufgabe behauptet. Genauer gesagt:
 = \sum_{\mu<\nu} (a_{\mu\nu} - a_{\nu\mu})c_{\mu}^{+}c_{\nu}^{+}|0\rangle)
Das heißt nur der antisymmetrische Anteil von  trägt zur Summe bei, die Diagnoalelemente sind beliebig. trägt zur Summe bei, die Diagnoalelemente sind beliebig.
|
|
 |
Phase1997
Anmeldungsdatum: 22.07.2018
Beiträge: 14
|
 Phase1997 Verfasst am: 17. Jul 2020 20:20 Titel: Phase1997 Verfasst am: 17. Jul 2020 20:20 Titel: |
 |
|
Falls es nicht zuviel verlangt ist, würde ich mich sehr über ein kleines ok zu der nächsten Aufgabe freuen. Es ist etwas schwierig einzuschätzen, ob man richtig liegt, wenn man nicht komplett durch die Schreibweise blickt:
Die Aufgabe ist: Berechnen Sie das Skalarprodukt  . .
Unter welchen Bedingungen für  normiert? Was folgt, wenn die Matrix antisymmterisch ist. normiert? Was folgt, wenn die Matrix antisymmterisch ist.
Für das Skalarprodukt komme ich auf:

Wenn der Zustand normiert ist, muss für die Matrix  =1 gelten. Sind hier die Reihenfolge der Indizes korrekt? =1 gelten. Sind hier die Reihenfolge der Indizes korrekt?
Weil wenn diese nun antisymmetrisch ist, gilt

was ja irgendwie nicht sein kann.
Angenommen ich habe einen Zustand der Form

gilt dann also nicht
 ? Das hatte ich bei der Bestimmung der Normierung angesetzt. ? Das hatte ich bei der Bestimmung der Normierung angesetzt.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 17. Jul 2020 21:38 Titel: index_razor Verfasst am: 17. Jul 2020 21:38 Titel: |
 |
|
Die Basiszustände  sind antisymmetrisch und deswegen wie folgt normiert sind antisymmetrisch und deswegen wie folgt normiert

|
|
 |
Phase1997
Anmeldungsdatum: 22.07.2018
Beiträge: 14
|
 Phase1997 Verfasst am: 17. Jul 2020 23:26 Titel: Phase1997 Verfasst am: 17. Jul 2020 23:26 Titel: |
 |
|
|
Das hilft mir leider nicht weiter. Ist damit meine Bedingung für a falsch, die aus der nirmierung des Zustandes folgt? Also doch die indizes tauschen? Weil dass die Operatoren beim skalarprodukt verschwinden bin ich mir eigentlich durch anwenden des antikommutstors ziemlich sicher.
|
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 18. Jul 2020 07:37 Titel: index_razor Verfasst am: 18. Jul 2020 07:37 Titel: |
 |
|
| Phase1997 hat Folgendes geschrieben: | Das hilft mir leider nicht weiter. Ist damit meine Bedingung für a falsch, die aus der nirmierung des Zustandes folgt?
|
Natürlich ist die Bedingung falsch. Wie du ja selbst feststellst, kann eine Summe von negativen Zahlen nicht 1 ergeben. Wie genau bist du denn darauf gekommen? Meine Annahme war, daß du eine falsche Normierung der Basisvektoren verwendet hast.
| Zitat: |
Also doch die indizes tauschen? Weil dass die Operatoren beim skalarprodukt verschwinden bin ich mir eigentlich durch anwenden des antikommutstors ziemlich sicher. |
Was soll das bedeuten? Welche Operatoren verschwinden? Welche Indizes willst du vertauschen?
Du startest mit

Also folgt

Wie rechnest du jetzt weiter?
|
|
 |
Phase1997
Anmeldungsdatum: 22.07.2018
Beiträge: 14
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18108
|
 TomS Verfasst am: 18. Jul 2020 09:34 Titel: TomS Verfasst am: 18. Jul 2020 09:34 Titel: |
 |
|
Das kannst du dir doch selbst überlegen:

Das setzt du jetzt in

ein und verwendest

Bei mehreren Operatoren funktioniert das analog: alle Vernichter nach rechts durchtauschen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 18. Jul 2020 10:06 Titel: index_razor Verfasst am: 18. Jul 2020 10:06 Titel: |
 |
|
| Phase1997 hat Folgendes geschrieben: | Im folgenden Bild ist nochmal meine erste Lösung zu sehen und die neue:
[img] https://ibb.co/g6cQjks [/img] (dasselbe Bild ist nochmal angehängt, falls jemand den Link nicht anklicken möchte)
|
In der zweiten Rechnung hast du irgendwann mal die Doppelsumme über  unterschlagen. War das Absicht? Damit sieht es nämlich so aus, als würde die Normierungsbedingung für jeden Koeffizienten unterschlagen. War das Absicht? Damit sieht es nämlich so aus, als würde die Normierungsbedingung für jeden Koeffizienten  einzeln gelten. einzeln gelten.
| Zitat: |
Ich frage mich jetzt nur: Gilt dann für beispielsweise

auch sowas

?
|
Was soll hier gelten? Das ist nur ein einzelner Term, keine Gleichung. Fragst du, ob dieses Skalarprodukt für  ungleich null ist? Dann lautet die Antwort ja, denn es ist ja gleich der Norm des Vektors ungleich null ist? Dann lautet die Antwort ja, denn es ist ja gleich der Norm des Vektors  , also 1. , also 1.
| Zitat: |
Das wird zwar eh null, wenn 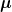 und und 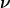 ungleich sind, aber rein formal: Muss ich für das Skalarprodukt immer beachten, dass die Indizes wechseln, wenn ich die Bra-Vektor betrachte? Oder kommt das nur durch das Summenzeichen in der eigentlichen Aufgabe? ungleich sind, aber rein formal: Muss ich für das Skalarprodukt immer beachten, dass die Indizes wechseln, wenn ich die Bra-Vektor betrachte? Oder kommt das nur durch das Summenzeichen in der eigentlichen Aufgabe? |
Was meinst du damit, daß die Indizes wechseln? Meinst du, daß sie irgendwo Vertauschen oder daß man zwei unabhängige Sätze von Indizes  und und  verwenden muß? verwenden muß?
|
|
 |
Phase1997
Anmeldungsdatum: 22.07.2018
Beiträge: 14
|
 Phase1997 Verfasst am: 18. Jul 2020 10:21 Titel: Phase1997 Verfasst am: 18. Jul 2020 10:21 Titel: |
 |
|
Tut mir leid, wenn ich triviale Fragen stelle, aber ich sitze hier ja schon seit Tagen vor dem ganzen Indizes und hab mich da eigentlich fit und relativ sicher gefühlt. Nur sehe ich bei meinen Lösungen, dass dann immer wieder das Verständnis oder das Wissen bei grundlegendsten Sachen fehlt. Die Berechnungen kriege ich soweit alle hin, aber wenn ich im ersten Schritt was falsches ansetze, bringt mir das ja nichts.
Mir ist klar, dass

gilt. Also ist das Skalarprodukt so definiert, dass immer unterschiedliche Indizes für die Operatoren verwendet wird und dann durch Relationen auf das Ergebnis geschlossen wird? Für mich ist das eine Frage von Defintion.
Ich frage das nochmal so genau, weil ich für die obere Aufgabe

angesetzt hatte, was ja falsch ist. Warum das falsch ist, ist mir mitterweile auch soweit klar und dass in dem Fall

richtig ist. Danke auch nochmal dafür! Ich versuche mir das nur soweit klar zu machen, dass ich da was allgemein gültiges draus ziehe.
Mir tut es wirklich leid, wenn meine Fragen sehr grundlegend sind. Aber Uni ist zu, Kommilitonen sind sich auch unsicher und Lehrbücher bringen mir für die spezfischen Fälle keine Sicherheit.
|
|
 |
Phase1997
Anmeldungsdatum: 22.07.2018
Beiträge: 14
|
 Phase1997 Verfasst am: 18. Jul 2020 10:29 Titel: Phase1997 Verfasst am: 18. Jul 2020 10:29 Titel: |
 |
|
| index_razor hat Folgendes geschrieben: |
In der zweiten Rechnung hast du irgendwann mal die Doppelsumme über  unterschlagen. War das Absicht? Damit sieht es nämlich so aus, als würde die Normierungsbedingung für jeden Koeffizienten unterschlagen. War das Absicht? Damit sieht es nämlich so aus, als würde die Normierungsbedingung für jeden Koeffizienten  einzeln gelten. einzeln gelten.
|
Ja das war mehr oder weniger Absicht. Also mir ist bewusst, dass da noch die Summe hinkommt.
| Zitat: |
Was meinst du damit, daß die Indizes wechseln? Meinst du, daß sie irgendwo Vertauschen oder daß man zwei unabhängige Sätze von Indizes  und und  verwenden muß? verwenden muß? |
Ja, warum muss man zwei unabhängige Sätze verwenden? Also wie schon geschrieben, macht das in dem Fall Sinn. Nur ist das eine allgemeine Aussage, dass man zwei Sätze verwenden muss oder kommt das ausschließlich vom Summenzeichen, dass man eben über alles drüber summiert? Meine Vermutung ist letzteres?
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18108
|
 TomS Verfasst am: 18. Jul 2020 10:48 Titel: TomS Verfasst am: 18. Jul 2020 10:48 Titel: |
 |
|
Man muss natürlich zwei unabhängige Sätze verwenden.
Bsp. für Vektoren x mit reellen Koordinaten x_mu und Einheitsvektoren e_mu:

 \cdot \left(\sum_\nu x_\nu e_\nu \right))
Im nächsten Schritt dann Orthonormiertheit der Einheitsvektoren

und erst damit

Schau dir mal an, was passiert, wenn du beide Summen über mu bilden möchtest: s.u. index_razor.
| Phase1997 hat Folgendes geschrieben: | | Also ist das Skalarprodukt so definiert, dass immer unterschiedliche Indizes für die Operatoren verwendet wird und dann durch Relationen auf das Ergebnis geschlossen wird? Für mich ist das eine Frage von Definition. |
Die Definition erfolgt in dem Moment, wo du Vektoren bzw. Zustände und Operatoren bzgl. einer Basis definierst, also letztlich die Eigenschaften eines linearen Vektorraumes nutzt. Der resultierende Vektor ist unabhängig von den eingeführten Indizes, weil über diese summiert wird.
| Phase1997 hat Folgendes geschrieben: | | Nur ist das eine allgemeine Aussage, dass man zwei Sätze verwenden muss oder kommt das ausschließlich vom Summenzeichen, dass man eben über alles drüber summiert? Meine Vermutung ist letzteres? |
Die Ursache ist häufig die Darstellung der Objekte im Kontext eines linearen Vektorraumes. Daraus resultiert dann die Summe, im Falle eines „kontinuierlichen Index“ wie x,p ein Integral.
Faustregel: wenn ein Term über einen Index summiert wird, dann tritt dieser Index genau zweimal da; alles andere ist zu 99 % falsch.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 18. Jul 2020 12:50, insgesamt 2-mal bearbeitet |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 18. Jul 2020 12:28 Titel: index_razor Verfasst am: 18. Jul 2020 12:28 Titel: |
 |
|
| Phase1997 hat Folgendes geschrieben: |
Mir ist klar, dass

gilt. Also ist das Skalarprodukt so definiert, dass immer unterschiedliche Indizes für die Operatoren verwendet wird und dann durch Relationen auf das Ergebnis geschlossen wird? Für mich ist das eine Frage von Defintion.
|
| Phase1997 hat Folgendes geschrieben: |
Ja, warum muss man zwei unabhängige Sätze verwenden? Also wie schon geschrieben, macht das in dem Fall Sinn. Nur ist das eine allgemeine Aussage, dass man zwei Sätze verwenden muss oder kommt das ausschließlich vom Summenzeichen, dass man eben über alles drüber summiert? Meine Vermutung ist letzteres?
|
Das ist keine Frage der Definition. Wenn du ein Produkt von zwei Summen bildest, mußt du alle Summanden der ersten Summe mit allen Summanden der zweiten Summe multiplizieren und am Ende alle Produkte addieren. Wenn beide Summen von 1 bis n gehen, sind das  Summanden im Ergebnis. Das hat nichts mit Quantenmechanik, Operatoren oder Hilbertraum zu tun. Dieselben Regeln gelten auch für gewöhnliche Zahlen. (Dort nennt man sie Distributivregel, im Hilbertraum Sesquilinearität des Skalarprodukts.) Summanden im Ergebnis. Das hat nichts mit Quantenmechanik, Operatoren oder Hilbertraum zu tun. Dieselben Regeln gelten auch für gewöhnliche Zahlen. (Dort nennt man sie Distributivregel, im Hilbertraum Sesquilinearität des Skalarprodukts.)
Beispiel: \cdot(b_1 + b_2 + \cdots + b_n) = a_1 b_1 + a_1 b_2 +\cdots + a_1 b_n + a_2 b_1 + a_2 b_2 + \cdots + a_2 b_n + \cdots + a_n b_{n-1} + a_{n} b_n)
Wie würdest du nun die rechte Seite mit Summensymbol schreiben?

ergibt offensichtlich etwas anderes, denn es fehlen die Terme, in denen a und b verschiedenen Indizes haben.
Korrekt wäre also

|
|
 |
|

















