| Autor |
Nachricht |
Tim2002
Anmeldungsdatum: 06.03.2020
Beiträge: 1
|
 Tim2002 Verfasst am: 06. März 2020 15:11 Titel: Wieso ist Lichtgeschwindigkeit absolut? |
 |
|
Meine Frage:
Hallo ich bin neu hier und kenn mich ehrlich gesagt nicht so gut mit Physik aus.Kürzlich habe ich mir ein Buch über die Relativitätstheorie gekauft einfach weil ich mal wissen wollte was sie aussagt.
An einem Punkt hänge ich mich jedoch die ganze Zeit auf.
Die RT besagt ja, dass c konstant ist, also egal in welchem Bezugssystem im Vakuum immer ca. 300.000 m/s schnell ist.
Ich frage mich wie das möglich ist.
Ist das eine Eigenschaft des Licht selbst oder des Raums?
In meinem Denkansatz wird Licht von einer Lichtquelle abgegeben und breitet sich von dort eben mit dieser konstanten Geschwindigkeit aus!?
Wieso ist aber nicht möglich dass das Licht sich gemäß des Relativitätsprinzips relativ zu einem sich bewegenden Körper langsamer bewegt?
Tut mir leid für meine Unwissenheit aber auf anderen Seiten habe ich keine Antworten gefunden und im Buch wird nur Entdeckung dieses Verhaltens durch die Maxwellgleichungen beschrieben.
Danke schonmal im voraus.
Meine Ideen:
-
|
|
 |
as_string
Moderator
Anmeldungsdatum: 09.12.2005
Beiträge: 5785
Wohnort: Heidelberg
|
| as_string Verfasst am: 06. März 2020 16:24 Titel: |
|
|
Ich würde sagen, das ist eine Eigenschaft der Raumzeit.
Letztlich kann man das nicht wirklich begründen, sondern umgekehrt: Wir messen, dass das so ist: Egal, wie sich die Lichtquelle bewegt und egal, wie sich der Beobachter bewegt: Er misst immer dieselbe (Vakuums-)Lichtgeschwindigkeit.
Diese Feststellung hat natürlich gerade zu solchen "Problemen" geführt, wie Du sich beschreibst: Wenn ich eine Gewehrkugel beobachte, dann hat die doch eine unterschiedliche Geschwindigkeit, je nachdem, wie sich Schütze beim Abschießen und Beobachter gerade bewegen. Warum sollte das bei Licht anders sein und wie ist das überhaupt möglich.
Die Lösung für diese Frage ist dann eben die Relativitätstheorie, die man direkt aus dieser beobachteten Konstanz der Lichtgeschwindigkeit herleiten kann.
Gruß
Marco
|
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18030
|
| TomS Verfasst am: 07. März 2020 07:26 Titel: |
|
|
Es liegt an der minkowskischen (riemannschen) Geometrie der Raumzeit und ihrer Symmetrie unter (lokalen) Lorentztransformationen in der speziellen (allgemeinen) Relativitätstheorie.
Betrachte ein Objekt der Masse Null. Für einen bestimmten Beobachter B in dessen Ruhesystem mit Koordinaten x, t gilt für die Bewegung eines lichtartigen Teilchens
 - ct = 0)
Für einen anderen Beobachter B‘ mit anderen Koordinaten x‘, t‘ gilt
 - ct^\prime = 0)
Diese Invarianz (die Invariante ist hier die Null) kann als verallgemeinerter Abstand in der 4-dim. Raumzeit betrachtet werden. Entlang lichtartiger Weltlinien gilt für den infinitesimalen Abstand ds eines infinitesimalen Abschnitts der Weltlinie
Das ist eine rein geometrische Definition; sie gilt unabhängig davon, ob ein reales lichtartiges Teilchen vorliegt.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Brillant
Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
| Brillant Verfasst am: 07. März 2020 15:57 Titel: |
|
|
Ist es richtig, dass jeder Beobachter, egal wie schnell er sich bewegt, immer die Lichtgeschwindigkeit c mißt?
Er beschleunigt und sein Licht-Tacho steht weiterhin auf Null.
Woher weiß dann der Beobachter, dass er nicht mehr schneller werden darf, wenn sein Tacho immer auf Null steht?
Setzt dann die „spukhafte Fernwirkung” einer Regie ein, wie immer man die nennen mag?
|
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3392
|
| ML Verfasst am: 07. März 2020 17:55 Titel: |
|
|
Hallo,
| Brillant hat Folgendes geschrieben: | Ist es richtig, dass jeder Beobachter, egal wie schnell er sich bewegt, immer die Lichtgeschwindigkeit c mißt?
|
er misst für das Licht immer die Lichtgeschwindigkeit, egal, ob er vor dem Licht davonläuft oder ihm entgegeneilt.
Viele Grüße
Michael
|
|
|
Brillant
Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
| Brillant Verfasst am: 07. März 2020 20:31 Titel: |
|
|
Hallo Michael,
| ML hat Folgendes geschrieben: | | er misst für das Licht immer die Lichtgeschwindigkeit, egal, ob er vor dem Licht davonläuft oder ihm entgegeneilt. |
Gut, meine rhetorische Frage hast du beantwortet.
Und weiter? Wenn sich jemand in Bezug auf Licht nicht bewegen kann, wieso soll dann die Lichtgeschwindigkeit eine Grenze sein?
|
|
|
hansguckindieluft
Anmeldungsdatum: 23.12.2014
Beiträge: 1212
|
| hansguckindieluft Verfasst am: 07. März 2020 20:59 Titel: |
|
|
| Brillant hat Folgendes geschrieben: |
...wieso soll dann die Lichtgeschwindigkeit eine Grenze sein? |
Weil die relativistische Masse bei Lichtgeschwindigkeit unendlich wird, und daher für jede weitere Beschleunigung eine unendlich große Kraft benötigt würde.
|
|
|
Brillant
Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
| Brillant Verfasst am: 07. März 2020 21:05 Titel: |
|
|
Genau das verstehe ich nicht. Der Beobachter hat doch gar keine Geschwindigkeit.
Was zum Teifel ist mit dieser Grenzgeschwindigkeit gemeint, bezogen auf seinen Startplatz? Bezogen auf ein unsichtbares Gitter im Raum?
|
|
|
hansguckindieluft
Anmeldungsdatum: 23.12.2014
Beiträge: 1212
|
| hansguckindieluft Verfasst am: 07. März 2020 21:24 Titel: |
|
|
| Brillant hat Folgendes geschrieben: | | Genau das verstehe ich nicht. Der Beobachter hat doch gar keine Geschwindigkeit. |
Welcher Beobachter?
| Brillant hat Folgendes geschrieben: |
Was zum Teifel ist mit dieser Grenzgeschwindigkeit gemeint, bezogen auf seinen Startplatz? Bezogen auf ein unsichtbares Gitter im Raum? |
Die Grenzgeschwindigkeit ist die Lichtgeschwindigkeit. Und die ist unabhängig vom Bezugssystem. Überlichtgeschwindigkeit ist in jedem Bezugssystem Überlichtgeschwindigkeit. Und Unterlichtgeschwindigkeit ist in jedem Bezugssystem Unterlichtgeschwindigkeit.
|
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3392
|
| ML Verfasst am: 07. März 2020 23:37 Titel: |
|
|
Hallo,
| Brillant hat Folgendes geschrieben: | | Gut, meine rhetorische Frage hast du beantwortet. |
schön. Dann ist ja alles geklärt.
| Zitat: |
Und weiter? Wenn sich jemand in Bezug auf Licht nicht bewegen kann, wieso soll dann die Lichtgeschwindigkeit eine Grenze sein? |
Ist es Dir langweilig?
Viele Grüße
Michael
|
|
|
Brillant
Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
| Brillant Verfasst am: 25. März 2020 01:12 Titel: |
|
|
Habe ich das so seltsam formuliert oder wollt ihr mich nicht verstehen?
Noch mal von vorn: Eine Rakete hat eine undefinierte Geschwindigkeit. Das Licht saust an ihr vorbei mit Lichtgeschwindigkeit.
Nun gibt der Pilot Gas (oder Elektronen oder was auch immer), er spürt die Beschleunigung, denn er wird in seinen Sitz gedrückt.
Nach einer Weile möchte er seine neue Geschwindigkeit bestimmen, wie geht das? In Bezug auf das Licht ist er ja offenbar nicht schneller geworden. Und eine Staudrucksonde (dient unter anderem bei Flugzeugen, Hubschraubern und Rennfahrzeugen zur Geschwindigkeitsmessung) funktioniert im Vakuum ja nicht.
Also beschleunigt er weiter. Und weiter und weiter ...
Wann hat er denn nun die Maximalgeschwindigkeit erreicht? Und wie bestimmt er sie?
|
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3392
|
| ML Verfasst am: 25. März 2020 01:22 Titel: |
|
|
Hallo,
| Brillant hat Folgendes geschrieben: | | Wann hat er denn nun die Maximalgeschwindigkeit erreicht? Und wie bestimmt er sie? |
Um eine Geschwindigkeit zu bestimmen, muss man zunächst ein Bezugssystem definieren.
| Brillant hat Folgendes geschrieben: | | Was zum Teifel ist mit dieser Grenzgeschwindigkeit gemeint, bezogen auf seinen Startplatz? Bezogen auf ein unsichtbares Gitter im Raum? |
Gemeint ist die Geschwindigkeit, die ein anderes Objekt in Bezug auf Dich hat, wobei Du Dich als ruhend annimmst.
Viele Grüße
Michael
|
|
|
Brillant
Anmeldungsdatum: 12.02.2013
Beiträge: 1973
Wohnort: Hessen
|
| Brillant Verfasst am: 25. März 2020 01:52 Titel: |
|
|
Okay, du arbeitest an deiner Antwort ...
„Gemeint ist die Geschwindigkeit, die ein anderes Objekt in Bezug auf Dich hat, wobei Du Dich als ruhend annimmst. ”
Gut, der Antrieb setzt aus, die Rakete beschleunigt nicht mehr, ich bin Passagier und darf mich als ruhend annehmen.
Zur Geschwindigkeitsbestimmung im interstellaren Raum suche ich mir nun eine Galaxie aus, die von meinem Heimatplaneten eine bestimmte Rotverschiebung hatte. Ist die Rotverschiebung durch die Beschleunigung auf sie zu geringer geworden?
Nun beschleunigt die Rakete wieder, die Rotverschiebung wird kleiner und geht über in Blauverschiebung, nun holen wir die Galaxie in ihrer Fluchtbewegung ein.
Mir ist immer noch nicht klar, wann die Beschleunigung keinen weiteren Geschwindigkeitszuwachs mehr bewirkt. Und wenn, dann muss ich mir eine andere flüchtende Galaxis suchen und es geht weiter?
|
|
|
ML
Anmeldungsdatum: 17.04.2013
Beiträge: 3392
|
| ML Verfasst am: 25. März 2020 02:47 Titel: |
|
|
Hallo,
| Brillant hat Folgendes geschrieben: | | Gut, der Antrieb setzt aus, die Rakete beschleunigt nicht mehr, ich bin Passagier und darf mich als ruhend annehmen. |
Wieso muss es gleich eine Galaxie sein? Ich schlage vor, wir betrachten ein Teilchen in einem Teilchenbeschleuniger. Dann müssen wir nicht die Expansion des Universums o. ä. betrachten und müssen uns nicht nur vorstellen, was vielleicht passieren könnte, sondern wir können über Experimente besprechen, die schon tatsächlich durchgeführt wurden.
Bezugssystem ist das Laborsystem. In einem Teilchenbeschleuniger beschleunigst du mithilfe einer (evtl. mehrfach angewandten) Beschleunigungsspannung ein Elektron. Das funktioniert so ähnlich wie in einem Röhrenfernseher, allerdings mit höheren Spannungen.
Die kinetische Energie, die das Teilchen hat, lässt sich über die Spannung leicht ausrechnen. Es gilt
mit der Ladung  eines Elektrons und der Beschleunigungsspanung  .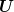
Nach klassischer Rechnung gilt:
mit der Masse 
Wenn Du die Gleichung nach U umstellst, erhältst Du:
Nun kannst Du als Geschwindigkeit beispielsweise  einsetzen. Du erhältst dann die Energie, die man nach klassischer Rechnung bräuchte, um das Elektron auf die Lichgeschwindigkeit zu beschleunigen. Bloß: Die tatsächliche Geschwindigkeit erweist sich im Experiment als geringer.
Eine Übereinstimmung mit den tatsächlichen Messungen tritt ein, wenn Du die relativistische Gleichung für die kinetische Energie nutzt:
 m c^2) mit dem Lorentzfaktor ^2}})
Du setzt dann als Gleichung an:
^2}} - 1\right) m_\mathrm{e} \cdot c^2)
und formst nach v um.
Hier:
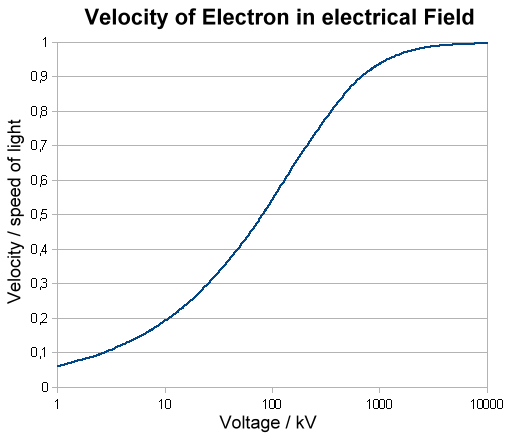
https://de.wikipedia.org/wiki/Kinetische_Energie#/media/Datei:Elektronengeschwindigkeit.png
kannst Du sehen, wie sich die Geschwindigkeit mit steigender Energie immer näher an die Lichtgeschwindigkeit annähert.
| Zitat: | | Mir ist immer noch nicht klar, wann die Beschleunigung keinen weiteren Geschwindigkeitszuwachs mehr bewirkt. |
Wechseln wir einmal das Bild wieder zu einem Raumschiff:
Es gibt keinen festen Punkt, ab dem das Gasgeben plötzlich nichts mehr nutzt. Das Gasgeben wirkt sich bloß aus Sicht des "zurückgebliebenen" Beobachters immer schwächer auf die Geschwindigkeit aus, je größer die Geschwindigkeit schon ist.
Das hat aber nichts mit einer immer schwächer werdenden Funktion des Gaspedals zu tun oder damit, dass der Fahrer beim Gasgeben auf einmal weniger in den Fahrersitz gedrückt würde. Bei konstant durchgedrücktem Gaspedal fühlt sich für den Raumfahrer die Situation immer gleich an.
Das eigentliche Problem ist, dass die Begriffe und Größen der klassischen Mechanik nicht besonders gut geeignet sind, um solche relativistischen Effekte zu beschreiben.
Viele Grüße
Michael
| Beschreibung: |
|
| Dateigröße: |
15.44 KB |
| Angeschaut: |
2418 mal |
|
Zuletzt bearbeitet von ML am 28. März 2020 01:56, insgesamt 6-mal bearbeitet |
|
|
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
| Ich Verfasst am: 25. März 2020 09:39 Titel: |
|
|
| Brillant hat Folgendes geschrieben: | Zur Geschwindigkeitsbestimmung im interstellaren Raum suche ich mir nun eine Galaxie aus, die von meinem Heimatplaneten eine bestimmte Rotverschiebung hatte. Ist die Rotverschiebung durch die Beschleunigung auf sie zu geringer geworden?
Nun beschleunigt die Rakete wieder, die Rotverschiebung wird kleiner und geht über in Blauverschiebung, nun holen wir die Galaxie in ihrer Fluchtbewegung ein.
Mir ist immer noch nicht klar, wann die Beschleunigung keinen weiteren Geschwindigkeitszuwachs mehr bewirkt. Und wenn, dann muss ich mir eine andere flüchtende Galaxis suchen und es geht weiter? |
Beschleunigung bewirkt immer eine Geschwindigkeitsänderung. Und die Blauverschiebung steigt exponentiell mit der Zeit, die du beschleunigst. Das hört nie auf.
Daran ändert auch nichts die Tatsache, dass die Geschwindigkeitsänderung relativ zu diesen oder jenen Objekten immer kleiner wird. Wenn du dir das nicht vorstellen kannst, dann nimm die Rapidität als Geschwindigkeitsmass, das ist vielleicht hilfreich.
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 26. März 2020 13:21 Titel: |
|
|
| Brillant hat Folgendes geschrieben: | | Mir ist immer noch nicht klar, wann die Beschleunigung keinen weiteren Geschwindigkeitszuwachs mehr bewirkt. |
Das passiert, wenn entgegen oder senkrecht zur Geschwindigkeit beschleunigt wird. Erfolgt die Beschleunigung in Richtung der Geschwindigkeit, dann bewirkt sie immer einen Geschwindigkeitszuwachs.
|
|
|
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 829
|
| Qubit Verfasst am: 26. März 2020 13:36 Titel: |
|
|
| Brillant hat Folgendes geschrieben: |
Mir ist immer noch nicht klar, wann die Beschleunigung keinen weiteren Geschwindigkeitszuwachs mehr bewirkt. Und wenn, dann muss ich mir eine andere flüchtende Galaxis suchen und es geht weiter? |
Die Geschwindigkeit ändert sich schon.
Aber die Beschleunigung nimmt bei konstanter Kraft ab, da die Trägheit der Masse mit der Geschwindigkeit zunimmt.
|
|
|
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
| Ich Verfasst am: 26. März 2020 14:52 Titel: |
|
|
| Qubit hat Folgendes geschrieben: | Die Geschwindigkeit ändert sich schon.
Aber die Beschleunigung nimmt bei konstanter Kraft ab, da die Trägheit der Masse mit der Geschwindigkeit zunimmt. |
Man sollte einfach mal die richtigen Begriffe aus dem Viererformalismus verwenden: Beschleunigung = Eigenbeschleunigung, Trägheit = Masse = Ruhemasse. F=m*a, fertig.
Dass sich die Geschwindigkeit in irgendwelchen Bezugssystemen nicht nach diesem Gesetz ändert ist eine rein kinematische Sache, keine Frage der Dynamik. Man sollte das Problem nicht auf die Dynamik schieben und mit richtungs- und geschwindigkeitsabhängiger Trägheit arbeiten, das geht komplett am Wesen der Dinge vorbei.
|
|
|
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 829
|
| Qubit Verfasst am: 26. März 2020 15:22 Titel: |
|
|
| Ich hat Folgendes geschrieben: | | Qubit hat Folgendes geschrieben: | Die Geschwindigkeit ändert sich schon.
Aber die Beschleunigung nimmt bei konstanter Kraft ab, da die Trägheit der Masse mit der Geschwindigkeit zunimmt. |
Man sollte einfach mal die richtigen Begriffe aus dem Viererformalismus verwenden: Beschleunigung = Eigenbeschleunigung, Trägheit = Masse = Ruhemasse. F=m*a, fertig.
Dass sich die Geschwindigkeit in irgendwelchen Bezugssystemen nicht nach diesem Gesetz ändert ist eine rein kinematische Sache, keine Frage der Dynamik. |
F=m*a gilt in der SRT nur im Grenzfall. Für "irgendwelche" (beschleunigte) BS macht die SRT gar keine Aussagen, sie setzt Inertialsysteme voraus.
Trägheit hängt von der Energie, nicht nur Ruhemasse, ab.
|
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 26. März 2020 15:59 Titel: |
|
|
| Qubit hat Folgendes geschrieben: | | Ich hat Folgendes geschrieben: |
Man sollte einfach mal die richtigen Begriffe aus dem Viererformalismus verwenden: Beschleunigung = Eigenbeschleunigung, Trägheit = Masse = Ruhemasse. F=m*a, fertig.
Dass sich die Geschwindigkeit in irgendwelchen Bezugssystemen nicht nach diesem Gesetz ändert ist eine rein kinematische Sache, keine Frage der Dynamik. |
F=m*a gilt in der SRT nur im Grenzfall.
|
Wenn a die Eigenbeschleunigung und m die Ruhemasse ist (wie Ich es gerade definiert hat), dann gilt es in der SRT universell für Punktmassen.
| Zitat: |
Für "irgendwelche" (beschleunigte) BS macht die SRT gar keine Aussagen, sie setzt Inertialsysteme voraus.
|
Das stimmt nicht. Meine Standardempfehlung zu dem Thema ist MTW, Gravitation, Kapitel 6.
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 26. März 2020 16:04 Titel: |
|
|
| Ich hat Folgendes geschrieben: | | Man sollte einfach mal die richtigen Begriffe aus dem Viererformalismus verwenden: |
Nur, wenn das auch alle Beteiligten verstehen.
| Ich hat Folgendes geschrieben: | | Beschleunigung = Eigenbeschleunigung |
Das gilt nur im tangential mitbewegten Inertialsystem.
| Ich hat Folgendes geschrieben: | | Trägheit = Masse = Ruhemasse. |
Die Masse ist zwar ein Maß für die Trägheit aber das heißt nicht, dass man beides gleichsetzen kann.
| Ich hat Folgendes geschrieben: | | F=m*a |
Das gilt zwar für Viererkraft und Viererbeschleunigung aber nicht für Kraft und Beschleunigung.
|
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 26. März 2020 16:23 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | Ich hat Folgendes geschrieben: | | Man sollte einfach mal die richtigen Begriffe aus dem Viererformalismus verwenden: |
Nur, wenn das auch alle Beteiligten verstehen.
|
Für die Beteiligten, auf die es ankommt, ist der Nutzen dieses Forums, daß sie hinterher mehr verstehen als vorher oder zumindest wissen, worüber sie sich informieren müssen.
| Zitat: |
| Ich hat Folgendes geschrieben: | | F=m*a |
Das gilt zwar für Viererkraft und Viererbeschleunigung aber nicht für Kraft und Beschleunigung. |
Es gilt auch für Eigenbeschleunigung und Kraft. Mehr wurde nicht behauptet.
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 26. März 2020 16:40 Titel: |
|
|
| index_razor hat Folgendes geschrieben: | | Es gilt auch für Eigenbeschleunigung und Kraft. Mehr wurde nicht behauptet. |
Die Behauptung war "F=m*a". Das ist mehr. Genauso wie die Behauptung "Beschleunigung = Eigenbeschleunigung" ist das nicht allgemein gültig.
|
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 26. März 2020 16:51 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Es gilt auch für Eigenbeschleunigung und Kraft. Mehr wurde nicht behauptet. |
Die Behauptung war "F=m*a". Das ist mehr.
|
Die Behauptung war "F=m*a" mit vorher definiertem a=Eigenbeschleunigung und m=Ruhemasse. Das ignorierst du offenbar aus diesem Grund:
| Zitat: |
Genauso wie die Behauptung "Beschleunigung = Eigenbeschleunigung" ist das nicht allgemein gültig. |
Das ist eine sinnvolle Definition von Beschleunigung. Woran du dich störst, ist nur, daß du Beschleunigung gern anders definierst. Solange man aber die Definitionen auseinanderhält, ist es nur eine Frage der Zweckmäßigkeit welche man verwendet.
|
|
|
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 829
|
| Qubit Verfasst am: 26. März 2020 18:04 Titel: |
|
|
| index_razor hat Folgendes geschrieben: | | Qubit hat Folgendes geschrieben: | | Ich hat Folgendes geschrieben: |
Man sollte einfach mal die richtigen Begriffe aus dem Viererformalismus verwenden: Beschleunigung = Eigenbeschleunigung, Trägheit = Masse = Ruhemasse. F=m*a, fertig.
Dass sich die Geschwindigkeit in irgendwelchen Bezugssystemen nicht nach diesem Gesetz ändert ist eine rein kinematische Sache, keine Frage der Dynamik. |
F=m*a gilt in der SRT nur im Grenzfall.
|
Wenn a die Eigenbeschleunigung und m die Ruhemasse ist (wie Ich es gerade definiert hat), dann gilt es in der SRT universell für Punktmassen.
| Zitat: |
Für "irgendwelche" (beschleunigte) BS macht die SRT gar keine Aussagen, sie setzt Inertialsysteme voraus.
|
Das stimmt nicht. Meine Standardempfehlung zu dem Thema ist MTW, Gravitation, Kapitel 6. |
Ja, man kann lokal in der SRT ein (geschwindigkeitsunabhängiges) Trägheitskraftfeld einführen. Dies ist ganz nützlich im Übergang zur ART.
Allerdings ist dieses Kraftfeld kein Grenzfall einer kovarianten Formulierung einer Minkowskikraft. So lassen sich Trägheitskräfte in der SRT zwar berücksichtigen, aber nicht in die Theorie integrieren.
|
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 26. März 2020 19:14 Titel: |
|
|
| Qubit hat Folgendes geschrieben: | | Zitat: |
Das stimmt nicht. Meine Standardempfehlung zu dem Thema ist MTW, Gravitation, Kapitel 6. |
Ja, man kann lokal in der SRT ein (geschwindigkeitsunabhängiges) Trägheitskraftfeld einführen. Dies ist ganz nützlich im Übergang zur ART.
Allerdings ist dieses Kraftfeld kein Grenzfall einer kovarianten Formulierung einer Minkowskikraft.
|
Die SRT kann trotzdem, entgegen deiner Behauptung, Aussagen über beschleunigte Bezugssysteme machen. Mit einem "Trägheitskraftfeld" oder einem "Grenzfall einer kovarianten Formulierung" hat das freilich nichts zu tun. Es klingt auch ehrlich gesagt ziemlich nach Kauderwelsch.
| Zitat: |
So lassen sich Trägheitskräfte in der SRT zwar berücksichtigen, aber nicht in die Theorie integrieren. |
Trägheitskräfte lassen sich problemlos in die SRT integrieren.
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 26. März 2020 23:26 Titel: |
|
|
| index_razor hat Folgendes geschrieben: | | Zitat: | | Genauso wie die Behauptung "Beschleunigung = Eigenbeschleunigung" ist das nicht allgemein gültig. |
Das ist eine sinnvolle Definition von Beschleunigung. |
Das ist keine Definition, sondern eine Gleichung. Eine Definition wäre "Beschleunigung := Eigenbeschleunigung", aber davon ist dringend abzuraten, weil der Begriff "Beschleunigung" bereits mit anderer Bedeutung etabliert ist.
|
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 27. März 2020 08:32 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Zitat: | | Genauso wie die Behauptung "Beschleunigung = Eigenbeschleunigung" ist das nicht allgemein gültig. |
Das ist eine sinnvolle Definition von Beschleunigung. |
Das ist keine Definition, sondern eine Gleichung. Eine Definition wäre "Beschleunigung := Eigenbeschleunigung", aber davon ist dringend abzuraten, weil der Begriff "Beschleunigung" bereits mit anderer Bedeutung etabliert ist. |
Es ist dringend dazu zu raten, die Begriffe zu etablieren, mit denen sich die Theorie am einfachsten formulieren läßt. In dieser Hinsicht ist Eigenbeschleunigung deutlich überlegen. Moderne Darstellungen verwenden sie deshalb sehr oft. Du kannst gern für immer auf veralteten Begriffen rumreiten, aber helfen wirst du damit niemandem.
|
|
|
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
| Ich Verfasst am: 27. März 2020 11:26 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | Die Behauptung war "F=m*a". Das ist mehr. Genauso wie die Behauptung "Beschleunigung = Eigenbeschleunigung" ist das nicht allgemein gültig. |
Der Satz davor war
| Ich hat Folgendes geschrieben: | | Man sollte einfach mal die richtigen Begriffe aus dem Viererformalismus verwenden: |
Hast du das übersehen?
Diese Aussagen gelten alle im Kontext des Viererformalismus.
Meine Anregung war, diese Bedeutungen der Begriffe auch in der Populärwissenschaft zu bekannt zu machen, weil sie viel tauglicher sind als der ganze Mumpitz mit "immer größere Kraft erforderlich, weil die Trägheit steigt". Der entscheidende Punkt ist, dass das Nichterreichen der Lichtgeschwindigkeit eben kein dynamisches Problem ist, sondern ein kinematisches. Und das sieht man am besten in der kovarianten Formulierung.
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 27. März 2020 11:37 Titel: |
|
|
| Ich hat Folgendes geschrieben: | | Diese Aussagen gelten alle im Kontext des Viererformalismus. |
Was haben Dreierverktoren wie Beschleunigung und Eigenbeschleunigung mit dem Viererformalismus zu tun?
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 27. März 2020 11:41 Titel: |
|
|
| index_razor hat Folgendes geschrieben: | | Es ist dringend dazu zu raten, die Begriffe zu etablieren, mit denen sich die Theorie am einfachsten formulieren läßt. |
Das ist zwar richtig, aber ein anderes Thema. Hier geht es erstmal um die korrekte Verwendung bereits etablierter Begriffe.
|
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 27. März 2020 12:40 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | Ich hat Folgendes geschrieben: | | Diese Aussagen gelten alle im Kontext des Viererformalismus. |
Was haben Dreierverktoren wie Beschleunigung und Eigenbeschleunigung mit dem Viererformalismus zu tun? |
Im Viererformalismus definiert man Dreiervektoren  durch die Bedingung  = 0) , wobei u ein zeitartiger Einheitsvektor ist.
Daran siehst du, daß Eigenbeschleunigung und Viererbeschleunigung eigentlich derselbe Vektor ist. Dasselbe gilt also wegen F=ma auch für Kraft und Viererkraft. Also ist der Viererformalismus alles was man benötigt. Einfacher geht es nicht.
| Zitat: |
Das ist zwar richtig, aber ein anderes Thema. Hier geht es erstmal um die korrekte Verwendung bereits etablierter Begriffe. |
Nein, es ging um den Vorschlag, besser geeignete Begriffe zu etablieren. Du hast das vielleicht falsch verstanden, weil der Doppelpunkt vor dem Gleichheitszeichen fehlte. Ist ja auch unverzeihlich.
|
|
|
DrStupid
Anmeldungsdatum: 07.10.2009
Beiträge: 5041
|
| DrStupid Verfasst am: 27. März 2020 13:43 Titel: |
|
|
| index_razor hat Folgendes geschrieben: | | Daran siehst du, daß Eigenbeschleunigung und Viererbeschleunigung eigentlich derselbe Vektor ist. |
Das hängt davon ab, was "eigentlich derselbe" bedeutet. Dasselbe ist es jedenfalls nicht.
| index_razor hat Folgendes geschrieben: | | Nein, es ging um den Vorschlag, besser geeignete Begriffe zu etablieren. |
Es mag sein, dass das beabsichtigt war, aber herausgekommen ist etwas anderes - nämlich der Vorschlag, bereits etablierte Begriffe umzudefinieren. Das trägt nicht zum besseren Verständnis, sondern - ganz im Gegenteil - zur Verwirrung bei. Wer Viererbeschleunigung meint sollte auch Viererbeschleunigung schreiben.
Wenn die korrekte Bezeichnung "Viererbeschleunigung" auf Dauer zu langatmig wird, dann ist es prinzipiell denkbar (wenn auch nicht empfehlenswert), stattdessen den Begriff "Beschleunigung" als eine Art Laborjargon zu missbrauchen. Das setzt aber voraus, dass das klar kommuniziert wird (wofür kryptische Formulierungen wie "Beschleunigung = Eigenbeschleunigung" ganz sicher nicht ausreichen) und die Verwendung des Begriffes in seiner ursprünglichen Bedeutung ausgeschlossen ist (wovon ich in einem Physikforum eher nicht ausgehe).
Das ist hier aber gar nicht nötig. Was spricht dagegen zu schreiben, dass für die Viererkraft F, die invariante Masse m und die Viererbeschleunigung a die Beziehung F=m*a gilt? Wozu muss da da mit Begriffen handtieren, die etwas anderes bedeuten?
|
|
|
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 829
|
| Qubit Verfasst am: 27. März 2020 13:47 Titel: |
|
|
| index_razor hat Folgendes geschrieben: |
Im Viererformalismus definiert man Dreiervektoren durch die Bedingung , wobei u ein zeitartiger Einheitsvektor ist.
Daran siehst du, daß Eigenbeschleunigung und Viererbeschleunigung eigentlich derselbe Vektor ist. Dasselbe gilt also wegen F=ma auch für Kraft und Viererkraft. Also ist der Viererformalismus alles was man benötigt. Einfacher geht es nicht.
|
Ist es nicht eher so, dass nur die invariante Norm der Viererbeschleunigung dann mit der Eigenbeschleunigung übereinstimmt?
Eigenbeschleunigung und die darauf definierte Kraft sind ja eben nicht lorentzinvariant.
|
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 27. März 2020 14:35 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: | | Daran siehst du, daß Eigenbeschleunigung und Viererbeschleunigung eigentlich derselbe Vektor ist. |
Das hängt davon ab, was "eigentlich derselbe" bedeutet. Dasselbe ist es jedenfalls nicht.
|
Doch, genau derselbe, wie in "Gleichheit im Vektorraum" bzw.  .
Dreiervektoren sind einfach die Vektoren aus dem dreidimensionalen orthogonalen Komplement der Vierergeschwindigkeit 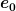 . Darin besteht ja gerade die Vereinfachung durch den Viererformalismus: man benötigt nur einen Minkowskiraum. Alle Dreiervektoren sind schon drin.
| Zitat: |
| index_razor hat Folgendes geschrieben: | | Nein, es ging um den Vorschlag, besser geeignete Begriffe zu etablieren. |
Es mag sein, dass das beabsichtigt war, aber herausgekommen ist etwas anderes - nämlich der Vorschlag, bereits etablierte Begriffe umzudefinieren.
|
Nein, es wurde nur vorgeschlagen, die Begriffe des Viererformalismus einzuführen. Es hat niemand was dagegen, die Viererbeschleunigung "Viererbeschleunigung" zu nennen. Ich würde dann allerdings auch konsequent von "Dreierbeschleunigung" reden.
Je vertrauter man mit dem Viererformalismus ist, desto natürlicher ist es, den Begriff "Beschleunigung" auf die Viererbeschleunigung zu beziehen. Das Wort "Masse" hat dieselbe Entwicklung durchgemacht. "Ruhemasse" sagt heute kaum noch jemand. Selbst "invariante Masse" scheint ein bißchen aus der Mode zu kommen, und mit "Masse" ist fast immer einfach  gemeint.
| Zitat: |
Wenn die korrekte Bezeichnung "Viererbeschleunigung" auf Dauer zu langatmig wird, dann ist es prinzipiell denkbar (wenn auch nicht empfehlenswert), stattdessen den Begriff "Beschleunigung" als eine Art Laborjargon zu missbrauchen.
|
Da muß man nichts mißbrauchen. Man sagt einfach klipp und klar, "Wenn ich im folgenden von 'Beschleunigung' rede, dann meine ich  . Für  sage ich hingegen '3er-Beschleunigung'."
Das hat den klaren Vorteil, daß man für den nützlicheren Begriff, den man, um möglichst verständliche Darstellung der Theorie bemüht, ohnehin die ganze Zeit verwendet, weniger Umstände machen muß.
Du solltest dir einfach ein entspannteres Verhältnis zu terminologischen Fragen zulegen. Auf "etablierten" Definitionen zu beharren und damit alles umständlicher zu machen, hilft, wie gesagt, niemandem.
| Zitat: |
Das setzt aber voraus, dass das klar kommuniziert wird (wofür kryptische Formulierungen wie "Beschleunigung = Eigenbeschleunigung" ganz sicher nicht ausreichen)
|
Es war sicher nur als knapper Hinweis auf geeignetere Konzepte gedacht, nicht als didaktisch wertvolle Abhandlung über die Relativitätstheorie. Aber im Prinzip stimme ich hier natürlich zu. Vielleicht haben wir ja in der Zwischenzeit sogar noch ein bißchen mehr zur Klarheit beigetragen. Ansonsten kann man in einem Forum bei Unklarheit ja auch immer nachfragen.
| Zitat: |
Das ist hier aber gar nicht nötig. Was spricht dagegen zu schreiben, dass für die Viererkraft F, die invariante Masse m und die Viererbeschleunigung a die Beziehung F=m*a gilt? Wozu muss da da mit Begriffen handtieren, die etwas anderes bedeuten? |
Was die Begriffe bedeuten, bestimmen in erster Linie die, die sie verwenden (müssen). Das richtet sich ausschließlich nach praktischen Gesichtspunkten. Die praktischste Bedeutung ist auch die, die man in der Didaktik einführen sollte. Denn was hat man davon, wenn man den ganzen Kram jahrelang studiert und dann doch nicht versteht, wovon die Rede ist?
Jeder vernünftige Mensch gibt dir natürlich recht, daß man dabei vor allem Mißverständnisse vermeiden muß. Wenn jemand nur 3er-Beschleunigungen kennt, sollte man nicht einfach ohne Vorwarnungen anfangen mit "Beschleunigung" die Vierebeschleunigung zu bezeichnen. Und eine Vorwarnung auf den "Viererformalismus" wurde ja deswegen auch extra gegeben.
|
|
|
Nils Hoppenstedt
Anmeldungsdatum: 08.01.2020
Beiträge: 2019
|
| Nils Hoppenstedt Verfasst am: 27. März 2020 14:35 Titel: |
|
|
|
Ich kenne das auch nur so, dass die Eigenbeschleunigung die Dreierbeschleunigung im momentanen Ruhesystem ist, während die Vierbeschleunigung die Ableitung der Vierergeschwindigkeitkeit nach der Eigenzeit bedeutet.
|
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 27. März 2020 14:53 Titel: |
|
|
| Qubit hat Folgendes geschrieben: | | index_razor hat Folgendes geschrieben: |
Im Viererformalismus definiert man Dreiervektoren durch die Bedingung , wobei u ein zeitartiger Einheitsvektor ist.
Daran siehst du, daß Eigenbeschleunigung und Viererbeschleunigung eigentlich derselbe Vektor ist. Dasselbe gilt also wegen F=ma auch für Kraft und Viererkraft. Also ist der Viererformalismus alles was man benötigt. Einfacher geht es nicht.
|
Ist es nicht eher so, dass nur die invariante Norm der Viererbeschleunigung dann mit der Eigenbeschleunigung übereinstimmt?
Eigenbeschleunigung und die darauf definierte Kraft sind ja eben nicht lorentzinvariant. |
Die Frage demonstriert ganz gut, welche Art von Komplikation man im Viererformalismus ohne Aufwand vermeiden kann.
Deine Überlegung geht wahrscheinlich so: Im Ruhesystem des Teilchens ist die Viererbeschleunigung ) und  ist der Dreiervektor der Eigenbeschleunigung, also irgendwie etwas anderes als . Das ist aber nur eine etwas unelegante Formulierung von
mit der Zusatzbedingung  = 0) .
Da die Bedingung =0) basisunabhängig ist, ist auch die Eigenbeschleunigung -- so wie eigentlich alles in der SRT, was mit "Eigen-" anfängt -- eine Lorentzinvariante.
|
|
|
Ich
Anmeldungsdatum: 11.05.2006
Beiträge: 913
Wohnort: Mintraching
|
| Ich Verfasst am: 27. März 2020 15:00 Titel: |
|
|
| DrStupid hat Folgendes geschrieben: | | Ich hat Folgendes geschrieben: | | Diese Aussagen gelten alle im Kontext des Viererformalismus. |
Was haben Dreierverktoren wie Beschleunigung und Eigenbeschleunigung mit dem Viererformalismus zu tun? |
Der Begriff "Beschleunigung" meint im Viererformalismus natürlich die Viererbeschleunigung. Deren Betrag ist auch der Betrag der Eigenbeschleunigung. Dass der Vektor auch Eigenbeschleunigung genannt würde war eine Verwechslung meinerseits.
|
|
|
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
| index_razor Verfasst am: 27. März 2020 15:09 Titel: |
|
|
| Ich hat Folgendes geschrieben: | | Dass der Vektor auch Eigenbeschleunigung genannt würde war eine Verwechslung meinerseits. |
Ich glaube die eigentliche Verwechslung besteht, wie so oft, darin, daß der 3er-Vektor der Eigenbeschleunigung mit seinen drei Komponenten ) bzgl. eines momentanen Ruhesystems identifiziert wird.
Ein Komponententripel ist natürlich nicht dasselbe wie ein Vierervektor. Aber der Vektor selbst, also  , ist derselbe wie die Viererbeschleunigung.
|
|
|
Qubit
Anmeldungsdatum: 17.10.2019
Beiträge: 829
|
| Qubit Verfasst am: 27. März 2020 15:35 Titel: |
|
|
| index_razor hat Folgendes geschrieben: |
Ich glaube die eigentliche Verwechslung besteht, wie so oft, darin, daß der 3er-Vektor der Eigenbeschleunigung mit seinen drei Komponenten bzgl. eines momentanen Ruhesystems identifiziert wird.
|
Okay, danke, deine Ausführungen machen es jetzt verständlicher.
Kannst du vielleicht mal den einfachen Fall eines homogenen externen Kraftfeldes in zwei Systemen (inertial, beschleunigt) mit den Komponenten der Eigenkraft/beschleunigung und Transformationen aufschreiben?
|
|
|
|
Registrieren
Login
FAQ
Suchen
