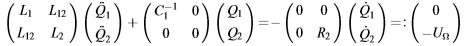inkognito89
Anmeldungsdatum: 15.11.2019
Beiträge: 12
|
 inkognito89 Verfasst am: 19. Nov 2019 18:53 Titel: Induktiv gekoppelter Schwingkreis inkognito89 Verfasst am: 19. Nov 2019 18:53 Titel: Induktiv gekoppelter Schwingkreis |
 |
|
Meine Frage:
Guten Abend liebe Mitglieder.
Ich soll einen induktiv gekoppelten Schwingkreis mithilfe von Runge Kutta numerisch lösen. Siehe Datei.
Meine Ideen:
Siehe Pythondatei.
import numpy as np
from scipy import integrate
from scipy.integrate import ode
import sympy
import matplotlib.pylab as plt
import math
# Definiere SymPy symbols für die Variablen und die Funktionen
t, l_1, l_2, l_12, c_1, r_2 = sympy.symbols("t, l_1, l_2, l_12, c_1, r_2")
q1, q2 = sympy.symbols("q1, q2", cls=sympy.Function)
#ODE´s für primärer und sekundärer Schwingkreis
ode1 = sympy.Eq(l_1 * q1(t).diff(t,t) + l_12 * q2(t).diff(t,t) + q1(t)/c_1)
ode2 = sympy.Eq(l_12 * q1(t).diff(t,t) + l_2 *q2(t).diff(t,t) + r_2 * q2(t).diff(t))
# Jetzt sind ode1 und ode2 sympy expressions für die Differentialgleichungen 2. Ordnung (noch nicht in Form für ODE solvers)
# Umschreiben in ein System von DGL´s 1. Ordnung
# z_1 = q1(t); z_2 = q1'(t); z_3 = q2(t), z_4 = q2'(t)
z_1, z_2, z_3, z_4 = sympy.symbols("z_1, z_2, z_3, z_4", cls=sympy.Function)
varchange = {q1(t).diff(t,t):
z_2(t).diff(t),
q1(t): z_1(t),
q2(t).diff(t,t):
z_4(t).diff(t),
q2(t): z_3(t)}
ode1_vc = ode1.subs(varchange)
ode2_vc = ode2.subs(varchange)
# wir müssen noch zwei weitere ODE's einführen: z_1'(t) und z_3'(t)
ode3 = z_1(t).diff(t) - z_2(t)
ode4 = z_3(t).diff(t) - z_4(t)
# An dieser Stelle haben wir 4 gekoppelte DGL's 1.Ordnung
# Nun müssen wir die Ableitungen dieser Funktionen lösen um die ODE's in Standardform zu erhalten (benutze sympy.solve)
z = sympy.Matrix([z_1(t), z_2(t), z_3(t), z_4(t)])
vcsol = sympy.solve((ode1_vc, ode2_vc, ode3, ode4), z.diff(t), dict=True)
f = z.diff(t).subs(vcsol[0])
# Nun ist f sympy expression für die ODE Funktion f(t,z(t))
# Wir könnten die ODE mit sympy.Eq(z.diff(t), f) darstellen, aber das Ergebnis wäre sehr lange
# Main purpose: Konstruiere f an dieser Stelle um es in eine NumPy-aware Funktion zu konvertieren, welche mit integrate.odeint oder integrate.ode genutzt werden kann
# Konstruiere so eine Funktion mit sympy.lambdify
k = 0.5 # Kopplungsfaktor \in (0, 1) Induktionen der Spulen müssen sehr weit voneinander entfernt sein => l1 ist VIEL kleiner als l2
params = {l_1: 5, l_2: 1000, l_12: 12, c_1: 2, r_2: 10} # Werte der Parameter Anmerkung: es handelt sich noch um fiktive Werte
_f_np = sympy.lambdify((t, z), f.subs(params), 'numpy')
f_np = lambda _t, _z, *args: _f_np(_t, _z)
# benutze jac für Jacobianmatrix
jac = sympy.Matrix([[fj.diff(zi) for zi in z] for fj in f])
_jac_np = sympy.lambdify((t, z), jac.subs(params), 'numpy')
jac_np = lambda _t, _z, *args: _jac_np(_t, _z)
# an dieser Stelle haben wir spezielle Werte der Systemparameter substituiert bevor wir sympy.lambdify aufrufen.
# Dämpfung des Systems
u_c = 2/params[c_1]
omega = params[l_1]/params[l_2]
# vorerst u_omega = 2 !
z0 = [2.0, 0.0, 0.0, 0.0]
print(z0)
tt = np.linspace(0, 1000, 1000)
r = integrate.ode(f_np,jac_np).set_initial_value(z0, tt[0])
dt = tt[1] - tt[2]
zz = np.zeros((len(tt), len(z0)))
gedaempft = np.zeros((len(tt)))
idx = 0
# Grenzfall: aperiodischer Grenzfall omega = delta
daempfungsfaktor = params[r_2 ]/ (2 * params[l_12])
while r.successful() and idx<1000:
zz[idx,  = r.y = r.y
r.integrate(r.t + dt)
# gedaempft[idx] = -u_c/params[l_12] * idx * math.exp(-omega*idx)
# aperiodischer Grenzfall i(t) = -U_c_0/L * t * e^{-omega_0 * t}
gedaempft[idx] = zz[idx, 3] * math.exp((-params[r_2]*idx)/(2*params[l_12]))
# die Lösung der ODE's ist nun in dem Array zz gepeichert, welches die Größe (1000, 4) hat.
idx += 1
q1_np, q1_dot_np, q2_np, q2_dot_np = zz[:,0], zz[:,1], zz[:,2], zz[:,3]
x1 = q1_np
x2 = q1_dot_np
x3 = -q2_np
x4 = -q2_dot_np
# Plot
fig, (ax1, ax2, ax3, ax4, ax5) = plt.subplots(5, 1, sharex=True)
ax1.plot(tt,x1)
ax1.set_ylabel('Q_1')
ax2.plot(tt, x2)
ax2.set_ylabel('Q_1^`')
ax3.plot(tt,x3)
ax3.set_ylabel('Q_2')
ax4.plot(tt,x4)
ax4.set_ylabel('Q_2^´')
ax5.plot(tt,gedaempft)
ax5.set_ylabel('gedämpft')
ax5.set_xlabel('time t')
plt.show()
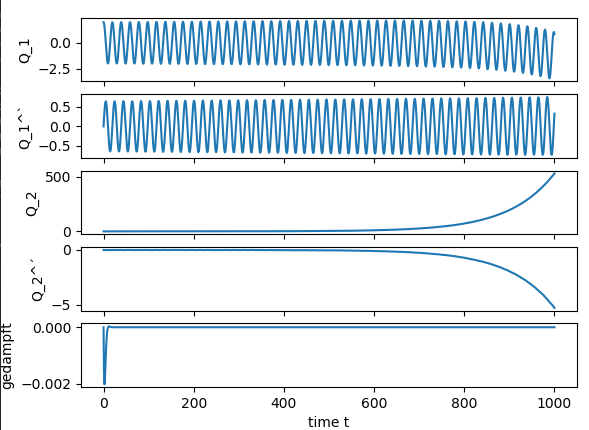
Leider glaube ich, dass das Ergebnis nicht realistisch aussieht. Deshalb würde ich euch gerne um eure Meinung/Hilfe bitten.
Danke!
| Beschreibung: |
|
| Dateigröße: |
57.8 KB |
| Angeschaut: |
931 mal |
|
| Beschreibung: |
|
| Dateigröße: |
7.01 KB |
| Angeschaut: |
931 mal |
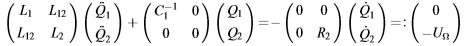
|
| Beschreibung: |
|
| Dateigröße: |
3.17 KB |
| Angeschaut: |
931 mal |
|
|
|
















 = r.y
= r.y