| Autor |
Nachricht |
Lopezoli
Anmeldungsdatum: 10.12.2018
Beiträge: 1
|
 Lopezoli Verfasst am: 10. Dez 2018 12:26 Titel: Seilzugänderung aufgrund von Temperaturänderung Lopezoli Verfasst am: 10. Dez 2018 12:26 Titel: Seilzugänderung aufgrund von Temperaturänderung |
 |
|
Meine Frage:
Gegeben ist ein Seil (Durchmesser, Material), welches zwischen 2 Masten mit Abstand L befestigt ist und mit einer definierten Kraft F gespannt wird.
Aufgrund von Temperaturänderung (dT) erfährt das Seil eine Längenänderung (dL).
Gesucht ist die Funktion für die Zugkraft in Abhängigkeit von dT.
Meine Ideen:
Formel für Längenänderung des Seil bekannt, jedoch fehlt Verbindung zur Zugkraftänderung. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 10. Dez 2018 14:00 Titel: Myon Verfasst am: 10. Dez 2018 14:00 Titel: |
 |
|
Man kann ausrechnen, wie sich die Kraft ändert bei einer Temperaturänderung, dF/dT. Damit kann man dann auch, falls tatsächlich gewünscht, die Kraft in der Form angeben
=F_0+\frac{\dd F}{\dd T}\Delta T)
Bei einer Temperaturänderung ändert sich die Länge 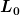 des entspannten Seils. Also zuerst F in Abhängigkeit von L und L0 schreiben, dann ergibt sich dF/dT aus des entspannten Seils. Also zuerst F in Abhängigkeit von L und L0 schreiben, dann ergibt sich dF/dT aus

Ich gehe davon aus, dass der Elastizitätsmodul und der Längenausdehnungskoeffizient des Materials bekannt sind. |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 10. Dez 2018 14:58 Titel: Mathefix Verfasst am: 10. Dez 2018 14:58 Titel: |
 |
|
Längenänderung

<br />
)

)
oder näherungsweise

Seilkraft
Die Seilkraft wird bestimmt durch:
a) Gewichtskraft
b) Spannkraft
Die Bestimmung der Seilkraft ist kompliziert.
Durch die Längenänderung wird die Gewichtskraft nicht geändert; es ändert sich die Länge des Seils und damit die Form der Seillinie und damit die Seilkraft.
Ist mir im Augenblick zu aufwändig.[l
Zuletzt bearbeitet von Mathefix am 10. Dez 2018 16:02, insgesamt 2-mal bearbeitet |
|
 |
Lopezoli2
Gast
|
 Lopezoli2 Verfasst am: 10. Dez 2018 15:12 Titel: Vorschlag Lopezoli2 Verfasst am: 10. Dez 2018 15:12 Titel: Vorschlag |
 |
|
Hi
Ich hab mal weitergeschaut und bin auf folgendes gekommen:
Längenänderung aufgrund von Temperaturänderung
)
Längenänderung aufgrund von Zugkraftänderung
*L}{E*A})
Indem ich nun die 2 Formeln gleichsetze, kann ich das gesuchte Fx(Tx) ausrechnen oder?
Oder sind die Formeln so nicht kompatibel? |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 10. Dez 2018 15:25 Titel: Re: Vorschlag Mathefix Verfasst am: 10. Dez 2018 15:25 Titel: Re: Vorschlag |
 |
|
| Lopezoli2 hat Folgendes geschrieben: | Hi
Ich hab mal weitergeschaut und bin auf folgendes gekommen:
Längenänderung aufgrund von Temperaturänderung
)
Längenänderung aufgrund von Zugkraftänderung
*L}{E*A})
Indem ich nun die 2 Formeln gleichsetze, kann ich das gesuchte Fx(Tx) ausrechnen oder?
Oder sind die Formeln so nicht kompatibel? |
Bei Deinem Ansatz (Hooke´sches Gesetz) würde F_x mit wachsender Temperaturdifferenz und damit Längenänderung steigen. Die Längenänderung wird aber nicht durch eine Kraft erzeugt.
Bei Deiner Rechnung ist F_x die Kraft, welche die gleiche Längenänderung des Seils durch Temperaturerhöhung erfährt.
Wie ich in meinem Beitrag erwähnte, muss man ceteris paribus die Seillänge in einem vorgespannten Seil vegrössern und die dann vorhandene Seilkraft bestimmen - sehr kompliziert. |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 10. Dez 2018 17:58 Titel: Myon Verfasst am: 10. Dez 2018 17:58 Titel: |
 |
|
Wenn zu Beginn die Seilkraft gleich F ist, dann gilt (vom Einfluss einer Gewichtskraft wird dabei abgesehen)
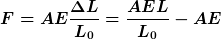
Bei einer Temperaturänderung um 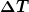 ändert die Länge des entspannten Seiles um ändert die Länge des entspannten Seiles um

Dies bewirkt eine Änderung der Seilkraft um
\Delta T\approx -\alpha AE\Delta T) |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 10. Dez 2018 19:15 Titel: Mathefix Verfasst am: 10. Dez 2018 19:15 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | Wenn zu Beginn die Seilkraft gleich F ist, dann gilt (vom Einfluss einer Gewichtskraft wird dabei abgesehen)
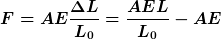
Bei einer Temperaturänderung um 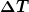 ändert die Länge des entspannten Seiles um ändert die Länge des entspannten Seiles um

Dies bewirkt eine Änderung der Seilkraft um
 |
Hmm, ich weiss nicht, ob man das so machen kann. Vllt. als (grobe ?) Näherungslösung.
Du betrachtest ersatzweise einen einseitig fixierten horizontalen, vorgespannten starren Stab und vernachlässigst (was ok wäre) die Durchbiegung durch Eigengewicht.
Die Vorspannkraft wird reduziert um die Kraft, die durch die Längenänderung entsteht. Nämlich um
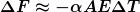 |
|
 |
Myon
Anmeldungsdatum: 04.12.2013
Beiträge: 5955
|
 Myon Verfasst am: 10. Dez 2018 19:32 Titel: Myon Verfasst am: 10. Dez 2018 19:32 Titel: |
 |
|
Die Ableitung
)
ist genau und keine Näherung. Für kleine Temperaturänderungen gilt also sicher \Delta T) . Das Hookesche Gesetz gilt ohnehin nur für einen Bereich, in dem die Seilkraft sich linear zur Längenänderung verhält. . Das Hookesche Gesetz gilt ohnehin nur für einen Bereich, in dem die Seilkraft sich linear zur Längenänderung verhält. |
|
 |
Mathefix
Anmeldungsdatum: 05.08.2015
Beiträge: 5918
Wohnort: jwd
|
 Mathefix Verfasst am: 10. Dez 2018 20:04 Titel: Mathefix Verfasst am: 10. Dez 2018 20:04 Titel: |
 |
|
| Myon hat Folgendes geschrieben: | Die Ableitung
)
ist genau und keine Näherung. Für kleine Temperaturänderungen gilt also sicher \Delta T) . Das Hookesche Gesetz gilt ohnehin nur für einen Bereich, in dem die Seilkraft sich linear zur Längenänderung verhält. . Das Hookesche Gesetz gilt ohnehin nur für einen Bereich, in dem die Seilkraft sich linear zur Längenänderung verhält. |
Innerhalb Deines Ansatzes hast Du mathematisch ja recht. Mit Näherungslösung habe ich den ganzen Ansatz gemeint.
Mit einem gespannten Seil hat das wenig zu tun. Die Spannkraft und damit die Längenänderung nimmt bei einem Seil überporportional zu bw. ab.
Seis´s drum, immerhin eine Grössenordnung.
Gruss
Jörg |
|
 |
|















