| Autor |
Nachricht |
HansWerner
Anmeldungsdatum: 01.10.2017
Beiträge: 8
|
 HansWerner Verfasst am: 01. Okt 2017 14:25 Titel: SU(3)-Farb-Symmetrie HansWerner Verfasst am: 01. Okt 2017 14:25 Titel: SU(3)-Farb-Symmetrie |
 |
|
Meine Frage:
Hallo,
ich hätte da eine konzeptionelle Frage zur ) -Farbladungserhaltung bei Quarks. Noether-Theorem stellt sicher, dass zur jeder Symmetrie eine Invariante existiert, hier also korrespondiert offensichlich die -Farbladungserhaltung bei Quarks. Noether-Theorem stellt sicher, dass zur jeder Symmetrie eine Invariante existiert, hier also korrespondiert offensichlich die _C) -Symmetrie zur Farbladung, wobei mir schwer fällt mathematisch diese Farbladungserhaltung im Farbraum vorzustellen. Unten habe ich meine Überlegungen zur Isospin-Erhaltung im Proton-Neutron-Raum (sind diese richtig?) auf den 3d Raum zu erweitern, allerdings weiß ich nicht ob dies alles korrekt sei: -Symmetrie zur Farbladung, wobei mir schwer fällt mathematisch diese Farbladungserhaltung im Farbraum vorzustellen. Unten habe ich meine Überlegungen zur Isospin-Erhaltung im Proton-Neutron-Raum (sind diese richtig?) auf den 3d Raum zu erweitern, allerdings weiß ich nicht ob dies alles korrekt sei:
Meine Ideen:
Betrachten wir zunächst die Essenz der ) -Symmetrie beim Isospin -Symmetrie beim Isospin 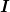 , welche (nach Noether) die Erhaltung einer Größe - hier der Quantenzahl , welche (nach Noether) die Erhaltung einer Größe - hier der Quantenzahl  unter unter ) -Rotationen - garantiert. -Rotationen - garantiert.
Wenn ich mich nicht täusche wird dies mathematisch wie folgt begründet:
Der 2d Isospin-Raum (noch ohne Kopplungen mit anderen Systemen) wird aufgespannt die die Proton-Neutron-Basis:
 , ,
sodass jeder beliebiger Vektor in Isospin-Raum gerade der Linearkombination

entspricht. Weiterhin gilt für den Operator 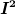 : :
\left| 1/2, +1/2\right> = \hbar^23/2\left| 1/2, +1/2\right> ) , sowie , sowie
\left| 1/2, -1/2\right> = \hbar^23/2\left| 1/2, -1/2\right> ) . .
Da also Proton und Neutron dieselbe Quantenzahl  besitzen, gilt dies für beliebiges besitzen, gilt dies für beliebiges  an damit beilibige an damit beilibige ) -Drehung davon. -Drehung davon.
Dies ist , was ich unter ) -Isospin-Symmetrie verstehe. Zunächst einmal: ist diese Anschauung jedenfalls korrekt? -Isospin-Symmetrie verstehe. Zunächst einmal: ist diese Anschauung jedenfalls korrekt?
Nun kommen wir zurück zu ) -Farbsymmetrie, wobei ich im folgenden versuchen werde analog zum oberen Fall zu überlegen. -Farbsymmetrie, wobei ich im folgenden versuchen werde analog zum oberen Fall zu überlegen.
Wir hätten diesmal den 3dimnl Farbraum aufgespannt von
 . .
Meine Frage ist:
Was ist die Invariante vom beliebigen Vektor  aus dem Farbraum? aus dem Farbraum?
Wenn ich naiv die Isospin-Überlegungen von oben heranziehe, so könnte ich den Farbraum als Triplett, das durch eine Quantenzahl  charakterisiert ist deuten, die gerade meine charakterisiert ist deuten, die gerade meine _C) -Invariante sein wird. So hätte ich dann für die rgb-Basis die Darstellungen -Invariante sein wird. So hätte ich dann für die rgb-Basis die Darstellungen
 . .
Dies Vorstellung scheint mir jedoch ZU naiv zu sein.
Wie ist denn (falls meine Überlegungen falsch sein sollten) die Farb-Symmetrie (insb. mathem.) vorzustellen. Banale Frage wäre zunächst was wird da erhalten (Farbladung?) und wie wird die Quantenzahl beschrieben? (muss gestehen, dass ich nirgendwo die explizite Darstellung einer "Farbladungs"-Quantenzahl findn konnte :/ |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 01. Okt 2017 15:20 Titel: TomS Verfasst am: 01. Okt 2017 15:20 Titel: |
 |
|
Zunächst mal solltest du von SU(3) sprechen, nicht von SO(3).
Dann musst du zwischen Rotation und Symmetrie unterscheiden. Die Rotation hast du im wesentlichen richtig beschrieben. Eine Symmetrie liegt jedoch nur dann vor, wenn der Hamiltonoperator invariant unter dieser Rotation ist. Konkret: Isospininvarianz liegt deshalb (näherungsweise) vor, weil Zustände mit +1/2 und -1/2 wie z.B. Proton und Neutron (näherungsweise) identische Masse haben.
Die Invarianten sind die sogenannten Casimir-Operatoren der jeweiligen Gruppe. Der Rang der Gruppe liefert die Anzahl der Casimir-Operatoren. Im Falle von SU(N) ist der Rang gerade N-2.
Algebraisch benötigst du zunächst die Generatoren, d.h. für die SU(2) die Pauli- und für die SU(3) die Gell-Mann-Matrizen. Aus diesen folgen die Casimir-Operatoren.
Für SU(2) entspricht der erste Casimir-Operator gerade dem Gesamtdrehimpuls.
Für die SU(3) ist das zunächst komplizierter. Im Falle der SU(3) für Color reduziert sich die Problematik jedoch, weil alle physikalischen Zustände Color-Singulets sein müssen (was nicht aus der Algebra folgt sondern eine davon unabhängige Zusatzbedingung aus der Dynamik der QCD ist). D.h. dass die Eigenwerte für alle acht Operatoren verschwinden.

https://en.m.wikipedia.org/wiki/Clebsch–Gordan_coefficients_for_SU(3)
Zuletzt bearbeitet von TomS am 01. Okt 2017 17:02, insgesamt 2-mal bearbeitet |
|
 |
HansWerner
Anmeldungsdatum: 01.10.2017
Beiträge: 8
|
 HansWerner Verfasst am: 01. Okt 2017 16:58 Titel: HansWerner Verfasst am: 01. Okt 2017 16:58 Titel: |
 |
|
Hi Tom,
danke für die schnelle und aufschlussreiche Antwort. Jedoch hätte ich ein Paar Verständnisfragen dazu:
Wenn ich den Gedankengang richtig verstanden habe, dann sind die Casimir-Operatoren als Invarianten gerade diejenigen, die mit den Hamilton-Operator vertauschen. Sind dann also ihre Eigenwerte sozusagen die korrespondierenden „skalaren“ (zu ihren jeweiligen Casimir-Ops) Invarianten? Wenn ich nämlich wieder auf das Beispiel der Isospin-Symmetrie zurückkomme, dann ist 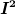 mein einziger Casimir-Operator mit EW 1/2, nicht? mein einziger Casimir-Operator mit EW 1/2, nicht?
Nebenbei bemerkt, meintest du mit Anzahl der Casimir-Operatoren für SU(N) nicht eigentlich N-1? SU(2) bei Isospin hat doch gerade mit 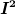 einen Casimir-Op.? einen Casimir-Op.?
Und zu deinem letzten Paragraph: Also physikalisch bedingt treten wie du es richtig gesagt hast, nur Singuletts auf, müssen wir nach obigen Überlegungen bloß zur Kenntnis nehmen, dass die EW von den beiden (3-1, falls es doch N-1 gilt) Null sind? Aber diese Singuletts sind bereit geeignet gekoppelte Zustände von r,g und b,oder?Aber verlässt man dadurch nicht den 3d Farbraum  auf dem auf dem _C) wirkt? Bzw wie ändert sich der Farbraum durch die Kopplungen, die sicherstellen, dass man einen Sigulett hat? wirkt? Bzw wie ändert sich der Farbraum durch die Kopplungen, die sicherstellen, dass man einen Sigulett hat? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 01. Okt 2017 17:09 Titel: TomS Verfasst am: 01. Okt 2017 17:09 Titel: |
 |
|
Zunächst mal ja, du hast recht mit N-1, N-2 ist falsch, ich korrigiere das.
Bzgl. der Casimir-Operatoren: zunächst mal sind sie dadurch definiert, dass sie alle gleichzeitig proportional zur Eins sind. Dass sie mit dem Hamilton-Operator vertauschen gilt wieder nur für den Fall dass eine Symmetrie vorliegt. L^2 ist z.B. immer ein Casimir-Operator der SU(2), aber für nicht rotationsinvariante Potentiale keine Erhaltungsgröße.
Zu deiner letzten Frage: ja, man muss die einzelnen Farben der fundamentalen Darstellung (der Quarks) geeignet koppeln. Überleg' dir das mal für zwei Spin 1/2 Teilchen; das Singulett ist ja gerade S = 1. Das Triplett S = 1 scheidet komplett aus.
Du kannst dir die beiden Casimir-Operatoren der SU(3) natürlich trotzdem anschauen (siehe der verlinkte Artikel). Sie sind für Singuletts natürlich wieder Null (siehe meine o.g. Gleichung)
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 01. Okt 2017 17:30 Titel: index_razor Verfasst am: 01. Okt 2017 17:30 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Bzgl. der Casimir-Operatoren: zunächst mal sind sie dadurch definiert, dass sie alle gleichzeitig proportional zur Eins sind. Dass sie mit dem Hamilton-Operator vertauschen gilt wieder nur für den Fall dass eine Symmetrie vorliegt. L^2 ist z.B. immer ein Casimir-Operator der SU(2), aber für nicht rotationsinvariante Potentiale keine Erhaltungsgröße.
|
Dann stimmt was mit deiner Definition nicht. Wenn sie proportional zu Eins sind, vertauschen sie mit allen Operatoren.
Daß die Darstellung eines Casimir-Operators ~1 ist, kennzeichnet meines Wissens gerade irreduzible Darstellungen der Gruppe. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 01. Okt 2017 17:57 Titel: TomS Verfasst am: 01. Okt 2017 17:57 Titel: |
 |
|
Die Casimir-Operatoren einer Algebra vertauschen mit allen Elementen dieser Algebra, z.B. hier su(N), jedoch nicht zwingend mit allen Operatoren auf dem Hilbertraum.
Z.B. vertauscht L^2 mit allen K_i, jedoch nicht mit beliebigen H.
Das "proportional zur Eins" bezieht sich tatsächlich nur auf die Algebra, nicht auf den Hilbertraum. Sorry, das hatte ich recht verwirrend beschrieben.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 01. Okt 2017 18:10 Titel: index_razor Verfasst am: 01. Okt 2017 18:10 Titel: |
 |
|
| TomS hat Folgendes geschrieben: |
Das "proportional zur Eins" bezieht sich tatsächlich nur auf die Algebra, nicht auf den Hilbertraum. Sorry, das hatte ich recht verwirrend beschrieben. |
Was meinst du damit? Casimir-Operatoren sind nicht notwendigerweise proportional zum Einselement der Algebra. Sie vertauschen, wie du sagst, mit allen Elementen der Algebra. Deshalb sind sie, nach Schurs Lemma, proportional zur Eins auf jeder irreduziblen Darstellung der Algebra. Mehr kann man, denke ich, im allgemeinen nicht sagen. |
|
 |
HansWerner
Anmeldungsdatum: 01.10.2017
Beiträge: 8
|
 HansWerner Verfasst am: 01. Okt 2017 22:46 Titel: HansWerner Verfasst am: 01. Okt 2017 22:46 Titel: |
 |
|
@Tom:
Hätte da noch ein Paar Fragen zu deinem 2. Post:
| TomS hat Folgendes geschrieben: | | Zu deiner letzten Frage: ja, man muss die einzelnen Farben der fundamentalen Darstellung (der Quarks) geeignet koppeln. Überleg' dir das mal für zwei Spin 1/2 Teilchen; das Singulett ist ja gerade S = 1. Das Triplett S = 1 scheidet komplett aus. |
Wenn ich jetzt (mal wieder) die Analoge zur Wirkung vom Casimir-Operator 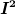 auf gekoppelte Zustände im Isospin-Raum aufgreife, dann verfahre ich ja nach folgendem Schema: auf gekoppelte Zustände im Isospin-Raum aufgreife, dann verfahre ich ja nach folgendem Schema:

mit geeigneten CG-Koeffizieten a, b, c,d. Dabei liefern gewisse Linearkombinationen von  Eigenwertgleichungen der Form Eigenwertgleichungen der Form
= K \sum\limits_{m_1, M_2} c_{m_1, m_2} \left| 1/2, m_1 \right> \otimes \left| 1/2, m_2 \right> )
mit  ) . Dabei entscheidet wieder der Eigenwertentartungsgrad ob seinem zugehörigen Eigenvektoren Singulett, Dublett, Triplett et cetera bilden, oder hab ich das total missverstanden? . Dabei entscheidet wieder der Eigenwertentartungsgrad ob seinem zugehörigen Eigenvektoren Singulett, Dublett, Triplett et cetera bilden, oder hab ich das total missverstanden?
Kann ich dieses Kopplungsprinzip nun auf Quarks aus dem Farbraum bedenkenlos übertragen, wobei diesmal ich natürlich andere (zwei genau genommen) Casimir-Operatoren nach dem gleichen Muster wie oben Linearkombinationen von gekoppelten Quarkzuständen wirken lasse, mit Berücksichtigung (aus rein empirischen Gründen), dass jeder Eigenzustand nicht entartet ist (also Singulett (S=0) = Eigenraum eindimensional)?
Hmmm, was mir noch etwas abstrus bei Farbsymmetrie erscheint, ist dass wenn wir zwei mit H vertauschende Casimir-Op. haben, dann hätten wir ja zwei Erhaltungsgrößen, wieso spricht man dann von „der Farbladung“ als erhaltene Größe? Ich habe das bisher so verstanden, dass jeder Casimir-Op., der mit Hamiltonian kommutiert, exakt eine Erhaltungsgröße liefert, nicht? |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18062
|
 TomS Verfasst am: 02. Okt 2017 01:31 Titel: TomS Verfasst am: 02. Okt 2017 01:31 Titel: |
 |
|
Zum letzten Punkt: du hast nicht zwei sondern acht erhaltene Farbladungen!
Du kannst mal ein sehr einfaches Spielzeugmodell betrachten, nämlich den 3-dim. harmonischen Oszillator mit

mit den Farbladungen Q^a und den Generatoren T^a für a = 1..8
_{mn} a_n)
Es ist nette Algebra, zu beweisen, dass die Q's die selbe su(3) Algebra erfüllen wie die T's, dass alle Q's mit H vertauschen und somit erhalten sind, sowie dass aus den Q's auch die Casimir-Operatoren konstruiert werden können. |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 02. Okt 2017 11:30 Titel: index_razor Verfasst am: 02. Okt 2017 11:30 Titel: |
 |
|
| HansWerner hat Folgendes geschrieben: | | Ich habe das bisher so verstanden, dass jeder Casimir-Op., der mit Hamiltonian kommutiert, exakt eine Erhaltungsgröße liefert, nicht? |
Vielleicht noch ein Hinweis dazu: Mir scheint der Grund für deinen Irrtum darin zu liegen, daß du Invarianten und Erhaltungsgrößen durcheinanderbringst. Siehe z.B. deine Aussage zum Noether-Theorem:
| Zitat: |
Noether-Theorem stellt sicher, dass zur jeder Symmetrie eine Invariante existiert, [...]
|
Das Noether-Theorem besagt, daß zu jedem Generator einer Symmetriegruppe eine unabhängige Erhaltunsgröße gehört. Erhaltungsgrößen und Invarianten sind nicht dasselbe.
Erhaltungsgrößen 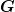 sind einfach Operatoren auf dem Hilbertraum (sie müssen nicht unbedingt irgendwas mit Lie-Algebren zu tun haben) und zeichnen sich dadurch aus, daß sie mit dem Hamiltonoperator vertauschen, also sind einfach Operatoren auf dem Hilbertraum (sie müssen nicht unbedingt irgendwas mit Lie-Algebren zu tun haben) und zeichnen sich dadurch aus, daß sie mit dem Hamiltonoperator vertauschen, also

gilt. Dies ergibt sich einfach daraus, daß der Operator  genau die Observable "zeitliche Änderung von G" definiert. genau die Observable "zeitliche Änderung von G" definiert.
Invarianten (wahrscheinlich muß man "differentielle Invarianten" sagen, wenn man nur infinitesimale Transformationen betrachtet)  kann man dadurch definieren, daß sie von allen Generatoren der Symmetriegruppe "vernichtet" werden, also durch kann man dadurch definieren, daß sie von allen Generatoren der Symmetriegruppe "vernichtet" werden, also durch

Was "vernichten" genau bedeutet, hängt davon ab um welche Objekte es sich bei Z handelt, und wie G auf sie wirkt. In der Darstellung der Algebra auf dem Hilbertraum ist diese Wirkung einfach durch

gegeben. In diesem Sinne ist das Noether-Theorem also eine Konsequenz daraus, daß H eine differentielle Invariante der durch die Generatoren G erzeugten Gruppe ist.
Mit Casimir-Operatoren hat das alles noch nicht direkt etwas zu tun. Casimir-Operatoren sind aber sowohl Invarianten der Algebra (immer) als auch Erhaltungsgrößen (nur, sofern es sich um eine Symmetrie-Gruppe handelt, also H ebenfalls invariant ist). Sie stammen aber im allgemeinen nicht aus der Lie-Algebra selbst (ein Beispiel dafür, daß nicht alle Erhaltungsgrößen Generatoren einer Symmetriegruppe sind), sondern aus der sogenannten universellen, einhüllenden Algebra der Lie-Algebra. Diese einhüllende Algebra enthält neben der Lie-Algebra selbst noch beliebige Polynome ihrer Generatoren. (Produkte und Polynome sind in Lie-Algebren normalerweise nicht definiert.) Die Casimir-Operatoren vertauschen mit allen Generatoren. Das macht sie zu Invarianten und auf Grund dieser Invarianz sind sie nützlich zur Klassifikation der irreduziblen Darstellungen der Lie-Algebra. Außerdem sind sie Polynome von Generatoren. Das macht sie zu Erhaltungsgrößen, nach den üblichen Regeln für Kommutatoren

etc. Sie sind aber m.E. nicht immer besonders wichtige Erhaltungsgrößen, (siehe z.B. das Quadrat der invariante Masse  , welches Casimir-Operator der Lorentz-Gruppe ist.) Ihre Bedeutung kommt hauptsächlich ihrer Invarianz zu. , welches Casimir-Operator der Lorentz-Gruppe ist.) Ihre Bedeutung kommt hauptsächlich ihrer Invarianz zu. |
|
 |
HansWerner
Anmeldungsdatum: 01.10.2017
Beiträge: 8
|
 HansWerner Verfasst am: 03. Okt 2017 17:02 Titel: HansWerner Verfasst am: 03. Okt 2017 17:02 Titel: |
 |
|
Allmählig kommt Licht ins Dunkle. Also die Generatoren sind stets Erhaltungsgrößen, allerdings nicht umgekehrt. Die einhüllende Algebra (bestünde aus Polynomen der Generatoren) umfasse jedoch alle Erhaltungsgrößen der korresp. Symmetriegruppe (=Liegruppe). Also für SU(2) wäre z.B. I^2 so eine Erhaltungsgröße, die nur in der einhüllenden, jedoch nicht der Lie-Algebra selbst liegt.
Die Quantenzahlen werden dann aus gleichzeitig diagonalisierbaren Elementen der einhüllenden A gewonnen? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Okt 2017 17:54 Titel: index_razor Verfasst am: 03. Okt 2017 17:54 Titel: |
 |
|
| HansWerner hat Folgendes geschrieben: | Allmählig kommt Licht ins Dunkle. Also die Generatoren sind stets Erhaltungsgrößen, allerdings nicht umgekehrt.
|
Ja, die Generatoren von Symmetriegruppen, also solchen mit Invariante H.
| Zitat: |
Die einhüllende Algebra (bestünde aus Polynomen der Generatoren) umfasse jedoch alle Erhaltungsgrößen der korresp. Symmetriegruppe (=Liegruppe).
|
Nicht notwendigerweise "alle". Z.B. ist mit  auch auch 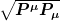 erhalten. Liegt aber, da es ja kein Polynom ist, nicht in der Algebra. Aber umgekehrt sind alle Elemente der Algebra auch Erhaltungsgrößen. erhalten. Liegt aber, da es ja kein Polynom ist, nicht in der Algebra. Aber umgekehrt sind alle Elemente der Algebra auch Erhaltungsgrößen.
| Zitat: |
Also für SU(2) wäre z.B. I^2 so eine Erhaltungsgröße, die nur in der einhüllenden, jedoch nicht der Lie-Algebra selbst liegt.
|
Ja, das stimmt.
| Zitat: |
Die Quantenzahlen werden dann aus gleichzeitig diagonalisierbaren Elementen der einhüllenden A gewonnen? |
Nur aus den Casimir-Operatoren und einer maximalen Menge gleichzeitig diagonalisierbarer Generatoren (letztere bilden die sog. Cartan-Unteralgebra). Mehr benötigt man im allgemeinen nicht. Die Eigenwerte der Casimir-Operatoren charakterisieren die endlich-dimensionalen irreduziblen Darstellungen und die Eigenwerte der Elemente der Cartanalgebra bestimmen dann die Zustände innerhalb dieser Darstellung. |
|
 |
HansWerner
Anmeldungsdatum: 01.10.2017
Beiträge: 8
|
 HansWerner Verfasst am: 03. Okt 2017 18:19 Titel: HansWerner Verfasst am: 03. Okt 2017 18:19 Titel: |
 |
|
|
Also man bildet kein Quantenzahlsystem zu ALLEN simultan diagonalisierbaren Elementen der einhüllenden Algebra, weil dies schlicht keine "neue Informationen" über das System liefert? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 03. Okt 2017 18:29 Titel: index_razor Verfasst am: 03. Okt 2017 18:29 Titel: |
 |
|
Ja, ich denke so kann man das sagen. Mit  sind ja auch sind ja auch  etc. diagonalisierbar. Liefern aber nichts neues. etc. diagonalisierbar. Liefern aber nichts neues. |
|
 |
HansWerner
Anmeldungsdatum: 01.10.2017
Beiträge: 8
|
 HansWerner Verfasst am: 03. Okt 2017 19:05 Titel: HansWerner Verfasst am: 03. Okt 2017 19:05 Titel: |
 |
|
Prima, wird mir verständlicher.
Noch eine generelle Frage zu Kopplung von Isospin-, Flavor-, Farbzuständen und ko:
Ist die Wirkung der diagonalisierbaren Generatoren bzw. Polynome der Generatoren als Operatoren auf die gekoppelten Zustände übertragbar auf die Art und Weise, wie ich es in meinem 2. Post am Beispiel von I^2 vorgeführt habe?
Also mit Standardtrick: gekoppelte Zustände in anderer Basis mittels CG-Koeffienzen ausdrücken und den Operator linear auf nun nicht mehr gekoppelte Basiselemente loslassen?
Hier nochmal das Schema (für I^2):

mit geeigneten CG-Koeffizieten a, b, c,d.
Und dann die Wirkung auf bel. Linearkombination

im Raum der gekoppelten Zustände nach obigem Muster ausdehnen?
Oder muss man da noch eine Subtilität beachten? |
|
 |
index_razor
Anmeldungsdatum: 14.08.2014
Beiträge: 3259
|
 index_razor Verfasst am: 04. Okt 2017 19:55 Titel: index_razor Verfasst am: 04. Okt 2017 19:55 Titel: |
 |
|
| HansWerner hat Folgendes geschrieben: |
Ist die Wirkung der diagonalisierbaren Generatoren bzw. Polynome der Generatoren als Operatoren auf die gekoppelten Zustände übertragbar auf die Art und Weise, wie ich es in meinem 2. Post am Beispiel von I^2 vorgeführt habe?
Also mit Standardtrick: gekoppelte Zustände in anderer Basis mittels CG-Koeffienzen ausdrücken und den Operator linear auf nun nicht mehr gekoppelte Basiselemente loslassen?
Hier nochmal das Schema (für I^2):

mit geeigneten CG-Koeffizieten a, b, c,d.
|
Wenn 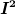 das Quadrat des Gesamtisospins sein soll, dann stimmt die Idee schon. Allerdings ist der Eigenwert ja h²I(I+1) also fehlt auf der rechten Seite wohl ein Faktor 2h. das Quadrat des Gesamtisospins sein soll, dann stimmt die Idee schon. Allerdings ist der Eigenwert ja h²I(I+1) also fehlt auf der rechten Seite wohl ein Faktor 2h. |
|
 |
|
|















