| Autor |
Nachricht |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 15. Jun 2017 12:39 Titel: Interferenz, Intensitäten und Zeigerdiagramm manuel459 Verfasst am: 15. Jun 2017 12:39 Titel: Interferenz, Intensitäten und Zeigerdiagramm |
 |
|
Hallo liebe Community
ich grüble jetzt schon lange über der Berechnung von der Gesamtintensität zweier sich überlagernder Wellen.
Dabei bin ich auf das Zeigerdiagramm gestoßen, das mir noch aus der Schule bekannt íst.
Nun frage ich mich, wenn ich zwei Wellen gegeben habe:
E1=E01*cos(wt-kx+phi1)
E2=E02*cos(wt-kx+phi2)
wie ich diese addieren soll.
Mir ist klar, dass man mithilfe des Zeigerdiagramms und des Cosinussatzes diese Addition leicht durchführen kann.
Was mir aber nicht klar ist, warum ich überhaupt das Zeigerdiagramm verwenden darf.
Ich versuche mal meine Erklärung zu zeigen:
ich kann nach additionstheoremen A*cos(x+phi) schreiben als a*cos(x)+b*sin(x) mit a=A*cos(phi) und b=A*sin(phi).
Da Cosinus und Sinus (mit welchem Skalarprodukt auch immer) linear unabhängig sind, bilden sie eine Basis (von was auch immer) und es gibt einen Isomorphismus zum R2 wodurch ich das dann so zeichnen darf.
Warum aber addiere ich das dann Vektoriell, sin(x) und cos(x) sind doch nur reelle Zahlen?
außerdem: Es wird dann immer eine Analogie zu e^(ix) geschlossen, da das ja cos(x)+i*sin(x) ist. Wie bekomme ich in meinem Additionstheorem dieses i hinein?
Hoffe mir kann jemand die Augen öffnen.
Danke und LG! |
|
 |
yellowfur
Moderator

Anmeldungsdatum: 30.11.2008
Beiträge: 804
|
 yellowfur Verfasst am: 15. Jun 2017 14:08 Titel: yellowfur Verfasst am: 15. Jun 2017 14:08 Titel: |
 |
|
Hallo Manuel!
Du hast da ziemlich viele Fragen und ich versuche, alles der Reihe nach abzuarbeiten:
| Zitat: | Nun frage ich mich, wenn ich zwei Wellen gegeben habe:
E1=E01*cos(wt-kx+phi1)
E2=E02*cos(wt-kx+phi2)
wie ich diese addieren soll. |
In diesem Fall kannst du sie nicht vereinfachen, da du unterschiedliche Amplituden E01 und E02 hast und gleichzeitig auch noch unterschiedliche (und nicht näher bestimmte) Phasen phi1 und phi2.
| Zitat: | | Mir ist klar, dass man mithilfe des Zeigerdiagramms und des Cosinussatzes diese Addition leicht durchführen kann. |
Ich denke, du meinst, wenn die Amplituden gleich sind, kann man den Term umschreiben als
+\cos(\phi_2 -kx + \omega t)) = 2A\cos(\frac{\phi_1}{2}-\frac{\phi_2}{2})\cos(\frac{\phi_1}{2}+\frac{\phi_2}{2}-kx+\omega t).)
Sowas in der Richtung? Man kann die Terme nur (sinnvoll) umschreiben, wenn entweder die Amplituden gleich sind (E01 = E02 = A) oder wenn die Phasen gleich sind (phi1 = phi2).
(In deinem Beispiel laufen die beiden Wellen bereits beide in x-Richtung und haben den gleichen k-vector und die gleiche Frequenz omega, das ist im Allgemeinen aber auch nicht der Fall. Wir betrachten also den Spezialfall, den du genannt hast.)
| Zitat: | Was mir aber nicht klar ist, warum ich überhaupt das Zeigerdiagramm verwenden darf.
Ich versuche mal meine Erklärung zu zeigen:
ich kann nach additionstheoremen A*cos(x+phi) schreiben als a*cos(x)+b*sin(x) mit a=A*cos(phi) und b=A*sin(phi). |
Du meinst =A\cos (x)\cos (\phi)-A\sin(x)\sin(\phi)) (mit Minuszeichen). (mit Minuszeichen).
Ja, es gibt eine ganze Reihe von Additionstheoremen. Aber warum gelten die?
Man muss sich anschauen, wie eine komplexe Zahl mit Zeigern darstellbar ist:
Du hast einen Realteil a und einen Imaginärteil b sodass 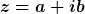 ist. ist.
Du hast quasi zwei Dimensionen, den Realteil und den Imaginärteil und die könnte man ja in einem zweidimensionalen Koordinatensyzstem darstellen.
In dem Dreieck würde die eine Linie auf der x-Achse liegen, die andere würde parallel zur y-Achse laufen und eine Art höhe beschreiben. Die Seitenverhältnisse im Dreieck sind genau mit sinus und cosinus des winkels beschreibbar.
Gleichzeitig kann man das aber auch mit dem Winkel in Polarkoordinaten beschreiben, also hast du  + \cos (\phi).
<br />
<br />
)
Das ist die Eulerformel:
https://de.wikipedia.org/wiki/Eulersche_Formel
Das war die anschauliche Erklärung, man kann das aber auch noch beweisen mithilfe der Reihendarstellung von sinus und kosinus.
Das bedeutet also, wenn ich den Realteil(den Cosinus) will, muss ich den Imaginärteil von cos(x)+isin(x) loswerden, wenn ich den Imaginärteil will, muss ich den Realteil loswerden.
So kann man auf die Idee kommen, dass
=\frac{exp(ix)+exp(-ix)}{2}) und und
=\frac{exp(ix)-exp(-ix)}{2i}.)
| Zitat: | | Da Cosinus und Sinus (mit welchem Skalarprodukt auch immer) linear unabhängig sind, bilden sie eine Basis (von was auch immer) und es gibt einen Isomorphismus zum R2 wodurch ich das dann so zeichnen darf. |
Ja so könnte man es komplizierter ausdrücken. Du brauchst halt Funktionen, die linear unabhängig sind (wenn du in x-Richtung läufst, willst du nur in x-Richtung laufen und nicht aus Versehen noch ein wenig in y-Richtung laufen, also sind (1,0) und (0,1) zB gut geeignete Basisvektoren) und das klappt immer dann gut, wenn das Funktionenskalarprodukt erfüllt ist, also \cos(x)dx=0.)
Also du weißt jetzt, wie man sinus und cosinus mit e-Funktionen darstellen kann und wenn man die einsetzt, kommen die Additionstheoreme mit den normalen Rechenregeln für Exponentialfunktionen usw ganz natürlich heraus.
Die Intensität, die du ganz oben nennst, ist 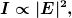
aber genau genommen, wenn du ein kompliziertes elektromagnetisches Nahfeld hast (wo noch keine zeitliche Mittelung usw durchgeführt wurde, ist sie der zeitliche Mittelwert des Poynting-Vektors. Also das würde jetzt noch ein ganz anderes Thema anschneiden:
https://de.wikipedia.org/wiki/Intensit%C3%A4t_(Physik)
Meistens kann man aber einfach zunächst das Betragsquadrat des E-Feldes betrachten.
Ich hoffe, das hilft 
_________________
Wenn du einen Traum hast, dann folge ihm. Wer weiß, wo er dich hinführen könnte. |
|
 |
manuel459
Anmeldungsdatum: 11.10.2016
Beiträge: 263
|
 manuel459 Verfasst am: 15. Jun 2017 22:52 Titel: manuel459 Verfasst am: 15. Jun 2017 22:52 Titel: |
 |
|
Hey!
Vielen Dank für die sehr ausführliche Antwort!
Viele Zusammenhänge sind mir jetzt klarer!
nun angenommen ich habe die zwei Wellen so gegeben:
E1=E01*cos(wt-kx+phi1)
E2=E02*cos(wt-kx+phi2)
und möchte deren Gesamtintensität ausrechnen.
Mit I proportional zu E^2.
Ich finde im Internet lediglich Herleitungen der Art wo Wellen durch e^(i*(kx-wt-phi) angeschrieben werden und diese direkt in |E1+E2|^2 eingesetzt werden & durchgerechnet. diese Form in meinem Fall zu benutzen wäre meiner Meinung nach nicht gut, da man ja wie du sagtest mit e^x*e^(-x) /2 rechnen müsste und das ein riesen Aufwand wäre.
Den zweiten Ansatz, den ich nun eben verfolge ist jener des Zeigerdiagramms.
Wenn ich einen Ausdruck A*cos(x+phi) gegeben habe, wie "beweise" ich dass ich das als um phi von der x-Achse aus gedrehten Vektor mit Länge A zeichnen darf?
Am ursprünglichen Beispiel:
da k-Vektor und w gleich sind, gilt dieser Teil ja als unwichtig wenn es um die Berechnung der Gesamtintensität geht.
Ich zeichne schlichtweg zwei Vektoren um jeweils phi1 bzw phi2 gegen den Uhrzeigersinn gedreht mit den Beträgen A1 und A2 und nach dem Cosinussatz ist dann
A3^2=A1^2+A2^2+2*A1*A2*cos(phi1-phi2) (mit Plus folgt aus Geometrischer Betrachtung und cos(pi-deltaphi)=-cos(deltaphi))
also wäre dieses Vorgehen einfacher.
Es scheitert bei mir jetzt nur noch an der "Umrechung" von dem cos in die Zeigerdarstellung.
LG
[/quote] |
|
 |
yellowfur
Moderator

Anmeldungsdatum: 30.11.2008
Beiträge: 804
|
 yellowfur Verfasst am: 19. Jun 2017 20:54 Titel: yellowfur Verfasst am: 19. Jun 2017 20:54 Titel: |
 |
|
Hallo Manuel,
Tut mir Leid, dass ich so spät antworte, ich musste mir erst einmal noch ein wenig Gedanken über deine Fragen machen.
Also erst einmal ist es ein Unterschied, ob du irgendeinen Term mit Cosinus benutzt oder einen Term mit einer e-Funktion oder ob du den einen Cosinus als e-Funktionen schreibst.
Es gibt dazu zwei Konzepte: Entweder du rechnest mit e-Funktionen, weil das einfacher ist, und sagst, alles, was am Schluss rauskommt, muss der Realteil des Ergebnisses sein. Das geht nur, wenn alle Gleichungen, die dazwischen vorkommen, linear sind. Quadratische Sachen sind nicht linear, also müsstest du, wenn du nur dafür die komplexe Schreibweise benutzt, |^2) schreiben. schreiben.
Oft will man aber die komplexe Schreibweise einführen, um das System gleichzeitig für sin und cos zu lösen (denn dann man hat wie im ersten Beitrag von mir beschrieben ja einen komplexen Zeiger), dann stimmt
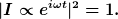
Weil du jetzt für cos und einen phasenverschobenen sin gleichzeitig löst, bekommst du ja immer nur die Amplitude heraus, du mittelst also die Zeit weg.
Was das bedeutet, ist Folgendes: Im zweiten Fall bekommst du die maximale Amplitude heraus, egal, an welchem Zeitpunkt die liegt.
Im ersten Fall bekommst du eine zeitabhängige Intensität, weil du die Zeit nicht wegmittelst. Wenn du also die maximale Intensität suchst, musst du noch schauen, bei welchem t deine Zeit maximal wird.
Der Unterschied kommt daher, dass du einmal eigentlich zwei Wellen hereinschickst, einen sinus und einen cosinus, und einmal hast du nur einen cosinus.
Die "richtige" (auch einheitenmäßige) Intensität ist eben der Poynting-Vektor, da verschwindet dann auch die Zeit immer und das gilt sowohl im Nahfeld als auch im Fernfeld. Mit dem Betragsquadrat schaut man sich "näherungsweise" die Intensität für ein Fernfeld an.
In deinem Fall weißt du die Welle genau, es ist ein Cosinus und du bekommst
+E_{02}*\cos(\omega t-kx+\phi_2)|^2= ) +E_{02}^2*\cos^2(\omega t-kx+\phi_2)+) *\cos(\omega t-kx+\phi_2).)
Das kann man nur noch wenig umschreiben und was bringt dir das dann? Die normalen Textbuchaufgaben sehen noch ein wenig anders aus, da kann man dann vereinfachen und sinnvoll ein Additionstheorem anwenden.
Wie gesagt, wenn du jetzt mit komplexen Zeigern rechnest, rechnest du etwas anderes, weil dann noch ein phasenverschobener Sinus dabei ist und die Rechnung nichtlinear ist. Es kommt ein bisschen darauf an, was du beschreiben willst.
_________________
Wenn du einen Traum hast, dann folge ihm. Wer weiß, wo er dich hinführen könnte. |
|
 |
|
|
















