| Autor |
Nachricht |
Interferatoraisor
Gast
|
 Interferatoraisor Verfasst am: 26. Apr 2006 17:53 Titel: Interferenz bei schrägem Lichteinfall auf Gitter Interferatoraisor Verfasst am: 26. Apr 2006 17:53 Titel: Interferenz bei schrägem Lichteinfall auf Gitter |
 |
|
Fällt kohärentes Licht senkrecht auf ein Transmissionsgitter ist der Gangunterschied ds ja recht einfach zu identifizieren.
 http://131.246.237.56/bilder/doppelspaltw.gif http://131.246.237.56/bilder/doppelspaltw.gif
Weil alle Punkterreger gleichzeitig angeregt werden(da senkrechter Lichteinfall) haben sie alle die gleiche Phase und für den Gangunterschied gilt bei maximaler Verstaerkung ds=k * wellenlaenge. Für Maxima gilt dann : g*sin(alpha) = k*lambda,
wobei g=gitterkonstante,k=Ordnund des Maximums, alpha=winkel unter dem das maximum k-ter Ordnung zu sehen ist lambda=Wellenlaenge
Meine Frage: Wie sieht es denn aus, wenn das Licht schräg auf das Gitter gerichtet ist, also nicht alle Erreger in Phase sind?
Bitte postet hier nicht nur eine Formel, sondern die Herleitung interessiert mich.
Vielen Dank im Voraus!
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 26. Apr 2006 19:15 Titel: as_string Verfasst am: 26. Apr 2006 19:15 Titel: |
 |
|
Hallo!
Dann hast Du einen Phasenunterschied bei den Elementarwellen. Die haben aber trotzdem noch die selbe Frequenz und die Phasendifferenz ist auch immer fest, so dass es trotzdem zu Interferrenz kommt.
Das aus zu rechnen ist eigentlich ziemlich leicht. Du machst Das nämlich genau so, wie auf der rechten Seite in Deiner Zeichnung auch. Du rechnest also zuerst die Wegdifferenz zu den zwei Schlitzen auf der rechten Seite aus und dann addierst Du die auf der linken Seite dazu.
Kommst Du mit dieser knappen Erklärung schon zurecht? Wenn nicht, dann poste nochmal, dann mache ich eine Zeichnung und leite es etwas weiter her. Aber wenn Du Dir erstmal selbst eine machst, dann hilft Dir das wahrscheinlich auch schon.
Gruß
Marco
|
|
 |
Interferatoraisor
Gast
|
 Interferatoraisor Verfasst am: 28. Apr 2006 07:18 Titel: Interferatoraisor Verfasst am: 28. Apr 2006 07:18 Titel: |
 |
|
So, ich hab jetzt ne Zeichnung angefertig und versucht da nen Gangunterschied zu identifizieren. Ich habe ja zwei unterschiedliche Winkel. Einmal den Einfallswinkel alpha_ein und den Ausfallswinkel alpha_aus. Bei benachbarten Erregern entstehen dann durch diese Winkel zwei Gangunterschiede ds0 und ds1. Insgesamt gilt dann: ds=ds0+ds1
Also ds=g * (cos(alpha_ein)+sin(alpha_aus)).
Ich hoffe, ich hab jetzt nicht alles falsch gemacht. Zur Not kannst du ja meine Skizze nehmen und entsprechend bearbeiten, so dass es richtig wird.
Danke!
| Beschreibung: |
|

Download |
| Dateiname: |
gangunterschied.png |
| Dateigröße: |
20.24 KB |
| Heruntergeladen: |
6479 mal |
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 28. Apr 2006 12:23 Titel: dermarkus Verfasst am: 28. Apr 2006 12:23 Titel: |
 |
|
Einverstanden!
Das einzige, was an deiner Herleitung ein bisschen ungewöhnlich aussieht, ist dass du den Einfallswinkel der Strahlen relativ zur Gitterebene definiert hast, während der Ausfallswinkel ja der Winkel zwischen Lichtstrahlen und der Gitternormalen ist.
Wenn du also auch deinen Einfallswinkel alpha_ein so definieren magst, dass er der Winkel zwischen einfallenden Lichtstrahlen und der Senkrechten auf der Gitterebene ist, dann steht da zweimal ein Sinus und die Formel sieht noch ein bisschen eingängiger aus.
---------------------------
Kannst du aus deiner Formel folgern, was bei schrägem Einfall passiert? Verschieben sich die Orte der Maxima auf dem Schirm? Ändert sich ihr Abstand zueinander?
|
|
 |
Interferatoraisor
Gast
|
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 28. Apr 2006 15:31 Titel: as_string Verfasst am: 28. Apr 2006 15:31 Titel: |
 |
|
| Interferatoraisor hat Folgendes geschrieben: | Mal angenommen ich untersuche das Hauptmaximum, dann gilt
 + \sin(\alpha_{aus})))
Diese Gleichung hat die Loesung: 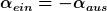 Ich interpretiere das einfach mal so, dass fuer das HauptMaximum gilt: einfallswinkel=ausfallswinkel(damit ist natuerlich keine reflektion gemeint). Ich interpretiere das einfach mal so, dass fuer das HauptMaximum gilt: einfallswinkel=ausfallswinkel(damit ist natuerlich keine reflektion gemeint). |
Ja, das ist richtig. Der Strahl geht also einfach gerade durch
| Interferatoraisor hat Folgendes geschrieben: | | Beim ersten Nebenmaximum muesste ich ja eigentlich zwei Loesungen fuer alpha_aus bekommen. Ich kriege da aber nichts vernuenftiges fuer raus. |
Normalerweise wirst Du den Winkel 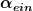 ja gegeben haben. Dann kannst Du Deine Gleichung umformen (nach sin(alpha_aus)) auflösen: ja gegeben haben. Dann kannst Du Deine Gleichung umformen (nach sin(alpha_aus)) auflösen:
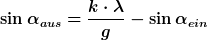
Durch den Einfallwinkel wird also der Sinus des Ausfallwinkels verkleinert. Das bewirkt also eine Verschiebung des gesamten Spektrums. Allerdings ist die nur bei kleinen Winkeln linear, ansonsten wird alles auch noch etwas gestaucht durch den Sinus, der da drin ist. Deshalb hat man das beste Ergebnis, wenn man irgendwelche Spektren ausmessen will normalerweise genau dann, wenn der Einfallwinkel 0° ist.
Gruß
Marco
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 28. Apr 2006 15:56 Titel: dermarkus Verfasst am: 28. Apr 2006 15:56 Titel: |
 |
|
| Interferatoraisor hat Folgendes geschrieben: | Stimmt meine Formel denn ueberhaupt? Und warum bekomme ich keine zwei Winkel als Loesung wenn ich das erste Nebenmaximum berechnen will?
|
Ja, deine Formel stimmt  Wenn du in dieser Formel die Werte k=1 und k=-1 einsetzt, dann bekommst du die beiden Winkel für das erste Nebenmaximum. Wenn du in dieser Formel die Werte k=1 und k=-1 einsetzt, dann bekommst du die beiden Winkel für das erste Nebenmaximum.
Und dein Ergebnis zeigt, dass sich bei schrägem Einfall die Lage der Maxima verschiebt. Der Abstand der Maxima voneinander auf dem Schirm (der ja parallel zur Gitterebene steht) dagegen bleibt in guter Näherung konstant, solange der Abstand des Schirms vom Gitter viel größer ist als die Entfernung der Maxima auf dem Schirm von der Schirmmitte.
Zuletzt bearbeitet von dermarkus am 28. Apr 2006 16:01, insgesamt einmal bearbeitet |
|
 |
as_string
Moderator

Anmeldungsdatum: 09.12.2005
Beiträge: 5791
Wohnort: Heidelberg
|
 as_string Verfasst am: 28. Apr 2006 15:58 Titel: as_string Verfasst am: 28. Apr 2006 15:58 Titel: |
 |
|
Hallo nochmal!
Ich habe das mal versucht durch zwei Plots etwas an zu deuten. Wenn Du Dir die Schnittpunkte zwischen den waagerechten Geraden und der Sinuskurve anschaust und dazu den x-Wert raussuchst, hast Du die Winkel, unter denen die verschiedenen Maxima auf den Schirm projeziert werden.
Auf dem ersten Graph ist der normale symmetrische Fall. Auf dem zweiten habe ich eine kleine Verschiebung der Waagerechten eingebaut, die aus dem Sinus des Einfallwinkels stammt. Wenn Du auch hier die dazugehörenden x-Werte Dir anschaust, dann siehst Du, dass die sich auch verschieben, aber nicht alle um den selben Betrag.
Hoffe, das machts vielleicht etwas deutlicher...
Gruß
Marco
PS:  Die Reihenfolge hat's leider rumgedreht. Also erst den unteren anschauen für symmetrisch, dann den oberen. Die Reihenfolge hat's leider rumgedreht. Also erst den unteren anschauen für symmetrisch, dann den oberen.
| Beschreibung: |
|
| Dateigröße: |
4.48 KB |
| Angeschaut: |
13669 mal |

|
| Beschreibung: |
|
| Dateigröße: |
4.26 KB |
| Angeschaut: |
13595 mal |

|
|
|
 |
Interferatoraisor
Gast
|
 Interferatoraisor Verfasst am: 28. Apr 2006 16:14 Titel: Interferatoraisor Verfasst am: 28. Apr 2006 16:14 Titel: |
 |
|
| Zitat: | | //[as_string] Edit: Ich habe etwas Dein Latex aufgeräumt. Ich hoffe das ist in Deinem Sinne |
Ja, super danke 
Ich moechte jetzt einmal die beiden Winkel des ersten Nebenmaximums fuer g=4*10^-5m und lambda=600*10^-9m und alpha_ein=45°
Wenn ich in die Formel einsetze und nach alpha_aus umforme bekomme ich folgendes Ergebnis: -43.797
Ok, dann schliesse ich jetzt mal daraus, dass das der Winkel ist, dessen zugehoeriges Maximum bzgl. der Gitternormalen "innen" liegt.
Wenn ich jetzt das "aeussere" Maximum haben will, darf ich einfach folgendes machen: 45+(45-43.797)=46.203° ?
|
|
 |
Interferatoraisor
Gast
|
 Interferatoraisor Verfasst am: 28. Apr 2006 16:20 Titel: Interferatoraisor Verfasst am: 28. Apr 2006 16:20 Titel: |
 |
|
Oh, da habt ihr schon in der Zwischenzeit geantwortet und ich habs nicht gelesen, bevor ich meinen Post abgeschickt hatte.
| Zitat: | | Wenn du in dieser Formel die Werte k=1 und k=-1 einsetzt, dann bekommst du die beiden Winkel für das erste Nebenmaximum. |
Super, dann weiss ich ja jetzt wies geht. Dann entfaellt die Frage meines letzten Posts.
Vielen Dank euch Marco&Markus, habt euch viel Muehe gemacht! 
|
|
 |
Roman
Gast
|
 Roman Verfasst am: 28. Apr 2006 17:17 Titel: Roman Verfasst am: 28. Apr 2006 17:17 Titel: |
 |
|
Hi hab den Thread gelesen und als sehr hilfreich empfunden! Danke! Nur habe ich eine Frage! Warum bekomment man negative Winkel vom Taschenrechner ausgespuckt? Und wie hab ich dieses Minus dann zu deuten? 
Gruß Roman
|
|
 |
dermarkus
Administrator

Anmeldungsdatum: 12.01.2006
Beiträge: 14788
|
 dermarkus Verfasst am: 28. Apr 2006 17:19 Titel: dermarkus Verfasst am: 28. Apr 2006 17:19 Titel: |
 |
|
|
Wenn positive Winkel hier eine Ablenkung nach links bedeuten, dann sind negative Winkel entsprechend Ablenkungen nach rechts.
|
|
 |
|


















 Wenn du in dieser Formel die Werte k=1 und k=-1 einsetzt, dann bekommst du die beiden Winkel für das erste Nebenmaximum.
Wenn du in dieser Formel die Werte k=1 und k=-1 einsetzt, dann bekommst du die beiden Winkel für das erste Nebenmaximum.
 Die Reihenfolge hat's leider rumgedreht. Also erst den unteren anschauen für symmetrisch, dann den oberen.
Die Reihenfolge hat's leider rumgedreht. Also erst den unteren anschauen für symmetrisch, dann den oberen.

