| Autor |
Nachricht |
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
 schnudl Verfasst am: 30. Aug 2016 08:38 Titel: Lorentzgruppe und Spinoren |
 |
|
Die Lorentzgruppe SO(3,1) wird doch durch 6 Generatoren gebildet, nämlich drei Drehungen J und drei Boosts K.
Dabei sind K und J 4x4 Matrizen, die den Vertauschungsrelationen
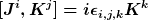
Bis daher kann ich das noch gut verstehen.
Im Ryder wird nun die Diracgleichung anhand von Überlegungen motiviert die ich ab einem bestimmten Punkt nicht mehr verstehen kann.
Es wird gesagt, dass man
)
und
)
definiert , die dann
und
und somit A und B jeweils der SU(2) Algebra genügen.
Die erste Frage ist gleich:
SU(2) ist nach meinem Wissen die Gruppe der unitären 2x2 Matrizen, mit det=1. Wieso sind dann 4x4 Matrizen plötzlich auch in SU(2)? Die Frage ist sicher dumm, für jemanden der sich da echt auskennt, aber ich sehe da nur Mattscheibe.
Weiter unten steht dann, dass sich die Zustände nach (j, j') klassiifzieren lassen, wobei J mit A und j' mit B korrespondiert.
(j, 0) entspricht dann B=0 und (0,j') entspricht A=0.
Wenn ich aber B=0 setze, habe ich
Wenn ich mir nun aber die 4x4 Matrizen für J (Drehungen) und K (Boosts) ansehe, so ist J aber eben nicht iK. Ich verstehe daher nicht was da abgeht...Oder sind mit J und K plötzlich andere, allgemeine 4x4 Matrizen gemeint, die die SU(2) Algebra erfüllen?
Es steht ja eigentlich genauer da
} = i K^{(j)})
wobei (j) den Drehimpuls angibt. Haben diese Matrizen nun unterschiedliche Größen, je nachdem welches j man nimmt?
Weiter unten steht dann sogar:
} = \sigma/2)
und das wären ja 2x2 Matrizen.
Wieso geht man erst von 4x4 Matrizen aus und landet dann auf einmal bei 2x2 Darstellungen? Was hat das eine mit dem anderen zu tun?
Hier steige ich konsequent aus und weiß nicht mehr, wovon eigentlich die Rede ist...
Ich würde das ganze gerne verstehen, finde aber nirgendwo gute Erklärungen, die ohne Grundlagenwissen auskommen. Wo wird das von der Pieke an erklärt? Es gibt viele Abhandlungen zum Nachlesen, aber irgendwie setzen die alle schon voraus, dass man über die Zusammenhänge zwischen SU(x), SO(3,1) und SL(2,C), .... schon Bescheid weiß...
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
 |
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
| bassiks Verfasst am: 30. Aug 2016 09:59 Titel: |
|
|
Schnelle Version:
Betrachte mal einen Vektor  .
Betrachte nun die Paulimatrizen ) .
Weiters gelte  .
Folgende Regel gilt ebenfalls:
(\vec{y}\cdot\vec{\sigma})=\vec{x}\cdot\vec{y}+i\vec{\sigma}\cdot(\vec{x}\times\vec{y})) . (Kann man nachrechnen  )
Betrachte nun den Operator: =e^{-\frac{i}{2}\vec{\alpha}\vec{\sigma}}) , welcher offensichtlich ein Element der SU(2) ist.
Weiters gilt:
\vec{x}\cdot\vec{\sigma}U^\dagger(\vec{\alpha})=[\cos\alpha\vec{x}+\sin\alpha\vec{n}\times\vec{x}+(1-\cos\alpha)\vec{n}\cdot\vec{x}\vec{n}]\cdot\vec{\sigma})
Der Ausdruck in der Klammer ist Euler's Formel für eine 3-dimensionale Rotation (siehe https://en.wikipedia.org/wiki/Axis%E2%80%93angle_representation). Die rechte Seite kann also geschrieben werden als eine Rotation des Vektors  um die Achse  und den Winkel  und anschließender Multiplikation mit  , also
\vec{x}\cdot\vec{\sigma}U^\dagger(\vec{\alpha}) = [R(\vec{\alpha})\vec{x}]\cdot\vec{\sigma}) .
Die Abbildung \to SU(2), R(\vec{\alpha})\mapsto U(\vec{\alpha})) ist also eine Darstellung der SO(3). (Nicht 1:1 sondern 1:2, aber das sind Details).
Geht man über in den Minkowski-Raum, und erweitert die Paulimatrizen um  , so führt eine analoge Überlegung dazu, dass man nun nicht nur die Drehungen, sondern auch Boosts erhält, und somit eine SU(2) Darstellung der eigentlichen Lorentzgruppe erhält. (Wieder nicht 1:1 sondern 1:2). Diese nennt man Spinor-Darstellung })
Ich hoffe ich hab mich nirgends vertippt und konnte etwas weiter helfen. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 30. Aug 2016 20:26 Titel: |
|
|
Ich würde gerne etwas grundsätzlicher anfangen.
Eine Gruppe ist vollständig definiert über die Verknüpfungstabelle zur Gruppenoperation, d.h. über die vollständige Auflistung aller Paare von Gruppenelementen sowie dem Ergebnis
Jede konkrete Realisierung, die diese Verknüpfung respektiert heißt Darstellung der Gruppe; im Falle der Liegruppen sind dies u.a. quadratische n*n Matrizen, die auf n-dim. Vektorräumen operieren. Eine Darstellung D ordnet einem abstrakten Gruppenelement g eine Matrix D(g) zu; es muss gelten
 \cdot D(g_2) = D(h))
Die Darstellungen j der SU(2) werden durch ihre Dimension n gekennzeichnet:
Es gilt
Die ganzzahligen Darstellungen entsprechen exakt den Darstellungen der SO(3). Die sogenannte Vektor-Darstellung j = 1 mit n = 3 entspricht den Rotationen von 3-dim. Vektoren. Die sogenannte Spinor-Darstellung j = 1/2 mit n = 2 entspricht den Rotationen von 2-dim. komplexen Vektoren.
Die bisher genannten Darstellungen lassen sich nicht weiter zerlegen; deswegen nennt man sie irreduzibel. Man kann trivialerweise auch reduzible Darstellungen konstruieren, indem man zwei (oder mehr) Darstellungen j_1 und j_2 in Form von blockdiagonalen Matrizen kombiniert, wobei jeder Block selbst der Darstellung j_1 bzw. j_2 entspricht.
Genau dieser Fall liegt bei den Dirac-Spinoren und der o.g. Zerlegung in die beiden 2-dim. su(2) Darstellungen A und B vor. Dass die so(3,1) in zwei Algebren
 \simeq su(2) \oplus su(2))
zerfällt, stellt eine Ausnahme dar. Daraus resultieren einige spezielle Eigenschaften der Darstellungen sowie Besonderheiten der 4-dim. Raumzeit, die für andere Dimensionen nicht gegeben ist. Die Existenz von Twistoren sowie die spezielle Konstruktion der Schleifenquantengravitation hängt mit diesen Eigenschaften zusammen. |
|
|
schnudl
Moderator
Anmeldungsdatum: 15.11.2005
Beiträge: 6979
Wohnort: Wien
|
| schnudl Verfasst am: 31. Aug 2016 12:10 Titel: |
|
|
Danke euch beiden, ich muss zugeben, dass ich das momentan (noch) nicht so ganz verstehen kann.
SU(2) ist die Gruppe der unitären 2x2 Matrizen A mit det(A)=1.
Und obwohl es sich hier um 2x2 Matrizen handelt, gibt es Darstellungen mit höherer Dimension.
Ich versuche mal einen gang ganz amateuerhaften Verständnisansatz (bitte nun nicht auslachen):
Da es ja drei Erzeugende gibt (das sind ja die 3 Pauli Matrizen) und diese die Dimension 2x2 haben lässt sich jedes "native" Element von SU(2) schreiben als
 = e^{i \vec \alpha \cdot \vec \sigma/2})
Bedeutet das dann, dass man als "abstraktes Gruppenelement" den Vektor  betrachtet?
Den Schritt zu höher dimensionalen Darstellungen habe ich noch nicht gerafft. Heißt es dann z.B. für j=1, ich ordne eine 3x3 Matrix ) zu?
Dann müsste für die abstrakten Gruppenelemente
folgen, dass
 M(\beta) = M(\gamma))
Um die Gruppeneigenschaften zu wahren? Und dafür müssen die Matrizen M besondere Eigenschaften haben, aber nicht notwendigerweise 2x2 dimensional?
Ich komme jedenfalls zum Schluss, dass man mit Literatur über Quantenfeldtheorie gar nicht mal anzufangen braucht, solange man nicht die Grundprinzipien der Theorie der Lie Gruppen usw. einigermaßen beherrscht. Ich frage mich nun, wo man das lernen kann, in einer mathematischen Tiefe, die für Physiker angemessen ist und nicht in unnötige mathematische Details abgleitet.
Ich habe mal Relativität, Gruppen Teilchen von Sexl/Urbantke angeschaut. reicht dieses Werk aus oder ist es gar zu umfangreich ?
_________________
Wenn du eine weise Antwort verlangst, musst du vernünftig fragen (Goethe) |
|
|
bassiks
Anmeldungsdatum: 11.08.2010
Beiträge: 194
|
| bassiks Verfasst am: 31. Aug 2016 14:34 Titel: |
|
|
| schnudl hat Folgendes geschrieben: | SU(2) ist die Gruppe der unitären 2x2 Matrizen A mit det(A)=1.
Und obwohl es sich hier um 2x2 Matrizen handelt, gibt es Darstellungen mit höherer Dimension. |
Eigentlich betrachtet man hier meist die Lorentzgruppe und sucht Darstellungen dieser in verschiedenen Dimensionen. Du musst unterscheiden zwischen der Gruppe selbst, und ihrer Darstellung. TomS hat das in seinem Beitrag auch geschrieben:
| TomS hat Folgendes geschrieben: | | Jede konkrete Realisierung, die diese Verknüpfung respektiert heißt Darstellung der Gruppe; |
Die Lorentzgruppe besitzt zum Beispiel eine Darstellung in Form von 4x4 Matrizen, welche auf Vierervektoren wirkt. Diese ist dir sicher geläufig. Will man nun untersuchen wie sich andere Objekte transformieren (zum Beispiel ein Dirac-Spinor), benötigt man eine entsprechende Darstellung der Lorentzgruppe.
| Schnudl hat Folgendes geschrieben: | | Ich habe mal Relativität, Gruppen Teilchen von Sexl/Urbantke angeschaut. reicht dieses Werk aus oder ist es gar zu umfangreich ? |
Ich kenne das Buch leider nicht. Evt. hilft es dir auch einfach mal nach "Spinordarstellung der Lorentzgruppe" zu googlen (erstes Ergebnis: http://pauli.uni-muenster.de/tp/fileadmin/lehre/teilchen/ss08/Lorentzgruppe.pdf, weiß aber nicht ob das gut ist, habs nicht gelesen). |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
| TomS Verfasst am: 31. Aug 2016 16:41 Titel: |
|
|
Deine Schlussfolgerungen sind im wesentlichen korrekt, mit Ausnahme der Idee, dass die drei Winkel den abstrakten Elementen entsprechen. Die abstrakten Elemente sind und bleiben nunmal abstrakt :-)
Die Winkel können verschieden gewählt werden, z.B. kann man die 3*3 Darstellung der SO(3) einerseits mittels Eulerwinkeln sowie andererseits in einer Form
konstruieren; es handelt sich in beiden Fällen um die selbe Darstellung, jedoch unterschiedliche Parameter.
Die definierende bzw. Fundamentaldarsellung der SU(2) ist tatsächlich die mittels der 2*2-Matrizen.
Die triviale Darstellung besteht nur aus der Zahl Eins. Beachte: sie erfüllt die von mir o.g. Bedingung an eine Darstellung. Sie ist jedoch nicht treu, d.h. dass die Darstellung verschiedene Elemente der Gruppe auf das selbe Element der Darstellung abbildet:
 = D(g_2))
Im selben Sinne sind auch alle höherdimensionalen Darstellungen der SO(3) ihrerseits Darstellungen der SU(2), speziell auch die 3*3 Matrizen der SO(3); diese sind bzgl. der SU(2) allesamt nicht treu.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
