| Autor |
Nachricht |
Jamuriquai
Anmeldungsdatum: 05.06.2016
Beiträge: 4
|
 Jamuriquai Verfasst am: 06. Jun 2016 00:29 Titel: Bahndrehimpuls eines Elektrons in würfelförmigem Potential Jamuriquai Verfasst am: 06. Jun 2016 00:29 Titel: Bahndrehimpuls eines Elektrons in würfelförmigem Potential |
 |
|
Meine Frage:
Hallo!
Ich beschäftige mich gerade mit einer Aufgabe, in der es darum geht, den Drehimpuls eines Elektrons zu berechnen, das in einem würfelförmigen Potentialtopf mit der Kantenlänge 2a gefangen ist. Außerhalb des Würfels ist das Potential unendlich, innerhalb des Würfels ist es 0.
Berechnet werden soll der Erwartungswert von  (den man auch so notieren könnte (den man auch so notieren könnte  ) im Grundzustand. ) im Grundzustand.
Meine Ideen:
Der Symmetrie des Problems entspricht es sicherlich eher, das Problem in kartesischen Koordinaten zu lösen. Leider konnte ich nur Hinweise zu kugelsymmetrischen Problemen dieser Art finden. Wenn ich es richtig verstehe, lautet das allgemeine Resultat für den Drehimpuls eines Elektrons in einem Zentralpotential:
 )
Demnach wäre der Drehimpuls im Grundzustand l = 0 ebenfalls 0. Ich könnte mir jedoch vorstellen, dass dieses Resultat für das Würfelpotential aufgrund der unterschiedlichen Symmetrie nicht gilt.
Ich denke, dass Leiteroperatoren für die Lösung nötig sind, insbesondere wahrscheinlich die folgende Beziehung:
 + (L_z)^2 )
Zum einen verstehe ich das Konzept der Leiteroperatoren nicht vollständig, zum anderen habe ich nur Beispiele für deren Verwendung in Kugelkoordinaten gefunden.
Wie kann ich Leiteroperatoren hier verwenden, um den Drehimpuls in kartesischen Koordinaten zu berechnen? Ist es, nachdem man mit den Leiteroperatoren einen  -Operator gefunden hat, nötig ein Integral von der folgenden Form zu lösen (mit der Wellenfunktion des Grundzustands -Operator gefunden hat, nötig ein Integral von der folgenden Form zu lösen (mit der Wellenfunktion des Grundzustands 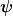 )? )?

Oder ist ein ganz anderer Ansatz nötig?
Vielen Dank im Voraus! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
 TomS Verfasst am: 06. Jun 2016 06:58 Titel: TomS Verfasst am: 06. Jun 2016 06:58 Titel: |
 |
|
Du kannst den Drehimpulsoperator wie üblich in sphärischen Koordinaten definieren, du musst sie Eigenzustände jedoch tatsächlich in kartesischen Koordinaten berechnen.
Das Potential und damit die Eigenzustände weisen keine sphärische Symmetrie auf, deswegen vertauscht der Drehimpuls L nicht mit dem Hamiltonoperator H. D.h. L ist nicht erhalten, oder - wie man auch sagt - keine gute Quantenzahl. Die Eigenzustände zu H sind keine Eigenzustände zu L.
Wenn du möchtest, kannst du dennoch den Erwartungswert <L> je Komponente oder für L^2 berechnen; das ist jedoch m.E. nicht besonders nützlich.
Wenn du möchtest, kannst du die notwendigen Operatoren in kartesische Koordinaten umformen; dazu musst du lediglich die Differentialoperatoren transformieren. Aber wie gesagt, das ist eine lange Rechnung ohne nützliches Ergebnis.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Jamuriquai
Anmeldungsdatum: 05.06.2016
Beiträge: 4
|
 Jamuriquai Verfasst am: 07. Jun 2016 01:54 Titel: Jamuriquai Verfasst am: 07. Jun 2016 01:54 Titel: |
 |
|
Vielen Dank für die schnelle Antwort TomS, deine Hinweise haben mir weitergeholfen!
Ich habe ein bisschen gerechnet, bin mir aber unsicher, ob ich alles richtig gemacht habe, daher wären Hinweise auf Fehler super:
Als tiefsten Eigenzustand/Wellenfunktion im Grundzustand habe ich die Folgende verwendet (ist die Normierung so richtig?):
 = \sqrt{1/a^3} * cos(\frac{\pi}{2a} x)* cos(\frac{\pi}{2a} y)* cos(\frac{\pi}{2a} z) )
Als Differentialoperatoren habe ich direkt die Drehimpulsoperatoren in kartesischen Koordinaten verwendet, ich habe zunächst die Rechnung nur in der x-Komponente durchgeführt. Ich dachte es ist einfacher, direkt die Drehimpulsoperatoren in kartesischen Koordinaten zu verwenden, anstatt erst mühsam eine Transformation der Operatoren in Kugelkoordinaten durchzuführen:
 )
Dann habe ich das folgende Integral berechnet und als Ergebnis 0 erhalten:

Ich vermute, dass das Ergebnis der anderen Integrale (auf die gleiche Art und Weise berechnet) für y- und z-Komponente des Drehimpulses ebenfalls 0 ist. Folgt daraus also, dass der Drehimpuls für dieses Systems im Grundzustand 0 ist?
Zwei Sachen sind mir noch unklar:
- Was folgt daraus, dass der Drehimpuls L nicht mit dem Hamiltonoperator H vertauschbar ist (also in dem Sinne: hat das Konsequenzen für die Aufgabe hier..)?
- Ich habe es so verstanden, dass sich nur eine Komponente des Drehimpulses und L^2 gleichzeitig scharf bestimmen lassen. Wenn ich aber, wie oben getan, Komponentenweise L bestimme (und für jede Komponente 0 erhalte), dann bestimme ich doch alle 3 Komponenten gleichzeitig, was aber eigentlich nicht möglich sein sollte? Müsste ich aus dem Grund einen anderen Lösungsweg einschlagen?
Ich wäre sehr dankbar für einige weitere Hinweise (und muss das Problem mit langer Rechnung und unnützem Ergebnis dankbarerweise als Übungsaufgabe bearbeiten  )! )! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
 TomS Verfasst am: 07. Jun 2016 10:49 Titel: TomS Verfasst am: 07. Jun 2016 10:49 Titel: |
 |
|
Im Sinne der Aufgabe genügt es, den Erwartungswert zu berechnen.
Ob ein Zustand jedoch einen bestimmten Drehimpuls hat folgt aus der Anwendung des Operators auf die Wellenfunktion, z.B.

Nur wenn dabei ein Eigenzustand vorliegt, wenn also

gilt, dann hat dieser Zustand der Drehimpuls lambda.
Dies ist bei deiner Wellenfunktion offensichtlich nicht der Fall.
Du berechnest jedoch Erwartungswerte, und da erhältst du natürlich je Komponente eine feste Zahl; die darfst du jedoch nicht mit dem Eigenwert des Drehimpulses verwechseln. |
|
 |
W.Atom
Gast
|
 W.Atom Verfasst am: 07. Jun 2016 11:28 Titel: W.Atom Verfasst am: 07. Jun 2016 11:28 Titel: |
 |
|
@Tom.S
Der Drehimpuls des Elektrons im Wasserstoffatom z.b. ist im Grundzustand (S-Zustand) ist gleich Null oder ?
Wie Soll (kann) man sich die Bewegung des Elektrons in diesem Zustand vorstellen?
|
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
 TomS Verfasst am: 07. Jun 2016 11:37 Titel: TomS Verfasst am: 07. Jun 2016 11:37 Titel: |
 |
|
| W.Atom hat Folgendes geschrieben: | | Der Drehimpuls des Elektrons im Wasserstoffatom z.b. ist im Grundzustand (S-Zustand) ist gleich Null |
Der Grundzustand ist n = 1; ein S-Zustand mit l = 0 existiert für jedes n = 1,2,3,...
| W.Atom hat Folgendes geschrieben: | | Wie Soll (kann) man sich die Bewegung des Elektrons in diesem Zustand vorstellen? |
Am besten gar nicht, denn es ist



Allerdings gilt
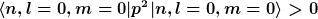
Man kann sich das nicht in Form einer klassischen Bewegung vorstellen, höchstens als stehende Welle. |
|
 |
Jamuriquai
Anmeldungsdatum: 05.06.2016
Beiträge: 4
|
 Jamuriquai Verfasst am: 07. Jun 2016 15:20 Titel: Jamuriquai Verfasst am: 07. Jun 2016 15:20 Titel: |
 |
|
Vielen Dank für deine Hilfe TomS, ich denke, ich habe jetzt alles verstanden!
Nur um sicherzugehen: Mit der obigen Vorgehensweise habe ich die Erwartungswerte des Drehimpulses aller Komponenten <Li> berechnet, die jeweils 0 sind, womit auch:

gilt.
Weil es sich dabei um Erwartungswerte einer Observablen handelt, sind alle 3 gleichzeitig berechenbar. Gäbe es scharf bestimmbare Erwartungswerte, die in diesem Zustand des Systems bei jeder Messung genau den gleichen Wert haben, müsste die obige Eigenwertgleichung gelten. Dies ist für dieses System aber in keiner Komponente der Fall.
Wenn ich jetzt in sphärischen Koordinaten mit einem Zentralpotential rechne z.B. mit l=1 und m=1 und die scharfbestimmbare Komponente in die z-Achse lege, dann würde nur für die z-Komponente des Drehimpulses die Eigenwertgleichung gelten, richtig? Außerdem wären die Erwartungswerte des Drehimpulses in der x- und y-Komponente 0, nehme ich an?
Rein aus Interesse: Woran liegt es, dass beim Wasserstoffatom im Grundzustand für den Erwartungswert des Impulsquadrates p^2 > 0 gilt? Ergibt sich das nur mathematisch oder kann man das auch anschaulicher verstehen?
Besten Dank nochmals! |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18051
|
 TomS Verfasst am: 07. Jun 2016 15:32 Titel: TomS Verfasst am: 07. Jun 2016 15:32 Titel: |
 |
|
| Jamuriquai hat Folgendes geschrieben: | Vielen Dank für deine Hilfe TomS, ich denke, ich habe jetzt alles verstanden!
Nur um sicherzugehen: Mit der obigen Vorgehensweise habe ich die Erwartungswerte des Drehimpulses aller Komponenten <Li> berechnet, die jeweils 0 sind, womit auch:

gilt. |
Das ist möglicherweise der Fall, aber das musst du separat zeigen, denn

| Jamuriquai hat Folgendes geschrieben: | | Dies ist für dieses System aber in keiner Komponente der Fall. |
Wie lautet denn das Ergebnis, wenn du die L_i auf die gegebene Wellenfunktion anwendest?
| Jamuriquai hat Folgendes geschrieben: | | Wenn ich jetzt in sphärischen Koordinaten mit einem Zentralpotential rechne z.B. mit l=1 und m=1 und die scharfbestimmbare Komponente in die z-Achse lege, dann würde nur für die z-Komponente des Drehimpulses die Eigenwertgleichung gelten, richtig? |
Ja.
(Mit der Ausnahme, wenn alle L_i Null liefern)
| Jamuriquai hat Folgendes geschrieben: | | Rein aus Interesse: Woran liegt es, dass beim Wasserstoffatom im Grundzustand für den Erwartungswert des Impulsquadrates p^2 > 0 gilt? Ergibt sich das nur mathematisch oder kann man das auch anschaulicher verstehen? |
Man kann das z.B. mit einer quantenmechanischen Form des Virialsatzes in Verbindung bringen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
Jamuriquai
Anmeldungsdatum: 05.06.2016
Beiträge: 4
|
 Jamuriquai Verfasst am: 12. Jun 2016 21:06 Titel: Jamuriquai Verfasst am: 12. Jun 2016 21:06 Titel: |
 |
|
Vielen Dank für die letzte Antwort TomS (Entschuldigung, dass ich mich erst jetzt melde..)!
Dein Hinweis war auf jeden Fall entscheidend, denn in diesem Fall ist der Erwartungswert von L^2 tatsächlich nicht 0, während der Erwartungswert von L gleich 0 ist. Vielen Dank! |
|
 |
|
|
















 )!
)!