| Autor |
Nachricht |
ph113
Anmeldungsdatum: 13.05.2016
Beiträge: 7
|
 ph113 Verfasst am: 13. Mai 2016 20:46 Titel: Definition gebundene Zustände/Streuzustände & Reflexion/ ph113 Verfasst am: 13. Mai 2016 20:46 Titel: Definition gebundene Zustände/Streuzustände & Reflexion/ |
 |
|
Meine Frage:
Hallo, ich habe einige Fragen zu den Definitionen von Streuzuständen und gebundenen Zuständen sowie zum Reflexions-/Transmissionskoeffizienten.
1) In der Vorlesung haben wir gebundene Zustände als die Zustände mit E<0 und Streuzustände als solche mit E>0 definiert.
Sind Streuzustände nie normierbar und haben immer ein kontinuierliches Energiespektrum bzw. sind gebundene Zustände immer normierbar mit diskretem Energiespektrum? Falls ja, woraus folgt das formal?
2) Hat man beispielsweise ein Delta-Potential bei 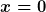 , so erhält man als Lösungen der Schrödinger-Gleichungen , so erhält man als Lösungen der Schrödinger-Gleichungen =Ae^{ikx}+Be^{-ikx}) für für 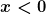 und analog und analog =Fe^{ikx}+Ge^{-ikx}) für für  . Wenn man Streuung von links betrachtet, setzt man . Wenn man Streuung von links betrachtet, setzt man  und definiert den Reflexionskoeffizienten und definiert den Reflexionskoeffizienten  sowie den Transmissionskoeffizienten sowie den Transmissionskoeffizienten 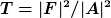 . .
Meine Fragen:
Wieso kann man einfach sagen, dass  sein muss, wenn man Streuung von links betrachtet? Ich meine wenn ein Teilchen durch ein Wellenpaket beschrieben werden kann, warum dann nicht durch die Summe zweier ebener Wellen? Warum kann keine zweite Welle nach links laufen? Mir fehlt hier wahrscheinlich der Zusammenhang. sein muss, wenn man Streuung von links betrachtet? Ich meine wenn ein Teilchen durch ein Wellenpaket beschrieben werden kann, warum dann nicht durch die Summe zweier ebener Wellen? Warum kann keine zweite Welle nach links laufen? Mir fehlt hier wahrscheinlich der Zusammenhang.
Der Relfexions- und der Transmissionskoeffizient geben ja die Wahrscheinlichkeit dafür an, dass ein Teilchen reflektiert bzw. transmittiert wird, richtig? Warum ist dies gerade durch den Quotienten des Betragsquadrats gegeben? Auch hier interessiert mich eine mathematische Begründung.
3) Oft hat man in der Wellenfunktion Ausdrücke wie z.B. =Ae^{kx}+Be^{-kx}) für für  . Muss man nun immer den ersten Term . Muss man nun immer den ersten Term  ausschließen, weil dieser für große ausschließen, weil dieser für große  divergiert, oder macht man das nur bei den gebundenen Zuständen, da die Streuzustände eh nicht normierbar sind? divergiert, oder macht man das nur bei den gebundenen Zuständen, da die Streuzustände eh nicht normierbar sind?
4) Muss die Energie E immer größer sein, als das Minimum des Potentials, oder nur bei gebundenen Zuständen?
Für jede Antwort bin ich dankbar.
LG
Meine Ideen:
Ich habe mir auch schon diese Themen im Griffiths durchgelesen, leider sind meine Fragen dadurch nicht geklärt.
Zuletzt bearbeitet von ph113 am 13. Mai 2016 21:51, insgesamt einmal bearbeitet |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 13. Mai 2016 21:25 Titel: Jayk Verfasst am: 13. Mai 2016 21:25 Titel: |
 |
|
Zu 1) Ganz sicher ist das nicht immer so. Denn es hindert Dich ja niemand daran, zum Hamiltonoperator einfach eine Konstante zu addieren. Das ändert das physikalische System nicht. Mir ist auch nicht bekannt, daß man allgemein Schlußfolgerungen ziehen kann, wie der kontinuierliche und der diskrete Teil des Spektrums verteilt sind.
Zu 2) Ich verstehe das als eine heuristische Vorgehensweise. Du denkst Dir einfach, daß von links eine ebene Welle einläuft, dann hast Du rechts davon eine nach rechts laufende ebene Welle (den transmittierten Teil) und links eine Überlagerung einer nach rechts laufenden ebenen Welle (dem einlaufenden Teil) und einer nach links laufenden ebenen Welle (dem reflektierten Teil).
Zu 3) Du solltest Dir bewußt machen, daß nicht-normierbare Zustände unphysikalisch und unmathematisch sind. Unphysikalisch, weil Du sie nicht probabilistisch interpretieren kannst, und unmathematisch, weil sie keinen Vektor im Hilbertraum darstellen (ein Skalarprodukt induziert immer eine Norm und eine Norm ist immer endlich). Sie sind ein Rechenhilfsmittel, um den Hamiltonoperator zu diagonalisieren, da man normierbare Zustände evtl. daraus linearkombinieren kann (z.B. ein Wellenpaket aus ebenen Wellen). Nicht weniger, aber auch nicht mehr. Für richtige L²-Lösungen der Schrödingergleichung kann man ein paar Regularitätseigenschaften beweisen. In drei Dimensionen gilt: Eigenfunktionen eines Hamiltonoperators für ein Potential, das sich als Summe eines quadratintegrablen und eines beschränkten Teils schreiben läßt (das ist für das Delta-Potential und den unendlich hohen Potentialtopf nicht der Fall, aber für alle anderen Potentiale, die mir spontan einfallen, schon), sind stetig und es gilt  \to 0) für für  (diese Eigenschaft folgt - anders, als manchmal leichtfertig behauptet wird - noch nicht aus der Quadratintegrierbarkeit; die Stetigkeit folgt auch noch nicht sofort daraus, daß der Zustand im Definitionsbereich des Laplace-Operators liegen muß, denn da wir es hier streng genommen nicht mit Funktionen, sondern mit Äquivalenzklassen davon zu tun haben [siehe Definition der Lebesgue-Räume], brauchen wir hier Differenzierbarkeit im distributionellen Sinn. Allerdings folgt sie daraus, daß die distributionelle Ableitung quadratintegrierbar sein soll, wie man mit ein paar Eigenschaften der Fouriertransformation zeigen kann; Ich bin gerne bereit, den übersichtlichen Beweis hier zu posten, wenn Du Dich dafür interessierst). (diese Eigenschaft folgt - anders, als manchmal leichtfertig behauptet wird - noch nicht aus der Quadratintegrierbarkeit; die Stetigkeit folgt auch noch nicht sofort daraus, daß der Zustand im Definitionsbereich des Laplace-Operators liegen muß, denn da wir es hier streng genommen nicht mit Funktionen, sondern mit Äquivalenzklassen davon zu tun haben [siehe Definition der Lebesgue-Räume], brauchen wir hier Differenzierbarkeit im distributionellen Sinn. Allerdings folgt sie daraus, daß die distributionelle Ableitung quadratintegrierbar sein soll, wie man mit ein paar Eigenschaften der Fouriertransformation zeigen kann; Ich bin gerne bereit, den übersichtlichen Beweis hier zu posten, wenn Du Dich dafür interessierst).
Streuzustände sind keine Lösungen der Schrödingergleichung in diesem Sinne und sie brauchen dementsprechend auch nicht im Unendlichen abzufallen. Für ebene Wellen ist das zum Beispiel nicht der Fall. Ich weiß allerdings nicht, ob man Aussagen über ihre Beschränktheit im Unendlichen formulieren kann.
Zu 4) Immer. Auch nicht normierbare Zustände entsprechen einem Spektralwert des Hamiltonoperators (Achtung: In der Funktionalanalysis ist Spektralwert nicht dasselbe wie Eigenwert, anders als in der linearen Algebra). Das Spektrum des Laplace-Operators befindet sich vollständig im negativen Teil der reellen Achse, d.h. kinetische Energien sind auch in der QM immer größer/gleich Null. |
|
 |
ph113
Anmeldungsdatum: 13.05.2016
Beiträge: 7
|
 ph113 Verfasst am: 13. Mai 2016 22:10 Titel: ph113 Verfasst am: 13. Mai 2016 22:10 Titel: |
 |
|
Hallo, erstmal vielen Dank für deine Antwort!
Ich hätte noch einige Fragen zu deiner Antwort:
Zu 1) Du sagst, dass es nicht immer so sein muss, dass Streuzustände nie normierbar sind und immer ein kontinuierliches Energiespektrum bzw. gebundene Zustände immer normierbar mit diskretem Energiespektrum sind. Ist das aber häufig der Fall? Warum definiert man gebundene Zustände und Streuzustände so wie ich angegeben habe über die Energie? Wenn man beispielsweise gefragt wird, für ein gegebenes Potential gebundene Zustände auszurechnen, ist dann immer gemeint, dass man die SE für E<0 lösen soll?
Kann man nichts Genaueres sagen, was ein gebundener Zustand oder ein Streuzustand denn nun ist, oder sind diese nur über das Vorzeichen der Energie definiert?
Zu 2) Wieso sind die Wahrscheinlichkeiten durch die einzelnen Amplituden gegeben? Ich verstehe nicht warum dieser Quotient die Wahrscheinlichkeit für Relfexion oder Transmission ist.
Zu 3) Das heißt, Streuzustände müssen nicht im unendlichen abfallen, aber kein Zustand darf im unendlichen divergieren, richtig?
Zu 4) Die Spektralwerte des Hamiltonoperators sind also immer positiv? D.h. wenn man ein freies Teilchen hat, muss E>0 gelten, richtig? Formal ist die SE für E <Vmin also nicht lösbar? |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 13. Mai 2016 22:52 Titel: Jayk Verfasst am: 13. Mai 2016 22:52 Titel: |
 |
|
1) Oh, entschuldigung, da habe ich mißverständlich geantwortet. Ich meinte, daß die nicht-normierbaren Zustände nicht unbedingt die mit E>0 sein müssen (und die norierbaren nicht die mit E<0). Wenn ich mich recht erinnere, ist es immer so, daß das kontinuierliche Spektrum den nicht-normierbaren Zuständen und das diskrete Spektrum den normierbaren Zuständen entspricht. Da müßte ich aber nochmal genau nachlesen, bevor ich hier was Falsches sage.
2) Ich denke nochmal darüber nach, ob mir eine bessere Antwort einfällt.
3) Ebene Wellen divergieren im Unendlichen (Divergenz heißt ja nur, daß es nicht konvergiert). Was Du meinst, ist wohl uneigentliche Konvergenz gegen Unendlich. Wie gesagt: Ich weiß nicht, ob man für nicht-normierbare Zustände entsprechende Aussagen treffen kann. Ich würde fast vermuten, daß dem nicht so ist.
4) Die Spektralwerte des freien Hamiltonoperators  sind immer nicht-negativ. Daraus, und aus der Tatsache, daß das Spektrum des Multiplikationsoperators V nach unten durch sind immer nicht-negativ. Daraus, und aus der Tatsache, daß das Spektrum des Multiplikationsoperators V nach unten durch  beschränkt ist, folgt, daß das Spektrum von beschränkt ist, folgt, daß das Spektrum von  ebenfalls nach unten durch ebenfalls nach unten durch  beschränkt ist, d.h. die stationäre Schrödingergleichung hat für niedrigere Energien keine Lösung. beschränkt ist, d.h. die stationäre Schrödingergleichung hat für niedrigere Energien keine Lösung. |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 14. Mai 2016 01:08 Titel: TomS Verfasst am: 14. Mai 2016 01:08 Titel: |
 |
|
Physikalisch würde man gebundene Zustände mit einem genügen schnellen Abfall der Wellenfunktion im Unendlichen assoziieren. Das funktioniert aber nicht immer, z.B. nicht für endliche Intervalle [a,b].
Der mathematisch präzise definierbare Unterschied resultiert aus dem diskreten, dem kontinuierlichen und den Rest-Spektrum.
In der QM hat man das Problem, dass man es zumeist mit nicht-beschränkten selbstadjungierten Operatoren zu tun hat. Damit sind einige Theoreme, die man aus der linearen Algebra für endlich-dimensionale Räume kennt, nicht mehr anwendbar.
Das Spektrum σ(T) eines Operators T auf einem Hilbertraum H besteht aus allen komplexen Zahlen λ, für die T − λ nicht invertierbar ist.
Man unterscheidet drei Fälle:
T − λ is ist nicht injektiv. Dies entspricht im wesentlichen der linearen Algebra; λ ist ein Eigenwert und gehört zum Punktspektrum von T.
T − λ ist injektiv, das Bild Im(T − λ) ist dicht in H, jedoch nicht ganz H; dicht bedeutet, der Abschluss von Im(T − λ) ist ganz H. Man spricht vom kontinuierlichen Spektrum.
T − λ ist injektiv, das Bild Im(T − λ) ist nicht dicht in H, d.h. der Abschluss von Im(T − λ) ist nicht ganz H. Man spricht vom Restspektrum.
Normale Operatoren, d.h. Operatoren die mit ihrem adjungierten Operator vertauschen, haben kein Restspektrum. Da in der QM immer selbstadjungierte Operatoren für Observablen vorausgesetzt werden, ist dieser letzte Fall in der QM irrelevant.
Häufig findet man die "Definition", dass Streuzustände nicht-normierbar seien. Dies entspricht in etwa der Aussage, dass Im(T − λ) dicht in H. Ganz passt das jedoch nicht zusammen. Z.B. können sowohl ebene Wellen als "verallgemeinerte Eigenfunktionen" des Impulsoperators als auch die Deltafunktionen als "verallgemeinerte Eigenfunktionen" des Ortsoperators durch quadratintegrable Funktionen angenähert werden; Operatoren haben ein reines kontinuierliches Spektrum. Allerdings würde man ebene Wellen als Steuzustände, Deltafunktionen wohl als Grenzfall gebundener Zustände bezeichnen.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
ph113
Anmeldungsdatum: 13.05.2016
Beiträge: 7
|
 ph113 Verfasst am: 14. Mai 2016 17:04 Titel: ph113 Verfasst am: 14. Mai 2016 17:04 Titel: |
 |
|
Danke nochmal für die Antworten.
Eine genaue Definition für gebundene Zustände und Streuzustände geht also die Definition über die Spektren? In einem Buch habe ich eine Definition gesehen, dass gebundene Zustände solche sind, in denen E kleiner als das Potential im Unendlichen auf beiden Seiten ist und Streuzustände solche, wo E größer als das Potential im Unendlichen auf einer Seite ist. Sind diese Definitionen äquivalent?
Mein Problem ist, dass ich wenn beispielsweise in einer Aufgabe steht "Berechnen Sie die Energien der gebundenen Zustände im Potential V=...", ich nicht weiß, nach welchen Energien ich nun suchen soll.
Ja sorry, mit divergieren meinte ich natürlich gegen unendlich gehen, also uneigentlich konvergiert. Solche Zustände müssen immer ausgeschlossen sein, oder?
In der Quantenmechanik Vorlesung sind wir noch nicht so weit und wir haben auch noch nicht viel Mathematisches gemacht. Werden deine Aussagen über die Spektren der Operatoren später noch behandelt?
LG |
|
 |
TomS
Moderator

Anmeldungsdatum: 20.03.2009
Beiträge: 18026
|
 TomS Verfasst am: 14. Mai 2016 17:41 Titel: TomS Verfasst am: 14. Mai 2016 17:41 Titel: |
 |
|
| ph113 hat Folgendes geschrieben: | | Eine genaue Definition für gebundene Zustände und Streuzustände geht also die Definition über die Spektren? |
Jein. Das Spektrum führt auf Eigenzustände oder deren Verallgemeinerungen. Aber physikalisch erlaubte Zustände müssen keine Eigenzustände sin.
| ph113 hat Folgendes geschrieben: | | In einem Buch habe ich eine Definition gesehen, dass gebundene Zustände solche sind, in denen E kleiner als das Potential im Unendlichen auf beiden Seiten ist und Streuzustände solche, wo E größer als das Potential im Unendlichen auf einer Seite ist. Sind diese Definitionen äquivalent? |
Nein, sind sie im Allgemeinen nicht.
Zum einen setzen Sie ein sehr spezielles Potential voraus. Was wäre z.B. mit einem sinusförmgen Potential? Zum anderen müssen Zustände keine Eigenzustände sein. D.h. eine Summe aus gebundenen Eigenzuständen wäre immer noch ein gebundener Zustand, jedoch kein Eigenzustand.
Der Sprachgebrauch der Physiker ist leider oft schlampig.
| ph113 hat Folgendes geschrieben: | | Mein Problem ist, dass ich wenn beispielsweise in einer Aufgabe steht "Berechnen Sie die Energien der gebundenen Zustände im Potential V=...", ich nicht weiß, nach welchen Energien ich nun suchen soll. |
Wenn kein "pathologisches" Potential vorliegt, dann nach solchen, deren Energie kleiner ist als das als im Unendlichen konstant angenommene Potential; da ist der Sprachgebrauch ausreichend.
| ph113 hat Folgendes geschrieben: | | Werden deine Aussagen über die Spektren der Operatoren später noch behandelt? |
In einer guten Vorlesung wird zumindest darauf hingewiesen, dass die notwendige Mathematik recht aufwändig, die Darstellung der Physiker jedoch unsauber ist.
Zumeist solltest du damit klarkommen, dass mit "gebundenen Zuständen" soetwas gemeint ist wie
 = V_\infty)

 \sim e^{-\kappa |x|})
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
 |
|
|















