| Autor |
Nachricht |
Teilchen
Gast
|
 Teilchen Verfasst am: 26. März 2016 14:39 Titel: gekrümmter Hilbertraum |
 |
|
Hallo
mir ist grad etwas eingefallen und wollte fragen, ob es bereits Anwendungen für sowas gibt und zwar habe ich mich mit der Beschreibung gekrümmter Räume beschäftigt wie sie in der allgemeinen Relativitätstheorie verwendet werden.
Jetzt könnte man doch auch einen gekrümmten Hilbertraum einführen mit einer verallgemeinerten riemannschen Metrik. Ich betrachte dazu eine Kurve in dem Hilbertraum und parametrisiere diese Kurve mit einem Parameter  so dass sie durch  \in H) dargestellt wird.
Eine mögliche Metrik eines gekrümmten Hilbertraums wäre meiner Meinung nach lokal durch
}{\partial t}|g\frac{\partial \phi(t)}{\partial t}\rangle dt^2)
gegeben, wobei 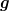 ein metrischer Tensoroperator ist.
Wäre dies ein in sich konsistentes Objekt und findet es irgendwo in der Physik Anwendung?
Ich beschäftige mich mit der Differentialgeometrie im Allgemeinen und tue mich schwer mit vielen Definitionen. Ich merke, dass die Definitionen auf etwas sehr Anschaulichem basieren, aber es wird so abstrakt formuliert, dass es mir schwer fällt es nachzuvollziehen, auch merke ich, dass ich es in dieser Abstraktheit nicht verstehen muss, um damit in der Physik zu arbeiten. Zum Beispiel verstehe ich die Wikipedia-Definition von Differentialformen nicht ganz, habe aber trotzdem ein Verständnis von Differentialformen und kann mit ihnen arbeiten. Jetzt frage ich mich, ob es überhaupt zu einem besseren Verständnis der Physik führt, wenn man die Mathematik auf Mathematikerniveau behandelt. Zum Beispiel sind Tensoren für mich über ihr Transformationsverhalten definiert, während Mathematiker Tensoren darstellungsunabhängig definieren, was dann aber dazu führt, dass ich die Definitionen schwerer nachvollziehen kann. |
|
 |
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 26. März 2016 17:19 Titel: |
|
|
Ich verstehe deine Formel nicht.
Wenn dein Hilbertraum ein Funktionenraum in einer Variable x sein soll, dann wäre ein entsprechendes Skalaprodukt gegeben durch
\,v(x))
Die Norm eines Vektors wäre dann
Eine Metrik würde einen Abstandsbegriff bedeuten. Der Abstand wäre dann soetwas wie
 = ||u - v||)
Ich kann nun deine Formel nicht zu einem Hilbertraum in Beziehung setzen.
Meinst du eine Kurve auf eine gekrümmten, Riemannschen Mannigfaltigkeit?
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
Teilchen
Gast
|
| Teilchen Verfasst am: 26. März 2016 19:05 Titel: |
|
|
Hallo Tom
Ich wende mal meine Formel auf ein Beispiel an damit ihre Bedeutung klarer wird.
Ich betrachte den Hilbertraum eines Spin-1/2-Teilchens. In z-Darstellung kann ich den Spinzustand als zwei-komponentigen Vektor =(\chi_1(t), \chi_2(t))) schreiben und g wird dann zu einer 2x2 Matrix mit den zustandsabhängigen Komponenten.
, \chi_j(t))) . In meine Formel eingesetzt ergibt dies.
}{\partial t}\frac{\partial \chi^{j}(t)}{\partial t}dt^2) mit Einsteinscher Summenkonvention.
In der Standardquantenmechanik ist nun 
Damit folgt:
}{\partial t}\frac{\partial \chi^{j}(t)}{\partial t}dt^2)
Die Variationsrechnung zeigt, dass der Weg zwischen zwei Zuständen ) und ) minimal ist, wenn
}{\partial t}=a \quad \text{und} \quad \frac{\partial \chi^{2}(t)}{\partial t}=b) , wobei a und b konstanten sind.
Dann folgt:
}{\partial t}\frac{\partial \chi^{1}(t)}{\partial t}+\frac{\partial \chi^{* 2}(t)}{\partial t}\frac{\partial \chi^{2}(t)}{\partial t}}dt=\int \limits_{t_0}^{t_1}\sqrt{a^2+b^2}dt=\sqrt{a^2+b^2}(t_1-t_0)=\sqrt{(a(t_1-t_0))^2+(b(t_1-t_0))^2})
-\chi^1(t_0))^2+{(\chi^2(t_1)-\chi^2(t_0))^2}})
Letzteres entspricht der üblichen Metrik, wie du sie auch angeschrieben habe. Ich hoffe, dass es durch dieses Beispiel klarer geworden ist. Nun kann man aber die g_{ij} als zustandsabhängige Funktionen betrachten. Ich wollte halt versuchen die Konzepte des riemannschen Raumes auf den Hilbertraum der Quantenmechanik zu übertragen und ihn so zu verallgemeinern. Meine Frage ist, ob meine Vorgehensweise logisch konsistent ist und ob sowas bereits gemacht wurde bzw. ob soetwas irgendwo eine Anwendung hat oder haben könnte. |
|
|
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
| Jayk Verfasst am: 27. März 2016 01:23 Titel: |
|
|
|
@Teilchen: Wenn Du einen sanften Einstieg in die Differentialgeometrie im Allgemeinen und Differentialformen im Speziellen suchst, kann ich Dir das Büchlein "Vektoranalysis" von Klaus Jänich wärmstens empfehlen! Dort wird sehr viel Wert auf die Anschauung gelegt. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 27. März 2016 10:06 Titel: |
|
|
Du rechnest schon richtig, allerdings ist das Konzept des Linienelementes entlang der Trajektorien bzw. deren Längen im Zustandsraum für die QM irrelevant.
Betrachten wir mal allgemein die Zeitentwicklung eines quantenmechanischen Zustandsvektors
\,|\psi,t_0\rangle)
 = e^{-iH(t-t_0)})
D.h. die Trajektorie für jedes quantenmechanische System mit Hamiltonoperator H ist definiert durch die Schrödingergleichung bzw. den Zeitentwicklungsoperator U.
Schauen wir uns mal in der ART an, wie man auf das Linienelement kommt
Das kann man schreiben als
d.h. der metrische Tensor bzw. seine Komponenten treten auf bzgl. bestimmter Basisvektoren.
In der QM können wir die Zeitableitung eines Zustandes mittels der Schrödingergleichung bzw. mittels des o.g. Zeitentwicklungsoperators explizit berechnen:
Damit gilt
Die so definierte "Länge" lautet dann
Mir ist nicht bewusst, dass dieses Matrixelement bzw. diese "Länge" irgendwo Verwendung finden.
Einführen von Basisvektoren entspricht dem Einschieben der Eins
Wählen wir speziell die Eigenbasis zu H, so folgt für das Linienelement
sowie für die so definierte "Länge"
Betrachten wir zuletzt einen normierten Energieeigenzustand |E>
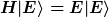
Damit folgt für das Integral
)
Das entspricht gerade der Wirkung S entlang der klassischen Trajektorie. Diese wird jedoch i.A. anders definiert. Es ist ein Zufall, dass gerade ein Energieeigenzustand vorliegt und für diesen eine entsprechende Vereinfachung des Integrals möglich ist. I.A. würde man andere Integrale ansetzen.
M.E. sind diese Formeln im Rahmen der QM völlig irrelevant.
Ich habe oben keine "Metrik" bzgl. der Basis |n> eingeführt; m.E. ist das auch nicht zulässig, wenn man die Basis |n> als Orthonormalbasis ansetzt und darin die Vollständigkeitsrelation formuliert; würde man diese Gleichung modifizieren, so läge kein Hilbertraum mehr vor.
In Diagonalform entspräche dies
Quadrieren führt auf
und damit zwingend
Der einzige - mir bekannte - Anwendungsfall im Rahmen der QM für Trajektorien in einer nicht-trivialen Geometrie ist die sogenannte Berry-Phase; dabei betrachtet man jedoch nicht den Hilbertraum sondern den Parameterraum eines Systems. Das kannst du du mal anschauen; ist recht eng verwand mit deiner Betrachtung von differenzierbaren Mannigfaltigkeiten und sowohl mathenatische als auch physikalisch interessant.
Die letzte Rechnung führt auf die Wirkung für ein freies Teilchen. Die Wirkung spielt im Rahmen der Pfadintegralquantisierung eine wichtige Rolle. Allerdings wird ein völlig anderer Formalismus verwendet; eine Metrik oder Krümmung auf dem Hilbertraum liegt wiederum nicht vor.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago.
Zuletzt bearbeitet von TomS am 27. März 2016 21:21, insgesamt 2-mal bearbeitet |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 27. März 2016 10:16 Titel: |
|
|
Noch ein Nachtrag.
Die Bedeutung der minimalen Länge einer Trajektorie (Geodäte) in der ART folgt ja aus dem Prinzip der minimalen Wirkung
Man kann die Schrödingergleichung ebenfalls aus einem Wirkungsfunktional ableiten:
Ich sehe nicht, wie man über diese Darstellung zu einer Art "Metrik" im Hilbertraum gelangen könnte.
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18049
|
| TomS Verfasst am: 27. März 2016 12:00 Titel: |
|
|
Ein zweiter Nachtrag.
In der QM werden Zustandsvektoren als normierte Hilbertraumvektoren dargestellt, d.h. sie "leben" auf einer unendlich-dimensionalen Einheitskugel
Damit könnte man natürlich die intrinsische Krümmung dieser Einheitskugel betrachten, die jedoch in einen flachen Raum eingebettet ist. Ein Abstandsbegriff auf dieser Kugel folgt trivialerweise mittels
 = \alpha_{u,v})
_________________
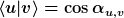
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
|
|
Registrieren
Login
FAQ
Suchen
