| Autor |
Nachricht |
Berni1970
Gast
|
 Berni1970 Verfasst am: 01. Nov 2015 14:48 Titel: Wenn der Mond still steht |
 |
|
Meine Frage:
Als ich neulich mit Freunden am Abend unterwegs war, hieß es da: "Der Mond steht so schön am Himmel". Ich sagte dann, dass er nicht "stehe", sonst fiele er uns nämlich bald auf den Kopf.
Daraufhin kam die Frage auf, wie lange es denn dauern würde, bis der Mond hier sei und ich dachte, das ließe sich bestimmt leicht berechnen, da ja aus Erd- und Mondmasse, sowie der Entfernung die Gravitation ermittelbar ist. Entfernung, meinetwegen auch abzüglich der Radien, sind ja auch bekannt. Die Ausgangssituation wäre dann so, dass der Mond und die Erde in 384400 km Entfernung, ohne Eigenbewegung losgelassen, und nur durch ihre eigene, wechselseitige Schwerkraft aufeinander zu stürzen würden.
Leider bin ich nicht so schlau, wie ich dachte, denn obwohl ich schon das ganze Wochenende herumprobiere und suche, finde ich keine passende Formel dazu.
Das Problem ist, dass die Gravitation und damit ja die Beschleunigung bei fortschreitender Annäherung zunimmt, also eben nicht gleichmäßig beschleunigt werden dürfte. Außerdem bin ich nicht sicher, inwieweit die Massenträgheit hier zum Tragen kommt.
Meine Ideen:
Ich habe versucht, den Vorgang zu zerlegen und habe kleinere Zeitabschnitte von 10 oder 100 Sekunden betrachtet und v(t), s(t) und die verbleibende Distanz schrittweise mit den üblichen, newtonschen Formeln betrachtet, aber ich muss irgendwas grundsätzliches falsch gemacht haben. Die Beschleunigung, läge demnach z.B. immer bei 0,0027 m/s^2 und nimmt nicht wesentlich zu. Und selbst wenn ich es so hinbekommen hätte, ist es doch eher eine Näherung. Ich hätte gerne gewusst, wie man es richtig macht.
Kann mir jemand sagen, nach welchem Begriff ich suchen muss? Gibt es eine einigermaßen verständliche Quelle, aus der ich das Nötige lernen kann, oder ist es am Ende eine ganz einfache Formel? |
|
 |
Duncan
Gast
|
| Duncan Verfasst am: 01. Nov 2015 15:04 Titel: |
|
|
Das ist ganz einfach:
stell dir vor, die Bahnellipse würde immer flacher und flacher werden, bis der Mond in einer entarteten Ellipse (um den gemeinsamen Schwerpunkt Erde Mond) rotiert (=pendelt).
Seine Umlaufzeit bleibt dabei gleich (siehe Kepler). |
|
|
Berni1970
Gast
|
| Berni1970 Verfasst am: 01. Nov 2015 16:30 Titel: |
|
|
Ja, natürlich  - da hätte ich wirklich selber drauf kommen können.
Was übrig bleibt ist eine einfache Pendelbewegung, auf der man die Positionen und Zeitpunkte genau ermitteln kann.
Vielen Dank! |
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 01. Nov 2015 17:25 Titel: |
|
|
| 3. Keplergesetz hat Folgendes geschrieben: | | Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die Kuben der großen Bahnhalbachsen. |
Also
^2 = \left( \frac{384000\ km}{2\cdot 384000\ km} \right)^3 = 1/8 )
Daraus Fallzeit = 5,95 Tage
Stimmt das?
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
Berni1970
Gast
|
| Berni1970 Verfasst am: 02. Nov 2015 09:43 Titel: |
|
|
Ja, das müsste grob stimmen. Allerdings wäre das die Zeit bis zum Durchgang des Mondes durch das gemeinsame Massezentrum. Das Auftreffen des Mondes auf die Erdoberfläche ist etwas früher. Die Radien beider Himmelskörper müssen abgezogen werden und die Erde kommt dem Mond in der Zeit ja auch noch etwas entgegen.
Wenn man es genau wissen will, muss man also doch etwas mehr rechnen. |
|
|
borromeus
Anmeldungsdatum: 29.12.2014
Beiträge: 509
|
| borromeus Verfasst am: 02. Nov 2015 13:20 Titel: |
|
|
| isi1 hat Folgendes geschrieben: | | 3. Keplergesetz hat Folgendes geschrieben: | | Die Quadrate der Umlaufzeiten zweier Planeten verhalten sich wie die Kuben der großen Bahnhalbachsen. |
Also
Daraus Fallzeit = 5,95 Tage
Stimmt das? |
Isi1, kannst Du erläutern wie Du zu den Werten in dieser Formel kommst? |
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 02. Nov 2015 15:41 Titel: |
|
|
| borromeus hat Folgendes geschrieben: | | Isi1, kannst Du erläutern wie Du zu den Werten in dieser Formel kommst? |
Ich hab doch nur "Kepler 3" aufgeschrieben (siehe zitierten Text).
Vielleicht die Maße zur Ellipse:
Durchmesser Mondbahn 2 * 384000 km = Große Achse der zum Kreis entarteten Ellipse
Große Achse der ganz flach gequetschten entarteten Ellipse beim freien Fall 384000 km. Man denkt sich eine Ellipse, die in vielleicht 1 cm Abstand um den Erdmittelpunkt verläuft - natürlich müssten die Massen der Erde und des Mondes dann zum "Schwarzen Loch" degeneriert sein - da hätte sie 8 mm und der Mond ein Zehntel mm Schwarzschildradius.
Umlaufzeit des Mondes 28 Tage
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
borromeus
Anmeldungsdatum: 29.12.2014
Beiträge: 509
|
| borromeus Verfasst am: 02. Nov 2015 18:16 Titel: |
|
|
Und warum 2x Fallzeit?
Was soll das für eine Zeit sein?
Und warum sind jeweils im Nenner 28 Tage und 2x384000 km.
"Der", mit den 28 Tagen ist ja nur 384000km entfernt.
Edit: jetzt dämmertst. der Brennpunkt der flachen Ellipse liegt im Systemschwerpunkt, also in der Erde.
stimmt das? |
|
|
isi1
Anmeldungsdatum: 03.09.2006
Beiträge: 2902
Wohnort: München
|
| isi1 Verfasst am: 02. Nov 2015 22:28 Titel: |
|
|
| borromeus hat Folgendes geschrieben: | Und warum 2x Fallzeit?
Was soll das für eine Zeit sein? |
Ist doch klar, die Fallzeit ist die Hälfte einer vollen Umrundung.
| borromeus hat Folgendes geschrieben: | Und warum sind jeweils im Nenner 28 Tage und 2x384000 km.
"Der", mit den 28 Tagen ist ja nur 384000km entfernt. |
Ja genau, deshalb ist der volle Durchmesser der normalen Mondbahn doppelt so groß.
| borromeus hat Folgendes geschrieben: | Edit: jetzt dämmertst. der Brennpunkt der flachen Ellipse liegt im Systemschwerpunkt, also in der Erde.
stimmt das? |
Ja, der eine Brennpunkt, der andere ist am höchsten Punkt der Mondbahn. Das liegt daran, dass die Ellipse zu einem Strich entartet ist, da sind die Brennpunkte jeweils am Ende des Strichs.
_________________
Grüße aus München, isi •≡≈ ¹₁₂½√∠∞±∫αβγδεηκλπρσφω ΔΣΦΩ |
|
|
xb
Gast
|
| xb Verfasst am: 02. Nov 2015 23:27 Titel: |
|
|
man setzt ja die große Bahnhalbachse ein
deshalb ist das vielleicht etwas deutlicher
^2 = \left( \frac{\frac{1}{2 }\cdot 384000\ km}{384000\ km} \right)^3 = 1/8 ) |
|
|
Gregor
Gast
|
| Gregor Verfasst am: 27. Nov 2015 22:42 Titel: |
|
|
|
Hä? Das kann doch nicht stimmen, oder? Der Mond wird doch nicht gleichmäßig beschleunigt, wenn er sich der Erde nähert. Die Erdanziehung nimmt doch mit abnehmender Entfernung zu. Die Amplitude der Schwingung mag gleich bleiben, aber die Zeit, bis er hier ist müsste doch kürzer sein, weil die Beschleunigung, anders als beim normalen Umlauf zunimmt? |
|
|
E=mc²
Anmeldungsdatum: 24.06.2014
Beiträge: 494
|
| E=mc² Verfasst am: 27. Nov 2015 23:33 Titel: |
|
|
| Gregor hat Folgendes geschrieben: | | Hä? Das kann doch nicht stimmen, oder? Der Mond wird doch nicht gleichmäßig beschleunigt, wenn er sich der Erde nähert. Die Erdanziehung nimmt doch mit abnehmender Entfernung zu. Die Amplitude der Schwingung mag gleich bleiben, aber die Zeit, bis er hier ist müsste doch kürzer sein, weil die Beschleunigung, anders als beim normalen Umlauf zunimmt? |
Da Kepler elliptische Bahnen betrachtet und bei diesen der Abstand zwischen Zentralmasse und Umlaufkörper im allgemeinen nicht konstant ist, ist eben dieser Ansatz geeignet, um das Problem zu lösen, dass die Gravitationskraft nicht immer gleich groß ist und man sich keine komplizierte Rechnung eintreten will. |
|
|
TomS
Moderator
Anmeldungsdatum: 20.03.2009
Beiträge: 18029
|
| TomS Verfasst am: 28. Nov 2015 01:11 Titel: |
|
|
Wir haben das Problem hier schon mal diskutiert. Der Ansatz mittels "Kepler" ist nicht so offensichtlich, wie es zunächst erscheinen mag. Ich habe eine Alternative zu diesem Lösungsweg vorgeschlagen.
http://www.physikerboard.de/topic,31833,-erde-stuerzt-in-die-sonne.html
_________________
Niels Bohr brainwashed a whole generation of theorists into thinking that the job (interpreting quantum theory) was done 50 years ago. |
|
|
lampe16
Anmeldungsdatum: 21.03.2010
Beiträge: 319
|
| lampe16 Verfasst am: 28. Nov 2015 23:17 Titel: |
|
|
Zum Vergleich mit den hier genannten Zahlenwerten habe ich das Zweimassen-Zustandsraummodell (Großbuchstaben: Erde, Kleinbuchstaben: Mond)
G\frac{mM}{a^2})
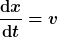
mit den Anfangswerten
=384000{\rm \,\,km} )
=X(0)=V(0)=0)
und den Konstanten
durchgerechnet.
Damit ergibt sich nach  und  .
Was noch interessant ist: Wenn man sich die Kollision als kräftefreie Durchdringung vorstellt, wendet der Mond bei dem Modell "Strichellipse", wie es TomS erläutert, in der Erde (=Perihel) bei Erhaltung des Geschwindigkeitsbetrags um 180° und läuft zum Ausgangspunkt (=Aphel) zurück, wo er mit der Geschwindigkeit null ankommt. Dem von mir verwendeten Modell entspricht eine ganz andere Bahn: Der Mond durchdringt die Erde ohne Kehrtwendung und schwingt auf gerader Bahn weiter bis ) , um erst dort wieder umzukehren. Die Schwingung hat die doppelte Weite.
Beide Modelle führen zur selben Fallzeit.
_________________
Herzliche Grüße, Lampe16
_________________________________________
Hard work beats talent if talent doesn't work hard. |
|
|
|
Registrieren
Login
FAQ
Suchen
