| Autor |
Nachricht |
mathilope
Anmeldungsdatum: 26.06.2015
Beiträge: 6
|
 mathilope Verfasst am: 29. Jun 2015 19:53 Titel: Spektralsatz auf unendlich dimensionalen Hilberträumen mathilope Verfasst am: 29. Jun 2015 19:53 Titel: Spektralsatz auf unendlich dimensionalen Hilberträumen |
 |
|
Meine Frage:
In der Quantenmechanikvorlesung, die ich besuche, wurde ein eher intuitiver Ansatz gewählt. Hilberträume und die Diracschreibweise wurden erstmal in endlicher Dimension eingeführt und dann aber ohne das groß zu erwähnen auf unendlichdimensionale Fälle ausgeweitet. Ich habe mich dann an ein anderes Skript gehalten, was etwas mathematischer und präziser an die Sache rangeht und viele interessante Punkte anspricht, die in unserer Vorlesung komplett übergangen wurden, bspw. dass es physikalisch wesentlich ist, dass eine Wellenfunktion, die ein QM-System löst im Definitionsbereich des dazugehörigen Operators liegen muss und diese Operatoren im Allgemeinen gar nicht auf dem gesamten HR definiert sind! (Bsp. war hier der Hamiltonop. des H-Atoms)
Meine Ideen:
Tenor in allen mir bekannten Quellen war, dass man sich grundsätzlich nur um separable Hilberträume (ich kürze Hilbertraum nun HR und den Plural HR:e ab) zu kümmern braucht, also solche, in denen ein höchstens abzählbares Orthonormalsystem (ONS pl. ONS:e) enthalten ist.
Sei also  ein Hilbertraum, der ein ONS ein Hilbertraum, der ein ONS  umfasst. Sei die Indesmenge I von abzählbar unendlicher Kardinalität. Dann ist umfasst. Sei die Indesmenge I von abzählbar unendlicher Kardinalität. Dann ist  unendlich-dimensional. unendlich-dimensional.
Frage an dieser Stelle:
Kann  auch unendlich dimensional sein, wenn er eben kein unendliches ONS (bzw. später ONB) besitzt, sondern nur ein endliches? auch unendlich dimensional sein, wenn er eben kein unendliches ONS (bzw. später ONB) besitzt, sondern nur ein endliches?
Es gelte zudem für f in  : :

es existiere also kein Vektor, außer dem Nullvektor, der auf  orthogonal steht, man nennt orthogonal steht, man nennt  dann eine ONB von dann eine ONB von  . Es folgt direkt, dass damit alle ONB:en von . Es folgt direkt, dass damit alle ONB:en von  dieselbe Mächtigkeit besitzen und wir ordnen dem Hilbertraum die Mächtigkeit der ONB als Dimension zu. Im abzählbar unendlichen Fall ist das dieselbe Mächtigkeit besitzen und wir ordnen dem Hilbertraum die Mächtigkeit der ONB als Dimension zu. Im abzählbar unendlichen Fall ist das  . .
Der bis hierhin definierte HR ist also separabel. Ein Bsp. dafür ist der  ) (für einen d-dim:en Positionsraum). Und der ist ja auch physikalisch besonders relevant (lösungen des harmonischen Oszillators liegen ja z.B, darin, oder? Ich habe zudem auf wikipedia gelesen, dass sogar alle separablen HR:e isomorph sind zu (für einen d-dim:en Positionsraum). Und der ist ja auch physikalisch besonders relevant (lösungen des harmonischen Oszillators liegen ja z.B, darin, oder? Ich habe zudem auf wikipedia gelesen, dass sogar alle separablen HR:e isomorph sind zu  ) (also alle sep:en HR:e sind isomorph zu (also alle sep:en HR:e sind isomorph zu  ) darunter auch darunter auch  ) ). Jetzt ist aber die Wellenfunktione des freien Teilchens, also Eigenfunktionen des Hamiltonoperators ). Jetzt ist aber die Wellenfunktione des freien Teilchens, also Eigenfunktionen des Hamiltonoperators

nicht quadratintegrierbar (also nicht in  ) ), denn: ), denn:

{Reichen nun die separablen Hilberträume doch nicht aus, um die handelsüblichen Probleme der QM zu betrachten? Ihr seht meine Vewirrung.}
Nunja weiter im Text.
Man kann weiterhin feststellen, dass für jeden HR (somit auch für separable) in jedem Fall (weil es sich um Eigenschaften des inneren Produkts handelt) gilt:
(i) der Satz des Pythagoras
fuer alle orthogonalen Projektoren P und jedes  gilt: gilt:

(ii) Bessel'sche Ungleichung
wenn die  ein ONS bilden, gilt: ein ONS bilden, gilt:
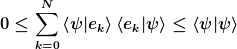
Nach meinem Dafürhalten wäre hier allerdings auch ein ONS unendlicher Dimension erlaubt, ich würde das so schreiben:
Sei  eine ONB. Wenn eine ONB. Wenn  ein ONS bilden, gilt: ein ONS bilden, gilt:

und weiter
(iii) Parsevalsche Gl.
Wenn  eine ONB ist, gilt: eine ONB ist, gilt:

Da ist dann schon eine Zerlegung der Identität bzgl. einer Basis enthalten, also es steht ja da:
 \left| \psi \right> = \sum\limits_{k \in I} \left< \psi | e_k \right> \left< e_k | \psi \right> = \sum\limits_{k \in I} | \left< e_k | \psi \right> |^2 )
oder bin ich da zu voreilig, weil es eben nicht so leicht ist die Eins zu zerlegen? Bei einer ggb:en Basis stimmt das aber doch, oder?
Der springende Punkt ist dann wohl, ob sich ein Operator in eine ONB aus Eigenvektoren hergibt, in die sich dann eine Identität oder er selbst zerlegen lässt.
Grundsätzlich stellt sich wohl das Problem, dass ein Operator nicht mehr auf dem ganzen unendl. dim:en HR definiert ist (und operiert) sondern nur auf Teilräumen. Das war vorher nicht so, wir konnten ja den Operator in den Eigenbasen anderer Operatoren darstellen, die denselben ganzen endlichen Hilbertraum auspannten. Da dann Operatoren auf dem ganzen HR definiert waren, ergaben sich Probleme (Stetigkeit, Beschränkheit; was bedeutet Selbstadjungiertheit;...) nicht. Es waren immer alle Operatoren stetig, weil beschränkt. Das ist nun nur noch zwangsläufig für Operatoren der Fall, die ebenfalls auf dem ganzen unendlich dim:en HR def. sind.
(bei dieser Aussage bin ich mir nicht sicher, die ist auch aus dem Skript. Gilt das vielleicht nur für symmetrische Operatoren? Also Def:bereich ganz H + symm. => stetig ? Die abgeschwächte Aussage ist aus der Wikipedia, auch hierzu habe ich eine Frage. Da wir uns in komplexen Hilberträumen bewegen, ist dann nicht eher hermite'sch statt symmetrisch gemeint? ).
Es ist aber die Regel, dass Operatoren, die nur auf Teilräumen def. sind, eben nicht stetig sind. Man sollte also einmal zwischen stetigen und nicht stetigen (beschränkten und nicht beschränkten) Operatoren unterscheiden.
Ebenfalls wichtig ist die Frage ob der Definitionsbereich von einem Operator dicht im Hilbertraum liegt, sonst kommt es wohl zu Problemen bei der Definition des Adjungierten. Und da wir ja letztlich häufig (immer? Oder gibt es auch andere interessante Fälle) auf Observablen hinauswollen, die durch selbstadjungierte (impliziert ein Adjungiertes) Operatoren dargestellt werden, ist das wichtig.
Ich möchte nun wieder ordentlich definieren:
Sei A ein Operator mit Domäne  dicht-definiert in dicht-definiert in  , also , also  . .
Dann ist der adjungierte Operator  auf einer Domäne auf einer Domäne  definiert. definiert.
Liegt diese ebenfalls dicht in  so heißt A abschließbar und es gilt: so heißt A abschließbar und es gilt:
 und und 
wobei  den Abschluss von A selbst bezeichnet. Im allgemeinen gilt dabei: den Abschluss von A selbst bezeichnet. Im allgemeinen gilt dabei: 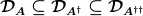
Machen wir jetzt den Schritt zum selbstadjungierten Operator:
Gilt insbesondere:
(i) Gleichheit der Definitionsbereiche:

(ii) und Hermitizität:

so ist A selbstadjungiert.
Jetzt habe ich auch hier direkt eine Frage: Ist die Gleichheit der Definitionsbereiche auch schon gleichbedeutend damit, dass A abgeschlossen ist?
Denn es ist  dichtdefiniert und damit dichtdefiniert und damit 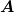 abschließbar. Umgekehrt ist dann abschließbar. Umgekehrt ist dann  und damit dicht definiert, d.h. auch und damit dicht definiert, d.h. auch  ist abschließbar mit ist abschließbar mit  d.h. d.h.  ist bereits abgeschlossen. Ebenso ist ist bereits abgeschlossen. Ebenso ist  Wir haben also Wir haben also  und für mich naheliegend wäre und für mich naheliegend wäre  Ich schaffe es aber nicht, das zu zeigen ohne die Hermitizität von A vorauszusetzen. Hat jemand eine Idee? Ich kann natürlich auch zeigen, dass für den selbstadjungierten Operator Ich schaffe es aber nicht, das zu zeigen ohne die Hermitizität von A vorauszusetzen. Hat jemand eine Idee? Ich kann natürlich auch zeigen, dass für den selbstadjungierten Operator  gilt: gilt:
 Aber das hilft mir noch nicht, weil ich im Allgemeinen keine Invertierbarkeit von Aber das hilft mir noch nicht, weil ich im Allgemeinen keine Invertierbarkeit von  habe. habe.
Für selbstadjungierte A sind wir auf jeden Fall schon sehr nahe an einem Spektralsatz dran. Wir müssen aber erst noch ein Spektrum definieren und schauen, wie das aussieht.
Sei A ein Operator über einem Hilbertraum. Die Resolvente vom Operator A und einer Zahl  ist definiert als ist definiert als
=(z \mathbb I -A)^{-1} ) . .
Die Resolventenmenge  ist def. als ist def. als
 \text { ist stetig} \} = \{ z \in \mathbb{C} | (z \mathbb I -A) \text{ ist beschränkt invertierbar} \})
Das Spektrum ist als deren Komplement definiert
 = \mathbb{C} \setminus \mathcal{R} _{A} )
und kann unterteilt werden in einen diskreten Anteil
 = \{ (\lambda \in \mathbb C | ( \lambda \mathbb I - A) \text {ist nicht invertierbar} \} = \{ \lambda \in \mathbb{C} | \lambda \text{ ist Eigenwert von }A \} )
und einen kontinuierlichen Anteil
 = \{ \lambda \in \mathbb{C} | ( \lambda \mathbb{I} - A )^{-1} \text{ existiert, aber ist nicht stetig.} \} )
Kommen wir nun zum Spektralsatz:
Sei  ein unendlich dimensionaler Hilbertraum. ein unendlich dimensionaler Hilbertraum.  ein dichter Teilraum auf dem A dicht-definiert ist. ein dichter Teilraum auf dem A dicht-definiert ist.
(i) A sei selbstadjungiert und  ) sei für abzählbar viele sei für abzählbar viele 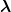 nicht invertierbar, aber sonst beschränkt invertierbar. nicht invertierbar, aber sonst beschränkt invertierbar.
Dann ist das Spektrum  = \{ \lambda _j \}_{j \in J} ) mit einer Indexmenge J der Kardinalität mit einer Indexmenge J der Kardinalität  reell und die reell und die  Eigenwerte von Eigenwerte von 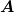 . Die zu den verschiedenen . Die zu den verschiedenen 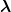 korresponierenden Eigenvektoren bilden eine ONB korresponierenden Eigenvektoren bilden eine ONB  von von  und geben eine Spektralzerlegung für und geben eine Spektralzerlegung für 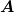 und und  in der Form: in der Form:

und

und für den Hilbertraum  in der Weise: in der Weise:
 } )
(ii) A sei selbstadjungiert und  ) sei für abzählbar viele sei für abzählbar viele 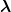 nicht invertierbar, aber sonst (nicht notwendigerweise beschränkt) invertierbar. nicht invertierbar, aber sonst (nicht notwendigerweise beschränkt) invertierbar.
Dann ist das Spektrum  ) reell und zerfällt in einen diskreten und kontinuierlichen Anteil reell und zerfällt in einen diskreten und kontinuierlichen Anteil
 = \sigma _d (A) + \sigma _c (A) )
wobei gilt
(ii.1)  = \{ \lambda _j \}_{j \in J} ) mit einer Indexmenge J der Kardinalität mit einer Indexmenge J der Kardinalität  enthält Eigenwerte enthält Eigenwerte  von von 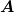 . Sie bilden ein korrespondierendes ONS . Sie bilden ein korrespondierendes ONS  , das keine ONB von , das keine ONB von  ist. ist.
(ii.2) Es können Intervalle 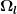 gefunden werden, s.d. gefunden werden, s.d.  = \cup _{l \in L} \Omega _l ) mit einer Indexmenge der Kardinalität mit einer Indexmenge der Kardinalität  , auf denen , auf denen  ) für alle für alle  invertierbar ist, aber nicht beschränkt invertierbar. invertierbar ist, aber nicht beschränkt invertierbar.
Es gibt dann eine Zerlegung der Operatoren  und und 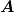 in der Form in der Form

und

mit projektorwertigen Elementen E_\lambda der Spektralschar zum zu A eindeutig bestimmten Spektralmaß E.
(Stimmt das so? Ich habe wirklich nicht viel Ahnung von Spektralmaßen, eigentlich weiß ich nicht genau, was hier Spektralmaß ist, was Träger, was Spektralschar und ob die Schreibweise des Integrals stimmt und sinnig ist, weiß ich auch nicht. Hier brauche ich wirklich Hilfe.)
und des Hilbertraums:
Wie schreibe ich das? Mit einem stetigen und nicht stetigen Kern und dem span vom ONS?
Dann gibt es ja noch weitere Sonderfälle von Operatoren, die werden aber hauptsächlich in der Mathe verwendet oder? Lohnt es sich überhaupt zwischen (allesamt selbstadjungierten) beschränkten, kompakten und allgemeinen Operatoren zu unterscheiden (aus dem physikalischen Blickwinkel)
Was ist eigentlich mit der Eigenschaft "normal"? Wir hatten im Skript den Spektralsatz für endl. dim:e HR:e auch für normale Operatoren angegeben (nicht selbstadjungierte) Macht sowas auch im unendlich Dimensionalen Sinn?
Im Voraus schonmal ein grooßes Dankeschön an diejenigen, die sich da durchackern und mir Rückmeldung geben. Liebe Grüße |
|
 |
mathilope
Anmeldungsdatum: 26.06.2015
Beiträge: 6
|
 mathilope Verfasst am: 29. Jun 2015 20:17 Titel: Die Fragen nochmal explizit mathilope Verfasst am: 29. Jun 2015 20:17 Titel: Die Fragen nochmal explizit |
 |
|
1. Kann  auch unendlich dimensional sein, wenn er eben kein unendliches ONS (bzw. später ONB) besitzt, sondern nur ein endliches? auch unendlich dimensional sein, wenn er eben kein unendliches ONS (bzw. später ONB) besitzt, sondern nur ein endliches?
Anm.: (mit später wollte ich nicht sagen, dass die ONS sich immer zu einer ONB erweitern lässt. Könnte man auch weglassen)
2. Und der [Anm.: der  ) ] ist ja auch physikalisch besonders relevant (lösungen des harmonischen Oszillators liegen ja z.B, darin, oder? ] ist ja auch physikalisch besonders relevant (lösungen des harmonischen Oszillators liegen ja z.B, darin, oder?
Anm.: Eh nicht so wichtig.
3. Reichen nun die separablen Hilberträume doch nicht aus, um die handelsüblichen Probleme der QM zu betrachten?
4. Da [Anm.: in der Parsevallschen Gl. ] ist dann schon eine Zerlegung der Identität bzgl. einer Basis enthalten [...] oder bin ich da zu voreilig, weil es eben nicht so leicht ist die Eins zu zerlegen? Bei einer ggb:en Basis stimmt das aber doch, oder?
5. Das [Anm.: stetig sein] ist nun nur noch zwangsläufig für Operatoren der Fall, die ebenfalls auf dem ganzen unendlich dim:en HR def. sind.
(bei dieser Aussage bin ich mir nicht sicher, die ist auch aus dem Skript. Gilt das vielleicht nur für symmetrische Operatoren? Also Def:bereich ganz H + symm. => stetig ? Die abgeschwächte Aussage ist aus der Wikipedia, auch hierzu habe ich eine Frage. Da wir uns in komplexen Hilberträumen bewegen, ist dann nicht eher hermite'sch statt symmetrisch gemeint? )
6. Und da wir ja letztlich häufig (immer? Oder gibt es auch andere interessante Fälle) auf Observablen hinauswollen, die durch selbstadjungierte (impliziert ein Adjungiertes) Operatoren dargestellt werden, ist das wichtig.
7. Jetzt habe ich auch hier direkt eine Frage: Ist die Gleichheit der Definitionsbereiche auch schon gleichbedeutend damit, dass A abgeschlossen ist?
8. Stimmt das [Anm.: das ganze Rumgefrickel mit Integralmaß und Intervallen und bla] so? Ich habe wirklich nicht viel Ahnung von Spektralmaßen, eigentlich weiß ich nicht genau, was hier Spektralmaß ist, was Träger, was Spektralschar und ob die Schreibweise des Integrals stimmt und sinnig ist, weiß ich auch nicht. Hier brauche ich wirklich Hilfe. Vielleicht hab ich's aber schon intuitiv richtig gemacht.
9. Wie schreibe ich das [Anm.: die Zerlegung eines HRs im Fall (ii) ]? Mit einem stetigen und nicht stetigen Kern und dem span vom ONS?
10. Dann gibt es ja noch weitere Sonderfälle von Operatoren, die werden aber hauptsächlich in der Mathe verwendet oder? Lohnt es sich überhaupt zwischen (allesamt selbstadjungierten) beschränkten, kompakten und allgemeinen Operatoren zu unterscheiden (aus dem physikalischen Blickwinkel)
11. Was ist eigentlich mit der Eigenschaft "normal"? Wir hatten im Skript den Spektralsatz für endl. dim:e HR:e auch für normale Operatoren angegeben (nicht selbstadjungierte) Macht sowas auch im unendlich Dimensionalen Sinn?
Anm.: Dann würde ich eine Definition eines solchen Spektralsatzes nachliefern zur Überprüfung.
12. Was ich dann ganz vergessen habe. Zu den Spektralsätzen hätte ich gerne Rückmeldung, ob das so passt.
Jetzt ist das ganze vielleicht besser geordnet und es kann leichter darauf geantwortet werden. |
|
 |
Jayk
Anmeldungsdatum: 22.08.2008
Beiträge: 1450
|
 Jayk Verfasst am: 29. Jun 2015 21:55 Titel: Jayk Verfasst am: 29. Jun 2015 21:55 Titel: |
 |
|
|
Schau mal in Quantum Theory for Mathematicians von Brian Hall. Da gibt es vier Kapitel zum Spektralsatz (ein Kapitel für das intuitive Verständnis, ein Kapitel über den Spektralsatz für beschränkte selbstadjungierte Operatoren, ein Kapitel für die Beweise, ein Kapitel über unbeschränkte selbstadjungierte Operatoren). Mathematical Methods in Quantum Mechanics von Gerald Teschl ist auch empfehlenswert, aber deutlich anspruchsvoller (macht alles von Anfang an für unbeschränkte Operatoren, setzt aber im Gegensatz zum Hall kein Wissen über Funktionalanalysis voraus, sondern enthält ein eigenes Kapitel über Hilbert- und Banachräume incl. Beweisen, wohingegen Hall nur in einem Anhang die Resultate angibt). |
|
 |
mathilope
Anmeldungsdatum: 26.06.2015
Beiträge: 6
|
 mathilope Verfasst am: 29. Jun 2015 22:47 Titel: Danke für so schnell mathilope Verfasst am: 29. Jun 2015 22:47 Titel: Danke für so schnell |
 |
|
Danke für die Literaturhinweise. Ich schließe also auf eine Antwort auf Frage 10. Ja es macht wohl Sinn, zwischen beschränkten und unbeschränkten Operatoren zu unterscheiden. Frage mich gerade, warum? Die Beschränkheit bzw. Stetigkeit von 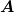 zu zu ^{-1} ) sollte sich eigentlich allgemein nicht vererben, oder? (Ich meine, das funktioniert schon im 1-D nicht immer) Naja, ich widme mich jetzt erstmal der Lektüre (sobald ich sie habe) bis dahin freue ich mich über weitere Rückmeldungen. sollte sich eigentlich allgemein nicht vererben, oder? (Ich meine, das funktioniert schon im 1-D nicht immer) Naja, ich widme mich jetzt erstmal der Lektüre (sobald ich sie habe) bis dahin freue ich mich über weitere Rückmeldungen.
Liebe Grüße |
|
 |
|
|















